基于增量式PID的步进电机速度控制系统设计*
许 洋,周 奎,杨亚会,杨 倩,向婧燕
(湖北汽车工业学院,湖北 十堰442002)
闭环控制系统设计是研究步进电机的关键技术之一,控制算法更是控制系统的重要组成部分。基于步进电机的控制系统设计,邱靖超等[1]提出了基于FPGA技术通过梯形加、减速算法实现了对步进电机的闭环控制;李娟等[2]使用单片机最小系统和驱动芯片实现了步进电机角度与转动方向的设计;谢海明[3]利用电脉冲信号控制相绕组电流,实现了步进电机的开环控制;王鹏宇等[4]提出了基于单片机和霍尔传感器来测量步进电机转速;朱嵘涛等[5]基于增量式PID算法实现了对直流电机的调速控制;控制系统设计中,一般会增设相关测速传感器来捕捉步进电机实时运动状态,但额外成本将随之增加,同时可能引入影响精度的其他不确定因素;考虑到设计的难易程度,相关学者通常采用开环或者应用常规PID算法,但电机运转精度将会受限;若应用模糊PID等算法,则需要实时权值优化,会加大核心硬件设备的运算负荷。李亚文等[6]设计了一种位置式PID算法来控制四旋翼飞行器的飞行姿态,但此算法可能存在积分饱和现象,且运算量大及占用存储单元多,会影响采样精度,造成采样信号失损;同时大幅升速或突加负载也会造成电机丢步甚至堵转。随着对步进电机精度需求的日益提升,仅依赖步进电机自身或采用传统如位置式PID控制算法已无法更好地满足工程技术要求。因此,亟需一类经济、低功耗且算法轻量级的步进电机控制系统。文中基于MCS51和增量式PID控制算法,设计实现了步进电机无极调速闭环控制系统。
1 控制系统架构
系统硬件由单片机、步进电机驱动器、步进电机、液晶显示屏、独立按键以及测速反馈模块构成。主控制器中的增量式PID算法程序将扫描到的键盘指令生成相应的数值作为定时器0的初值,同时定时器0通过中断和取反I/O端口来模拟产生占空比为50%的PWM波,并通过修改初值来调节频率的快慢,以达到目标转速。定时器1主要用作定时功能,同时通过中断来获得1 s内外部中断产生的次数,标志位为1;测速反馈模块和单片机的外部中断0端口相连来计算反馈电机的当前实际转速。系统的具体结构框图如图1所示。
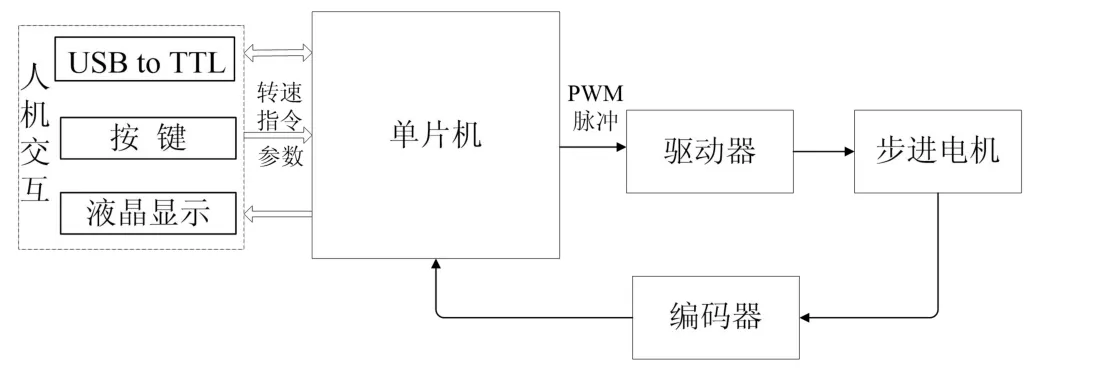
图1 系统整体结构框图
2 步进电机增量式PID算法
2.1 步进电机增量式PID控制
增量式PID算法是一种递推算法,其适用于自身带有积分记忆元件的执行器,其输出值是控制量的增量,并非执行机构的实际动作位置,即执行器的动作位置与输入信号不呈对应的关系,因此设计中选用增量式PID控制算法。
微控制器根据编码器通过采样计数获得的脉冲信号解算得到步进电机的实际转速,并将此转速度值传递给增量式PID控制程序,以此输出第i次采样时刻的控制量的增量∆ui,此值用于修正定时器比较值,进而控制器将输出相应高低频率的PWM脉冲信号来实现对步进电机转速的闭环控制,增量式PID控制系统框图如图2所示。图中:r(t)为设定的目标转速,y(t)为系统实际测量值,e(t)为设定值与实际测量值的误差。
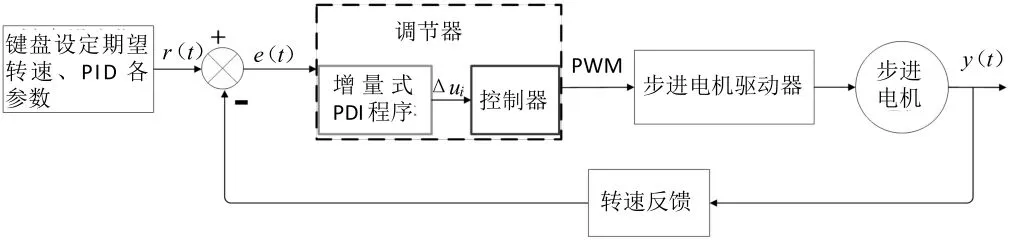
图2 增量式PID控制系统框图
数字PID微机测控系统是离散时间系统,故需对模拟PID调节器进行离散化处理,此时采用差分方程来描述此算法模型,即用后向差分表示微分、通过数值逼近法用求和代替积分。将偏差e(t)的P、I、D的参数通过线性组合来构成PID数字控制系统,模拟PID算法表达式为:

式(1)中:u(t)为PID调节器输出;e(t)为PID调节器偏差,即转速误差。
经过拉式变换可得控制器的传递函数表达式为:

将模拟PID控制算法离散化可得:

式(3)中:T为采样周期;i为控制周期采样序列。即:

由式(1)和式(4)可得,第i时刻采样时间的输出值u(i)与之前各采样时刻状态均有关,此算法需对采样数据的偏差e(i)累加求和,计算量大,占用控制器存储单元多。而且当系统控制量已达到极限值时,若误差依旧在积分作用下持续累加,将会产生积分饱和现象,造成系统大幅度超调甚至失稳。
对式(4)进行优化,假定系统输出控制量的增量为∆ui。由式(3)可得控制器在第i-1时刻的输出值为:

由u(i)=∆u(i)+u(i-1)可得增量式的PID控制算法的表达式为:

由式(6)可知,增量式PID算法采用加权处理,不需对e(j)累加,只需确定最近3次测量值偏差,就可得出控制增量∆ui,控制器运算负荷小,同时计算误差很小,对执行机构影响较小。
2.2 步进电机数学模型建立
为更好地实现对步进电机的运动控制,现由电气与机械两个部分建立数学模型,设计选用的电机型号为HK42BYG250-001,精度为步进角的3%~5%,主要电气参数如表1所示。
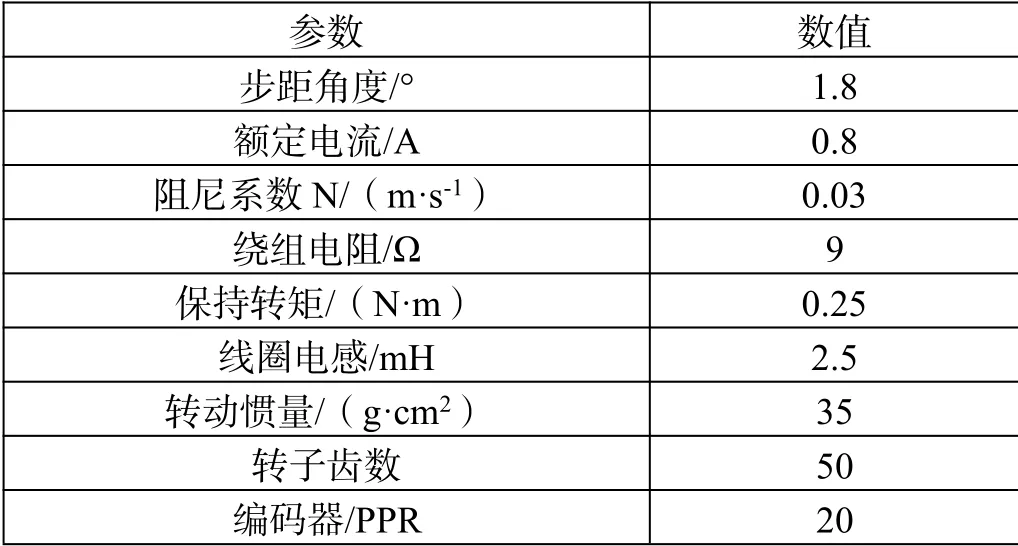
表1 步进电机主要电气参数
假设电气部分磁路不饱和且线性化,即可等效为具有混合式步进电机拓扑特性电路;机械部分由阻尼系数和惯性力矩的状态矢量模型描述。
两相混合式步进电机模型如图3所示,不同的研究对象,可以得出不同的传递函数[7-8]。根据小振荡理论,当给步进电机输入脉冲信号使其执行相关动作时,假设期望的转速为vE但实际转速为vA,则可得步进电机输出与输入之间的传递函数为[9]:
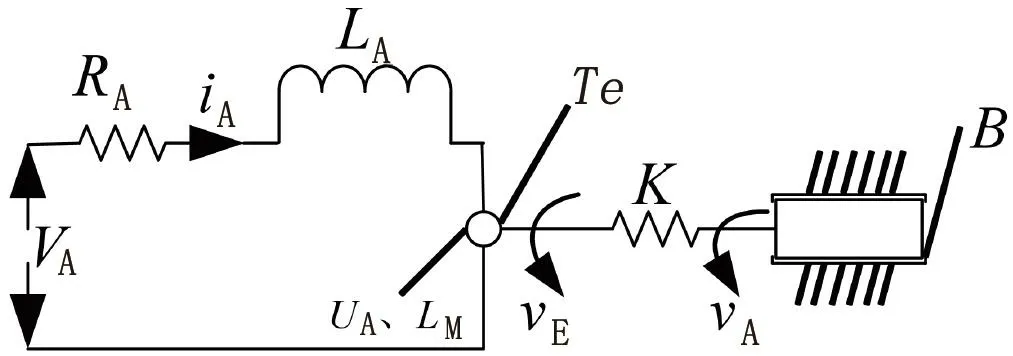
图3 步进电机数学模型

又因系统响应的时间无差别,则可得:
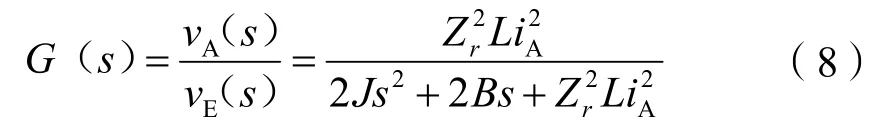
式(8)中:Zr为转子齿数;L为相电感;iA为电机A相电流;J为转动惯量;B为制动阻尼常量。
因此,可得步进电机速度传递函数为:
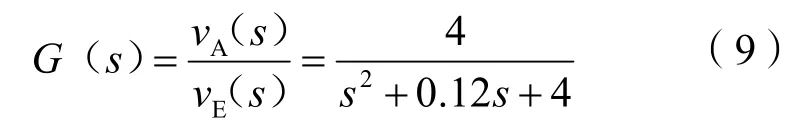
CPU内部结构中,算术逻辑运算单元ALU(8位)用来进行四则算术运算、逻辑运算以及循环移位和位处理;寄存器阵列中工作寄存器R0~R7(8位)用以暂存运算数据和中间结果,同时ALU处理的数据和计算结果需要经过累加器Acc(8位)进行累加,且寄存器B(8位)会与Acc配合来执行乘、除运算;而且MCS51指令周期为一个机器周期,MUL(乘法)和DIV(除法)运算的指令执行时间需要4个机器指令周期,又因为式(1)和式(4)中数据传送以及算术运算类指令条数较多,占用的机器周期相对较多,MCU对指令的执行总时间也将延长,不利于精确采样,影响系统控制精度。
微处理器的数据存储器极限容量为64 K,外部事件计数最大值为65 536次,由式(1)和式(4)可知此时需将之前各采样时刻误差值进行累加和存储,数据冗杂,占用空间很大,势必会对采样精度和系统灵敏度造成影响;而式(6)仅需近3次时刻采样误差值,输出的仅为加权处理后的第i采样时刻的控制量的增量∆ui,因此输入到式(9)中的数据值较小且位数更低,更利于微处理器的运算。
3 实验及仿真分析
为测试步进电机控制系统的可行性与动态性能,搭建了步进电机实验调试平台。控制系统电路由电源电路、MCS51单片机核心系统、TB6600驱动电路和LCD液晶显示电路等模块构成,电路原理图如图4所示,实验调试平台如图5所示。
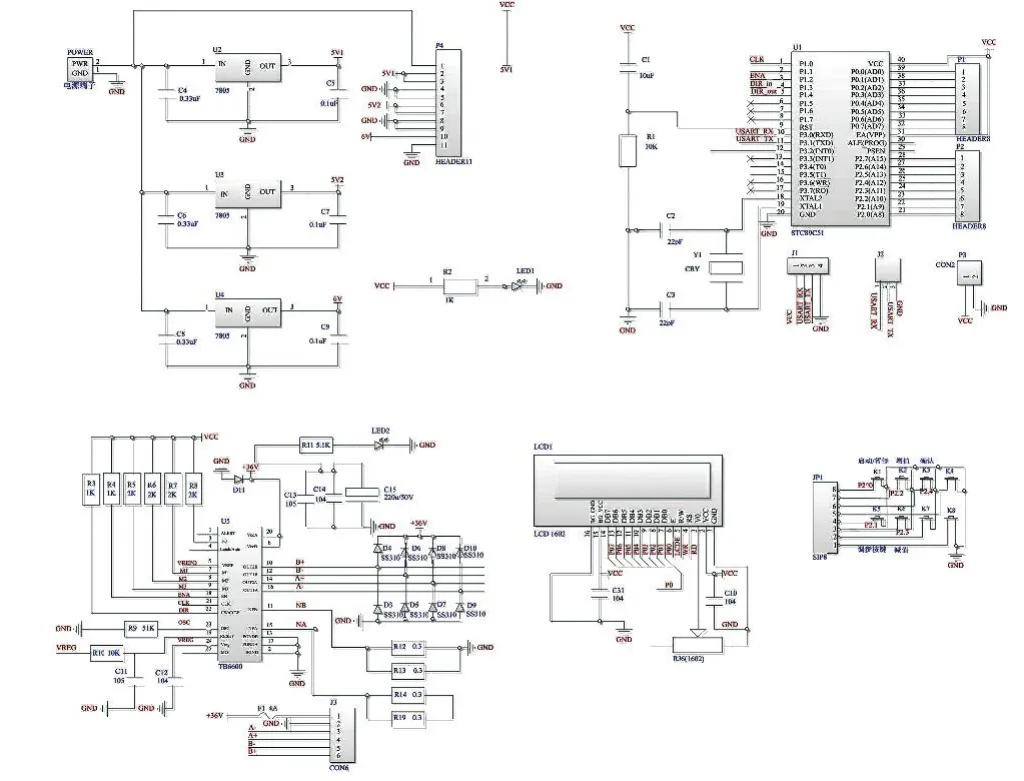
图4 控制器电路原理图

图5 实验调试平台
3.1 实验环境
实验平台设置由Windows10 i7-1065G7计算机、2020b版本MATLAB/SIMULINK模块等组成;微处理器MCS51通过Keil uVision5软件,采用C语言进行程序的设计与编写。
3.2 控制系统仿真分析
在MATLAB/SIMULINK环境中对增量式PID控制器的有效性和工作性能进行仿真。根据前述推导的传递函数模型,分别采用普通PID控制器和增量式PID控制器对定时器0模拟输出的PWM方波脉冲进行跟踪控制仿真,结果如图6和图7所示。
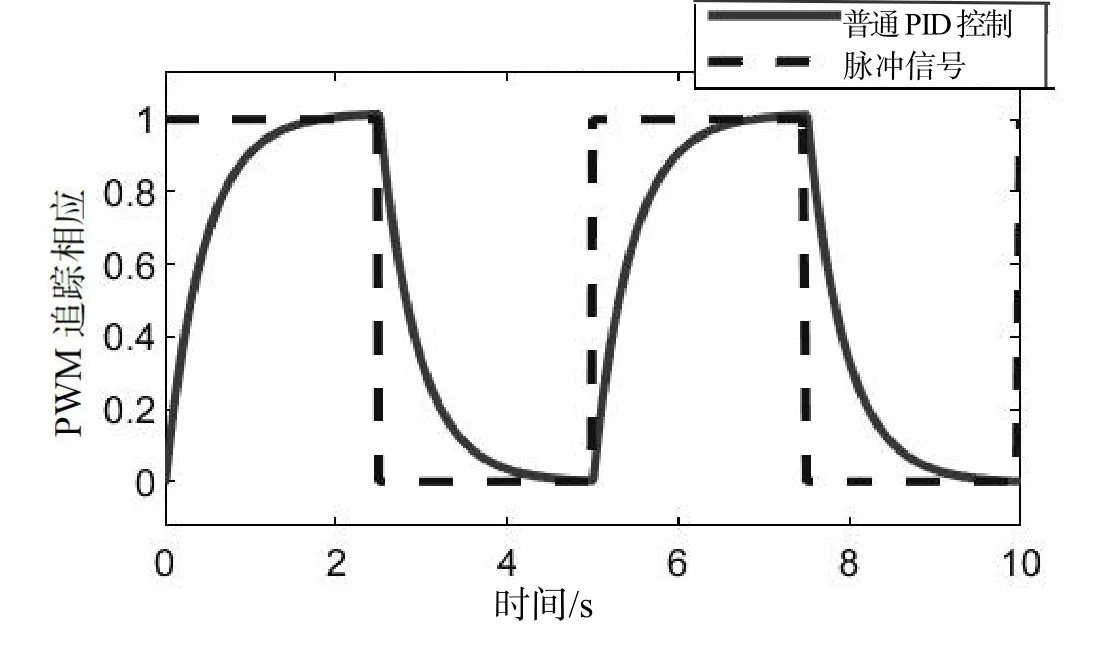
图6 普通PID控制的方波脉冲追踪响应曲线

图7 增量式PID控制的方波脉冲追踪响应曲线
由图6和图7对比分析可知:图6中普通PID控制器对输出信号的方波脉冲跟随性不理想,响应速度相对较慢,动态性能及精度尚待提升;图7中采用增量式PID控制器进行的脉冲追踪响应曲线则具有明显优势,响应时间缩短,响应速度得到提升,同时动态响应过程中信号的跟踪性能好,几乎可以复现PWM方波样本信号。仿真结果表明增量式PID控制器具有更好的动态响应性能,具备更好的适应性和鲁棒性。
对步进电机的快速响应能力和抗干扰性能进行仿真分析。输入期望转速信号为顺时针190 r/min,电机空载开始启动。普通PID控制和增量式PID控制的转速响应的曲线分别如图8和图9所示,其动态性能如表2所示。由仿真实验可得,与传统PID控制器相比,增量式PID控制器对步进电机转速控制具有更快的响应速度、更小的超调量以及更高的控制精度。

图8 普通PID控制步进电机的速度阶跃响应曲线

图9 增量式PID控制步进电机的速度阶跃响应曲线

表2 两种控制方式下空载快速启动实验性能对比
系统突加负载扰动实验,实验中输入期望转速信号为顺时针190 r/min,在步进电机稳定运行到3 s时,突加负载进行扰动,7 s时立即撤去此负载。图10和图11为实验所得的波形图,其中图10是普通PID控制器对负载扰动的响应结果,图11是增量式PID控制器对负载扰动的响应情况。
通过比对分析图10和图11中两种控制器对负载扰动工况的响应曲线,经过总结可得到其性能对比情况如表3所示。

图10 普通PID控制对负载扰动的响应曲线

图11 增量式PID控制对负载扰动的响应曲线

表3 两种控制器对负载扰动响应实验性能对比
由上表可得,步进电机在突加负载工况时,普通PID控制方式下电机转速波动振幅为7.89%,而增量式PID控制器控制下的电机转速波动仅2.63%。实验表明,增量式PID控制器能够较好地抑制控制系统由负载的扰动而造成的转速波动;同时相比于普通PID控制器,在增量式PID控制器控制下的系统稳态调节过程也更迅速。在突撤负载工况实验中,结果保持一致。因此,增量式PID控制器对两相步进电机的控制具有更好的鲁棒性,应对一定负载摄动时的控制效果更佳。
4 结论
以两相混合式步进电机为研究对象,闭环控制步进电机的转速为研究内容,应用增量式PID控制器控制步进电机,提出了一种基于MCS51的控制系统设计方案。通过MATLAB仿真和实验,结果均表明,运用增量式PID控制算法的步进电机闭环控制系统具备响应速度快、抗干扰能力强、控制精度高、运行稳定等优点,同时经济性、交互性和直观性效果均良好,为进一步研究步进电机的闭环控制提供了可选的参考。文中选用的磁电编码器技术参数为20 PPR,对控制系统稳态调节时间造成了一些延时,下一步将更换分辨率更高的编码器进行试验;同时文中采用的控制算法需要在应用场景中考虑输出限幅,尚存有一定的局限性,下一步计划将STM32等作为控制核心。

