基于模糊控制理论的PID闭环控制系统的研究与设计

李强

摘 要： 为了满足各种复杂控制任务，适应市场环境的千变万化，快速、准确及优质地完成各种工业控制要求，研究设计了一套基于模糊控制理论的PID闭环控制系统。系统设计以PID算法原理为基础，以数字化为实现方法，运用模糊控制理论，并实现控制系统的参数自整定。研究搭建相应的RC一阶电路硬件调试平台，通过相关软件设计，完成PID闭环控制器的调试，实现基于模糊控制理论的PID控制系统的相关功能，试验过程中使用高精度的AD/DA转换器确保系统的数字化精度要求，足以提升系统的适用性和有效性。实验表明，基于模糊控制理论的PID闭环控制系统能满足各种工业控制要求，具有较强的现实意义。

关键词： 自动控制； PID控制； 模糊控制； 参数整定； RC一阶电路； 闭环控制

中图分类号： TN911?34 文献标识码： A 文章编号： 1004?373X（2015）22?0131?04

0 引 言

随着科学技术的快速发展，最早以解决生产实践问题建立的工程控制理论在科学技术领域飞速发展，控制理论对生产力的发展、尖端技术的研究、尖端武器的研制及对非工程系统包括社会管理等方面均产生了重大的影响。因此，控制理论在它建立后的短时期内便迅速渗透到许多科学技术领域中。

各种工业技术高速发展的今天，工业自动化水平也日益提高。但在生产过程中，产品的质量受多因素的干扰而使自动化水平的优点逊色，包括PID控制理论在内的相关控制理论从此应运而生。目前，PID控制器已广泛应用于化工、冶金、机械、热工和轻工等领域，特别用于具有典型动态特性的温度、压力、液位、流量等工艺参数的控制，可达到良好的控制效果。目前大多数工业控制器都是PID控制器或其改进型控制器。尽管各种新型控制器不断出现在控制领域，但由于PID控制算法的各种优点，如原理简单、使用方便、适应性强及鲁棒性强等，PID控制器仍处于主导地位。随着 PID控制器的不断应用及发展，其改进型的控制器也在不断出现，相应的控制理论也得到了不断完善，结合 MCU和PC的智能控制也大量采用 PID算法，特别是对于复杂系统应用较为广泛的模糊PID控制器。

针对越来越复杂的控制现场以及越来越高的工业控制要求，提出了一套新型的PID闭环控制系统。该系统设计基于PID算法原理及数字化实现方法，结合模糊控制理论，并采用参数自整定原理实现。研究搭建相应的RC一阶电路硬件调试平台，通过相关软件设计，完成PID闭环控制器的调试，实现基于模糊控制理论的PID控制系统的相关功能，系统采用高精度A/D及D/A保证系统数字化精度要求，实现控制系统的有效性。实验表明，该控制系统均能满足各种控制要求，具有很强的现实意义。

1 系统总体设计

系统总体框图如图1所示，系统以PID控制器为核心，根据控制对象确定控制目标，通过相关研究及评价，结合模糊控制理论，完成系统的PID闭环控制过程。

1.1 PID控制器

参数自整定模糊控制是以先验知识和专家经验为控制规则的智能控制技术，可以模拟人的推理和决策过程，因此无须知道被控对象的数学模型就可以实现较好的控制，且响应时间短，可以保持较小的超调量。鉴于本系统设计要求在于对 PID算法及参数的整定分析，使系统达到较好的控制效果，因此系统 PID算法实现选择基本PID控制器，以实现PID算法的数字化。PID控制是经典控制理论中最典型的控制方法，对工业生产过程的线性定常系统，大多采用经典控制方法，它结构简单，可靠性强，容易实现，并且可以消除稳定误差，在大多数情况下能够满足性能要求，其结构图如图2所示。

PID控制器根据给定值r（t）与实际输出反馈值y（t）构成控制偏差，即：

[e（t）=r（t）-y（t）]

其控制规律为：

[u（t）=KPe（t）+TI01e（τ）+TDde（t）dt]

式中：u（t）为控制器的输出信号；e（t）为控制器的偏差信号，它等于给定值与测量值之差；[KP]为控制器的比例系数；[TI]为控制器的积分时间；[TD]为控制器的微分时间。

1.2 模糊控制

模糊控制是模糊集合理论中的一个重要方面，是以模糊集合化、模糊语言变量和模糊逻辑推理为基础的一种计算机数字控制。模糊控制是一种非线性智能控制，它具有许多传统控制无法比拟的优点，其基本原理如图3所示。它不需用精确的公式来表示传递函数或状态方程，而是利用具有模糊性的语言控制规则来描述控制过程，因而它具有很大的灵活性，可以根据实际控制的对象修改基本的模糊控制器。控制规则通常是根据专家的经验得出的，所以模糊控制的基本思想就是从行为上模仿人的模糊推理和决策过程的一种智能控制方法。

模糊控制的核心部分为模糊控制器，控制规律由微机程序实现。其实现控制算法的过程描述如下：微机经过中断采样获取被控制量的精确值，然后将此量与给定值比较得到误差信号[E]，一般选误差信号[E]作为模糊控制器的一个输入量。把误差信号[E]的精确量进行模糊化变成模糊量。误差[E]的模糊量可用相应的模糊语言表示，得到误差[E]的模糊语言集合的一个子集[e]（[e]是一个模糊矢量），再由[e]和模糊控制规则（模糊算子）[R]根据推理的合成规则进行模糊决策，得到模糊控制量[u]。

由系统总体框图可以看出系统采用RC一阶电路验证控制系统的优越性。系统把误差[E]及其变化率[EC]作为输入语言变量，把控制量[U]作为输出变量。考虑到变量的正、负性对误差[E]、误差变化率[EC]和控制量[U]选用7个语言变量值即：{正大，正中，正小，零，负小，负中，负大}={PB，PM，PS，0，NS，NM，NB}。

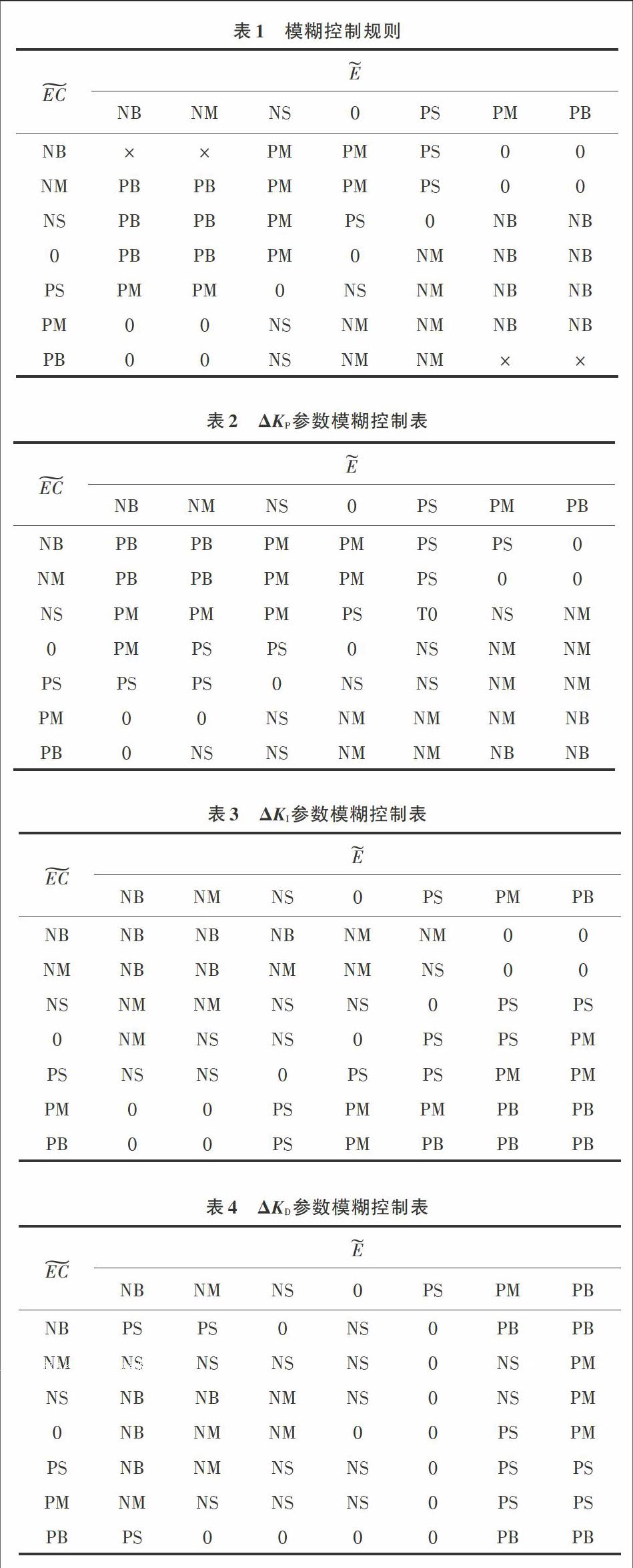
将上述模糊控制规则表1的模糊子集赋予相应的模糊数，则表1就变成了模糊数模型。该模型就相当于常规模糊控制器的模糊控制查询表。有了该查询表在后续进行控制中只需将模糊控制规则表中的模糊子集换成相应的模糊数，就可以得到所需的模糊数模型。这样修改模糊控制规则时就不需要进行推理运算，只需将表2中模糊子集换成相应的模糊数模型，就能获得合适的模糊数模型。根据表1可以得到 [KP]，[KI]，[KD]三个参数的模糊控制表，见表2～表4。

表中，NB，NM，NS，0，PS，PM，PB分别表示负大、负中、负小、零、正小、正中、正大。建立好控制规则后，建系统误差[E]和误差变化率[EC]变化范围定义为模糊集上的论域，[E，EC={-5，-4，-3，-2，-1，0，1，2，3，4，5}]。其模糊子集为[E，EC={NB，NM，NS，0，PS，PM，PB}]。这样控制系统可以通过模糊逻辑规则进行模糊推理、查表，从而得到 PID算法的3个参数，进而调节控制量的输出。

模糊 PID控制器与常规PID控制器相比，它大大提高了系统抗外部干扰和适应内部参数变化的鲁棒性，减小了超调，改善了动态特性。与简单的模糊控制相比，它减小了稳态误差，提高了平衡点的稳定度。为了满足在不同偏差[E]和偏差变化率[EC]对 PID参数自整定的要求，利用模糊控制规则对 PID参数进行在线修改，便构成了参数模糊自整定的PID控制器。其实现思想是先找出 PID的3个参数与偏差、[E]偏差变化率[EC]之间的模糊关系，在运行中通过不断检测[E]和[EC]，再根据模糊控制原理来对 3个参数进行在线修改，以满足在不同的[E]和[EC]时对控制参数的不同要求，使被控对象具有良好的动、静态性能，而且计算量小，易于用单片机计算。图4为参数自整定的模糊PID控制系统框图。

PID控制系统框图现在令积分系数[KI=KPTTI]，微分系数[KD=KPTDT]，在不同的[E]和 [EC]下被控[TI]过程对参数[KP]，[KI]，[KD]的自整定可根据以下规律进行：

（1） 当[E]较大时，应取较大的[KP]和较小的[KD]（以使系统响应加快）且使[KI=0]（为避免较大的超调，因此去掉积分作用）。

（2） 当[E]中等时，应取较小的[KP]（使系统响应具有较小的超调），适当的[KI=0]和[KD]（特别是[KD]的取值对系统的响应影响较大时）。

（3） 当[E]较小时，应取较大的[KP]和[KI]（以使系统能有较好的稳态性能），[KD]的取值要适当，以避免在平衡点附近出现振荡。

根据图4参数自整定模糊PID控制器系统框图所示，得到模糊控制软件设计的流程图，如图5所示，系统将采集的返馈量[y（k）]与给定值[r（k）]做比较，得到误差[e（k）]，进一步计算出误差变化率[ec（k）]，得到误差[e（k）]及误差变化率[ec（k）]后，根据之前建立的一套模糊控制规则，对其进行模糊推理、计算从而得到系统调节所需要的 PID参数[KP]，[KI]，[KD]。这样根据模糊推理整定后的PID参数，PID控制器计算出控制输出量。当然模糊规则的建立是根据之前对实际系统测量数据的分析，考虑到各种因素所得到的，此过程是非常繁琐和复杂的工作。因此必须对被控系统做出大量的观测、数据采集之后，采用合理的模糊推理方法才能得到比较好的模糊控制效果，从而对之前 PID控制系统的控制效果进一步提高。

2 系统试验

系统实验被控对象为RC一阶电路，设计选用参数电容C为47 μF的电解电容，电阻R选择1 MΩ的金属膜电阻。控制电压由D/A输出，进入控制被控RC电路，反馈信号从电容上提取，送到A/D，此电压信号经程序PID算法之后得到控制量，随之再进入RC被控电路，这样达到闭环控制的效果。实际的RC一阶电路较复杂，传递函数受到外界环境的影响，电阻的阻值及电容的容值存在一定的变换。同时由于电阻及电容自身的精度问题，其阻值、容值也存在一定的误差。因此，准确的数学模型的建立比较困难。系统实验是在假设的理想条件下进行的，设计是通过对电容的充放电来实现PID算法的控制。假设电容最初的电荷量为0，即电容电压为0。在软件实现PID算法时，设定初始电压[u（0）]，然后通过D/A控制输出电压对电容进行充放电，A/D对电容电压采样后经软件PID 算法处理后调节D/A的控制电压输出，如此循环，此过程中可以看到电容上电压的一个波动过程，为了更好地调节PID的参数，把对电容电压的采样信号通过单片机的串口端送到PC机，进行数据分析，然后调节PID系数及采样周期。最后让电容电压稳定在预设电压[u（0）]。从而到达PID算法闭环控制的目的。

根据系统单片机采样被控系统RC一阶电路电容上电压返回电脑的数据，系统的控制效果见图6。在初始预设电压为2 V时，电阻阻值为1[MΩ]、电容容值为47[μF]、室温在27.5 ℃，参数[KP]，[KI]，[KD]分别取1.4，0.7，0.8时，可以达到较好的控制效果，第一个峰值为2.07 V，之后的第一个谷值为1.996 V。从串口传到电脑的数据来看两者之间包含14个采样数据，根据预设采样周期T=0.1 ms，及执行串口程序所需时间来看第一峰值与第一谷值之间时间在1.45 ms之间。

从传回的数据来看系统在电容初始电压为0 V时达到2 V预设电压时间在180 ms左右，当达到2 V预设电压后，基本稳定在1.988～2.002 V之间，没有出现大的波动与振荡，稳态误差在0.1%～0.6%。控制器各项指标均能满足系统要求，该设计对模糊控制器的应用具有很强的现实意义。系统控制效果如图6所示。

3 结 语

本文研究与设计了基于模糊控制理论的PID控制器，提出了较一种新颖的PID控制方法，应用参数自整定方法实现模糊PID控制器参数自整定。通过试验表明该模糊PID控制器各项指标均能满足设计要求，对现代工业控制领域具有较强的现实意义。

参考文献

[1] 王划一.自动控制原理[M].北京：国防工业出版社，2002.

[2] 黄友锐，曲立国.PID控制器参数整定与实现[M].北京：科学出版社，2010.

[3] 杨志忠.数字电子技术基础[M].北京：高等教育出版社，2004.

[4] 王建校，杨建国，宁改娣，等.51系列单片机及C51程序设计[M].北京：科学出版社，2002.

[5] LI Fangyuan， HAN Jinbao. FEM aided prestress design for large?scale ultra?low?temperature LNG tank [C]// Proceedings of the 3rd IEEE International Conference on Information and Computing. Wuxi， China： IEEE， 2010： 257?260.

（上接第134页）

[6] BARROSO L A， RUDNICK H， MOCARQUER S， et al. LNG in South America： the markets， the prices and the security of supply [C]// Proceedings of 2008 IEEE Power and Energy Society General Meeting： Conversion and Delivery of Electrical Energy in the 21st Century. Pittsburgh： IEEE， 2008： 1?6.

[7] CAO Wensheng. Natural gas liquefaction process for small?scale LNG project [C]// Proceedings of 2012 IEEE International Conference on Computer Distributed Control and Intelligent Enviromental Monitoring. [S.l.]： IEEE， 2012： 439?442.

[8] 施仁，刘文江，郑辑光.自动化仪表与过程控制[M].北京：电子工业出版社，2003.

[9] 王常力，罗安.分布式控制系统（DCS）设计与应用实例[M].北京：电子工业出版社，2010.