一种基于频率校正的BPSK信号高精度载频估计算法

易辉++侯孝民++吴涛

摘 要： 为了实现BPSK信号载频的高精度估计，提出一种基于频率校正的高精度BPSK信号载频估计算法。算法通过非线性变换将BPSK信号的载频估计问题转化为对点频信号的估计，再用DFT对点频信号进行粗估计，针对DFT估计频率分辨率差的问题，采用相位差校正法对DFT估计频率进行校正，从而实现BPSK信号载频的高精度估计。最后，通过性能分析和计算机仿真验证了算法的有效性，其结果表明：该算法在低信噪比情况下能获得较好的估计精度，在高信噪比情况下，估计精度大幅提高。

关键词： BPSK信号； 载频估计； DFT； 相位差校正法

中图分类号： TN914.2?34 文献标识码： A 文章编号： 1004?373X（2015）22?0004?04

载频估计是数字信号分析的重要内容。在测控任务中，通过测量飞行器和观测站之间的相对运动引起的载波多普勒频移可计算出飞行器的相对径向速度[1?3]。同时，在电子对抗中，尤其是对未知信号的侦查中，载频估计也是信号后续处理的基础[4]。因此，研究BPSK信号载频的高精度估计有着十分重要的意义。

BPSK载频估计的典型方法大致可分为两类：第一类是通过现代谱估计的方法进行谱估计及测频，这类方法算法复杂，计算量大，且需要较高的信噪比；第二类是通过对信号进行平方运算，将BPSK信号载频估计问题转化为点频信号频率估计问题[5]。该方法在工程中较为常用，其载频估计精度取决于点频信号的估计精度。

对于点频信号的估计，常用的有时域法、频域法、最大似然法和特征子空间法。时域法主要包括过零检测法[6]和相位法[7]，适合在信噪比比较高的情况下使用，在信噪比较低时性能急剧下降；频域法主要包括直接法（周期图法）、Rife算法[8]、Quinn算法[9?10]及其他基于DFT的各种改进算法；这些方法可以用快速傅里叶算法（FFT）快速实现，在工程上应用广泛。直接采用DFT法估计频率时，存在很严重的栏栅效应[11]，估计精度取决于频率分辨率。而频谱分辨率取决于采样频率和采样点数（FFT点数），当采样频率一定时，想要获得高精度的估计就必须不断提高采样点数，这会造成运算时间过长。

1 基于频率校正的BPSK载频估计算法

为了克服栏栅效应，同时兼顾运算速度，本文提出一种基于频率校正的BPSK信号高精度载频估计算法。离散频谱相位差校正法[12]，利用DFT变换后谱线的相位信息对离散谱线进行校正，可对点频信号的频率进行高精度估计。本文将离散频谱相位差校正法应用到BPSK信号的载频估计中，通过对BPSK采样信号进行平方运算，得到二倍载波的单频分量[2f0]，对得到的信号进行DFT运算，并对频谱进行最大值搜索便可获得BPSK信号二倍载频的粗估计。在此基础上，利用相位差校正法对离散频谱进行校正，便可得到二倍载频[2f0]的高精度估计。为了避免在平方运算后的频率模糊，需要在平方运算前进行二倍内插并滤除镜像。算法的处理框图如图1所示。

3 频率校正法性能分析

本文先对BPSK进行平方运算，将BPSK信号载频估计转换成电频信号频率估计。用DFT变换对点频信号进行粗略估计，在DFT估计的基础上，用相位差校正法对粗估结果进行频率校正。

相对于直接DFT估计，频率校正法只增加了频率校正过程，并不会增加太多运算量。由于增加了频率校正过程，DFT粗估计的精度要求不需要太高，前期做DFT的点数也可以相对降低。假设采样点数为[N2]点，经过内插滤波后变为N点，平方运算需要进行N次实数乘法运算，DFT用FFT实现需要[N2]log2 N次复数乘法运算，到此便是使用直接DFT估计的运算量；增加频率校正过程，第二段信号可以只做第[k0]点的DFT而不必做N点的FFT，这里需要N-m次复数乘法运算，增加的运算量主要来自这N-m次复数乘法，这相对于[N2]log2 N来说非常的小。由于本文是在DFT估计的基础上做频率校正，对DFT的频率分辨率要求不用太高，所用的采样点不必太长，这可以减小DFT的运算量。直接DFT估计的精度取决于DFT的频率分辨率，即由采样频率和采样点数决定，估计精度为频率分辨率的一半。而相位差校正法理论上的误差是极小的，不存在分辨率的问题。因此，在相同运算量的情况下，相位差校正法载频估计的精度将远远高于直接DFT估计法。

关于N和m的取值问题，N作为DFT的点数，N越大，时间越长，频谱越窄，旁瓣效应就越小，但N过大会导致运算时间过长，所以，N的选取要在精度和运算速度上做一折中。为了使第二次N-m点做DFT的点数尽量长（频谱尽量窄），m应取较小的整数值[12]。

4 仿真结果及分析

下面对上述算法进行仿真实现。仿真条件：待估计BPSK信号的载频为59 kHz，采样频率300 kHz，取N=1 024的个采样点。信噪比从-5～5 dB以0.25 dB的间隔变化，对每个信噪比做1 000次蒙特卡洛仿真。这里所说的信噪比是调制后信号的功率比噪声功率。

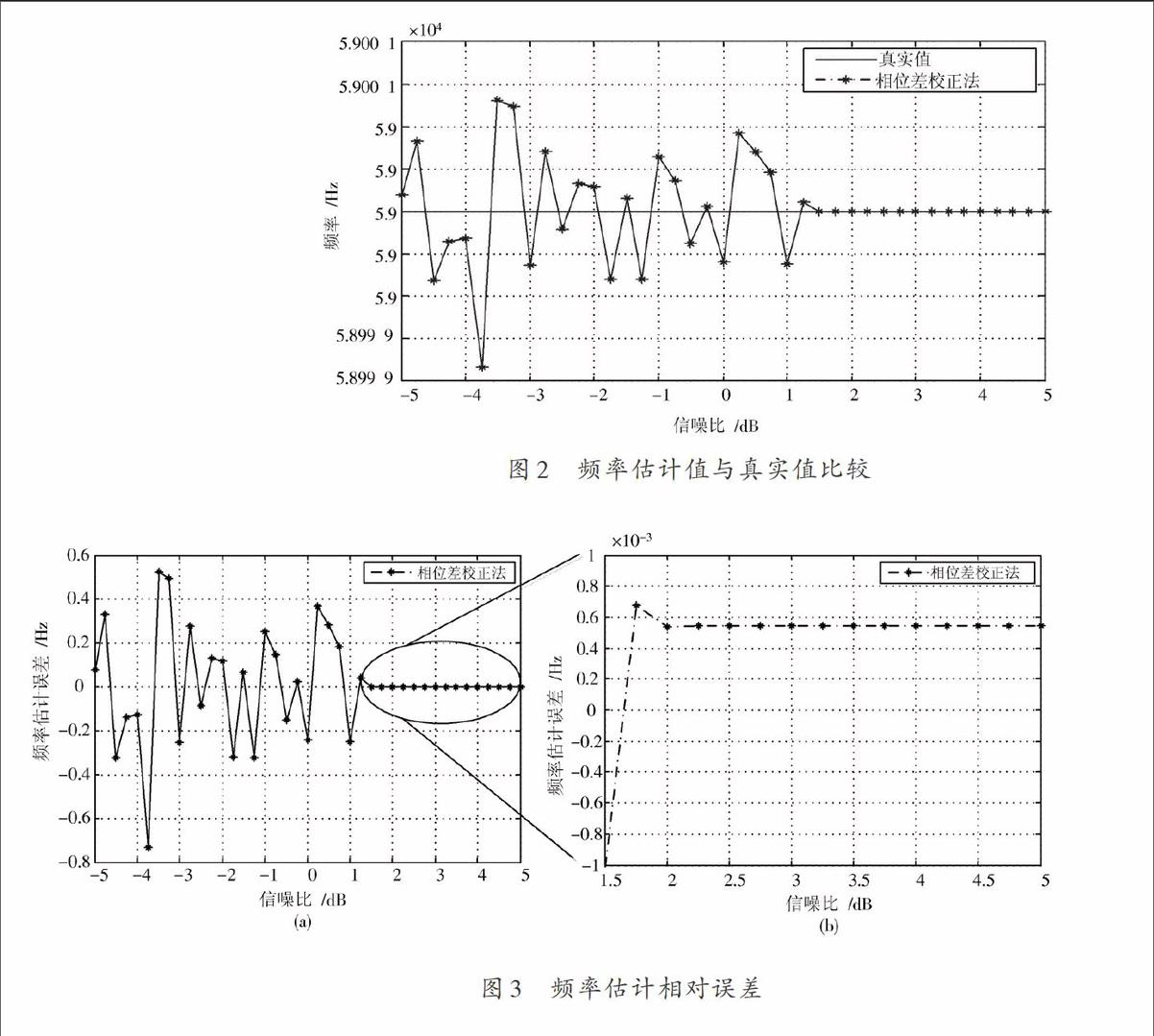
二倍内插并滤波后，信号点数将变为2 048个点，采样率变为600 kHz。如果只用FFT估计载频的话，此时频谱的频率分辨率为[Δf=0.293 kHz]，估计的精度为频率分辨率的一半，即[0.146 kHz]。若在FFT估计后，再做频率校正，估计精度将大大提高。1 000次蒙特卡洛仿真结果如图2，图3所示。

图2所示为载波频率估计值与真实值对比图。从图2中可以看出，当信噪比低于1 dB的时候，载频估计值在真实值附近上下大幅度波动。这是由于噪声过大，影响了相位差的计算结果，导致校正后，估计频率呈现出随机波动的现象。当信噪比高于1 dB时，估计频率逐渐稳定并趋近于真实值，在2 dB附近达到稳定状态。当信噪比高于2 dB时，载频估计值基本等于真实值。

图3所示为载频估计值减去真实值后得到的误差。从图3中可以看出，当信噪比低于1 dB时，估计误差较大且波动较为剧烈，但仍然远小于DFT的频率分辨率，估计误差在1 Hz以内。可以算出相对误差可达到[10-5]数量级。当信噪比高于2 dB时，估计误差在0.001 Hz以内，相对误差可达[10-8]数量级。

从图3中的放大图中还可以看出，当信噪比大于2.5 dB以后，频率估计的误差并没有再减小，而是一个稳定的值，这正是由于前面所分析的[XsN（ejω）]正、负频谱相互叠加所造成的。

5 结 语

本文将相位差校正法应用到BPSK信号的载频估计中，对算法原理进行推导并分析了算法的性能，通过仿真分析验证了算法的估计精度和有效性。基于频率校正的BPSK信号载频估计算法是针对DFT的频率估计的校正算法，具有速度快、实时性好的优点，有利于硬件实现。同时，该算法运算简单，估计精度高，可以有效克服栏栅效应，适用飞行器测控。

参考文献

[1] 刘嘉兴.飞行器测控与信息传输技术[M].北京：国防工业出版社，2011.

[2] 黄富彪，何兵哲.一种卫星信号载波频率精确估计算法[J].现代电子技术，2012，35（3）：129?131.

[3] 刘嘉兴.飞行器测控通信工程[M].北京：国防工业出版社， 2010.

[4] Richards Mark A.雷达信号处理基础[M].北京：电子工业出版社，2012.

[5] 郑纪民，胡亚.一种MPSK信号载频高精度实时估计算法[J].无线电工程，2012（5）：21?23.

[6] 张旻，王伦文，陈家松.用于通信对抗侦察的高精度测频方法[J].无线电通信技术，2000（5）：48?50.

[7] BOASHASH B. Estimating and interpreting the instantaneous frequency of a signal II： Algorithms and application [J]. Proceedings of the IEEE， 1992， 80（4）： 540?568.

[8] RIFE D R B. Single tone parameter estimation from discrete?time observations [J]. IEEE Transactions on Information Theory， 1974， 20（5）： 591?598.

[9] QUINN B G. Estimation of frequency， amplitude， and phase from the DFT of a time series [J]. IEEE Transactions on Signal Processing， 1997， 45（3）： 814?817.

[10] 谢胜，陈航，于平，等.基于Quinn算法和相位差法的正弦波频率估计综合算法[J].信号处理，2011（5）：771?775.

[11] 陈奎孚，焦群英，高小榕.提高 FFT 谱质量的一种新方法[J].振动·测试与诊断，1998（3）：62?66.

[12] 朱利民，贾民平，钟秉林.转子振动监测中的采样与相位误差补偿[J].东南大学学报，1997（2）：117?122.