基于Copula方法的甘蔗收入保险定价研究——以广西为例

王 悦 谈 娟 陈冰宇

（1.四川大学，四川 成都 610065；2.陕西省杨凌示范区科技创新和转化推广局，陕西 杨凌 712100；）

一、引言

食糖是关系国计民生的重要战略物资，糖业发展事关国家食糖安全。长期以来，我国政府高度重视糖料蔗生产，采取多项措施保障甘蔗生产，但由于农业本身具有弱质性，其生产过程中会面临自然与市场的多种风险。广西是中国最大的糖料蔗生产基地，但由于受自然灾害与国际蔗糖市场波动的影响，广西蔗农的生产积极性下降，对甘蔗生产与销售过程中开展风险管理具有重要意义。为分散农业风险、减少农业损失、保障蔗农收入，广西于1995 年推行甘蔗火灾保险，2008年开展甘蔗种植保险试点工作，2012年启动政策性糖料甘蔗种植保险试点，并于2016 年启动糖料蔗价格指数保险试点工作，2020年进一步推出“订单农业+保险+期货”模式的糖料蔗价格指数保险试点新方案。但以上传统产量保险只保障各种自然风险造成的损失，价格保险只保障市场风险造成的损失，都具有片面性。而农业收入保险既能承保自然灾害造成的损失，又承保市场价格波动造成的损失，具有防范产量与价格双重风险以及费率更低、更能发挥市场资源配置作用等优势。

尽管我国已连续六年提出试点与推广农业收入保险，但学术界目前还鲜有甘蔗收入保险相关研究。本文以广西为例开展甘蔗收入保险相关研究，具有重要的理论与现实意义。

二、文献综述

（一）国外文献综述

目前国外学者对农业收入保险的研究成果颇为丰富。

1.关于农业收入保险的研究。与传统农业保险相比，农业收入保险不仅价格较低，而且保障更全面（Goodwin，2015）。收入保险能够有效分散农业风险，因此农民往往会扩大生产规模、增加种植面积，同时投入更多生产资料和劳动力（You，2014），提高农业产出，推动农村经济发展。作为一类可持续的农业风险管理工具，农业收入保险已经成为政策性农业保险的发展目标（Mateos−Ronco &Izquierdo，2020）。

2.关于农业收入保险定价的研究。定价是所有保险产品的核心问题，农业收入保险也是如此。Coble et al.（2010）将收入保险的定价总结为四阶段：第一，分别计算单产和价格的边缘分布；第二，拟合单产与价格的联合分布；第三，基于前两步的结果随机模拟多组单产和价格数据；第四，计算不同保障水平下的纯费率。国内外收入保险定价时大都按照这四个步骤进行。

收入保险的定价以拟合产量和价格风险为前提，拟合分布的方法主要有参数法和非参数法两种。早期国外学者们多采用参数法进行估计，Botts &Boles（1958）假定作物单产服从正态分布后对其进行拟合，然而拟合效果不佳。随后，国外学者们使用单产和价格数据逐渐验证其他分布模型，主要包括Gamma、Beta、Weibull、Burr、Log−normal等。研究文献显示，国外学者多认为产量服从Beta 或Weibull 分布（Goodwin&Hungerford，2015）；价格服从Log−Logistic 和Log−normal 分布。近年来，参数法可能导致信息遗漏、拟合度不是最优等缺陷逐渐显现，非参数方法则可以弥补这些缺陷，逐渐成为当前收入保险定价的主流方法，其中应用最广泛的非参数方法是核密度函数法（Woodard et al.，2012）。

估计单产和价格的联合分布时，国外学术界最初普遍认为单产和价格风险相互独立，后来意识到单产与价格之间的负相关关系，学者们开始大量运用Copula 方法连接两种风险分布，以确定其联合分布。运用Copula方法定价时，Tejeda &Goodwin（2008）使用大豆和玉米的数据，对比Frank Copula 和Normal Copula 函数的各类系数，发现产量和价格呈负相关，且选取Frank Copula 函数时负相关关系更为显著；Ghosh et al.（2011）则提出了新的估计方法，即混合Copula方法，并以玉米的团体收入风险保险为例比较单一Copula估计和混合Copula的估计结果。

（二）国内文献综述

1.关于农业收入保险的研究。肖宇谷和王克（2013）认为，比起产量保险的片面性，收入保险可以全面保障风险，稳定农民收入。朱俊生和庹国柱（2016）提出，由于产量风险和价格风险会形成对冲，总体赔付风险随之降低，收入保险比产量保险和价格保险的费率更低。曾勤（2016）认为推行农业收入保险与供给侧改革的目标一致，同时可以避免政府对农产品价格的过度干预，有利于发挥市场在资源配置中的作用。帅婉璐和何蒲明（2017）持有相同的观点，提出在我国推广收入保险可以避免政府直接干预价格，有助于农产品价格机制改革。谷政和任志宇（2020）研究发现在同等保障水平下收入保险的费率要低于种植险，在同一费率水平下，农产品收入保险提供的保障高于现行的物化成本保险。殷铭阳等（2021）以辽宁省铁岭市为例，阐述收入保险为农户分散了农业生产中遇到的产量和价格两个核心风险，对玉米产量保险和收入保险进行纯费率计算，结果得出在同一保障水平下，玉米收入保险费率低于产量保险费率。

2.关于农业收入保险定价的研究。国内文献中对农业收入保险定价的步骤比较一致，即，第一，分别确定单产和价格的边缘分布；第二，选择合适的Copula 函数拟合单产与价格的联合分布；第三，用Monte Carlo模拟生成多组样本数据；第四，计算不同保障水平下的保险费率。具体研究方法上，大多数国内学者运用参数法确定价格和产量分布函数，少数运用非参数法；几乎所有学者都使用Copula方法确定联合分布函数。例如，谢凤杰等（2011）选取安徽省阜阳市的小麦、大豆、玉米单产和期货价格数据，运用参数法确定产量和价格分布函数，采用Copula函数确定联合分布函数，测算收入保险费率。赵玉（2019）则选取2004～2016年大中城市的番茄、黄瓜、菜椒和白菜等相关数据，采用非参数法和Copula 方法对蔬菜收入保险定价。谷政和任志宇（2020）选取1995～2016 年玉米主产地区玉米单产和现货价格数据，通过参数法拟合玉米单产和价格序列分布，采用Copula函数构建联合分布函数，由费率厘定公式计算出主要省份收入保险保费费率。研究对象上，很多学者都以我国不同地区、不同农作物为例探索收入保险的定价，但对象多为玉米、小麦、水稻和大豆等主要粮食作物，对经济作物的研究较少。

（三）文献述评与本文创新

纵观已有文献，学术界目前关于农业收入保险以及保险定价的研究较丰富，但鲜有关于甘蔗收入保险的相关研究。本文主要贡献在于选取广西甘蔗的产量和价格数据，运用非参数法分别确定其边缘分布，基于Copula方法拟合其联合分布，再用蒙特卡洛方法模拟出符合条件的数据，测算不同保障水平下甘蔗收入保险纯费率。在实施乡村振兴战略的背景下，本文对甘蔗收入保险的相关研究具有一定的理论与现实意义。

三、广西甘蔗收入保险费率厘定

（一）数据选取与研究方法

1.数据选取。选取1978～2018 年广西甘蔗单位面积产量（公斤/亩）数据，由总产量除以种植面积得到，数据来源于历年的《广西统计年鉴》；选取1978～2018 年广西甘蔗的平均出售价格（元/公斤），数据来源于《全国农产品成本收益资料汇编》。

2.Copula 理论。Copula 的概念由Sklar 在1959 年引入，即一个N维联合分布函数可以被分解成N个边缘分布函数和一个Copula函数。Copula是拉丁语，单词含义是“连接”，所以Copula 函数也叫作连接函数，Copula函数几乎包含了随机变量所有的相关关系，在估计变量相关性时被广泛使用。

Copula理论最初被用于概率度量空间领域，随着Copula 函数的更多特殊性质被发现，20 世纪90 年代后期Copula 理论开始在金融风险管理理论中得到发展和应用。后来，Copula 理论逐渐完善并迅速发展，其应用范围也越来越广，尤其是在确定随机变量之间的联合分布函数时起到重要作用。

N 元Copula 函数是指具有以下性质的函数（记为C）：

（1）定义域为［0，1］×［0，1］×…×［0，1］（共为N个域相乘）；

（2）C具有零基面且是N维递增的；

（3）C的边缘分布Cn，n=1，2，…，N，满足Cn（xn）=C（1，…，1，xn，1，…，1）=xn，其中xn∈［0，1］，n=1，2，…，N。

3.非参数核密度估计。设X1，X2，…，Xn是取自一元连续总体的样本，在任意点x处的总体密度函数f (x)的核密度估计定义如公式（1）所示。

其中，K()称为核函数，h称为窗宽。为了保证作为密度函数估计的合理性，要求核函数K()满足，即要求核函数是某个分布的密度函数。核函数有多种不同的表达形式，选取不同的核函数类型对核密度估计影响不大，因此一般选择应用最广泛的Gaussian核函数。

核密度估计中窗宽h的取值会影响到(x)的光滑程度，选择合适的窗宽是十分重要的，使用MISE函数求最合适的窗宽，求MISE的最小值点，可以得出最佳窗宽的估计值，其中f(x)是总体的真实分布密度，如公式（2）所示。

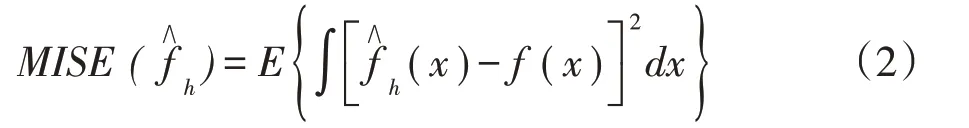
（二）拟合单产与价格的边缘分布

1.去趋势处理。对单产数据进行单位根检验得到结果：单产序列不平稳，因此，在进行分布拟合之前，需要对数据进行去趋势处理，采用Hodrick 和Prescott提出的HP滤波法对单产序列（X）进行去趋势处理。剔除时间趋势后再次检验单产序列的平稳性，结果显示单产序列在1%的显著性水平下平稳。

考虑到通货膨胀会导致价格序列出现明显的趋势，首先对价格（Y）数据进行去通胀处理，使用以1978年为基期的广西定基CPI对价格进行调整，目的是消除通货膨胀对价格的影响。经过去通胀处理后进行单位根检验，结果显示数据不平稳，因此再采用HP滤波法消除趋势影响。剔除时间趋势后再次检验价格序列的平稳性，结果显示在1%的显著性水平下平稳。

2.标准化处理。由于价格和产量数据的量纲不同，需要通过标准化处理消除指标之间的量纲和数量级差异的影响，即将数据按照比例进行缩放，使之落入一个特定的区域。选取常用的Min−Max 归一化法进行去量纲处理以消除单位的影响，如公式（3）所示。

经过标准化处理后，所有的数据均落在［0，1］范围内。

3.使用非参数法拟合边缘分布。为了确定单产和价格的分布类型，首先计算出峰度、偏度。单产序列（X）的分布是不对称的，偏度=0.12＞0，峰度=2.41＜3，与标准正态分布（偏度=0，峰度=3）相比右偏，凸起程度小于标准正态分布。价格序列（Y）的偏度=0.64＞0，峰度=3.38＞3，与标准正态分布（偏度=0，峰度=3）相比右偏，凸起程度大于标准正态分布。

根据单产和价格数据的偏度、峰度，并不能很准确地判断出其符合什么分布类型，因此需进一步深入研究。

由样本估计总体的分布，常用的估计方法有参数法和非参数法。参数法是事先假定服从某种已知分布，再估计参数，这种方法依赖于事先对总体分布的假设，要做出合理全面的分布假设存在较大难度，非参数法则不存在这样的问题，因此本文采用非参数法对数据进行拟合，当分布无法确定时，求样本经验分布函数，作为总体分布函数的近似值，或用核光滑方法估计总体的分布。为了避免参数法对分布形态的限制，更好地对产量和价格数据进行拟合，选择非参数估计中的核密度估计法。使用MATLAB R2018a软件进行计算分析，选取Gaussian核函数和相应的最佳窗宽进行核密度估计。

选择高斯核函数估计单产和价格波动序列的边缘密度函数，并且把核密度估计图、频率直方图和正态分布密度函数图放在一起进行比较分析。如图1、图2所示，单产和价格数据的核密度估计曲线均与频率直方图符合较好。

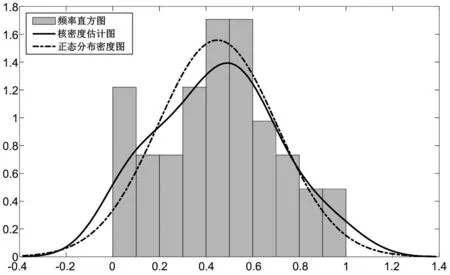
图1 单产序列的频率直方图、核密度估计图

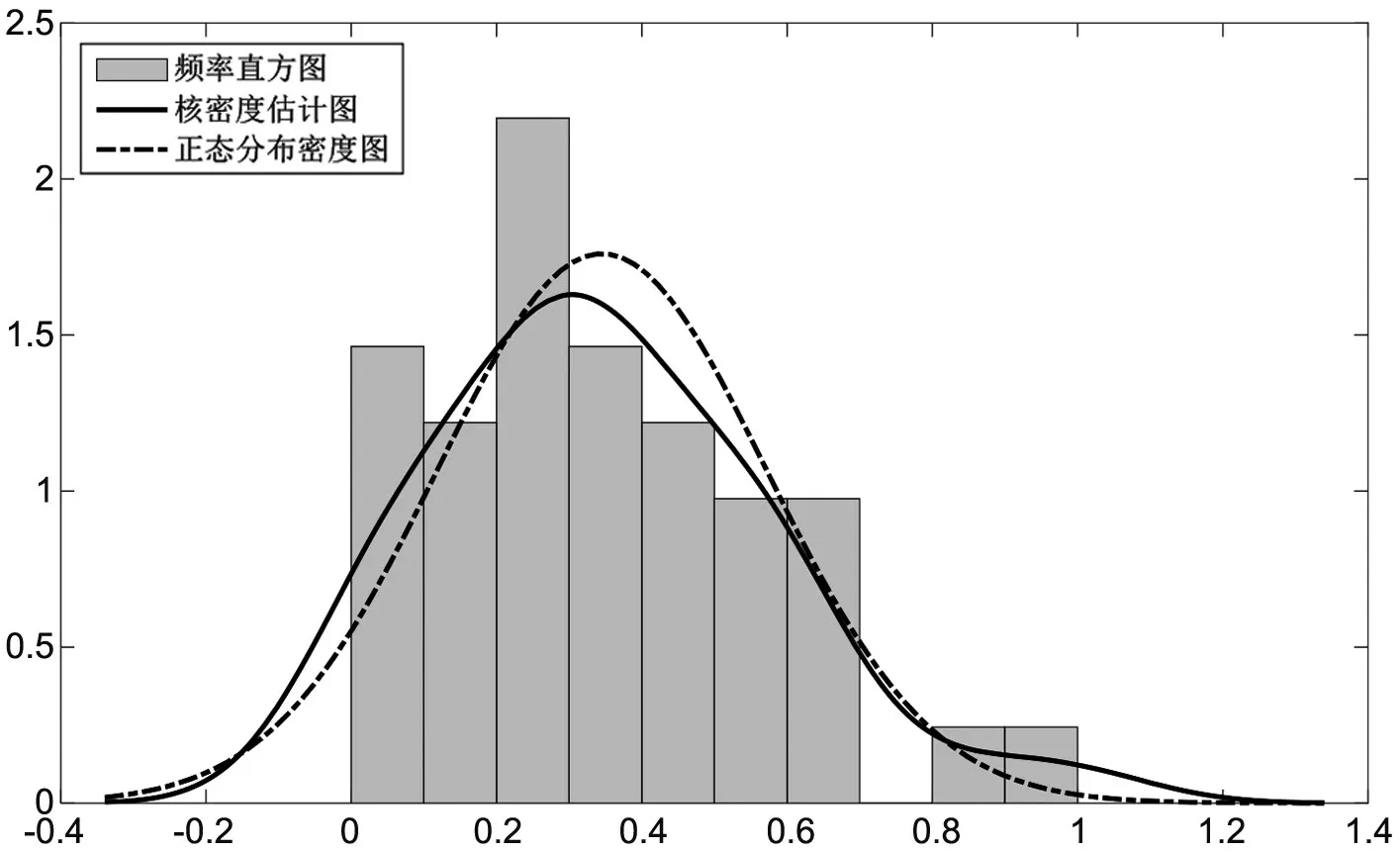
图2 价格序列的频率直方图、核密度估计图

将窗宽和其他测度值代入高斯核函数公式中就可以写出概率密度函数的表达式。

甘蔗单产的概率密度函数表达式如公式（4）所示。

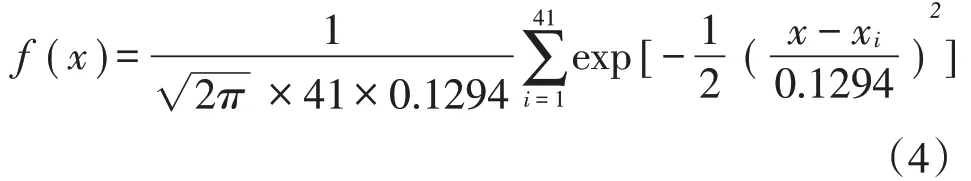
甘蔗价格的概率密度函数表达式如公式（5）所示。

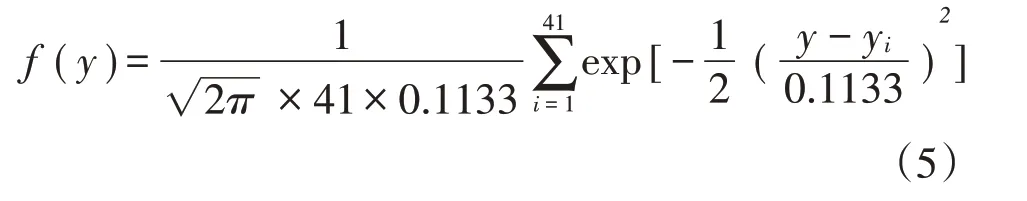
（三）确定单产与价格的联合分布

在确定单产和价格的边缘分布之后，就可以根据所选的Copula 与样本经验Copula 之间的平方欧式距离最短原则选取最适合的Copula 函数。选择最常见的Normal Copula（正 态Copula）、t−Copula、Clayton Copula、Frank Copula、Gumbel Copula 函数，分别计算参数、秩相关系数和与样本经验Copula的平方欧式距离，比较平方欧式距离，选择最合适的Copula函数。

引入经验Copula的概念。设(xi,yi)(i=1,2,…,n)是取自二维随机变量(X,Y)的样本，将X,Y的经验分布函数分别记为Fn(x)和Gn(y)，定义样本经验Copula如公式（6）所示。

u,v ∈[0,1]

其中，I[]为示性函数，当Fn(xi)≤u 时，I[Fn(xi)≤u]=1，否则I[Fn(xi)≤u]=0。

利用MATLAB R2018a中的copulafit 函数对单产序列和价格序列进行估计，并通过copulastat 函数计算各组Copula 函数的Kendall 秩相关系数τ 和Spearman秩相关系数ρ，最终结果如表1所示。

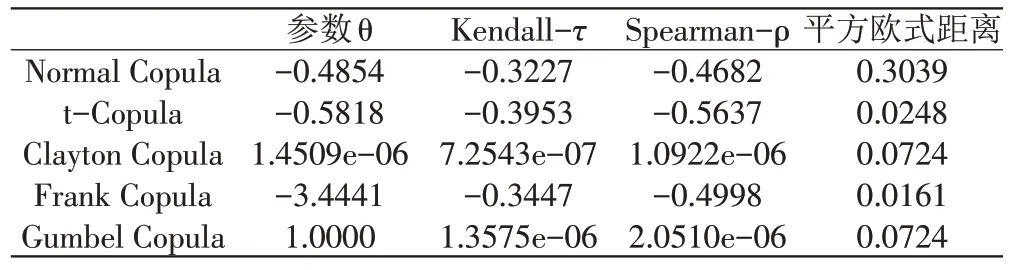
表1 Copula函数拟合结果

参数为−3.4441 的Frank Copula 与经验Copula 的平方欧式距离最小，对原序列的拟合效果更好，因此，应该选择Frank Copula 函数来连接单产与价格。从Frank Copula 函数的Kendall−τ 和Spearman−ρ秩相关系数来看，系数都为负，表示单产和价格之间存在负相关性。

（四）Monte Carlo模拟

上文虽然确定了单产和价格的Copula 联合分布形式及参数，但Copula 的密度函数形式比较复杂，难以直接写出其数学表达式，也难以直接进行费率厘定。因此，在已确定的单产和价格Frank Copula联合分布及其参数基础上，采用蒙特卡洛法模拟10000组单产和价格数据，算出单产和价格共同波动形成的收入序列。

具体步骤是：第一，基于选择的Frank Copula，调用copularnd 函数生成10000×2 的随机数矩阵，即10000组服从［0，1］上的均匀分布的随机数。

第二，根据前文得到的单产和价格的边缘分布，使用反函数法，计算与［0，1］分布随机序列相对应的函数值，如公式（7）所示。

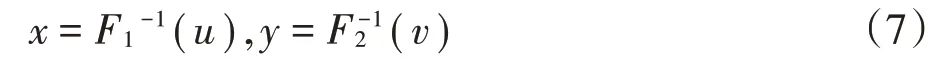
非参数核密度法估计得到的单产和价格分布函数的数学表达式十分复杂，难以直接求逆，因此借助样条插值法实现逆运算。

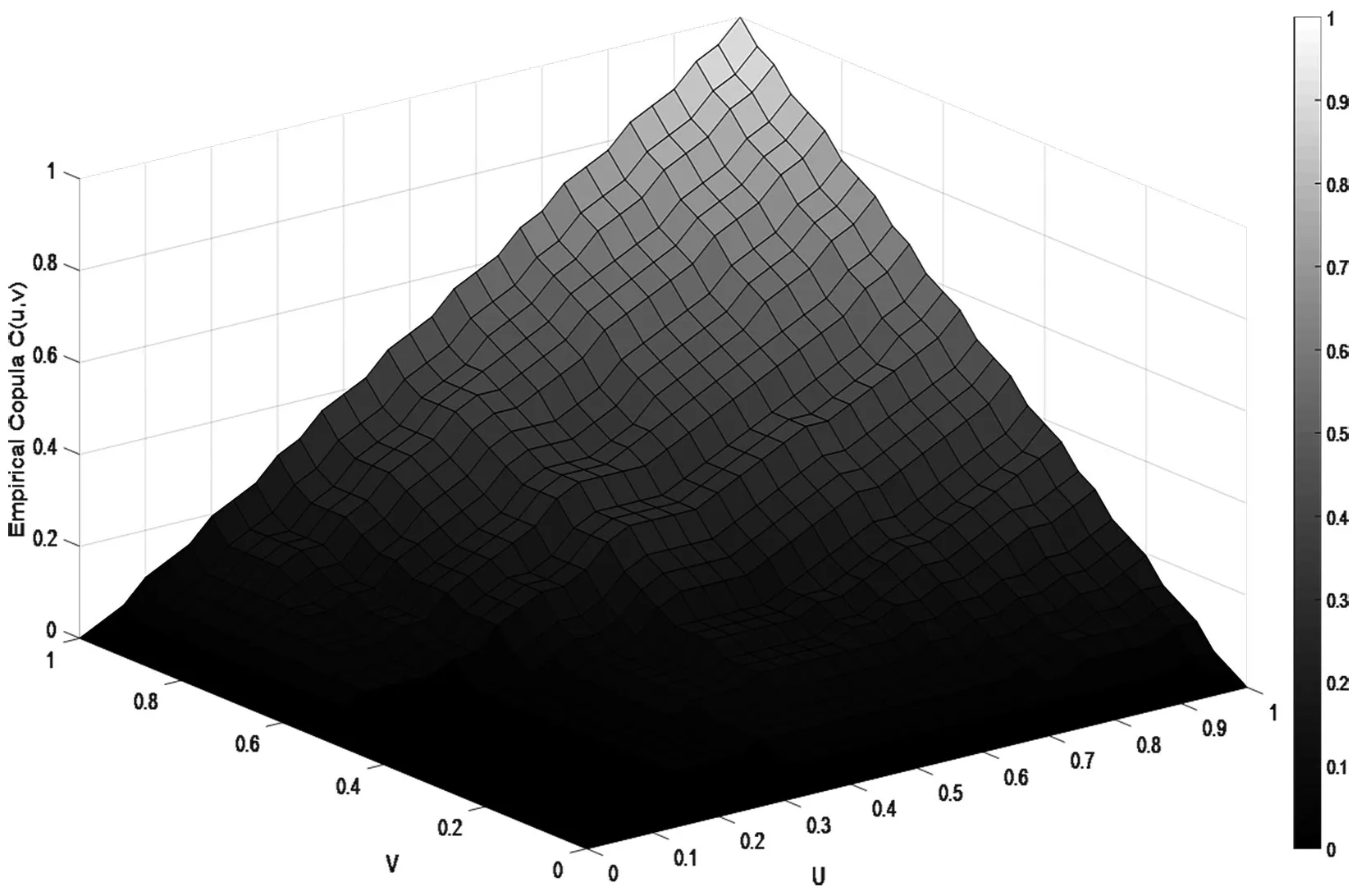
图3 经验Copula分布函数图

第三，将上一步得到的10000组数据按照之前的操作逆向还原，得到单产与价格数据，其乘积作为收入的样本值。

（五）计算甘蔗收入保险纯费率

使用Goodwin和Ker的精算公式，如公式（8）所示。

其中，A为甘蔗种植户的收入；为甘蔗种植户的期望收入；α为保障水平；ExpectedLoss(A)为甘蔗的实际收入低于预期收入的期望，即预期损失；r为纯保险费率。

计算得出不同保障水平下的收入保险纯费率如表2所示。

表2 不同保障水平下的纯保险费率

费率厘定结果显示，保障水平越高，保险费率越高，因此，甘蔗收入保险定价时首先要结合政策规定、地方财政状况以及农业保险发展现状，选择合理的保障水平。此外，最后得到的结果是纯费率，现实中保险公司定价时还要考虑到营业费用和利润空间。

（六）确定甘蔗收入保险保费

虽然已经计算出甘蔗收入保险的纯费率，但农民更关注的是实际保费，用保费表示也更具体、更直观，因此接下来将根据历史数据和纯费率计算出甘蔗收入保险的保费。计算公式如式（9）：

本文以平均成本加合理利润来确定保险金额。如表3 所示，选取近五年甘蔗的成本与成本利润率，分别求其平均值，根据式（10）计算得到结果：

表3 甘蔗的历史成本与利润率

保险金额=平均成本+合理利润

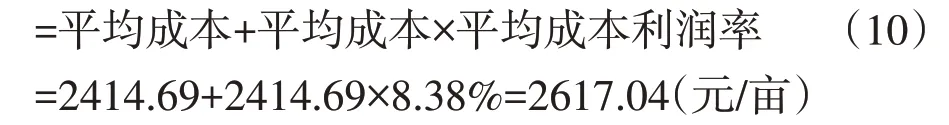
借鉴庹国柱和李军（2005）的计算方式如式（11）：

将前文计算出的纯费率代入式（11）中，结果如表4所示。

表4 不同保障水平下的收入保险毛费率和保费

选择合理的保障水平十分重要，为了避免加大逆向选择难度和道德风险，保障水平设置不宜过高，但保障水平太低又无法有效保障农业生产。参考2018年8月财政部、农业农村部、银保监会共同印发的《三大粮食作物完全成本保险和收入保险试点工作方案》中相关规定，保险金额应该低于农作物总收入的85%，故建议在推广前期将保障水平设置为70%，对应的甘蔗收入保险保费为142.6562元/亩。同时要逐步完善收入保险保障水平动态调整方案，初期可设置较低的保障水平，后期逐渐提高，保费也随之增加。

四、结论与建议

（一）结论

1.广西甘蔗单产风险和价格风险波动大。广西甘蔗生产规模大，易受干旱、暴雨洪涝、热带气旋（如台风）、高温天气和低温冷冻等各类自然灾害影响，一旦发生自然灾害，容易造成产量波动，甚至是巨大经济损失，农民收入缺乏保障。同时，受经济环境、市场竞争、供求变化等因素影响，广西甘蔗的市场价格波动幅度较大，存在较大的市场风险。

2.广西甘蔗产量和价格存在负相关关系。使用Frank Copula 函数拟合单产和价格的联合分布，其Kendall−τ 秩相关系数是−0.3447，Spearman−ρ 秩相关系数是−0.4998，表明单产和价格之间是负相关关系。收入保险通过产量和价格风险的对冲降低赔付风险，能实现比产量保险和价格保险更低的费率。

3.保障水平越高，收入保险纯费率越高。当保障水平为100%、90%、80%、70%、60%时，收入保险纯费率分别为11.80%、9.37%、7.26%、5.37%、4.50%。当费率过高时，农户负担不起高额保费，于是参保率降低；当费率太低时，保险公司保费收入低，可能发生较大亏损，降低保险公司开展业务积极性。因此，要综合考虑农民和保险公司的利益，选择一个最合适的风险保障水平，确定合理的保险费率。

（二）建议

1.加快开展收入保险试点工作。目前市场上的农业收入保险产品较少，仍处于小范围试点阶段，且试点品种为玉米、水稻等主粮作物。广西还未开展农业收入保险试点工作，相比较传统产量保险和价格指数保险，收入保险具有保障风险更全面、费率更低、更符合WTO 政策规定、更能充分发挥市场资源配置作用等优势。因此，建议尽快试点推广甘蔗等经济作物收入保险。

2.设定差异化风险保障水平。研究结果表明，风险保障水平越高，收入保险纯费率越高。当费率过高时，种植户负担较大；当费率过低时，保险公司保费收入低，可能发生较大亏损，因此，要同时考虑农民和保险公司的利益，选择一个最合适的风险保障水平。

3.设定合理的政府保费补贴比例。我国的农业保险具有政策性特征，即由各级政府承担一定比例的保费，减轻农民经济负担。根据保险标的、保险费率等的不同，确定合理的中央、省、市、县各级财政补贴比例，提高农户的风险意识和参保意识，提高参保比例。