基于多目标优化的圆锥动静压轴承特性分析*

郭 红 蒋雪晴 张泽斌

(郑州大学机械与动力工程学院 河南郑州 450001)

圆锥动静压轴承能够同时承受径向力和轴向力，且相对于向心轴承和平面推力轴承的组合，具有结构紧凑、稳定性好及易于调整等优点，在高速精密转子系统中应用越来越广泛。但高速圆锥轴承存在摩擦功耗高、油膜温升剧烈等问题，设计阶段需要特别注意。方晓丽等[1]用有限元法计算了具有深浅腔的圆锥动静压轴承静动特性，并验证了这种轴承形式具有良好的工作稳定性。RANA等[2]在不同的半锥角下，采用有限元和伽辽金方法，在迭代中应用适当的边界条件，求解了雷诺方程。GORASSO[3]运用遗传算法和人工蜂群算法，对轴承进行多目标优化，大大降低了轴承流量和功耗。岑少起等[4-5]建立了有限元-优化迭代的计算模型，以承载力最大作为优化目标，对浅腔深度、面积、封油边尺寸进行了优化计算，取得了较好的效果。刘建中等[6]用三维的方法研究圆锥动静压轴承，提出了动特性参数的测定原理和方法并进行实验研究，测得结果精度较高。

以上针对圆锥动静压轴承的研究多限于单一工况，针对圆锥动静压轴承在实际应用中多工况并存的问题，有必要建立多目标优化模型。本文作者在圆锥动静压轴承油膜静、动特性计算基础上，根据实际要求按照重要程度对各优化目标设定不同的加权系数，建立了同时考虑单位承载力下功耗、平均温升和失稳转速的多目标优化模型，采用有限元和复合形法联立求解并对优化结果进行分析。

1 圆锥动静压轴承数学模型

1.1 控制方程和边界条件

图1所示为圆锥动静压轴承结构示意图，轴瓦内壁均匀开设4个油腔，每个油腔包含深腔和浅腔，深腔起静压作用，通过小孔节流供油；浅腔和封油边起动压作用。

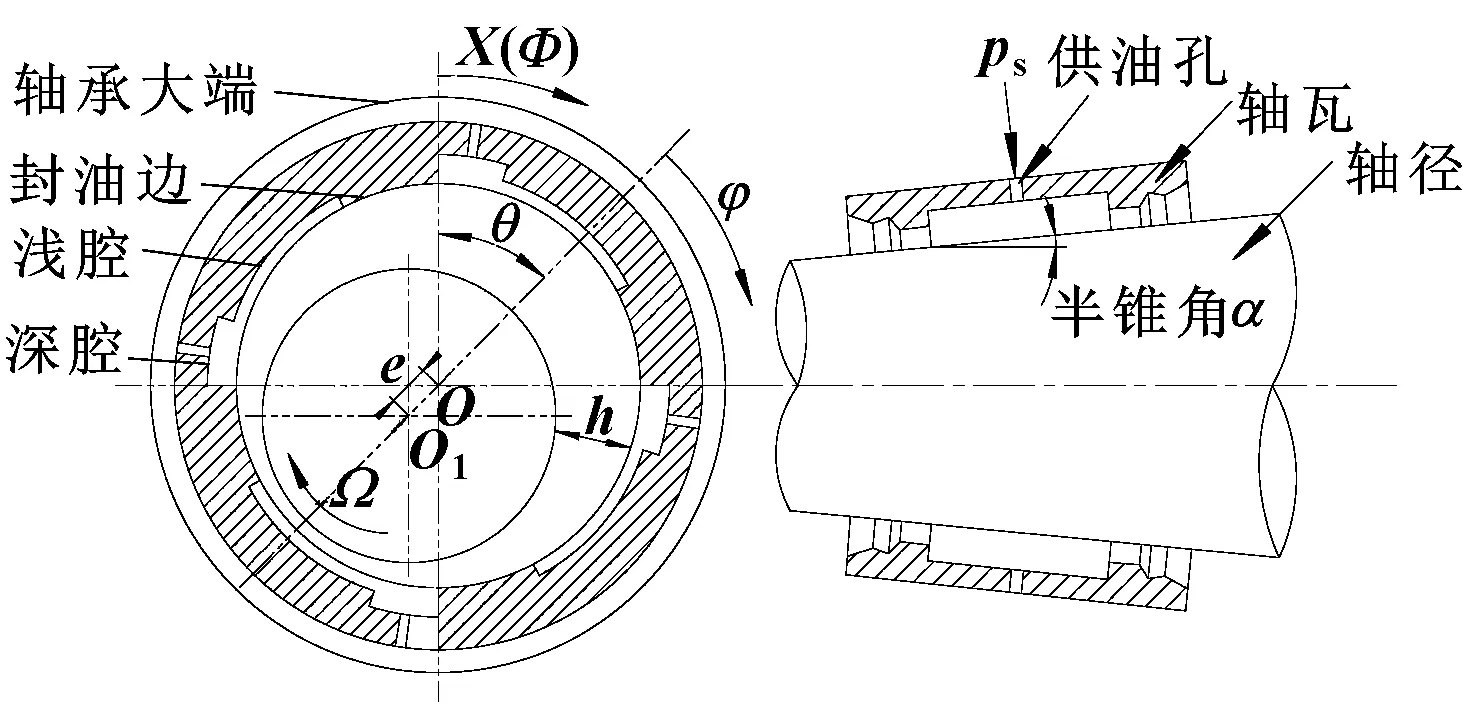
图1 圆锥动静压轴承结构示意Fig 1 Structure of conical hybrid bearing

假设润滑油为不可压缩流体，流动为层流，不计轴径轴瓦的弹性变形和轴线倾斜，取量纲一化参数如下：

则量纲一化动态Reynolds方程为

(1)

式中：BM=μ0Ωd2/(psc2)；a为半锥角；r为圆锥轴承展开后的扇形极径；l为轴承母线长度；c为半径间隙；d为轴承大端直径；h为油膜厚度；p为油膜压力；ps为供油压力；ε为偏心率；e为偏心距；ε0为静平衡时偏心率；Ω为轴径角速度；Φ为圆锥截面上的角坐标。

量纲一化油膜厚度为

(2)

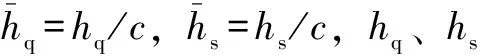
图2所示为圆锥轴承边界条件。油膜压力边界条件为

图2 圆锥轴承边界条件Fig 2 Conical bearing boundary conditions

(3)

深腔流量平衡方程为

(4)

式中：pr,m为第m个深腔压力；Γ1为轴承端面边界；Γ2为第m个深腔边界；Γ3为油膜破裂边边界；Rj,m为第m个深腔节流器液阻;qout、qin、qcout、qcin分别为第m个深腔4个方向的流入、流出流量参数。

1.2 静态特性参数

圆锥动静压轴承有x，y，z3个方向的油膜力：

(5)

径向承载力：

(6)

摩擦功耗为

(7)

端泄流量：

(8)

泵功耗：

(9)

平均温升：

(10)

式中：μ为润滑油的动力黏度；Cv为润滑油比热容；ρ为润滑油密度。

1.3 动态特性和稳定性参数

圆锥动静压轴承油膜有kij,bij(i，j=x，y，z)共18个刚度系数和阻尼系数，采用小扰动法求解动态Reynolds方程得到。将圆锥轴承-转子系统简化为图3所示的单质量刚性对称转子系统，量纲一化动力学方程为

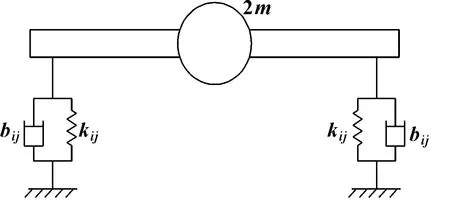
图3 圆锥动静压轴承-转子系统Fig 3 Conical hybrid bearing-rotor system

(11)

其中系数A～K是刚度和阻尼系数的线性组合。使用失稳速度来评价系统稳定性，那么系统运动方程的特征方程可以写成：

α0v6+α1v5+α2v4+α3v3+α4v2+α5v+α6=0

(12)

其中αi(i=0～6)为特征方程的系数，可用转子质量、油膜刚度、阻尼系数表示。根据Routh-Hurwitz准则，系统达到平衡状态的充要条件是：

(13)

通过迭代计算，直到满足式(13)时求解出失稳转速。具体求解方法可参考文献[7]。

2 圆锥动静压轴承多目标优化

圆锥动静压轴承多用于高转速、高精密旋转机械装备中，对油膜性能要求很高，在保证油膜具有一定的承载力和稳定性的同时，还需限制摩擦功耗和温升[8-10]。在不同工况条件下，各指标权重亦不同。例如，用于精密机床的轴承，应防止温升过高引起润滑油变稀及轴瓦热变形；而对于透平膨胀机组转子系统上的轴承，由于工作转速较高，要防止油膜震荡引发的严重后果[11-13]。综合考虑上述问题，以单位承载力下功耗最小、温升最低及失稳转速最高做为目标函数，将目标函数进行量级统一后，优化目标函数描述为

(14)

将目标函数进行线性规划，转换为单目标优化问题：

(15)

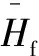
影响圆锥动静压轴承油膜特性的参数较多，通过计算发现，在不改变整体结构尺寸和油腔数量的前提下，浅腔包角θq(°)、封油边宽度Z1、Z2(mm)、半锥角α(°)的变化对优化目标影响显著，设计中取为优化参数。

优化设计变量的取值范围：

3 计算结果及分析

3.1 结构参数及优化变量

表1所示为圆锥动静压轴承初始结构参数。

供油压力为2 MPa，主轴转速n分别取15 000、20 000 r/min对圆锥轴承进行复合形法优化[14]。其中，方案一较为均衡，ζ1、ζ2、ζ3均取值为1；方案二对目标函数2控制严格，ζ1、ζ2、ζ3取值分别为ζ1=1，ζ2=2，ζ3=1。有限元及复合形法优化联立求解思路如图4所示。

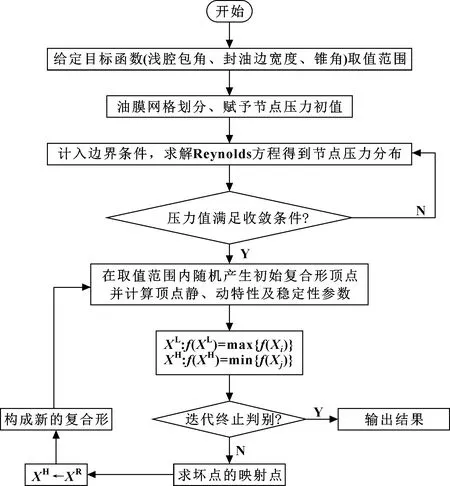
图4 圆锥动静压轴承优化计算流程Fig 4 Optimization calculation flow of conical hybrid bearing

3.2 优化结果分析

表2给出了主轴转速n=15 000 r/min，偏心率为0.4时2种优化方案和初始设计方案下各个单目标函数及多目标函数的计算结果。

由表2可知：相对于初始设计方案，2种优化方案的总优化目标和各单优化目标都有所改善，目标函数1和目标函数2得到降低，目标函数3则有所提升；同时可见，优化方案1对于目标函数1的优化幅度更大；其中目标函数1降低了43.9%，目标函数2降低了14.6%，目标函数3提升了24.3%。调整权重系数后，优化方案2对于目标函数2的优化幅度增大；其中目标函数1降低了28.4%，目标函数2降低了25.3%，目标函数3提升了10.6%。

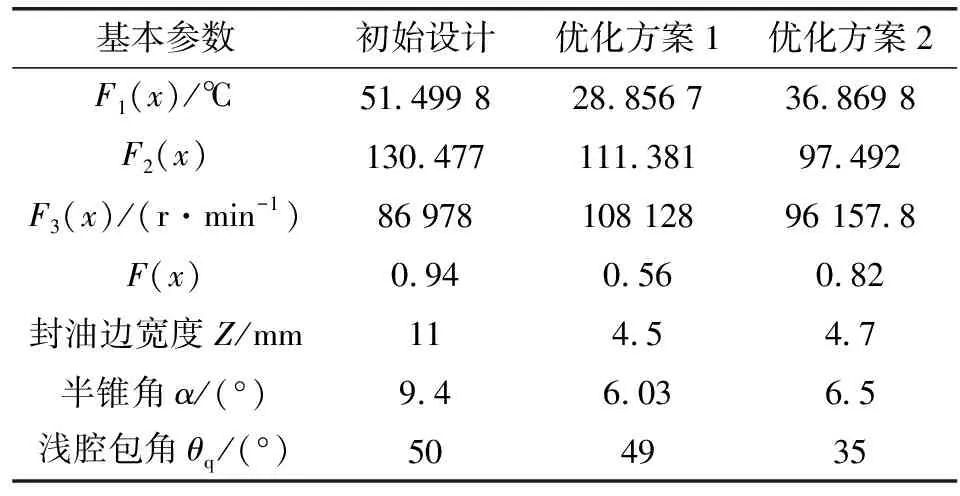
表2 优化参数及优化结果对比

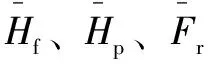
在确定优化参数的基础上，针对不同工况下各单目标函数进行了计算和比较。

图5所示为主轴转速分别取15 000、20 000 r/min时，2种优化方案下平均温升单目标函数随偏心率的变化规律。可以看出，相较于原始方案，优化方案1中2种转速下温升分别平均下降了43.6%和46.6%，而优化方案2则分别平均下降了31.02%和34.4%，说明在控制温升方面2种优化方案得到了很好的优化效果。

图5 目标函数1(温升最低)对比Fig 5 Comparison of objective 1(minimum temperature rise)

图6 目标函数2(单位承载力下总功耗最小)对比Fig 6 Comparison of objective 2(minimum totalpower consumption per unit capacity)

圆锥动静压轴承-转子系统的稳定性分析需要先计算9个刚度系数、9个阻尼系数，然后计算失稳转速。表3列举了主轴转速n=15 000 r/min，偏心率为0.1～0.4时，主要参数的变化情况。

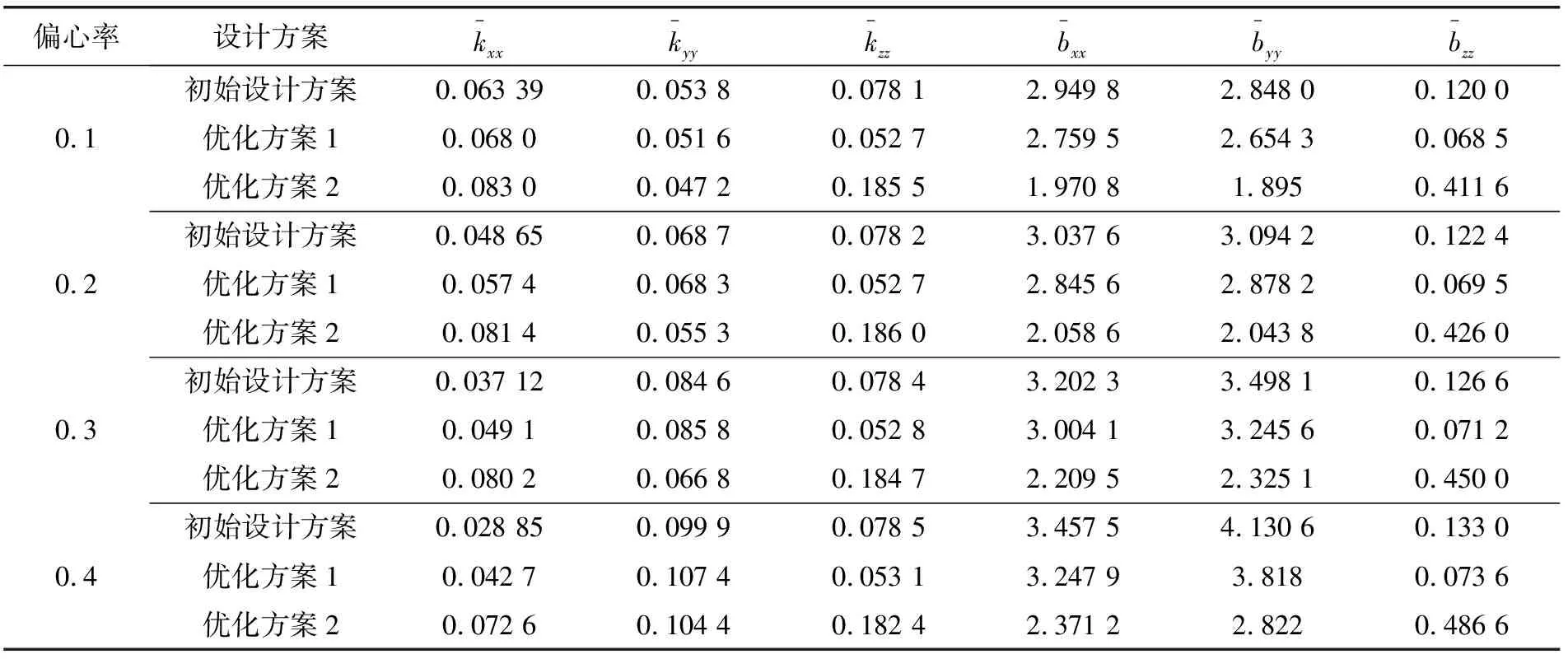
表3 稳定性系数对比

优化方案2中轴承浅腔包角较小，小偏心下油膜刚度较低，故稳定性劣于初始设计方案；偏心率的增大有利于增强油膜动压效应，油膜刚度随之增加，失稳转速大幅上升，稳定性优于初始设计方案。由图7可得，优化方案1和优化方案2在偏心率为0.4时，Nst分别增加了24.3%和17.3%，由此可见，相较于初始设计方案，2种优化方案下系统稳定性有所提高。

图7 目标函数3对比Fig 7 Comparison of objective 3

4 结论

(1)结合圆锥动静压轴承数学模型，利用复合形法对轴承结构参数进行多目标优化，当半锥角和封油边宽度明显减小、浅腔包角减小时，轴承平均温升、单位承载力下功耗得到了有效降低，失稳转速得到提高。

(2)单位承载力下功耗、温升及失稳转速均衡控制的优化方案1更适用于低温升、高转速的工况，而对单位承载力下功耗严格控制的优化设计2则更适合低功耗的设计。可见，通过对各优化目标设定不同的加权系数，可实现更低温升、更高转速和更低功耗等设计目标。