O形密封圈偏心情况下接触应力仿真研究*

杨 博 黄 乐 丁剑平 陈小影 谭 锋

(1.华南理工大学材料科学与工程学院 广东广州 510641；2.广州机械科学研究院有限公司 广东广州 510535)

O形密封圈是一种结构简单、 制造成本低且应用范围特别广的密封结构，在机械[1]、汽车[2]、航空[3]以及武器[4]的密封领域中起着重要的作用[5]。众多学者已经对O形密封圈的密封性能进行了较为深入的研究，其中也有大量研究应用了有限元软件。吴琼等人[6]利用ABAQUS分析了丁腈橡胶O形圈的静密封和微动密封性能。王军等人[7]利用ANSYS分析了基于渗透边界的O形组合圈密封特性。刘菁等人[8]利用有限元仿真软件对基于格来圈结构的O形密封圈进行动密封分析。康家明等[9]利用有限元分析软件ANSYS研究了沟槽形状对O形橡胶密封圈密封性能的影响。

由于O形圈模型是轴对称结构，在O形密封圈使用正常的情况下，整个密封圈受力均匀，各个位置压缩量相同，因此，研究者在利用有限元软件对O形密封圈进行接触应力的计算时，通常将复杂的三维模型简化为二维平面轴对称模型。该简化在不影响计算结果的前提下，可节省计算时间，大幅提高了计算效率[10-11]。然而，根据O形圈在工程中使用的实际情况来看，O形圈往往并不是完全轴对称，其在安装完成后会产生或多或少的偏移，这就造成O形圈受力不均匀，导致各个位置的压缩量也不同，即偏心现象。偏心现象直接导致三维模型不能简化为二维模型，因此对于偏心情况下接触应力的计算需要采取新的方法。

目前，对于O形圈偏心情况下的分析大多仍是采取简化的二维模型，其通过取偏心后O形圈的最大和最小压缩量作为二维模型的压缩量，达到利用二维模型计算偏心O形圈的目的。但实际上偏心O形圈发生偏心后其每个位置所受的预压缩量都有所不同，一般情况下，O形圈的一端承受最大的压缩量，对应的另一端承受最小的压缩量，而中间部分是从最大压缩量到最小压缩量的过渡。所以采用三维模型对偏心O形圈进行计算较为合理。

本文作者采用二维和三维模型，利用ABAQUS软件对O形圈偏心情况下的接触应力进行计算，探究二维模型计算结果的准确度以及偏心量和O形圈直径对于计算结果的影响。

1 有限元模型

1.1 橡胶材料的本构模型

文中主要利用ABAQUS软件对O形橡胶密封圈进行研究。在研究中，橡胶材料通常被认为具有不可压缩性，同时其具有高度非线性的特征，属于超弹性体。在ABAQUS中有多种材料模型可以表征超弹性体，包括基于热力学统计的Arrude-Boyce模型、Van der waals模型以及基于唯象学方法的Mooney-Rivlin模型、Yeoh模型和Ogden模型等。文中采用应用最为广泛的Mooney-Rivlin[12-14]模型，其应变能函数为

W(I1,I2)=C10(I1-3)+C01(I2-3)

(1)

式中：I1与I2为应力张量不变量；C10与C01为材料参数。文中研究O形密封圈所采用的橡胶材料，根据实验拟合，获得的C10为1.406 3 MPa，C01为0.171 3 MPa。

1.2 基本假设

有限元软件ABAQUS建立分析模型时，对模型做出以下几点假设[15]：

(1)O形密封圈橡胶材料具有各向同性且是完全弹性的；

(2)不考虑橡胶材料的应力松弛和蠕变特性；

(3)不考虑温度和时间对于橡胶材料的影响；

(4) 沟槽和杆的材料刚度远大于O形密封圈，可以忽略其变形的影响。

1.3 有限元模型

目前在O形密封圈偏心情况下,往往还是采用二维模型进行计算。以二维的方式计算O形密封圈接触应力的模型如图1所示。

图1 O形密封圈的二维模型Fig 1 Two-dimensional model of O-ring

二维模型一般选取偏心导致的最大和最小的压缩量进行计算。但由于偏心情况下O形圈各个位置压缩量的不同，同时二维模型进行计算只能选取特定的压缩量，因此二维模型虽然有着计算快的优点，但模型的简化在偏心情况下不具有合理性，导致计算数据的可信度也不高。

计算O形圈偏心情况下的三维模型如图2所示。由于偏心O形圈具有对称性，为方便计算只需构建三维模型的1/2，并在截面上设置对称边界条件即可。 O形圈的预压缩通过平板的向下位移实现，其中每一处的预压缩都不同，图2中从最左侧到最右侧O形圈的预压缩在不断增大。O形圈最左侧的压缩量为二维模型所采取的最小压缩量，O形圈最右侧的压缩量为二维模型所采取的最大压缩量。

图2 O形密封圈的三维模型Fig 2 Three-dimensional model of O-ring

2 分析结果

2.1 无偏心情况下密封圈的接触压力

为方便利用二维模型和三维模型对O形密封圈的偏心情况进行研究，首先利用二维模型和三维模型对O形圈无偏心情况的接触压力进行计算，并比较2种模型在无偏心情况下的计算结果。计算时以截面直径为3.55 mm，O形圈直径为50 mm，预压缩量为0.65 mm，偏心量为0.05 mm的O形圈为例。

图3所示为无偏心情况下O形密封圈二维模型计算得到的接触应力分布。计算时利用ABAQUS的自适应网格功能对密封圈的网格进行细划分，可以明显看到随着网格的细划分，接触应力最大值变化并不是很明显，因此最初划分的网格所得到的结果是可靠的。为保证误差的最小值，下文研究中对于无偏心以及偏心的二维模型所采取的网格将与这次采取的网格保持一致。

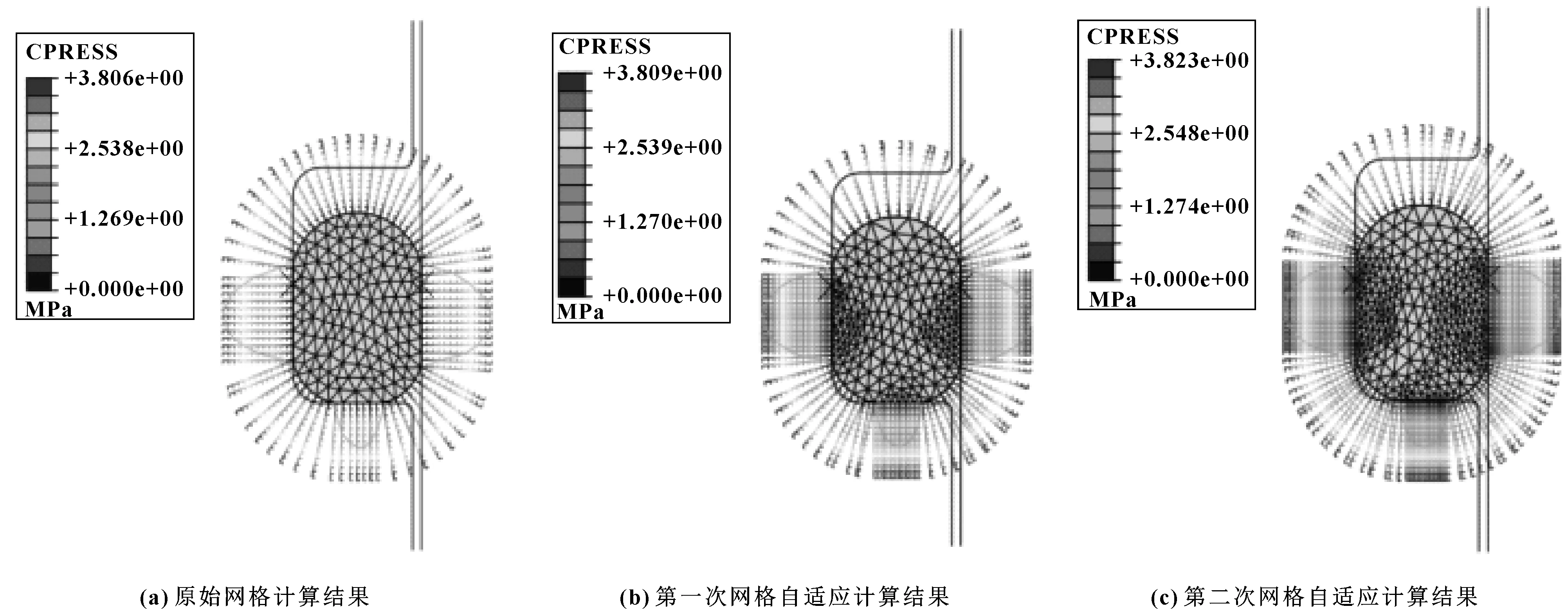
图3 无偏心情况下O形密封圈二维模型接触应力的网格自适应计算结果Fig 3 Mesh adaptive calculation results of contact stress of two-dimensional model of O-ring without eccentricity(a)calculation results of the original grid;(b)calculation results of the first grid adaptivecomputation;(c)calculation results of the second grid adaptive computation

图4所示为无偏心情况下三维模型计算得到的O形圈接触应力分布。其中O形圈截面网格密度与二维模型中网格密度一致。

图4 无偏心情况下O形密封圈三维模型的接触应力计算结果Fig 4 Calculated contact stress of three-dimensionalmodel of O-ring without eccentricity

将图3中压缩杆与O形圈之间接触应力数据，与图4中最右侧压缩板与O形圈之间接触应力数据进行比较，如图5所示。可以观察到图中两条接触应力曲线几乎重合在一起，而且最大接触应力值相差很小，这说明O形圈无偏心情况下采用二维模型和三维模型的计算结果近似相等。因此在O形圈偏心情况下二维模型与三维模型计算结果可以直接进行比较。

图5 无偏心情况下O形密封圈二维模型和三维模型的接触应力对比Fig 5 Comparison of contact stress between two-dimensionalmodel and three-dimensional model of O-ringswithout eccentricity

2.2 偏心量的影响

分别取偏心量为0.05、0.10、0.15、0.20、0.25 mm，对O形密封圈二维和三维模型的接触应力进行计算与比较，探究不同偏心量下二维模型计算结果的准确性。文中采取控制变量法对不同因素进行探究，其中截面直径取3.55 mm，正常预压缩量取0.65 mm，O形圈直径取50 mm。

图6所示为偏心量为0.05 mm时二维模型计算的最大和最小压缩量下的接触应力分布，图7所示为偏心量为0.05 mm时三维模型计算的接触应力分布。

图6 偏心量0.05 mm下O形圈二维模型的接触应力计算结果Fig 6 Calculated contact stress of two-dimensional model of O-ring under eccentricity of 0.05 mm (a) contactstress at maximum compression;(b)contact stress at minimum compression

由于ABAQUS软件后处理的局限性，对于二维模型的接触应力分布结果展示不是很直观，而且三维模型的接触应力值也无法从云图中直接得到。为方便观察比较，文中从模型中提取出最大和最小压缩量所对应的O形圈与压缩杆的接触应力分布情况并进行比较。图8所示为二维模型最大和最小压缩量时各个偏心量下的接触应力计算结果，图9所示为三维模型最大和最小压缩量时各个偏心量下的接触应力计算结果。

图8 不同偏心量时二维模型在最大和最小压缩量下的接触应力分布Fig 8 Contact stress distribution of two-dimensional model under maximum and minimum compression with different eccentricity (a)contact stress distribution at maximum compression;(b)contact stress distribution at minimum compression

根据上述接触应力分布情况，可以得到不同偏心量下的最大接触应力值以及二维型的计算误差，如表1所示。其中相对偏心量为偏心量与正常预压缩量的比值，二维计算的误差为二维结果和三维结果的差值与三维结果的比值。从表1可以看出，对于任意偏心量，在最大压缩量处二维模型计算结果大于三维模型，在最小压缩量处二维模型计算结果小于三维模型；同时二维模型计算误差绝对值都随着偏心量的增大而增大。对误差变化进行拟合，得到：

表1 不同偏心量下最大接触应力值以及二维模型计算误差

y1=0.036 4x

(2)

y2=-0.144x

(3)

式中：y1为最大压缩处二维计算误差；y2为最小压缩处二维计算误差；x为相对偏心量。

可见，最大压缩量处误差增加率小于最小压缩量处。

对于截面直径为3.55 mm，密封圈直径为50 mm的O形密封圈，在任意偏心量下，通过公式(2)(3)计算出的误差可以修正二维模型的计算结果，得到更加准确的接触应力预测值。

2.3 O形密封圈直径的影响

O形密封圈直径分别取14、30、50、60 mm，对二维和三维模型接触应力进行计算与比较，探究不同O形圈直径下二维模型计算结果的准确性。文中采取控制变量法对不同因素进行探究，其中截面直径取3.55 mm，正常预压缩量取0.65 mm，偏心量取0.15 mm。

从模型中提取出最大和最小压缩量所对应的O形圈与压缩杆的接触应力分布情况进行比较，如图10、11所示。图10所示为二维模型最大和最小压缩量时各个O形圈直径下的接触应力计算结果，图11所示为三维模型最大和最小压缩量时各个O形圈直径下的接触应力计算结果。

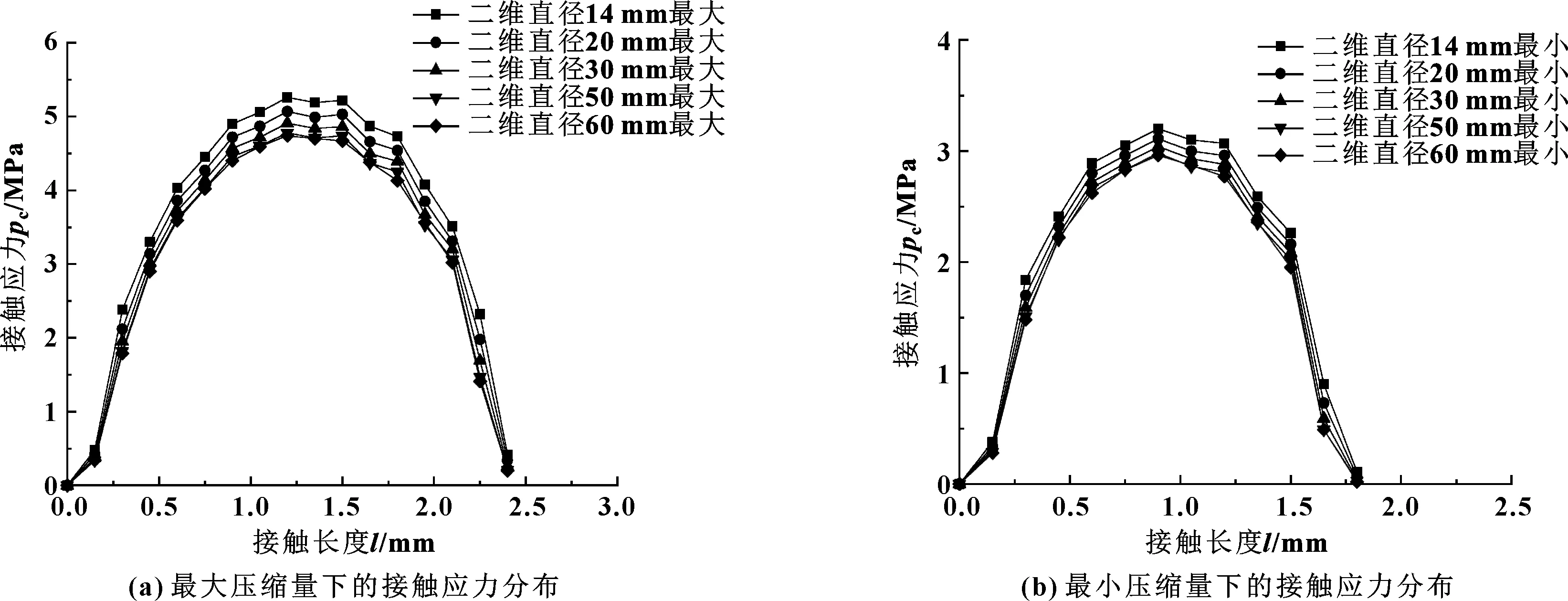
图10 不同直径的O形圈二维模型的最大和最小压缩量下的接触应力分布Fig 10 Contact stress distribution of two-dimensional model under maximum and minimum compression with different O-ring diameters(a)contact stress distribution at maximum compression;(b)contact stress distribution at minimum compression

根据上述接触应力分布情况，可以得到不同密封圈直径下的最大接触应力值以及二维计算误差，如表2所示。可以看出，对于任意的O形圈直径，在最大压缩量处二维模型计算结果大于三维模型，在最小压缩量处二维模型计算结果小于三维模型；同时随着O形密封圈直径的增加，无论是最大压缩量处还是最小压缩量处，二维模型计算误差的绝对值均呈现出变小的趋势。对误差变化进行拟合，得到：

y1=1 885.63x-1.964

(4)

y2=-78.04x-0.826

(5)

式中：y1为最大压缩处二维计算误差；y2为最小压缩处二维计算误差；x为O形圈直径。

对于截面直径为3.55 mm，偏心量为0.15 mm的O形密封圈，通过公式(4)(5)计算出的误差可以修正二维模型的计算结果，得到更加准确的接触应力预测值。

3 结论

(1)以二维模型计算偏心情况下O形密封圈的接触应力时，最大压缩量处的计算结果大于三维模型计算结果，最小压缩量处的计算结果小于三维模型计算结果。

(2)随着偏心量的增大，二维模型计算结果误差不断增加，随着O形密封圈直径的增大，二维模型计算结果误差不断减少。

(3)通过拟合得到二维模型的误差预测公式，可以对不同偏心量和不同O形圈直径的二维模型计算误差进行预测。