表面亲疏水特性对毛细管内双组分渗流特性的影响*
陈春辉 周剑锋 邵春雷
(南京工业大学机械与动力工程学院 江苏南京 211816)
螺栓法兰垫片静密封连接结构广泛应用于承压设备和管道,理论上密封面之间的间隙不可能完全消除,因此泄漏无法避免,但可以控制在能接受的范围。一般来说,静密封连接结构的泄漏形式分为2种,即界面泄漏和渗透泄漏。界面泄漏是指介质通过法兰与垫片的交界面逸出的泄漏,这种泄漏的程度主要取决于界面的间隙大小。为了研究界面泄漏,人们提出了3种泄漏模型,即平行圆板模型、三角沟槽模型和多孔介质模型[1-3]。渗透泄漏是指介质通过垫片毛细管的泄漏,这种泄漏主要与材料的物理特性有关。可以认为,大多数非金属垫片和金属-非金属复合垫片材料近似为多孔介质[4]。对于气体,假定多孔介质各向同性,气体流过多孔介质的流道由n个弯弯曲曲、半径大小不等的毛细管组成,按Hagen-Poiseuille公式(以下简称H-P公式)计算,则气体通过多孔介质的层流流率LL为
(1)
式中:p1为管道入口处压力;p2为管道出口处压力;ri为通道半径;η为流体的动力黏度;li为通道的长度。
压缩状态下,毛细管的形状发生改变,式(1)要根据试验结果进行校正。
对于非圆截面管道,可采用水力当量直径Dh代替式(1)中的ri进行计算。根据流体力学对于非圆截面水力当量直径的表述,即非圆截面管道的水力当量直径是圆截面水力当量半径的4倍,故水力当量直径的表达式应如式(2)所示。对于湍流,由于流速分布比较均匀,计算误差在2%左右;而对于层流,由于非圆形截面的壁面周边的速度与圆截面的情况差别较大,误差较大(可能超过20%)。
(2)
式中:A为管道截面积;P为浸润周边长。
目前常用的静密封泄漏预测方法多基于H-P公式。而对于复杂组分的泄漏模型,由于组分在毛细管内的流动情况十分复杂,尚未有可行的方法。对于毛细管内的双组分渗漏,一方面要考虑组分之间的相互影响,另一方面要考虑毛细管壁面特性对流动的影响,较之于单组分渗漏,情况更加复杂。本文作者采用格子玻尔兹曼方法(LBM)模拟毛细管内双组分的流动过程,可以同时考虑双组分作用和壁面特性对渗漏的影响,进而获得壁面亲疏水特性对渗流的影响规律[5]。
1 物理模型
泄漏通道表面形貌异常复杂,研究人员利用分形理论等对粗糙的泄漏通道进行了简化。为便于分析,文中将截面随机变化的泄漏通道简化为具有当量截面积和水力周长的矩形截面微通道,如图1所示。
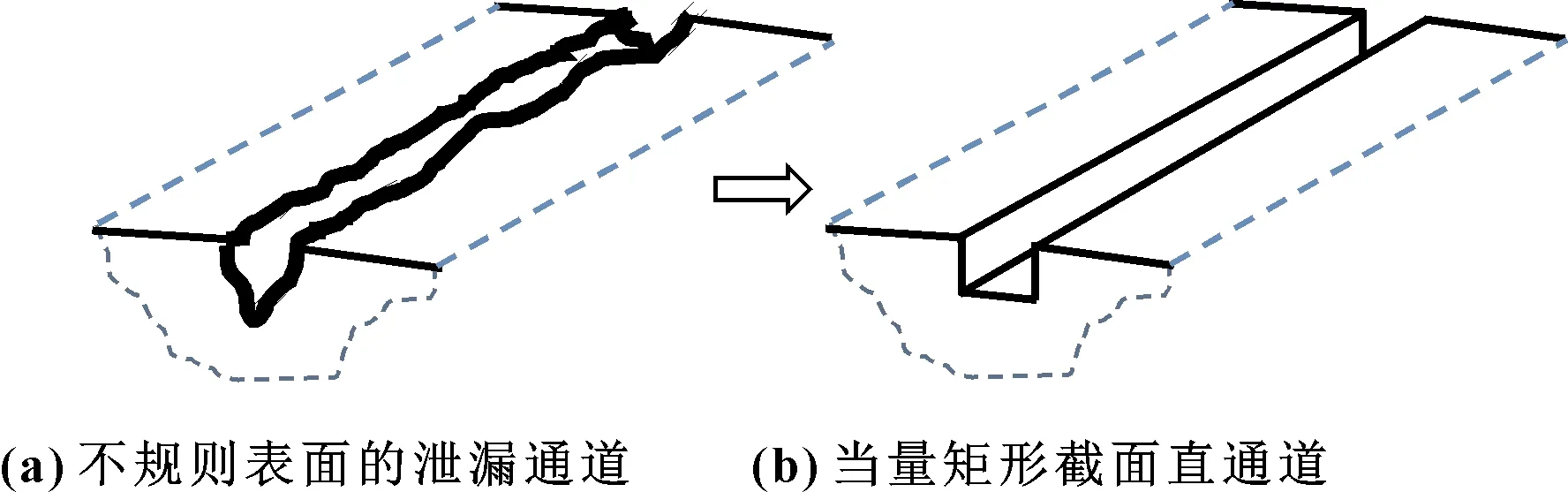
图1 不规则泄漏微通道简化为当量矩形截面直通道Fig 1 Simplification of irregular leak path(a) into equivalentrectangular section straight channel(b)
根据垫片的工况条件及简化的微通道,可以建立如图2所示的矩形微通道流动模型。介质由高压侧经矩形微通道流向低压侧,介质的主相为轻密度相,分散相为重密度相(液滴)。通道两端为流体的进出口边界,流动由通道两端的压差产生[6-8]。
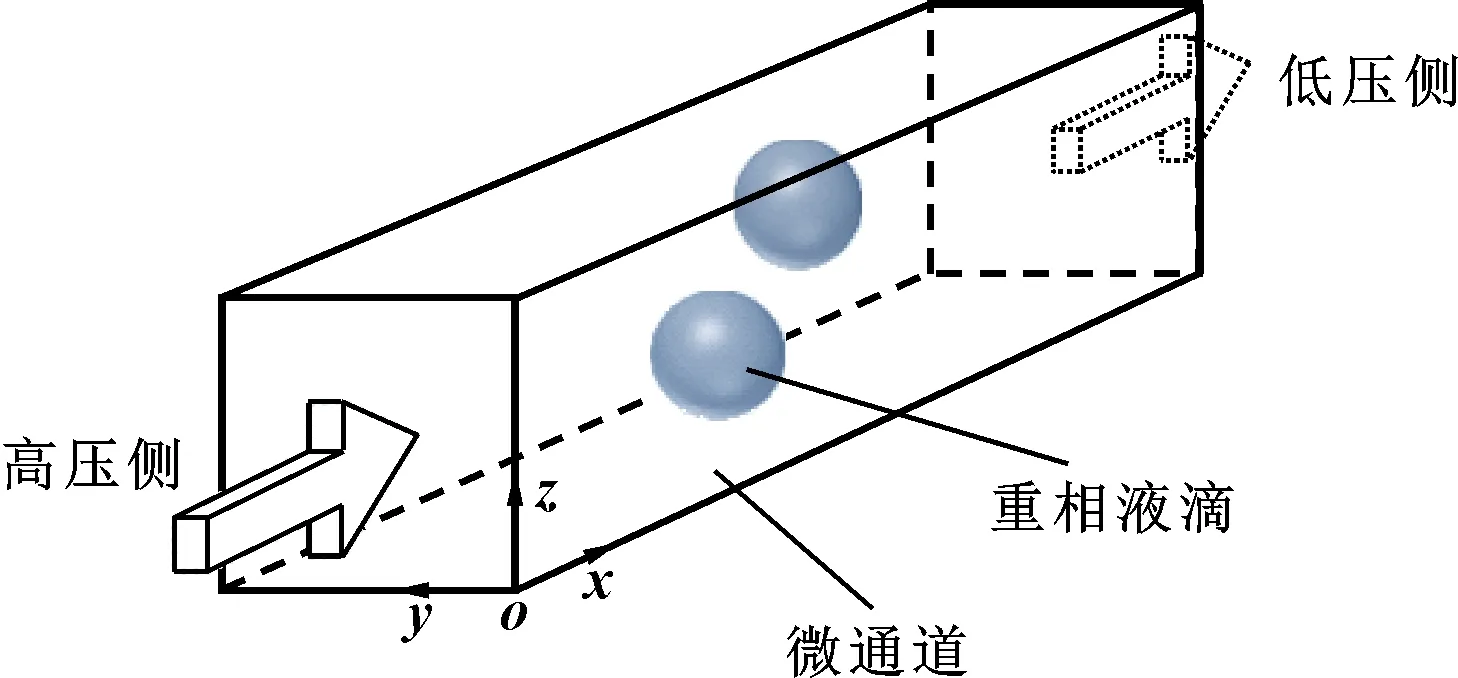
图2 矩形微通道内双组分流动模型Fig 2 Bicomponent flow model in rectangular microchannel
2 微流道内双组分流动的格子玻尔兹曼模拟方法
对于两相流动的LBM模拟,国内外学者提出了多种模型。SWIFT等[9]以多相多组分流体的自由能理论和热力学为基础,提出了自由能模型(一种多相LBM模型)。TAKADA等[10]和FRANK等[11]利用自由能模型成功模拟气泡上升过程;HAO等[12-13]利用自由能模型模拟液滴的变形过程和多孔介质内的气液两相流现象。HE等[14]模拟了三维Rayleigh-Taylor不稳定问题,形象地描述了2种液体的交融过程。
文中采用HE等[14]提出的两相流(双组分)模型进行模拟,2种组分的分布方程分别如式(3)和(4)所示,其中gi和fi能分别回归到不可压缩流动的纳维斯托克斯方程(N-S方程)和界面追踪方程[15]。
(3)
(4)

(5)
(6)
其中,ωi是权重系数;p和ρ分别是流体的压力和密度;eiα和eiβ是离散速度;uα和uβ是x和y方向的速度分量;宏观变量的计算方法参见文献[14],即
φ=∑fi
(7)
(8)
(9)
其中,ρ是宏观密度;u是宏观速度矢量;ψ是ρ或φ的函数,ψ(ρ)和ψ(φ)与流体动力学的压力p和热动力学的压力pth有关[16]。
(10)
(11)
其中pth根据Carnahan-Starling状态方程[14,16]计算,即
(12)
若指数函数φ(x,t)已知,则可根据式(13)、(14)、(15)分别确定流体的密度(ρ)和运动黏度(ν)以及弛豫因子τ1。
(13)
(14)
(15)

3 结果与讨论
3.1 矩形通道内的速度分布规律



图3 单一组分在微通道内的速度分布规律Fig 3 Velocity distribution of a single component inmicrochannel(a) the flow distribution of light 1.5×10-4);(b) the flow distribution of

图4 纯轻相介质在微通道内的速度变化Fig 4 Velocity variation of pure light phasemedium in microchannel
3.2 球形重相液滴在微通道内的运动特性

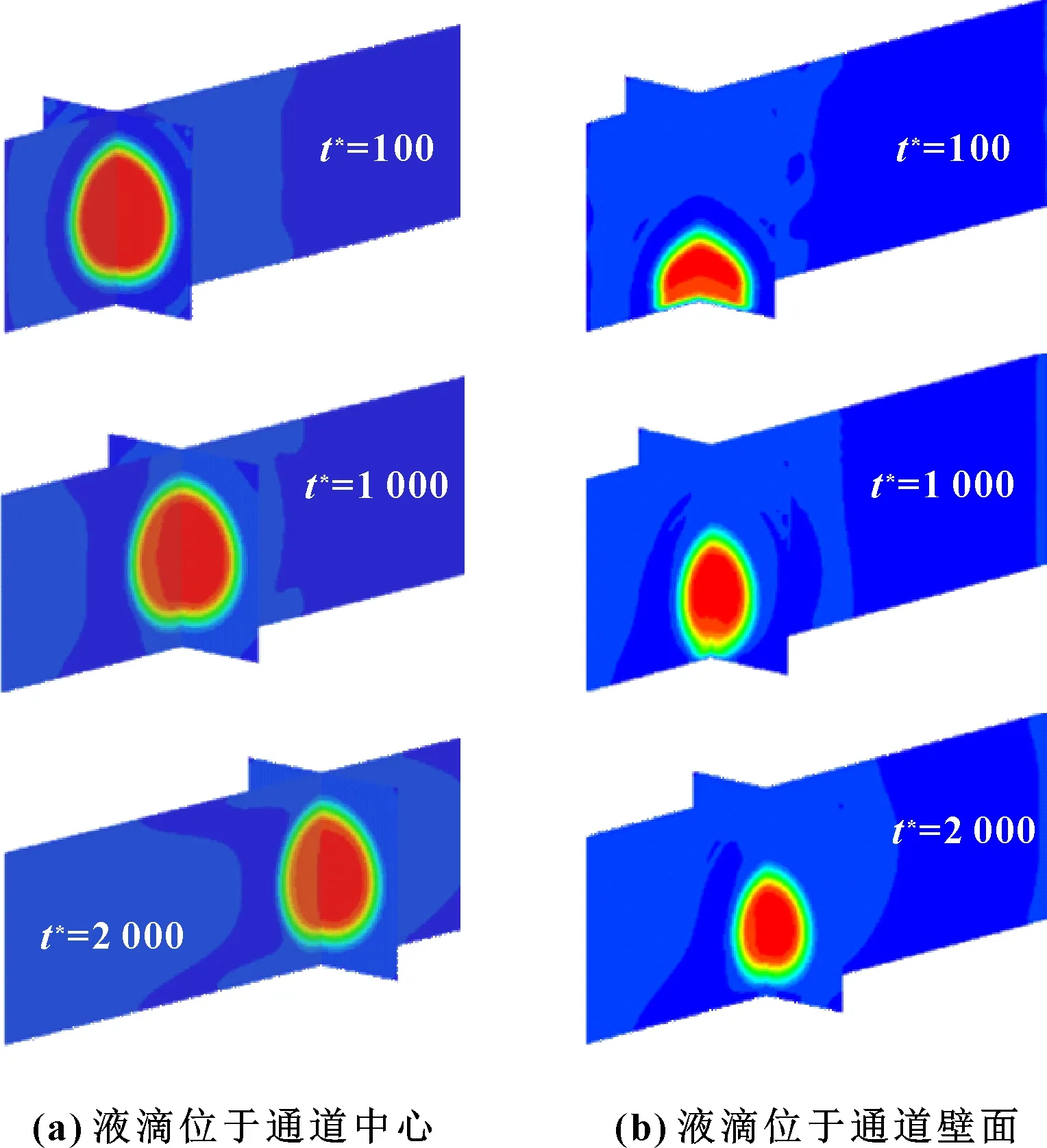
图5 重相液滴在轻相中的运动情况Fig 5 Motion of heavy phase droplet in light phase(a) thedroplet located in the center of microchannel;(b)the droplet located on the wall of microchannel
图5(a)中液滴速度的变化如图6所示。重相液滴的速度呈现波动上升趋势,这是由于流动过程中重相和轻相之间不断相互作用,液滴在前进的过程中不断调整形状,甚至约在3 000步和5 000步的时候速度出现了较大波动。

图6 位于通道中心的液滴的速度变化规律Fig 6 Velocity variation of the droplet located inthe center of microchannel


图7 不同壁面性质下位于通道中心的液滴的速度变化规律Fig 7 Velocity variations of droplet located in centerof microchannel under different wall properties
3.3 环形重相组分对轻组分流动的影响
对于亲水性壁面,重相分布最终将紧贴于矩形微通道壁面,因此,为了缩短模拟时间,在模拟的初始时刻,在局部壁面处设置如图8所示的环形重相。模拟开始后,重相开始在壁面扩展,并由于轻相的拖动,在壁面爬行。ΔLx为环形液膜的轴向宽度,h为液膜的厚度。

图8 初始时刻的环形重相模型Fig 8 Ringlike heavy phase model at initial time
对于初始时刻为环形的重相模型,在约2 000步的时候,重相的形状基本调整完毕,其构成了光滑边缘的孔状结构,如图9(b)所示。对于如图9(a)所示的初始时刻只有半球的模型而言,虽然同样由于表面张力的作用,重相在槽道底面铺开,但由于体积分数较小,对通道的流道截面的影响不如环形重相显著。

图9 亲水性壁面上重相的分布规律Fig 9 Distribution of heavy phases on hydrophilic wall(a)hemispherical heavy phase model at initial time;(b) ringlike heavy phase model at initial time
研究发现,对于亲水性壁面,重相的体积分数对流道截面的型式影响显著。将重相体积分数δ定义为
δ=VF/VP
(16)
式中:VF为重相的体积,VF=ΔLx(2Lyh+2Lzh-4h2);VP为通道的体积,VP=LxLyLz。
图10所示为2种不同体积分数重相条件下,轻相的速度变化规律。当δ较大时,对通道的堵塞作用更明显,通道的阻力更大,因此轻相的速度较小。
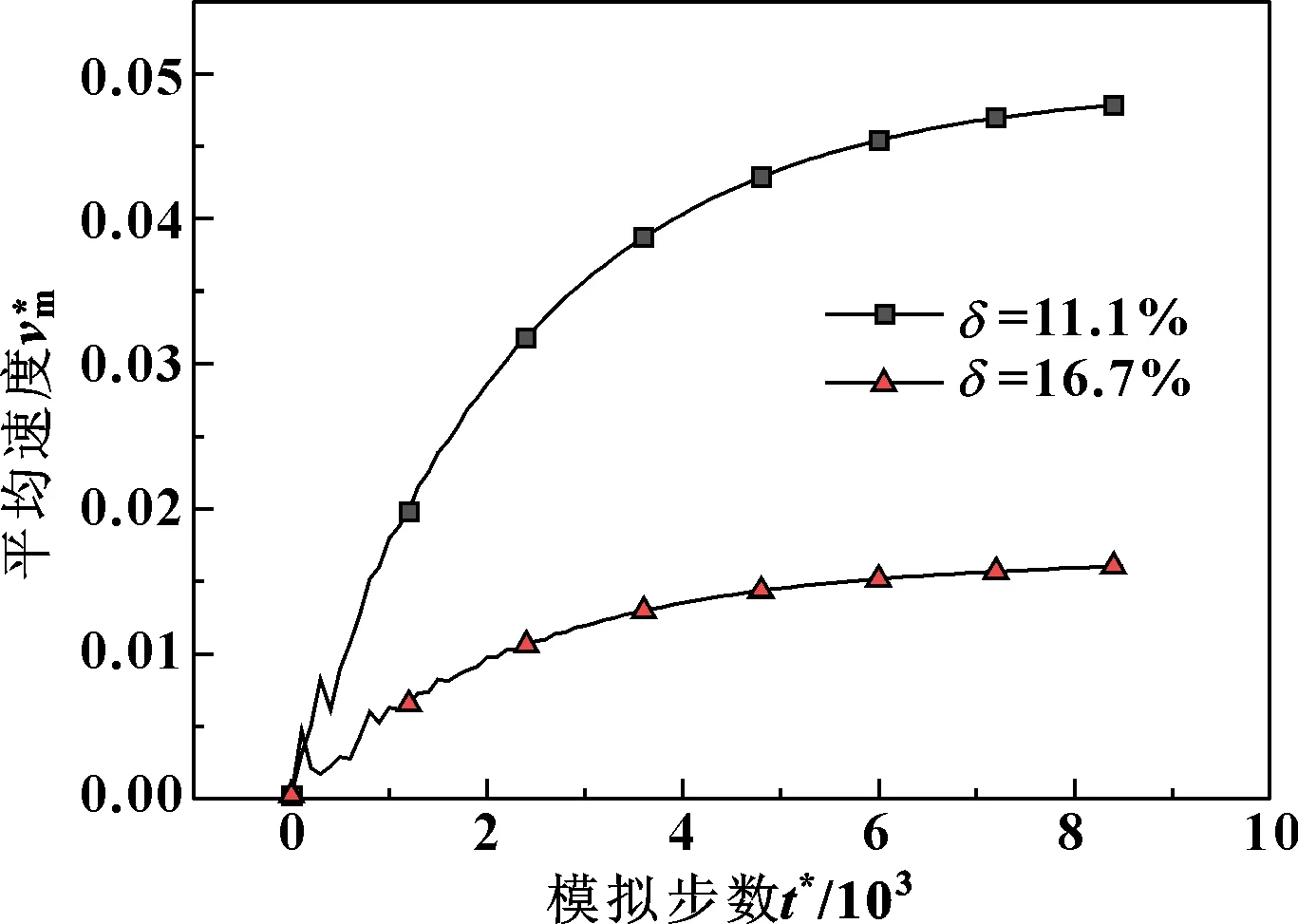
图10 重相体积分数对轻相速度的影响Fig 10 Influence of heavy phase volume fractionon light phase velocity
4 模拟结果与H-P公式计算结果的比较
根据式(1),可以计算单相介质在一定压差条件下的渗漏率。而根据LBM模拟结果,可以确定通道内轻相的平均流速,进而可以计算得到体积流量,即v*Y*Z*。表1列举了8组参数条件下LBM模拟结果与H-P公式计算结果。

表1 LBM模拟结果与H-P公式计算结果
由表1可知,8组数据中,除第2组数据和第7组数据外,LBM模拟渗漏率均大于H-P公式计算渗漏率。对于纯轻相和纯重相组分的流动(第1和2组数据),由于重相的黏度大,所以纯重相的渗漏率明显小于纯轻相的渗漏率。从表1中亦可以看出,随着重相体积分数的增加,渗漏率明显减小。在采用H-P公式计算时,使用的黏度是根据2种物质黏度和其所占体积分数折算得到的当量黏度,这与LBM模拟发现的两相流渗流状态的偏差较大,说明采用当量黏度计算渗漏率存在较大偏差。另外,H-P公式计算时采用了当量直径,这也给计算结果带来了一定误差。
5 结论
采用LBM研究了微通道内双组分的流动过程,考虑通道壁面效应对组分的影响,研究2种密度不同的组分在通道内的流动特性。得到以下结论:
(1)通道壁面的亲水、疏水特性对双组分的流动影响十分显著,特别是亲水壁面,重相在壁面上的黏滞,使通道的截面尺寸减小,最终使得轻相的体积流量变小。
(2)重组分在亲水性泄漏通道壁面上的黏滞,有利于减小渗漏。
(3)双组分在亲水性壁面通道内的流动不同于一般的双组分混合流动,因此在利用H-P公式建立泄漏预测模型时需要采用合适的校正方法。

