隧道Park收敛模式正交下穿既有隧道影响分析

靳军伟， 付柏毅， 陈允斌， 刘钢立， 李明宇

(1.郑州大学 土木工程学院，河南 郑州 450001； 2.山东正元建设工程有限责任公司，山东 济南 250014；3.中铁十五局集团城市轨道交通工程有限公司，河南 洛阳 471000)

0 引言

随着我国大中城市地铁隧道的大规模建设，新建隧道与既有地下结构，如桩基础[1]、管线[2]、管廊[3]等近接施工的情况也越来越频繁。特别地，新开挖隧道与既有隧道相互影响的问题已成为影响城市地铁安全运营的重要因素。

现有的针对新开挖隧道与既有隧道相互影响的研究，按照研究手段的不同，可以分为模型试验法、理论研究以及数值模拟法[4-6]。目前针对隧道正交下穿既有地铁隧道的分析研究多使用数值模拟的方法，从隧道边界控制条件来看，可分为力控制方法(FCM)和位移控制方法(DCM)。

隧道施工数值模拟的力控制法主要通过控制隧道掘进过程中隧道周围边界的压力值，如掌子面压力，注浆压力等参数来计算。Kavvadas等[7]通过施加面荷载考虑了掌子面压力和注浆压力等因素在土压平衡盾构三维施工模拟中的作用，但其对地表变形的预测效果不佳，认为需要引入更加复杂的本构模型才能实现；Peng等[8]使用力法对气压沉箱的具体施工过程进行了模拟，研究了气压沉箱法施工对周围地层的影响，但由于模拟中刀盘切割和挤压作用对周围土体产生反复的扰动而无法对周围土体位移进行精确描述。同时，力控制法用于模拟盾构隧道施工时，无论是在平面应变还是在三维条件下，常会导致更浅、更宽的地面沉降槽以及更高的远场沉降[9-11]。为了克服这个问题，Cheng等[12]提出基于隧道二维平面变形的位移控制方法(DCM)，随后被诸多学者广泛应用于隧道开挖的相关岩土工程问题。

与力控制方法相比，位移控制方法的优势在于能够准确把握隧道收敛变形[13]，同时，考虑到隧道边界的收敛模式对结果有着重要的影响，位移控制方法可以采用更能反映隧道实际变形的非均匀收敛模型而不是简单的均匀收敛模型，因此在研究隧道正交下穿既有地铁隧道影响中，位移控制方法可以作为一种有效的研究手段。

在收敛控制模型研究方面，目前针对隧道边界的位移控制方法研究大多采用Park[14]提出的隧道边界收敛模型，因其模型数学公式较为简单，且对隧道收敛形式的概括比较全面。Cheng等[12]基于Park收敛模式，采用数值模拟验证了圆形非均匀收敛模式应用于位移控制方法的可行性，但研究中并没有深入讨论Park其他几种收敛模式的差异。

Park[14]将隧道边界的变形概括为4种收敛模式并给出了不同模式下的隧道边界收敛位移计算公式，因此本文将4种不同的收敛模式应用于隧道正交下穿既有地铁隧道的问题中，通过与既有工程案例的对比分析，给出Park收敛边界在位移控制方法中的适用性及地表沉降和既有隧道的变形规律。

1 Park的隧道收敛模式

开挖隧道的Park收敛模式分为4种，如图1所示：均匀收敛(BC-1)、圆形非均匀收敛(BC-2)、椭圆形收敛(BC-3)以及考虑隧道底部隆起变形的椭圆形非均匀收敛(BC-4)。在极坐标系中，不同收敛模式下隧道边界的收敛位移可以通过式(1)～ (4)计算：

BC-1:ur(r=a)=-u0;

(1)

BC-2:ur(r=a)=-u0(1+sinθ);

(2)

(3)

(4)

式中：ur为隧道边界各点收敛位移；a为隧道半径；u0=g/2,g为间隙参数，代表隧道拱顶的径向位移。

图1 Park的隧道收敛模式[14]Figure 1 Tunnel convergence pattern of Park[14]

得到间隙参数g，即可根据公式推断出隧道边界各点的位移量。由于土体损失是盾构施工导致土体位移的主要原因[15]，可以采用土体损失率来对g值进行计算。土体损失率可以通过经验方法、反分析方法、现场实测法和理论方法[16]获得。根据Loganathan等[17]的研究，隧道以BC-1和BC-2方式收敛的情况下，间隙参数与土体损失可以通过式(5)建立关系：

(5)

则在已知土体损失率的情况下，间隙参数g可以通过式(6)获得：

(6)

除了使用土体损失率计算得到外，间隙参数g也可以利用Lee等[18]提出的计算公式获得，如式(7)所示：

(7)

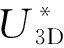
Loganathan等[17]的研究指出，在不排水情况下，采用土体损失和间隙参数的相互计算主要有两个优点：①可以考虑各种施工方法和隧道设备配置；②可以考虑土体的弹塑性性质，因此本文选择采用土体损失来对间隙参数进行计算。

为了能将隧道收敛位移转化为可输入的数据，以隧道变形前的轮廓为基准建立如图2所示的笛卡尔坐标系(以BC-2为例)，根据简单的几何关系，隧道边界各点在X、Z方向的收敛位移可以分别利用下式得出：

uX=ur·cosθ；

(8)

uZ=ur·sinθ。

(9)

根据不同的隧道边界收敛位移公式，根据式(8)、(9)可分别获得开挖隧道边界各点在X、Z方向的收敛位移，将该位移作为位移边界条件输入计算软件中对隧道周围土体位移进行计算，进而对上部既有隧道变形状况进行研究。

图2 基于隧道变形前圆心建立的坐标系Figure 2 Coordinate system based on the center of the tunnel before deformation

Cheng等[12]已在BC-2的条件下使用位移控制方法对单隧道开挖引起的隧道周围土体位移和地表沉降进行了模拟，研究表明,在BC-2条件下，位移控制方法在单隧道开挖土体位移预测方面具有良好的适用性，因此本文同样先采用Park非均匀收敛模型BC-2针对双隧道下穿的情况进行模拟以验证位移控制方法在双隧道应用中的合理性，然后对不同隧道收敛模式对地表沉降和既有隧道拱底变形的影响进行研究。

2 案例分析

2.1 计算模型

深圳地铁9号线梅村至上梅林隧道位于福田区，4号线既有隧道外直径6 m，周围的土层主要由填土,粉质黏土,砂质黏土和全风化、高度风化的混合岩组成，地层结构以及隧道相对位置如图3所示。

图3 地层结构以及隧道相对位置[19]Figure 3 Stratum and relative position of tunnels[19]

新建隧道埋深约17 m，上半部为砂质黏土，下半部为全风化混合岩。隧道外直径均为6.3 m，间距为9.9 m，隧道间距大于1.5D，因此认为相邻隧道的变形形式与土体损失关系较大，而与各自变形形状关系较小，适用于Park收敛模式分析。新建隧道与深圳4号线既有隧道净距为2.5 m，总土体损失率取1.5%。分层土体物理力学参数见表1，土体选用摩尔库伦本构模型。既有隧道衬砌参数见表2，采用线弹性模型，计算模型见图4。

表1 分层土体物理力学参数[19]Table 1 Physical and mechanical parameters of soil layers[19]

表2 既有隧道衬砌参数[19] Table 2 Lining properties of existing tunnel[19]

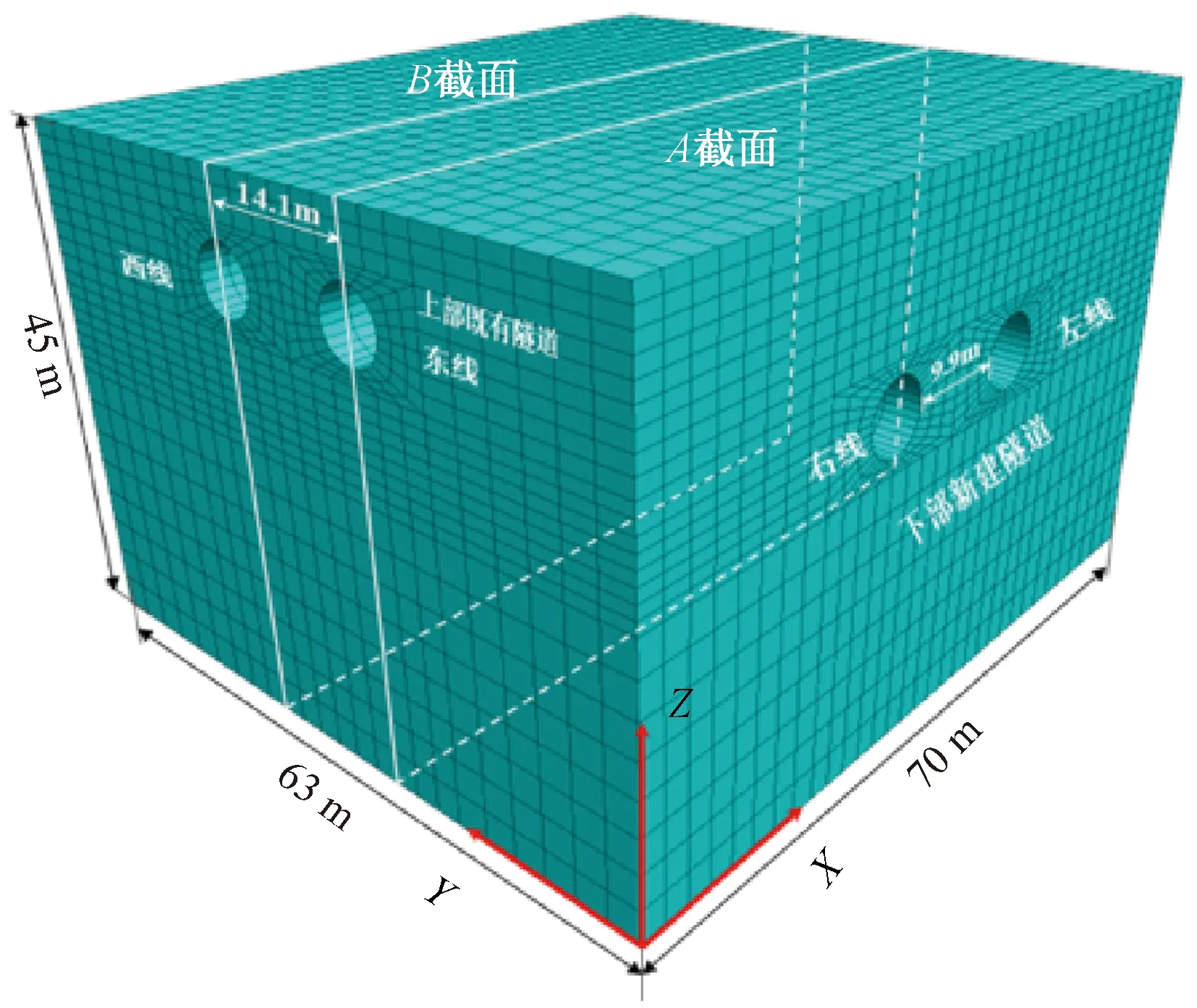
图4 位移控制方法计算模型Figure 4 Displacement controlled method computational model

模型在X、Y、Z方向上的尺寸分别为70 m、63 m、45 m，共39 936个单元以及41 386个节点。位移边界设置：对模型的底面施加竖向约束，侧面施加水平向约束，模型顶面为自由面。

2.2 计算过程

(1)进行既有隧道的建模计算。包括既有隧道结构，如管片等的建立，然后对于土体进行参数赋值，进行初始平衡计算，以使土体形成自重应力场。

(2)利用土体损失计算新建隧道边界产生的收敛位移。在本案例中，下部新建隧道为平行、等直径的双隧道，同时其所处地层环境、开挖工况相似，因此为了简化计算，将新建隧道各取0.75%的土体损失率。将土体损失率代入式(6)中求得间隙参数g，下方两隧道的g值均为23.6 mm，然后针对4种不同的隧道收敛模式计算出各自隧道边界的位移。

(3)对新建隧道使用位移控制方法。根据步骤(2)中求出的两新建隧道边界各点收敛位移，对新建隧道边界进行位移控制，使下部两隧道逐步收敛到预定的收敛边界。为了使计算结果更加精确，通过8 000计算步将隧道逐步收敛至既定形状。

(4)计算结束，提取既有隧道拱底变形和地表变形。

2.3 地表沉降结果分析

图5、图6给出了A、B两个典型截面(图4)处的地表沉降量，其中A、B截面分别穿过两个既有隧道中线。数值模拟的结果与实测数据进行了比较，同时在图5、图6中也给出了Yin等[19]使用力控制有限元法得出的A、B截面处的地表沉降曲线。实测与模拟结果显示，A、B截面处地表沉降的最大值都出现在新建双隧道对称中心位置，其中A、B截面处实测的地表沉降最大值分别为17.3 mm和15.5 mm。文献[19]采用力控制有限元法得出的地表沉降的最大值分别为18.3 mm和19.0 mm，误差率分别为5.78%和22.58%；而采用本文方法得出的地表沉降最大值分别为16.07 mm和16.07 mm，误差率分别为7.11%和3.68%。

图5 A截面地表沉降数值模拟结果与实测对比Figure 5 Comparison of numerical simulation results and measuring data of surface settlement on cross section A

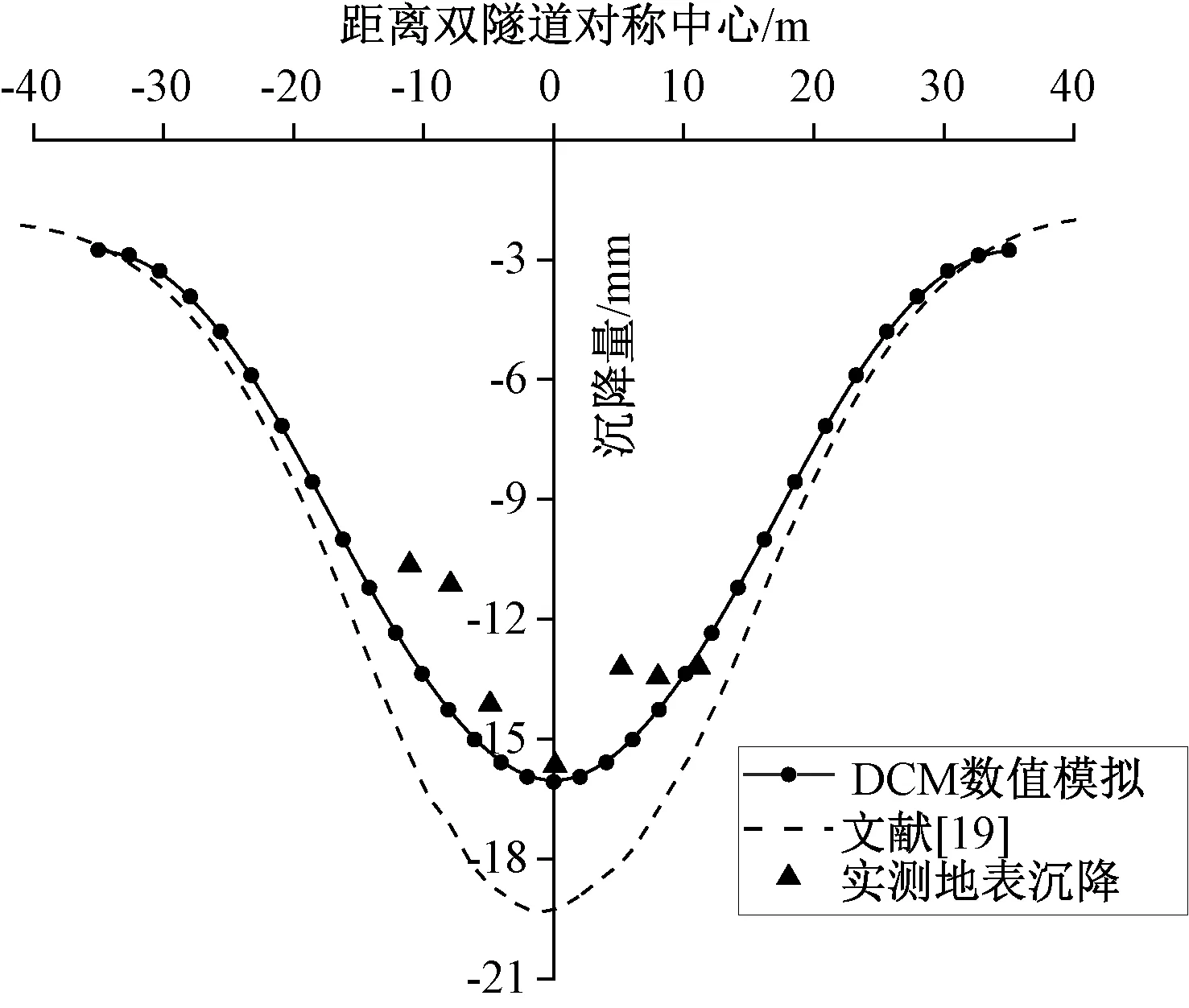
图6 B截面地表沉降数值模拟结果与实测对比Figure 6 Comparison of numerical simulation results and measuring data of surface settlement on cross section B

从图5、图6中可以看出，使用力控制有限元数值模拟得出的地表最大沉降比实测数据大，同时其得出的沉降槽也比实测数据得到的“宽”；而使用DCM法对于沉降槽宽度的预测比力控制有限元法更“窄”，且更符合实际。使用位移控制方法得出的地表沉降槽更加接近实测数据。

从与实际数据和文献[19]的结果对比来看，本文所采用的方法能够更加准确地反映新建隧道开挖引起的土体位移关系，验证了使用位移控制方法在研究双隧道下穿问题时的合理性，可以采用该模型对其他变量进行进一步的研究。

2.4 基于Park的收敛模式的地表沉降对比分析

在既有数据条件下，针对A、B两个典型截面的地表沉降，进一步研究了双隧道开挖情况下Park不同收敛模式对地表沉降的影响，位移控制方法模拟结果如图7(a)、7(b)所示。

从图7中可以看出，在左右线采取相同收敛模式、相同土体损失的情况下，相同收敛模式的既有隧道上方的地表沉降模拟结果基本相同，且呈现出正常的高斯曲线沉降模式。无论哪种收敛模式，沉降槽均在双隧道对称中心处取得了最大值，其中BC-2得到的地表沉降最大，使用BC-3和BC-4的收敛模式得出的地表沉降较为接近且都略小于BC-2。而使用BC-1的收敛模式得出的既有隧道拱底变形则明显小于其他3种收敛模式，其沉降槽宽度明显大于其他3种收敛模式。这是由于在4种隧道变形模式中，BC-1具有最大的拱底隆起变形，进而导致沉降槽变“宽”。

2.5 基于Park的收敛模式的既有隧道拱底变形对比分析

为了进一步研究新建双隧道开挖对既有隧道的影响，利用该模型对既有隧道拱底变形进行研究。由于新建隧道的右线先于左线穿过既有隧道，因此本文先对右线隧道使用位移控制算法。

按照Park的不同收敛模式，对右线隧道使用位移控制方法进行模拟，模拟结果如图8所示。从图中可以看出，BC-2收敛模式下得到的既有隧道拱底变形大于其他3种收敛模式，BC-3与BC-4的收敛模式得出的既有隧道拱底变形较为接近，BC-1的收敛模式得出的既有隧道拱底变形最小，且沉降槽宽度最大。

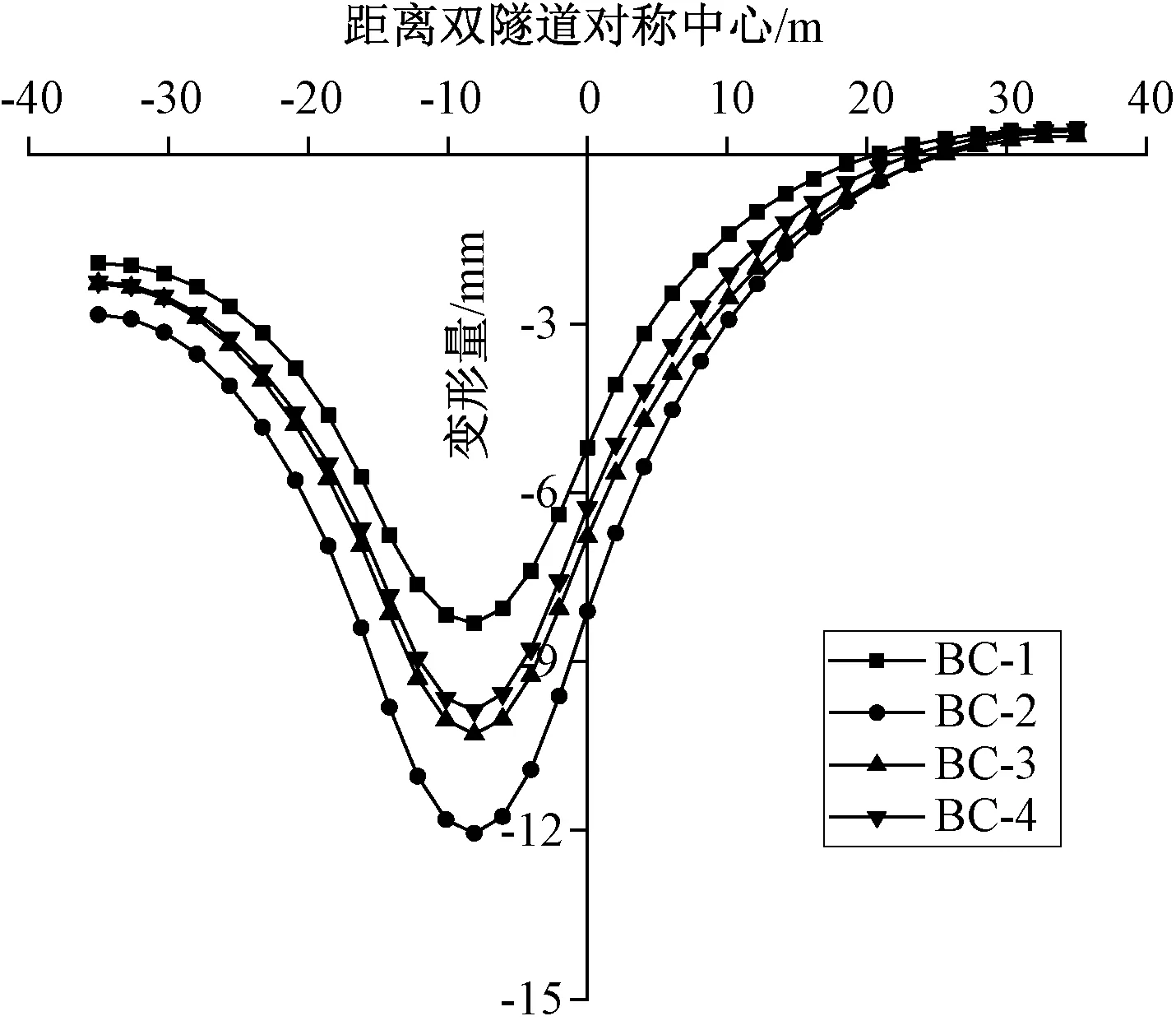
图8 单线开挖情况下Park收敛模式对既有隧道拱底纵向变形的影响Figure 8 Influence of Park convergence pattern on longitudinal deformation of arch bottom of existing tunnel under single tunnel excavation

在双隧道同时开挖的情况下，使用Park不同的收敛模式得到的既有隧道拱底变形规律如图9所示。从图中可以看出，既有隧道的拱底变形不是规整的高斯曲线，在新建双隧道对称中心上方的拱底变形相比两侧的变形较小，而在两新建隧道轴线上方附近达到最大，整体呈现一个“W”形。但BC-2依然取得了最大的拱底变形，BC-3与BC-4次之，BC-1最小。BC-3与BC-4的结果较为接近。

图9 双线开挖情况下Park收敛模式对既有隧道拱底纵向变形的影响Figure 9 Influence of Park convergence pattern on longitudinal deformation of arch bottom of existing tunnel under twin-tunnel excavation

3 讨论

本文方法中的间隙参数g值采用土体损失率计算得出，是目前使用较多的一种方法。其优点主要有：计算简便，快速高效；可以考虑各种施工方法和隧道设备配置；可以考虑土体的弹塑性性质。在以BC-1和BC-2为边界条件进行考虑时，g值的计算具有良好的数学意义，能够较为精确地描述该边界条件下g值与土体损失的关系。

但这种方法同样存在一定的局限性：首先相较于Lee等[18]提供的g值计算方法(式(7))，使用土体损失计算的g值缺乏一定的物理意义；其次，没有考虑到BC-3和BC-4特殊收敛形状对土体损失率的影响。为了简化计算，本文对4种收敛模式采用了相同的g值，从严谨的数学关系来看，此时Park的4个收敛模式所对应的实际土体损失值有较小的不同，大小关系为VBC-1=VBC-2>VBC-4>VBC-3。

观察本文对于4种收敛模式的计算结果可以看出，无论是地表沉降还是既有隧道拱底变形都存在相同的特点：新建隧道的拱底变形量对结果会产生较大影响。当采用相同的g值时，计算BC-1和BC-4由于都考虑了新建隧道拱底的隆起，因此其最大沉降都低于其他两种收敛方式；同时比较BC-3和BC-4也不难看出，在收敛模式相似的情况下，考虑隧道拱底隆起的收敛模式将取得更小的地表沉降或既有隧道拱底变形。

4 结论

(1)本文所采用的计算方法简化了对隧道支护压力的复杂计算程序，仅需要计算间隙参数，更为简单、更容易控制，同时证明：采用Park收敛模式克服了力控制法计算造成的地层沉降槽较“宽”的缺点。

(2)Park收敛模式中，BC-2模式与实测结果最为接近，也最为简单，均匀收敛BC-1模式结果偏小。

(3)隧道正交下穿既有隧道导致的地表沉降与地层中既有隧道变形模式可能不同，当隧道间距一定时，地表沉降为高斯曲线，而隧道变形可能表现为“W”形。

(4)收敛模式相似的情况下，考虑隧道拱底隆起的收敛模式将取得更小的地表沉降或既有隧道拱底变形。