基于非零和信号博弈的主动防御模型

黄万伟， 袁 博， 王苏南， 张校辉

(1.郑州轻工业大学 软件学院，河南 郑州 450001； 2.深圳职业技术学院 电子与通信工程学院，广东 深圳 518005； 3.河南信安通信技术股份有限公司，河南 郑州 450001)

0 引言

在过去几年里，以高级持续性威胁(advanced persistent threat, APT)为代表的网络攻击对网络信息安全造成了严重的威胁，国家和企业面临着严峻的考验[1-2]。APT攻击带有明确的目的性，攻击方式复杂多变，对目标系统实施有计划、全方位的入侵，以达到最终目的[3]。传统的被动防御技术只能在破坏活动发生后采取降低破坏程度的补救措施，无法应对当前愈来愈灵活的APT攻击[4]，因此，亟须一种有一定预测能力的主动防御方法，在APT造成重大损失之前将损失降到最低。

主动防御技术具有灵活多变的特点，是解决当前网络安全问题的有效方法之一[5]，其中应用于主动防御技术中的博弈论是解决APT问题的有效指导理论[6]。博弈建模需要解决两个问题[7]：如何准确描述攻防双方的策略选择和行动顺序；如何对攻防过程进行量化。针对以上问题，研究者已经做出了一些研究。孙文君等[8]提出一种基于FlipIt模型的攻防博弈模型；Fang等[9]提出了一种面向APT的攻击路径预测模型，能在一定程度上预测下一步攻击行动。但以上博弈过程是在信息可靠的基础上提出来的，在实际应用过程中有很大的局限性。姜伟等[10]提出了攻防策略分类及其成本量化方法，随后在文献[11]中构建了非合作两角色零和随机博弈模型，然而在攻防收益量化的过程中采用零和方法[12]，并不符合实际攻防情况。针对零和方法存在的问题，孙骞等[13]和李静轩等[14]构建了基于非零和的博弈模型，并给出了策略选取方法，而该方法没有考虑到双方信息不完全对称的问题。Yang[15]提出基于攻防信号的博弈模型，在建模时选择攻击者作为信号的释放者，但实际攻防过程中防御者很难获取该信号，缺乏可行性。针对文献[15]存在的问题，张恒巍等[16-17]建立了基于信号博弈的主动防御模型，并选取了防御方作为信号的释放者。同时，张为等[18]从防御角度构建博弈模型，在一定程度上可以增强系统的防御能力，却不能很好地体现出多阶段信号博弈的收益。

针对上述问题，本文基于信号博弈理论与非零和思想提出了一种基于非零和信号博弈的主动防御模型，选择防御者作为信号的释放者，通过释放混合信号来提高防御能力，提出了贴现因子来对多阶段收益的情况进行量化描述，通过求解当前最优策略算法得出本阶段最优防御策略。

1 非零和信号博弈模型

1.1 攻防博弈过程分析

网络安全包括3个主题：攻击者、网络系统和合法用户。合法用户只是获得网络系统的服务[19]，因此本文主要考虑攻击者和网络系统间的信号博弈。在APT信号博弈过程中，首先由防御者释放信号，由于防御者的信息影响着攻击者的决策，因此防御者释放夹杂虚假信息的信号可以增加攻击者的攻击代价，并根据已知的攻击方式构建防御策略。攻击者在攻击前会先对目标系统进行检测，收集目标在外网中的详细信息以及防御方发出的信号，找到目标系统防御的薄弱点，生成先验概率集合，根据接收到的信号，遵循贝叶斯法则生成后验概率集合，并选择攻击策略。在下一阶段，防御者根据所预测的攻击者的攻击构建防御策略，并继续释放夹杂虚假信息的信号，攻击者根据收到的信号生成新的后验概率集合，并选择攻击策略。后面阶段的攻防过程以此类推。多阶段对抗过程如图1所示。

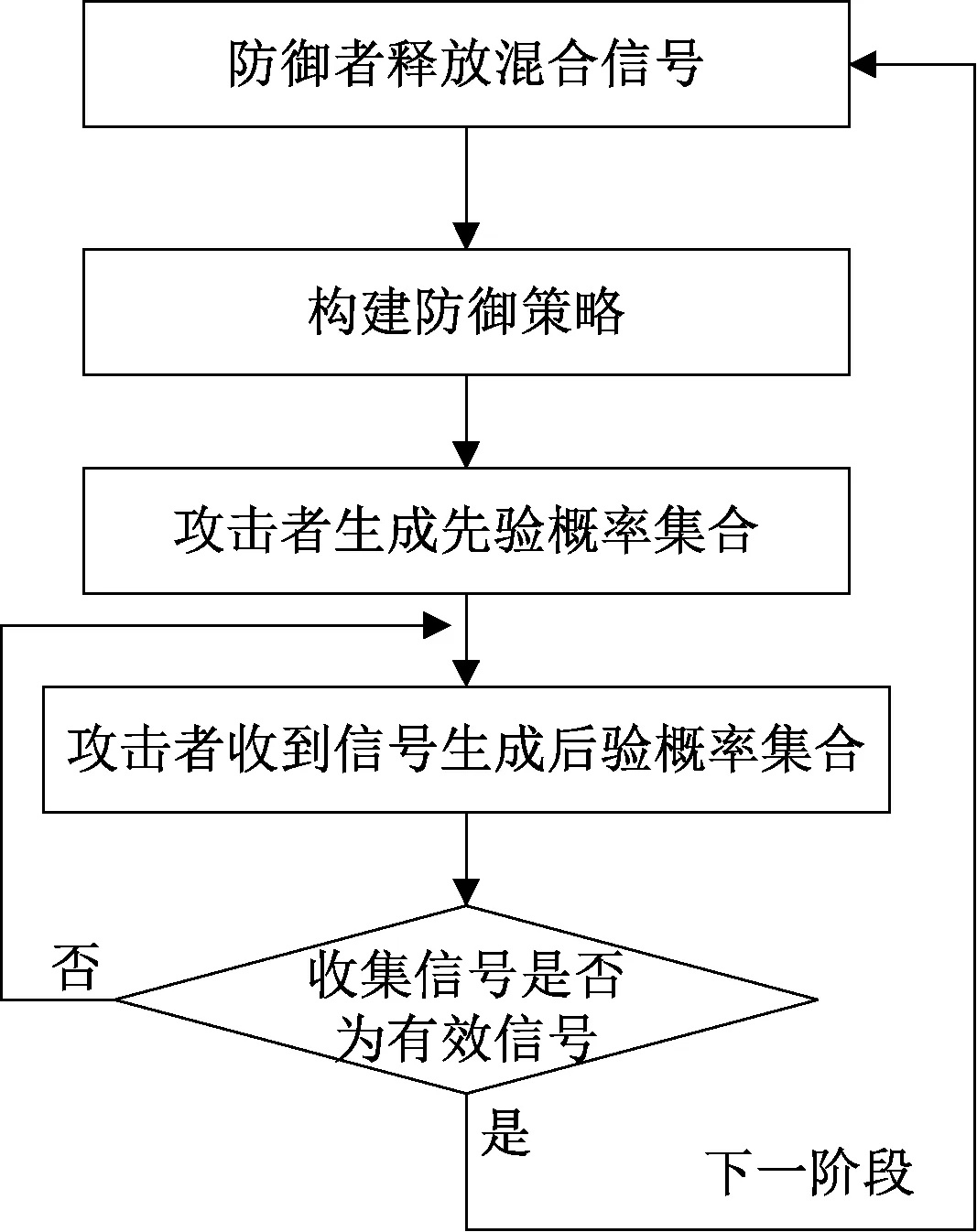
图1 多阶段对抗过程Figure 1 Multistage confrontation process

根据以上叙述，将其所释放的夹杂虚假信息的信号定义为混合信号。借鉴信号博弈的基本理论，其对抗过程是一个多阶段策略选择不断变化的过程：攻防双方在每阶段都会从对方释放的信号中来预测出对方在下一阶段采取的行动，并从己方最大利益出发选择最优策略，其攻防博弈树如图2所示。

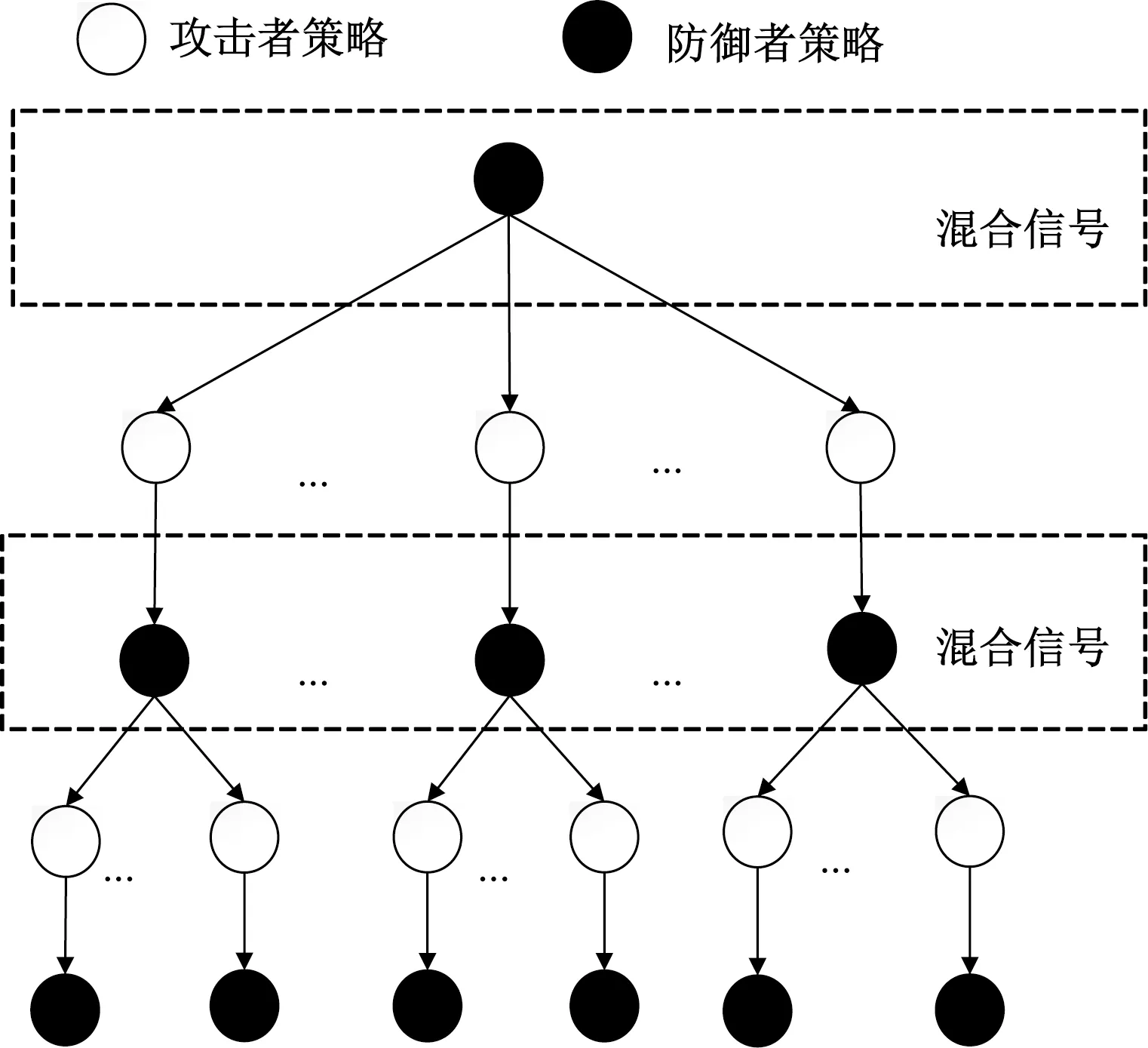
图2 攻防博弈树Figure 2 Attack and defense game tree

从以上分析可以得出，双方当前的策略选择主要与上一时刻双方所释放的信号有关，其状态转移具有一定的Markov性。

1.2 模型的假设

通过分析网络攻防过程，本模型假设如下。

假设1利益最大化假设，即博弈参与双方所选择的策略都是基于实现自身收益最大化，其策略选择受其操作代价和实际条件的影响。

假设2状态有限性假设，即APT攻防过程的步骤是有限的，因为攻防双方对资源的消耗是不可逆的，双方不可能无休止地进行行动，因此整个博弈过程不存在死锁现象。

假设3信息可知性假设，即攻防双方基本了解对方可能进行的行动手段及其相应结果。APT攻击是过去攻击的结合，而不是新的攻击[9]，所以防御方会对攻击者可能采取的攻击行为及其结果有大概了解，而攻击者同样会对防御者可能采取的防御行为及结果基本了解。

1.3 模型的定义

基于上述3个假设，定义非零和信号博弈模型NSG=(N,S,θ,ω,M,P,C,R,τ,U)，其中：

(1)参与者空间N={ND,NA}。ND代表防御者，NA代表攻击者，多阶段网络攻防过程也可以看作是两者之间的博弈过程。

(2)状态空间S={S1,S2, …,St|t∈N+}。每个状态都是表示在上一阶段双方博弈后系统所处的状态，该状态只与上一状态双方选择的策略有关。

(3)类型空间θ。θ所代表的是防御者的类型空间，其现实意义是代表防御者的资源类型，按照防御能力可分为多种类型，即θ={θ1,θ2,…,θn|n∈N+}。

(4)攻防策略空间ω{D,A}。防御者的策略空间为D={D1,D2,…,Di}，其中Di表示某一防御策略，为防御动作的集合Di={d1,d2,…,dm|m∈N+}，dm表示某一具体的防御动作；同理，攻击者的策略空间为A={A1,A2,…,Aj}，其中Aj={a1,a2,…,an|n∈N+}，an表示某一具体的攻击动作。

(5)信号空间M={m1,m2,…,mk|k∈N+}。信号空间是所有信号的集合，其中包含着真实信号和伪装信号，设k为防御者释放的信号数量，当k=1时，代表释放的为真实信号，当k=2时代表为1个真实信号和1个伪装信号的混合信号，当k=3时表示为1个真实信号和2个伪装信号的混合信号，k=4，5，…，以此类推。

(6)概率P，0 ≤P≤ 1。P(mk)为释放信号mk的概率，其值是由攻击者在收集目标系统的信息时确定的。P(Aj)表示攻击方采用策略Aj的概率，其值与释放信号的概率有关，根据贝叶斯法则可以得出下式[18]:

(1)

P(Di)表示防御方采用Di的概率，其值与攻击者采取的攻击策略的概率有关，根据贝叶斯法则可以得出以下公式:

(2)

P(Di,Aj)表示防御者采用防御策略Di，攻击者采用攻击策略Aj后，攻击者攻击成功的概率。设防御者释放的混合信号量为k，因此攻击者命中真实信号的概率为1/k，根据假设条件3，防御者针对攻击策略Aj选择防御策略Di的概率为PD(Di)，所以针对该攻击防御失败的概率即为1-PD(Di)，可得出攻击者攻击成功概率为

P(Di,Aj)=∑PA(Aj)(1/k)·(1-PD(Di))。

(3)

(7)代价C。CD表示防御代价，CA表示攻击代价，Cm表示释放信号的代价。同文献[11]的方法，防御代价CD的求解过程如式(4)所示：

CD=Ocost+Ncost+Rcost。

(4)

式中：Ocost为操作代价，代表执行该防御策略所付出的代价；Ncost为负面代价，代表执行该防御策略导致提供的服务质量下降等带来的损失；Rcost为残余损失，代表执行该防御策略后攻击者对系统造成的未被消除的损失。

(8)即时收益R。RD表示防御者获得的即时收益，RA表示攻击者的即时收益。其中，RD(Di,Aj)+RA(Di,Aj)≠0，该公式表示在防御者采取防御策略Di和攻击者采取攻击策略Aj时所获得的即时收益之和，其值不为零，此处体验了博弈论中非零和的思想，也更符合网络攻防实际收益情况。

防御者的即时收益RD(Di,Aj)可由式(5)来表示：

RD(Di,Aj)=V·AL·(1-P(Di,Aj))-

∑CD-kCm。

(5)

式中：V表示资源的价值；AL表示该资源对于系统的重要程度；1-P(Di,Aj)表示防御成功的概率；∑CD代表执行防御策略时的防御代价。

攻击者的即时收益RA(Di,Aj)可由式(6)来表示：

RA(Di,Aj)=V·AL·P(Di,Aj)-∑CA。

(6)

式中：P(Di,Aj)为攻击成功的概率；∑CA为执行攻击策略时的攻击代价。

(9)贴现因子τ，0 ≤τ≤ 1，表示先前阶段收益对之后收益的影响，此处体现了多阶段博弈的收益情况。

(10)收益函数U=(UD,UA)，为即时收益与以往阶段收益之和。UD所代表的是防御者的收益，由式(7)来表示；UA所代表的是攻击者的收益，由式(8)来表示。

(7)

(8)

2 策略求解

2.1 均衡分析

根据1.2节中的假设条件，攻击者和防御者采取的策略都是保证自身利益的最大化，攻防双方存在以下均衡。

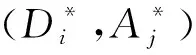
(2)精炼贝叶斯均衡。攻击者通过对防御者释放信号的收集，对信号空间M={m1,m2,…,mk}和防御策略空间D={d1,d2,…,di}进行分析，得到后验概率集合PA(Aj|mt)，经过计算总能得到最优策略A*以满足条件A*∈maxUA(D,A)，对于防御者来说同理可以得到最优策略D*使得D*∈maxUA(D,A*)。

2.2 求解当前最优策略

通过上述模型的描述以及对存在均衡解的分析，设计了一个求解当前最优防御策略的算法，如下所示。

算法1当前最优策略算法。

输入: 非零和信号模型NSG、V、AL；

输出: 当前最优防御策略D*。

①Initialize(N,S,θ,ω,M,P,C,R,τ,U);

②Initializeθ={θ1,θ2,…,θn};

③InitializeD={d1,d2,…,di},A={a1,a2,…,aj};

④InitializeM={m1,m2,…,mk};

⑤InitializePm={P(m1),P(m2),…,P(mk)};

⑥WhileSt∈Sandmk∈M

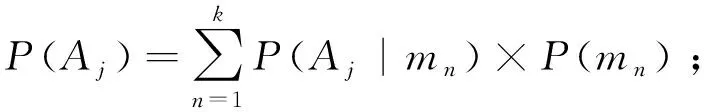
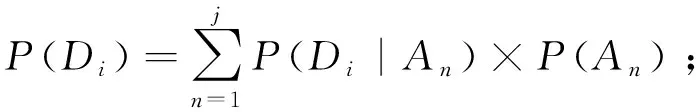
⑨Foreachdi∈Dandmk∈M

⑩RD(Di,Aj)=V×AL×(1-P(Di,Aj))-∑CD-kCm;

根据1.1节描述的博弈过程和2.1节中对两个均衡的分析，可以得出该算法的复杂度主要在于计算攻防策略的后验概率以及精炼贝叶斯的过程，其时间复杂度为O(N2)，其空间复杂度主要是用于存储各策略收益和求解的中间结果，其空间复杂度为O(mn)，与其他文献的模型对比如表1所示。

表1 算法对比分析Table 1 Comparative analysis of algorithms

3 模型验证与分析

3.1 实验环境

为了模型的可行性和有效性，本文按照典型的信息系统进行仿真，采用了如图3所示的网络拓扑结构来模拟攻防情景。攻击者想要获取目标的私密信息，首先在发动攻击前对目标系统暴露在外网的信息进行收集分析，例如目标IP地址的范围、域名以及对外网提供的应用服务等。通过收集信息，攻击者确定其防御薄弱点以及攻击方法。

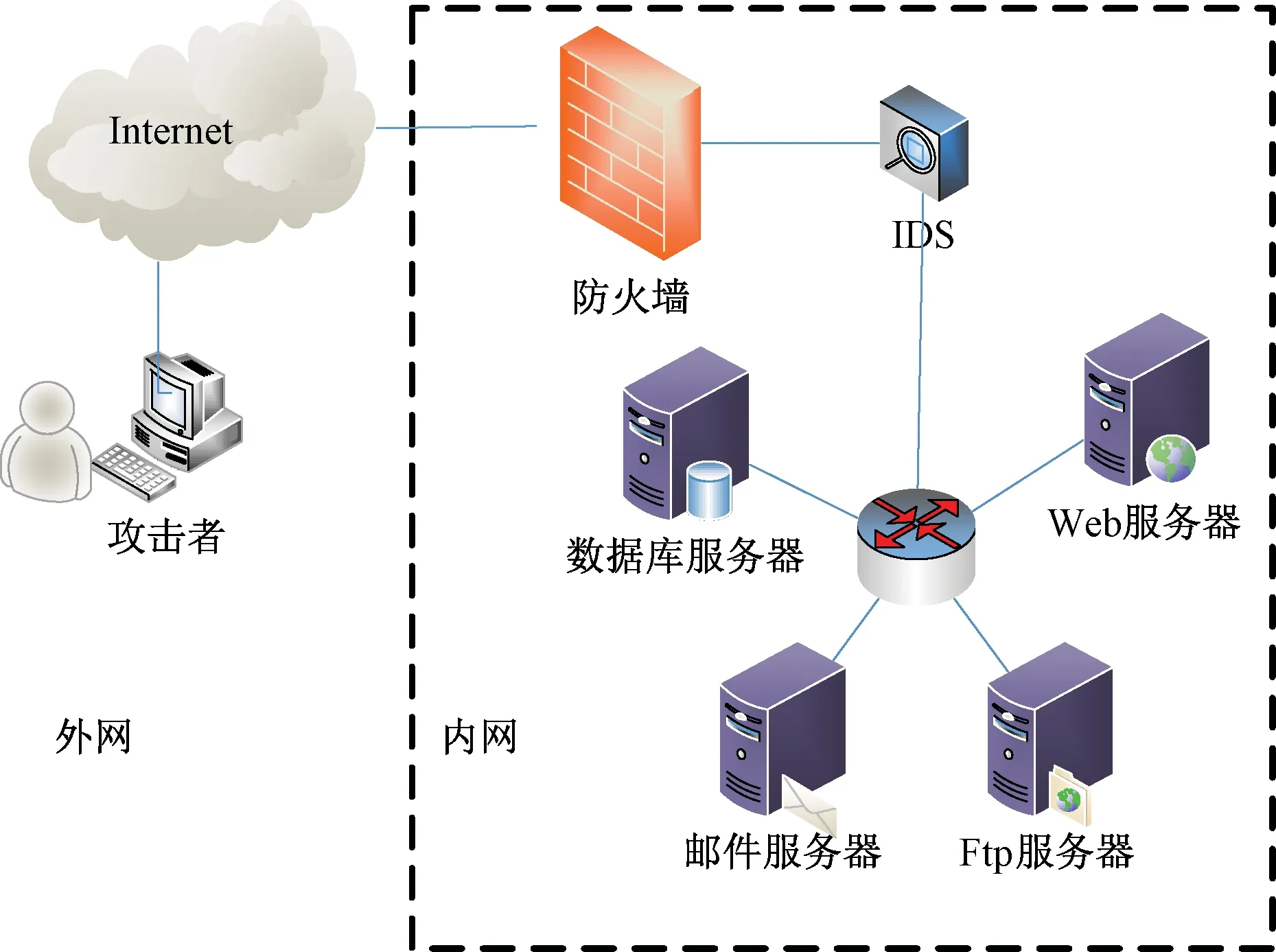
图3 攻防网络拓扑图Figure 3 Attack and defense network topology

在此次实验中，攻击者处于外部网络，目标网络由入侵检测设备、Web服务器集群、数据库服务器、邮件服务器和Ftp服务器组成，其访问规则如表2所示。根据文献[20]给出模拟实验网络脆弱性信息如表3所示。根据其脆弱性进行攻击，将AL分为10个等级，数值越大表示行为越严重，表4列出了进行该攻击的AL和攻击代价。针对存在的漏洞可以进行相应的防御动作，假设残余损失为0，其操作代价及其负面代价如表5所示。

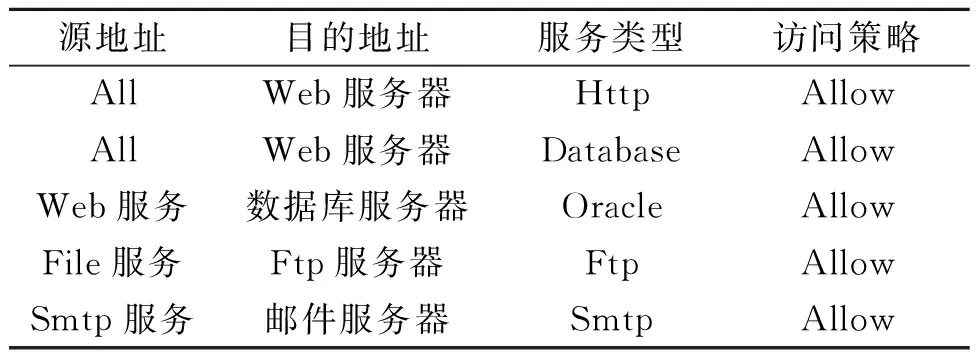
表2 防火墙规则Table 2 Firewall rules

表3 仿真实验网络脆弱性信息Table 3 Vulnerability information of simulation experiment network

表4 攻击动作和代价Table 4 Attack actions and cost

表5 防御动作和代价Table 5 Defense actions and cost

3.2 实验分析

在本实验中，预设数据的总价值V=1 000，贴现因子τ=0.3，释放信号的代价为Cm=40，根据对近年来APT案例结合以上列出的网络拓扑结构的网络漏洞进行分析，得到攻击者可能进行的攻击策略。为了简化实验过程，本实验只给出单阶段和两阶段的过程，多阶段情况以此类推。

根据文献[20]中所给出的方法对输入的路由器、漏洞数据、防火墙和防御策略进行建模和分析，得到可能采用的攻击策略A1={a1,a3},A2={a2,a6},A3={a4,a5}，根据以上假设采用对应的防御策略为D1={d1,d3},D2={d2,d6},D3={d4,d6}。

实例1博弈开始时，防御方率先发出信号，其概率为 (P(m1),P(m2),P(m3))=(0.2,0.4,0.4)，通过式(1)可以计算得到攻击者采用的攻击策略为(P(A1),P(A2),P(A3)) = (0.4, 0.3, 0.3)；采用的防御策略通过式(2)可以得到防御策略概率为(P(D1),P(D2),P(D3)) = (0.4, 0.3, 0.3)。

实例2博弈开始时，由防御方率先发出信号，其概率为(P(m1),P(m2),P(m3))=(0.3,0.35,0.35)，通过式(1)可以计算得到攻击者采用的攻击策略为(P(A1),P(A2),P(A3)) = (0.35, 0.2, 0.45)；采用的防御策略通过式(2)可以得到防御策略概率为(P(D1),P(D2),P(D3)) = (0.35, 0.2, 0.45)。

实例3博弈开始时，由防御方率先发出信号，其概率为(P(m1),P(m2),P(m3))=(0.5,0.3,0.2)，通过式(1)可以计算得到攻击者采用的攻击策略为(P(A1),P(A2),P(A3))=(0.25,0.4,0.35)；采用的防御策略通过式(2)可以得到防御策略概率为(P(D1),P(D2),P(D3))=(0.25,0.4,0.35)。

图4(a)表示随着混合信号数量k的增加，各实例单阶段攻击策略收益的变化。从中可以看到，随着释放信号量k值的增加，3个实例的攻击策略收益都是呈现下降趋势。当k=1时，即释放的信号均为真实信号时，3个实例的攻击方的收益均达到最大；当k=3时，实例1和实例2攻击策略收益趋近于0；当k>3时，实例1和实例2攻击策略收益均小于0；当k=4时，实例3攻击策略收益趋近于0；当k>4时，实例3的收益小于0；当k>12时，实例1的攻击策略收益开始小于实例2。图4(b)表示随着混合信号数量k的增加，各实例单阶段防御策略收益的变化。从图4中可以看到，随着释放信号量k值的增加，3个实例的防御策略收益趋势均为先增加后减少。当k=3时，实例1和实例2的防御策略收益达到最大值；当k>3时，实例1和实例2的防御策略收益开始减少；当k=4时，实例3的防御策略收益达到最大值；当k>4时，实例3的防御策略收益开始减少。

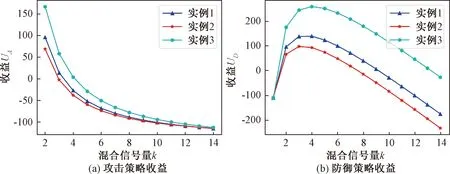
图4 单阶段策略收益图Figure 4 Single-stage strategy gains

图5(a)和图5(b)分别表示随着混合信号数量k的增加，各实例两阶段攻击策略和防御策略收益的变化。从图中可以看出，两阶段攻防策略收益分布情况类似于单阶段，两阶段收益=第2阶段的即时收益+第1阶段收益×贴现因子。通过对比单阶段和两阶段的攻防收益图能够体现出本文所提出的多阶段收益量化思想。

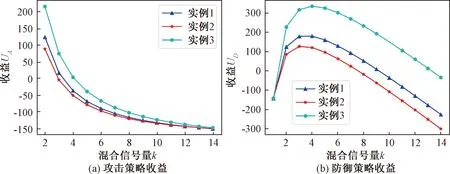
图5 两阶段策略收益图Figure 5 Two-stage strategy gains

4 结论

本文以典型的信息系统进行网络攻防仿真实验，分析实验结果得出以下结论：①混合信号的数量与攻击者的收益有着负相关的联系；②防御方不断增加混合信号数量，不一定能获得较高的安全增益；③网络攻防存在着攻防收益的不对称。

本文基于攻防信号博弈理论并结合了博弈理论中非零和的思想，在3个假设条件的基础上，将攻防双方的博弈过程进行建模，将攻防策略收益进行量化，根据多阶段信号博弈过程中收益情况引入贴现因子，并通过仿真实例验证了本文所提模型和方法的有效性。