基于变指数滑模的双馈水电机组功率控制研究

林增健 刘文泽 谭炜豪

(华南理工大学 电力学院, 广州 510640)

双馈发电系统与传统的同步机发电系统相比,具有显著的优势.双馈发电机机组通过调节变流器提供的交流励磁电流的频率,可以实现机组的变速恒频运行.由于双馈发电机组具有变速恒频运行的特点,因此特别适用于风电、水电这种动力源随时间变化较大的发电机组[1].风电、水电的随机性、波动性较大,使得机组往往不在理想工况下运行,且运行工况变化频繁.同步运行时,机组只能运行在同步转速下,运行工况偏离理想工况,会造成效率降低、机组损坏等不良影响.双馈发电机系统利用变速恒频特性,则可根据运行工况调整转速,使机组运行在最优转速下,实现最大功率点追踪,提高功率,优化运行工况[2].因此,双馈发电系统在水电、风电方面有较多应用研究[3-8].

双馈水电机组的适用范围较广,引水式水电站、径流式水电站、抽水蓄能水电站等均可采用双馈水电机组.目前水电站机组多采用同步运行方式.双馈水电机组的优势在于与同步机组相比,在变工况情况下能调节转速,实现更大出力.所有的水电机组都会受水力资源的影响,水头高度、水流流速、压力等在一年中会有一定波动变化,从理论上说,双馈水电机组适用于所有水电站,要充分发挥双馈水电机组的变速运行优势,则可以应用在工况变化较大的水电机组,如抽水蓄能水电站.

双馈水轮发电机系统是一个涉及水力、水轮机、双馈电机等环节的综合系统[9].双馈水轮发电机系统在运行的时候,调速器通过检测机组转速测量值和转速给定值之间的偏差,相应地调节导叶开度.由于水流惯性,导叶开度的变化会引起进水流量的反向变化从而影响发电系统的稳定性.实际上水轮机调节是一个动态过程,参数也会随着工况运行点的不同而变化,目前大多数都是用水轮机静态模型下求取的参数来进行控制的.电液随动系统是一个具有死区、限幅特性的非线性环节,会带来不确定的干扰.双馈异步电机是一个参数时变、强耦合的非线性系统,具体参数不仅与运行点相关,而且运行过程中的电机温升、磁路饱和、电网电压波动等都可能引起参数变化,因此要准确得到电机模型参数比较困难.

传统PI控制算法简单、易于调整,因而得到了广泛的应用.但是PI控制是针对系统在某一平衡点附近的近似线性化模型设计的,不能保证在干扰、负荷变化和运行点变化等引起参数波动变化的情况下,仍能取得较好的控制效果[10].

滑模控制可以很好地解决PI控制中出现的受干扰或参数变化影响的问题.滑模控制通过对滑动模态的设计,使系统按照滑动模态进行运动,具有设计简洁、对参数变化与扰动不灵敏、响应快速等优点,可适用于线性系统、非线性系统、连续系统、离散系统、确定性系统、不确定系统等复杂系统.由此可知,滑模控制算法也适用于复杂非线性、不确定的双馈水轮发电机系统的控制[11].但是滑模控制存在抖振现象,需要通过一些改进方式进行克服.

针对双馈水轮发电机系统,提出一种基于变指数趋近律的滑模控制策略,在进入滑模面之后,能有效削弱抖振幅度,具有响应快速、消除稳态抖振的优点.

1 双馈发电机数学模型

1.1 dq 坐标系下DFIG 的数学模型

经过Clark变换、Park变换两次坐标变换,即将双馈发电机DFIG 在三相静止坐标系下的数学模型转换到了dq同步旋转坐标系下,得到了dq坐标系下的DFIG 数学模型,见式(1)～(2)[12]:

电压方程为:

式中:usd、usq、urd、urq分别为定、转子dq轴的电压分量;isd、isq、ird、irq分别为定、转子dq轴的电流分量;ψsd、ψsq、ψrd、ψrq分别为定、转子dq轴的磁链分量;p为微分算子;Rs、Rr分别为定、转子电阻;ω1为定子磁场的同步角速度;ωs=ω1-ωr为转差角频率,其中ωr为转子角速度.

磁链方程为:

式中:Ls、Lr分别为定、转子电感;Lm为定、转子绕组间互感.

电磁转矩为:

式中:TL为水轮机提供的驱动转矩;J为机组转动惯量.

1.2 基于定子磁链定向的功率解耦控制

双馈发电机可通过调节励磁电流的幅值、相位、频率,在实现变速恒频的基础上,实现功率的控制.

在dq坐标系下DFIG 数学模型的基础上,对转子侧应用定子磁链定向的矢量控制.假设定子磁链ψs在空间中始终以同步速度ω1旋转,并且始终与d轴重合.由此可以得到定子磁链,见式(7):

双馈发电机在正常运行中,定子电阻值远小于定子电抗值,因此在此可对定子电阻进行忽略简化.将定子磁链方程(7)代入到定子电压方程(1)中可以得到定子电压:

由此可以看到,定子磁链矢量的励磁控制可以实现双馈发电机的有功和无功解耦控制,分别调节转子d、q轴励磁电流ird、irq,就可以调节双馈发电机的有功、无功输出.

2 改进后的变指数趋近律

指数趋近律为了保证在有限时间内到达滑模面,增加等速趋近项-εsgn(s).在到达滑模面后,等速趋近项使得系统仍然以ε的速度进行运动,在滑模面上来回切换,造成系统的抖振[14-16].为了改善系统的稳态性能,削弱抖振,对指数趋近律进行改进,提出了变指数趋近律:

变指数趋近律和指数趋近律的相轨迹如图1所示,虚线表示切换带.从图中可以看出,变速趋近律的切换带由经过原点的两条射线组成,相轨迹趋近于原点,且抖振逐渐减小到零.指数趋近律的相轨迹则是趋近于原点的一个抖振.因此,达到稳态时,指数趋近律的抖振由等速趋近项的增益ε决定,变指数趋近律可以实现较小的抖振甚至为零.

图1 相轨迹图

3 滑模控制器的设计

因此,可以得到输出控制量为:

因此基于变指数趋近律的积分滑模控制器设计框图如图2所示.

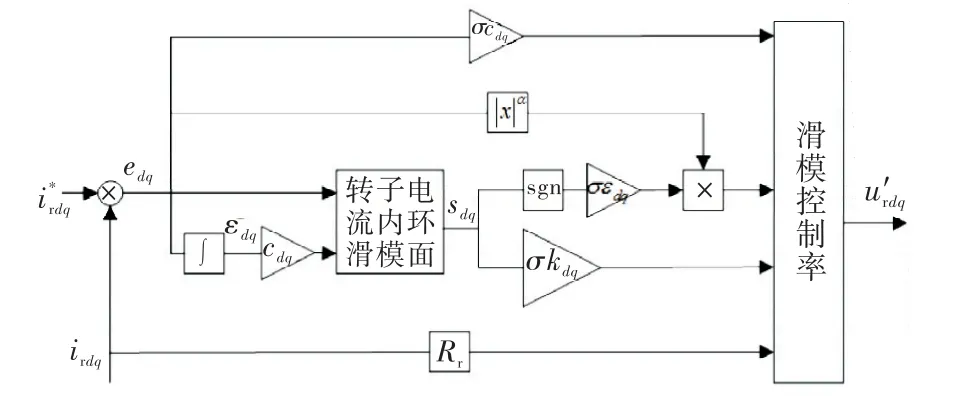
图2 基于变指数趋近律的积分滑模控制器

对该滑模控制器进行稳定性验证,取Lyapunov函数为:

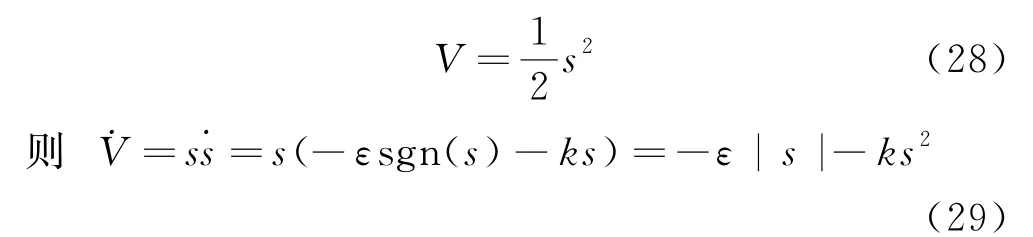
当ε,k＞0时,˙V＜0恒成立,且V=(1/2)s2为非负定.因此由稳定性理论可得,该积分滑模控制器具有稳定性,可在有限时间内达到稳态.

4 仿真及实验分析

为了验证该控制器性能的优异,搭建双馈水轮发电机组模型.转子侧励磁控制分别采用传统PI控制、指数趋近律的滑模控制、变指数趋近律的滑模控制,对比它们在变工况下有功、无功的表现.

4.1 双馈水轮发电机系统控制结构

双馈水轮发电机组由水轮机调节系统、双馈感应发电机、变流器励磁控制等部分组成,系统结构如图3所示.

图3 双馈水轮发电机系统结构

双馈感应发电机主要参数为:额定功率2.5 MW、机端额定电压900 V、基本角频率314.16 rad/s、最大转差率0.3、定子电阻0.0054 p.u.、定子电感0.1 p.u.、转子电阻0.006 07 p.u.、转子电感0.11 p.u.、互感4.5 p.u.;水轮机主要参数为:额定水头1.0 p.u.、额定出力1.0 p.u.、额定开度1.0 p.u.、额定空载流量0.05 p.u.、压力管道水头损失系数0.02 p.u.、阻尼常数0.5 p.u..

4.2 仿真结果分析

分别在有功、无功功率指令发生阶跃突变的情况下,对比传统PI、传统指数趋近律的滑模控制和变指数趋近律的滑模控制3种控制器进行有功、无功功率调节的性能.出于对比严谨性的考虑,滑模面参数应一致,指数趋近律和变指数趋近律的指数趋近项参数应一致.

PI控制器参数为Kd=1.2,Id=1.0;传统指数趋近律的滑模控制器参数为cd=4,kd=12,εd=0.5,ca=4,ka=12,εq=0.5;变指数趋近律的滑模控制参数为cd=4,kd=12,εd=1,ad=0.5,ca=4,ka=12,εq=1,aa=0.5.

4.2.1 有功功率控制

有功功率指令从0.7 p.u.改变为1.0 p.u.,保持无功功率不变,仅在有功功率指令发生阶跃变化时,对比3种控制器进行有功功率调节时的性能.图4为3种控制器控制下的有功功率变化情况.

图4 3种控制器控制下的有功功率调节过程

传统PI控制器控制下,到达目标值的时间为62.6 ms,有功功率调节过程中出现了较明显的超调量,经过2次震荡达到稳态.指数趋近律的滑模控制器的调节时间为22.9 ms,调节速度快,但出现明显的抖振现象.变指数趋近律的滑模控制器调节时间与指数趋近律大致相同,抖振现象不明显.3种控制器进行有功调节时的性能对比见表1.

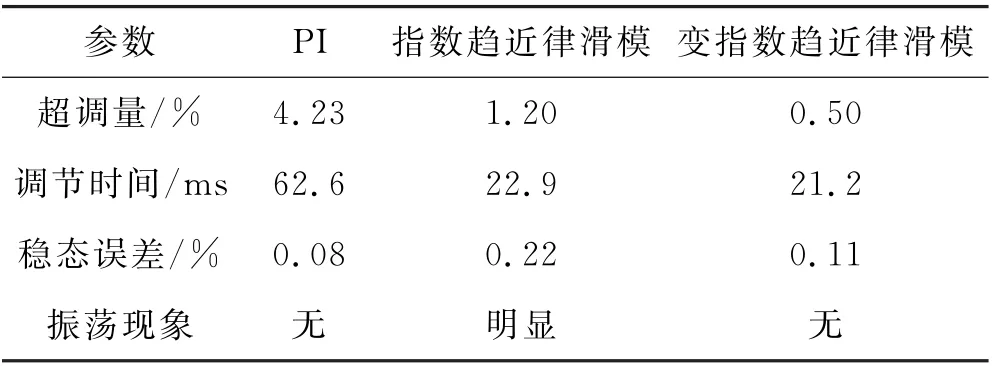
表1 3种控制器进行有功调节时的性能对比

进行有功调节,滑模控制器与PI控制器相比,在快速响应方面具有良好的性能,调节速度快,无超调量,振荡少.与指数趋近律的滑模控制器相比,变指数趋近律的滑模控制器,不仅具备滑模控制器快速响应的良好性能,在稳态时也能有效削弱抖振现象,具备良好的稳态性能.

4.2.2 无功功率控制

无功功率指令从0 p.u.改变为0.2 p.u.,保持有功功率不变,仅在无功功率发生阶跃变化时,对比3种控制进行无功功率调节时的性能.图5为3种控制器控制下的无功功率变化情况.

图5 3种控制器控制下的无功功率调节过程

传统PI控制器控制下,到达目标值的时间为188 ms,无功功率调节过程中出现了较明显的超调量,经过2次震荡达到稳态.指数趋近律的滑模控制器的调节时间为251 ms,调节时间长于PI控制器,达到稳态后仍有明显的抖振现象,存在较大的稳态误差.变指数趋近律的滑模控制器调节时间为156 ms,抖振现象逐渐减弱,达到稳态误差较小.3 种控制器进行无功调节时的性能对比见表2.

表2 3种控制器进行无功调节时的性能对比

进行无功调节,指数滑模控制器与PI控制器相比,由于振荡现象的存在,调节时间更长,并没有体现出快速响应的优势,但是减小了调节过程的超调量;稳态时也存在非常大的稳态误差.变指数趋近律的滑模控制器对振荡现象进行削弱后,具备滑模控制器的快速响应的良好性能,调节时间小于PI控制器;同时调节过程的超调量仅为0.4%,远远小于PI控制器的15.4%.在稳态时也能有效削弱抖振幅度,稳态误差与PI控制器接近,具备良好的稳态性能.

从有功、无功功率阶跃实验结果分析中可以得知:基于变指数趋近律的滑模控制器在快速响应和稳态方面都展示出了良好的性能,能对滑模控制的振荡现象进行有效抑制,调节时间更快,超调量大幅减小,稳态误差较小.基于变指数趋近律的滑模控制器进行双馈水轮发电机组的功率控制时,在快速响应性能上要优于PI控制器和基于指数趋近律的滑模控制器,在稳态性能上与PI控制器接近,因此可以实现更好的控制.

5 结 论

针对传统PI与滑模控制存在的不足,提出一种基于变指数趋近律的双馈水轮发电机系统功率解耦滑模控制器,在实现功率快速响应的同时,削弱滑模控制中的抖振现象.在指数趋近律的基础上,加入励磁电流差作为状态变量,并根据状态变量实时改变趋近律中的增益,得到改进后的变指数趋近律,以降低抖振的幅度.根据双馈水电机组系统模型与变指数趋近律进行控制器设计,并基于李雅普诺夫稳定性定理验证控制器的稳定性.通过建模仿真,进行有功、无功功率控制实验,实验结果表明:在电流内环采用基于变指数趋近律的滑模控制器进行功率解耦控制,能够实现功率调节的快速响应,超调量小,稳态性能好,有效削弱了传统滑模控制器中的抖振现象.