基于改进深度学习混合网络与小波分析的电机故障诊断方法

李志军 陈伟根 周 湶 宗起振 卢应强

(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044;2.江苏国电南自海吉科技有限公司,南京 211153)

电机作为现代工业的主要能源动力设备,在电力系统、动力系统中都发挥着不可代替的作用.如果电机发生故障,就会对电力系统造成巨大的损失.因此,对电力可靠性而言,不断优化电机故障模式诊断的方法具有重要意义[1].

近年来,机器学习算法在电机故障诊断中的应用愈加受到重视.文献[2-4]分别将小波和支持向量机相结合、支持向量机融合多传感器信号、基于神经网络的方法用于电机故障诊断,并取得了一定的效果.但这些传统浅层学习算法存在网络拓扑结构难以确定、收敛速度慢、容易陷入局部极小等问题,从而导致机器学习性能的降低与附加特征提取量的增加.与传统浅层学习算法不同,深度学习算法有多隐层结构,自上而下地对样本数据进行逐层学习并对特征量进行提取,可以更好逼近原始特征的非线性表示[5-6].深度学习理论自提出以来,被广泛应用于语音识别、目标识别、语言处理等方面,但在电机故障诊断的应用上尚不成熟[7].基于深度学习混合网络(DLHN)算法的电机诊断方法可以解决自编码网络训练准确度低,深度受限玻尔兹曼机训练效率低的问题,但仍存在网络鲁棒性有待提高,噪声对训练影响较大的问题.

针对以上问题,本文将改进的深度学习混合网络与小波分析用于电机的故障诊断中.本文提出的改进深度混合网络(IDHN)算法在传统深度学习混合网络(DLHN)算法的基础上进行了改进:为了最小化损失,降低噪声影响,将传统的自动编码器改用降噪自动编码器(DAE),从而增强鲁棒性;为了更好地重构提取输入信号的信息,将传统的受限玻尔兹曼机(RBM)层改用高斯伯努利受限玻尔兹曼机(GRMB),以此提高模型准确度.并基于实例研究,兼顾训练时间和准确度,选取了最合理的隐藏层参数与训练样本集.结果表明:与其他浅层算法与传统的深度学习网络相比,本文提出的方法能较好地提高电机故障诊断的可靠性和准确率.

1 深度学习基本模型

2006年Hinton在研究中指出:增加网络层数量可有效提高特征学习能力,采用无监督逐层训练方法可实现多隐层网络模型构建,深度学习理论自此被提出[5].输入层、多个隐藏层和输出层共同构建了深度学习模型.同时,该层中的节点是独立且互连的.其框架主要包括堆栈自动编码器(AE)模型、受限玻尔兹曼机(RBM)、深度置信网络(DBN)模型等[5-6].

1.1 自动编码器

自动编码器(AE)可以视为有相同神经元个数的输入层与输出层的3层神经网络,如图1所示.

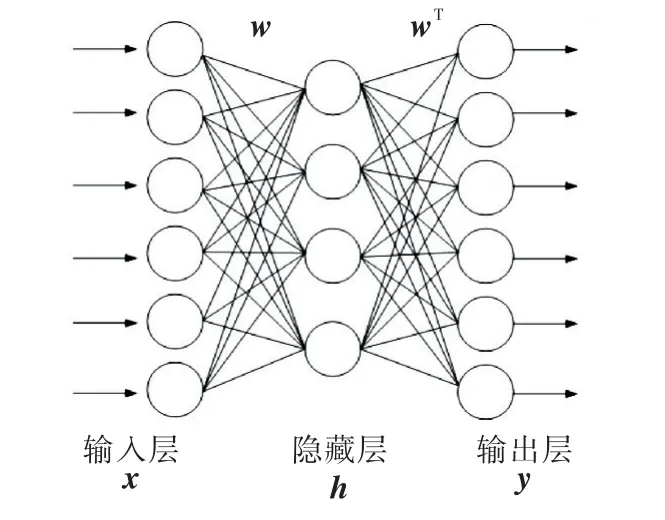
图1 自动编码器

图1中,输入层到隐含层的变换过程为编码过程;相反,隐含层到输出层的变换过程为解码过程.记f(x)和g(x)分别为编码函数和解码函数,其过程可表示为公式(1)～(2):

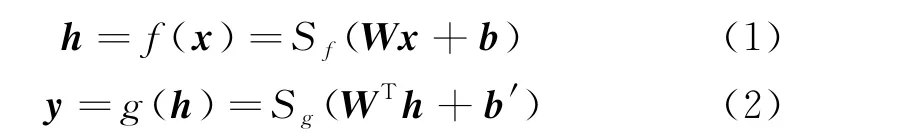
式中:S f和S g通常取为sigmoid函数;隐藏层与输入层间的权值矩阵表示为W;输出层与隐藏层间的权值矩阵表示为WT;b表示隐藏层的偏置向量;b′表示输出层的偏置向量.

编码器通过正向传导操作将原始输入转换为中间变量代码code,即原始信息的特征表示.然后将code作为解码器的输入以获得输出.利用输出和原始输入之间的残差,权重和偏差将通过梯度下降算法进行更新,直到收敛为止,从而使输出和输入尽可能接近.

1.2 受限玻尔兹曼机

受限玻尔兹曼机(RBM)是由隐性层和显性层共同构成.隐性神经元组成的隐性层用来接收输入数据,显性神经元组成的显性层用来提取高级特征.RBM 各层之间节点保持连接,层中的节点保持不连接.使用随机的1或0表示该神经元处于激活状态或非激活状态,并且该状态由能量概率统计确定.如果RBM 具有n个显式元素和m个隐藏元素,定义可见层偏置向量为a={a1,a2,…,a n},隐藏层偏置向量为b={b1,b2,…,b m},连接权重向量为w={w11,w12,…,w nm},则θ={w,a,b}可以表示RBM 的参数.

该能量函数可以表示为式(3):

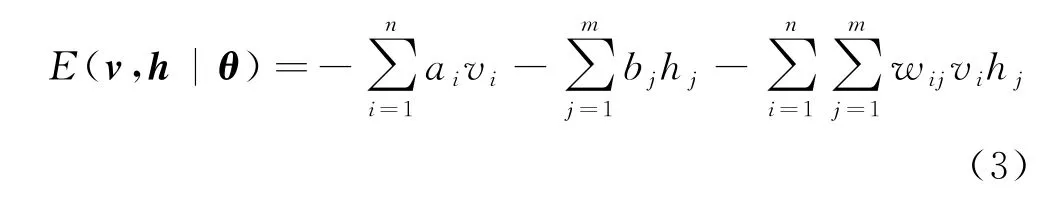
其中:v i表示第i个显元状态;a i表示第i个隐元偏置;v={v1,v2,…,v n}表示显层状态;h j表示第j个隐元状态;b j表示第j个隐元偏置;h={h1,h2,…,h n}表示隐层状态;w ij表示第i个显元与第j个隐元的连接权重.

利用能量函数求得状态(v,h)的联合概率分布,见公式(4)～(5):

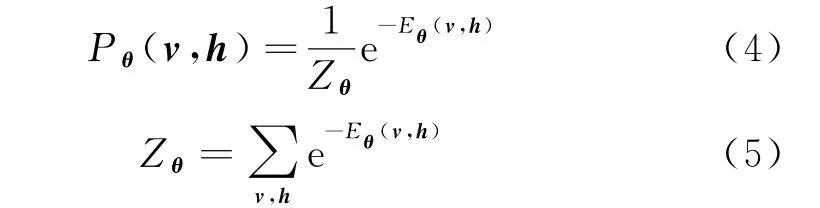
其中:Zθ为归一化因子.

RBM 结构表示如图2所示.RBM 通过极大化似然估计来逼近真实的联合概率分布,通过更新层之间的权重和神经元之间的偏差来模拟给定的训练样本.当已知可见层v的分布时,RBM 可以通过式(6)来得出隐藏层的节点概率,并进一步得到隐藏层h.

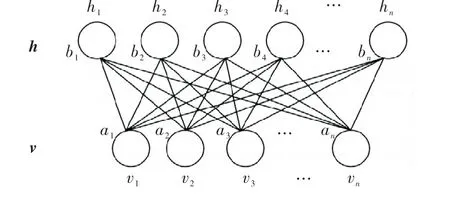
图2 受限玻尔兹曼机结构图

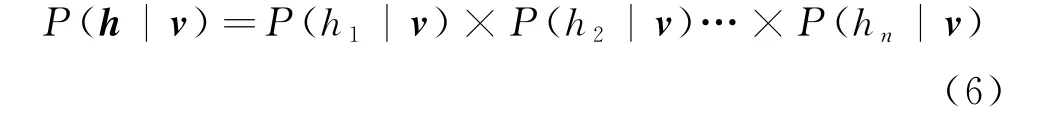
而当已知隐藏层h时,同样可以获得P(h|v),并进一步采样获得可见层v′.重复上述过程,直到v′尽可能接近v.

1.3 深度学习混合网络模型

深度学习混合网络(DLHN)由若干层AE 层和RMB层堆叠组成,并在最后添加一层Softmax输出分类层.在底层使用自动编码器以有效提高网络的训练效率,有限的玻尔兹曼机由于其自然概率生成模型而被用于中间层,分类层采用Softmax分类器.隐藏层将几个AE层和RBM 层进行堆叠混合,有效地结合了AE和RBM 的效率和高准确度,以此提高诊断性能和效率.

2 改进的深度学习混合网络模型

2.1 改进的深度学习混合网络原理

虽然深度学习混合网络(DLHN)方法可以解决自编码网络训练准确率低,深度受限玻尔兹曼机训练效率低的问题,但传统的深度学习混合网络鲁棒性有待提高,噪声对训练影响较大[7-9].为了进一步提高DLHN 在电机故障诊断中的性能与准确度,提出了改进的深度混合网络算法(IDHN).本文提出的IDHN 对传统的DLHN 进行了改进:为了最小化损失,降低噪声影响,传统的自动编码器改用降噪自动编码器(DAE),以此提高鲁棒性;为了更好地重构提取输入信号的信息,传统的RBM 层改用高斯伯努利受限玻尔兹曼机(GRMB)[10],使用概率实数值作为输入,可以更加有效地重构和复现输入信号中的有用信息,进一步降低噪声的影响和特征提取,得到良好的初始化参数,有效防止局部最优问题,以此提高模型准确度;Softmax分类器保持不变.如图3所示.

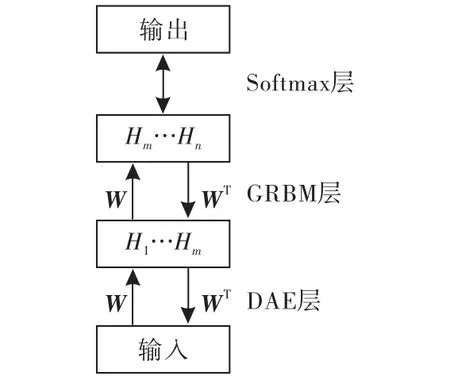
图3 改进的深度学习混合网络图

与深度学习混合网络相同,改进后的方法也通过无监督的预训练和有监督的微调来训练整个网络.在预训练中,使用去标签样本逐层训练所有DAE 和GRMB,以获得相对更好的一组初始化参数.然后使用有标签的数据进一步优化网络的参数,通过BP算法进行微调提高分类的准确性.

2.2 DAE层的训练过程

相比AE层,该模型使用DAE 的训练目标是为了降低噪声的影响,使学习的编码器有更好的鲁棒性,并提取输入样本的特征数据.训练时使用无监督的方法,让输出尽可能地复现输入数据,并使初始化参数θ更加优越.相比于上文提到的AE 层,DAE 首先将原始输入随机擦除,实际输入采用由输入向量x更改为的x′,隐藏层的压缩特征由公式(6)求得,并将原始未污染样本信息x通过式(7)进行重构,式(8)为重构后的误差公式.

其中:η为学习率;n为训练样本的数量.

2.3 GRBM 层的训练过程

相比RBM 层,IDHN 算法使用GRBM 层是为了进一步减少噪声对特征提取的影响,防止局部最优,从而提高网络的准确率.GRBM 层的训练也通过无监督的方法,输入概率实值,以便对输入信号的有用信息进行提取重构.当输入数据通过DAE 层的特征提取时,GRBM 将执行进一步的特征提取.通过公式(11),隐藏层每个节点的概率可以根据可见层v的分布进行计算,并从中得出隐藏层的分布h.然后通过公式(12)计算可见层中所有节点的概率P(h j=1|h),并对可见层v完成采样.

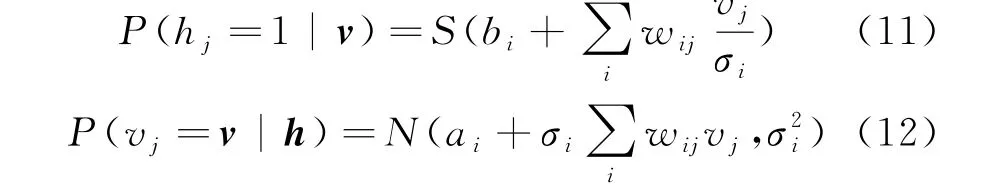
其中:S是sigmoid函数;N为正态分布函数,σ=1,为方差.

GRMB 使用对比散度算法进行训练.按公式(13)～(15)对θ更新:

其中:〈·〉data为正阶段的状态数据;〈·〉recon为重构后的模型状态分布.

3 基于IDHN 与小波分析的电机故障诊断

3.1 基于IDHN 的电机故障诊断步骤

基于IDHN 的电机故障诊断方法步骤如下:

1)对电机振动的样本数据集进行预处理归一化,并完成状态编码;

2)设置网络层数、神经元参量、学习率,初始化模型权重W、偏置向量b;

3)利用无标签数据训练第一个DAE 层,不断优化参数W与b,并将上一层输出作为下一层输入;

4)重复步骤3),逐层训练DAE 层与GRBM 等,完成模型的预训练;

5)通过反向传播算法进一步进行参数的优化,通过有标签的数据进行微调;

6)在Softmax层进行分类,对比故障诊断的输出值与标签值,识别准确率后进行保存.

流程图如图4所示.

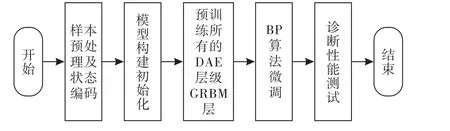
图4 基于IDHN 的电机故障诊断流程图

3.2 小波分析的特征量提取及状态编码

基于IDHN 与小波分析的电机故障诊断需要一定量的训练样本,为了避免样本单一或数据偏移,采集样本需要多个型号相同的故障电机,记录前后一段时间的正常与故障数据的振动信号.目前,输入的特征信号多采用傅里叶变换对噪声信号分析.但针对实际电机振动诊断信号中可能包含的早期微弱信号与大量的非平稳信号,传统FFT 频谱分析难以给出比较满意的结果[11-13].

本文采用小波分析的方法对振动信号提取特征参量,分别对在正常状态、转子不对中状态、轴承碰摩状态下的振动信号进行3层小波包分解.提取的小波包分解信号频率分别为S0,S1,S2,S3,S4,S5,S6,S7.原始振动信号中的最低频率记为0,最高频率记为f,S0～S7分别代表0～0.125f,0.125f～0.25f,0.25f～0.375f,0.375f～0.5f,0.5f～0.625f,0.625f～0.75f,0.75f～0.875f,0.875f～f.将频带信号总能量作为特征数据,如公式(16)所示,求各频带信号的总能量.

选取正常、转子不对中、轴承碰摩3类电机状态作为本次诊断的输出类型,采用编码法对上述故障状态进行编码,具体见表1.

表1 电机故障状态编码

3.3 基于IDHN与小波分析电机故障诊断模型的实现

基于某电厂的电机运行历史数据库,从中提取500组数据对该方法进行校验.其中训练样本数据选其中的350组,另外的150组用作测试样本数据.不同状态下的样本数据组成见表2,其中典型的样本数据见表3.

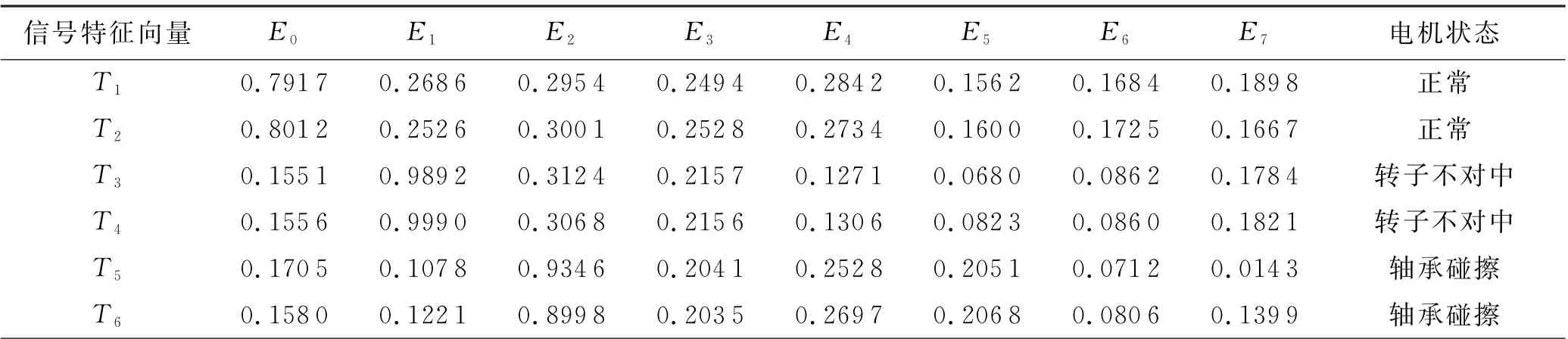
表3 电机状态典型样本数据

将经3层小波包分解后的振动信号的8个频带信号总能量作为输入,DAE 层和GRBM 层进行输入样本特征信号的处理提取,最后经Softmax层进行判别分类,输出诊断后的3种电机状态,如图5所示.

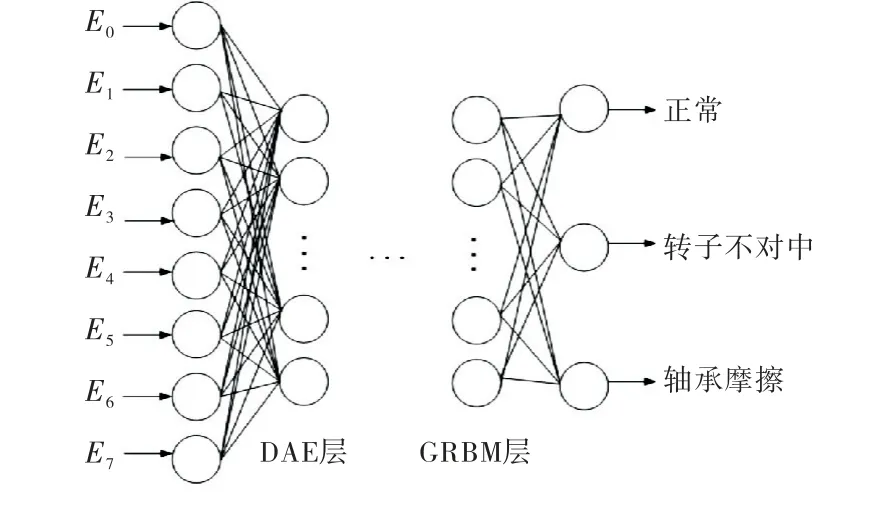
图5 基于IDHN 的电机故障诊断模型

隐藏层数目是影响收敛时间的一个重要因素,训练时间与隐藏层数目呈正相关关系,隐藏层数目越多,训练时间也将会随之增加.为了保证诊断的准确率,尽可能减少收敛时间,选择较为合理的隐藏层数目,对不同隐藏层下的诊断准确率进行了计算.基于采集的350组样本训练数据,将预训练学习速率调为0.1、迭代次数调为250次,在0～1之间随机对权重W与偏向向量进行取值,将隐藏层数目从1依次取到8,对模型进行训练后的诊断准确率如图6所示.

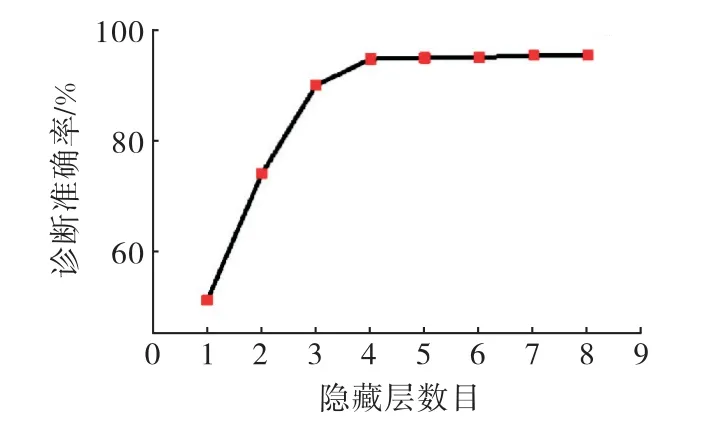
图6 不同隐藏层数目的准确率

从结果可以看出,诊断准确率随着隐藏层数目的提高是逐渐增加的.在隐藏层数目增加小于4前,诊断准确率迅速上升;当隐藏层数目大于4后,准确率趋于平稳.综合考虑到训练时间和准确率,将本次诊断模型的隐藏数目确定为4.

为了验证本方法的优越性,将本次诊断与基于向量机、BP算法、传统深度学习网络进行了比较,最终诊断结果见表4.

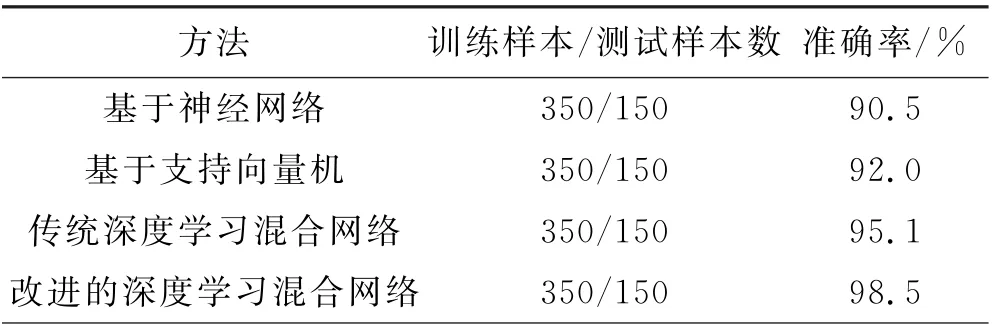
表4 不同方法的诊断结果

不同方法下不同数量样本训练后的准确率如图7所示.

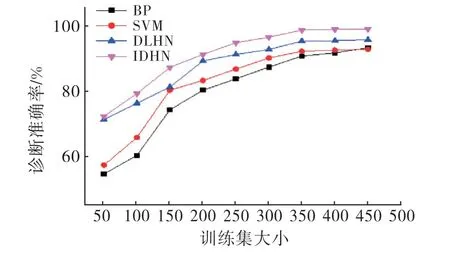
图7 不同数量样本训练后的准确率

上述比较结果表明,基于IDHN 与小波分析的诊断方法在训练集较小时就可以获得较好的性能.随着训练样本集的增加,该方法的诊断准确率基本呈上升趋势,并且当训练样本集大于350之后,其诊断准确率的增加不再明显,准确率可高达98.5%.该方法在保证诊断准确率的前提下,所需的训练样本越小,则该方法越具有可操作与可推广性.相比较浅层机器算法和传统的深度学习算法,在相同的训练样本集下,本文提出的电机故障诊断算法诊断准确率最高,具有更高的可靠性.

4 结 论

本文将深度学习混合网络与小波分析用于电机的故障诊断中,同时针对深度学习混合网络鲁棒性有待提高、噪声对训练影响较大的问题,对深度学习混合网络做出了改进,提出了一种基于改进深度学习混合网络与小波分析的电机故障诊断方法.主要结论如下:

1)基于改进的深度学习混合网络与小波分析电机故障诊断模型的隐藏层取4时,可以在保证准确率的前提下,尽量减少收敛时间.该方法在训练集较小时就有较好的性能,当训练样本大于350时,就可以获得较高的诊断准确率.

2)基于改进的深度学习混合网络与小波分析电机故障诊断方法,鲁棒性与抗噪声能力强,诊断模型构建精度较高.相比较浅层机器算法和传统的深度学习算法,可以明显地提高诊断准确率.