富水地层中锚杆加固圆形硐室围岩弹塑性分析
吴俊峰 郭剑峰 胡景波
(1.义乌工商职业技术学院,浙江 义乌 322000;2.中国电建集团华东勘测设计研究院有限公司,杭州311100;3.金华市欣生沸石开发有限公司,浙江 金华 321000)
随着地下工程的发展,处于富水区域的地下硐室开挖一直是地下工程建设中亟须解决的难题之一,地下水的影响将给地下工程的安全性和经济性造成威胁[1].在富水区域开挖硐室破坏了原始岩体的平衡状态,应力重分布改变了岩体的结构及其赋存形态,同时地下水的流动形成了渗流场,因而围岩应力场、位移场以及支护结构稳定性势必受到渗流场的影响[2].
在硐室弹塑性分析中,Mohr-Coulomb 或者Hoek-Brown屈服准则通常被采用进行硐室围岩受力与变形求解[3-4],由于它们难以反映出精确的岩石的强度特征,使得计算结果与实际情况存在较大差异.为获得更加真实的围岩应力、位移解析解,目前,学者们普遍采用统一强度理论[5],通过合理设置中间主应力系数来获得跟实际工程更为接近的强度理论,从而进行硐室围岩受力与变形求解[6-7].此外,大量实验研究与工程实际表明,岩体的变形与破坏与其剪胀扩容密切相关[8],学者们考虑了围岩剪胀扩容,推导了圆形硐室围岩应力、位移解析解和围岩塑性区半径解析公式[9-10].锚杆作为地下硐室开挖支护的重要手段,已经在地下工程中被广泛使用,研究者通过实验手段、数值模拟和理论方法认识到锚杆既能改善围岩应力状态又能提高其强度指标[11-13].富水区域的硐室开挖受到许多工程技术人员和学者的重视,他们探讨了渗流场与应力场相互作用与相互影响,研究了渗透水压、围岩软化对开挖硐室应力与位移的影响[14-15].
上述学者通过不同的研究思路建立了更接近实际工程的力学模型,并对其进行了弹塑性解答,取得了丰富的研究成果,但仍存在少许不足:大多数计算模型未涉及支护结构;仅仅把锚杆支护作用考虑成支护力,忽略了支护-围岩协调变形;较少涉及富水地层中锚杆加固硐室弹塑性分析.鉴于此,笔者在前人研究的基础上,建立了锚杆加固圆形硐室在渗流场下的力学模型,在考虑剪胀、中间主应力以及渗流等影响因素下,采用统一强度理论对开挖硐室进行弹塑性分析;继而,利用数值分析软件Flac3D 进行理论模型验证,并分析了中间主应力系数、剪胀角、渗流力对圆形硐室围岩变形和破坏的影响规律,同时也研究了对支护结构受力的影响,为富水条件下圆形硐室前期支护设计和后期围岩稳定性评价提供理论参考.
1 圆形硐室力学分析模型
1.1 力学分析模型
近年来,国内外学者对锚杆加固机理以及锚固后岩体的物理力学参数进行了研究[15],研究表明锚杆既具有通过受拉约束围岩变形,又具有通过受剪改善围岩力学特性的双重作用.学者们将锚杆支护的围岩区域定义为锚固体围岩,它有着与硐室围岩类似的物理与力学特性.不同之处在于锚杆的加固效应改善了硐室开挖后围岩的应力分布,使得围岩具有一定的径向抗拉与切向抗剪作用.硐室开挖使得围岩应力释放,围岩向着硐室中心变形,洞壁周围围岩首先进入塑性状态,随着应力释放进一步发展,塑性的围岩逐渐向外部发展.由于锚杆的加固效应,对洞壁围岩的应力释放具有一定的补偿作用,因而,锚固体围岩在硐室开挖后塑性屈服发展较慢,形成的锚固体塑性区域也相对较小.由于不同的地质环境所需要的锚杆支护强度往往不同,根据工程需要对锚杆长度与锚杆支护密度(间排距)进行选择以满足工程中硐室围岩变形控制标准.锚杆尺寸选择遵循“长而疏,短而密”原则[13].在锚杆长度的选择上可以参考传统支护理论的设计指导,再进行设计验算适当改变尺寸(长度与间排距)选择.为了计算便利,假设围岩与锚杆紧密连接、互不解耦,将锚杆接触到的圆形围岩区域视为锚固体.因此,锚杆的支护作用被考虑成作用于被锚岩体两侧的一组力p、q,此外,并认为支护后的围岩强度参数由c、φ强化为c′、φ′,力学模型如图1所示.
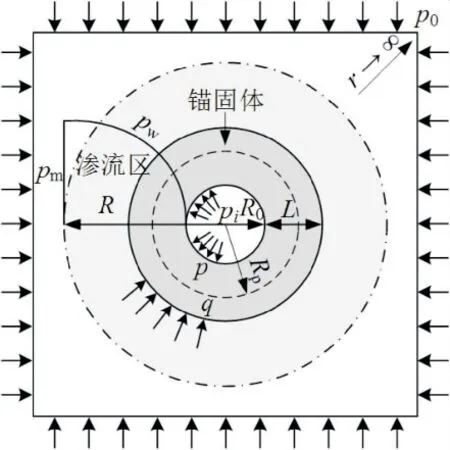
图1 力学模型
1.2 力学模型参数确定
富水地层中硐室开挖后形成的渗流场中孔隙水压力可表示如下[16]:

式中:η=1.
假设单根锚杆的影响范围为相邻锚杆距离的一半,依锚杆变形条件求得锚固体两侧的支护力为[13]:

式中:φ和φ′表示围岩与被锚围岩的内摩擦角;c和c′表示围岩与被锚围岩的黏聚力;F为锚杆轴力;α为被锚岩体主破裂面方向与最大主应力方向之间的夹角,即α=π/4-φ/2.
2 力学模型求解
2.1 塑性区应力分析
在富水地层中,考虑渗流体积力后平衡微分方程变为:

2.2 弹性区围岩应力、位移分析
由几何方程可知围岩弹性区径向和环向应变可表示为:

式中:εr和εθ分别表示围岩的径向应变与环向应变;u为围岩径向位移.物理方程为

将弹塑性边界上的应力代入屈服方程式(6)导出围岩塑性区半径Rp的解析表达式如下:
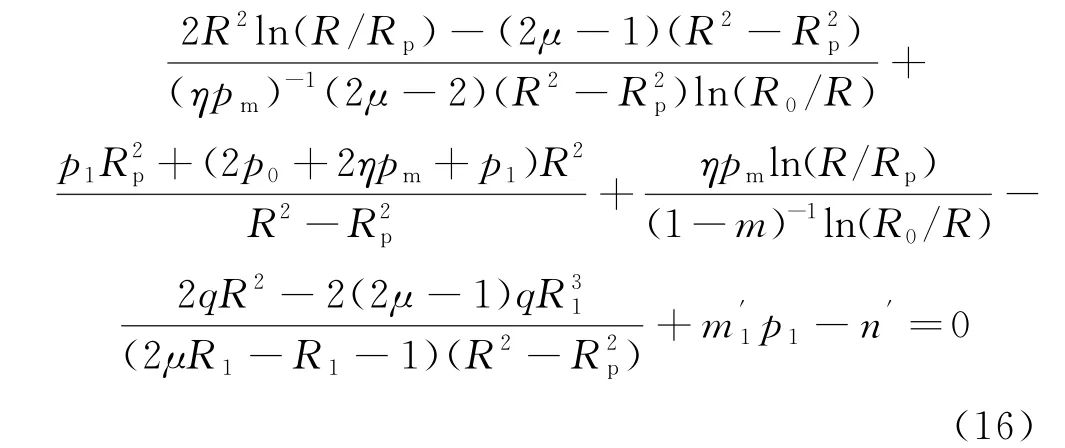
式中:R1表示锚固体外边缘所处的半径,且R1=R0+L.
在不考虑渗流、中间主应力影响以及锚杆支护时式(16)可表示为芬纳公式:
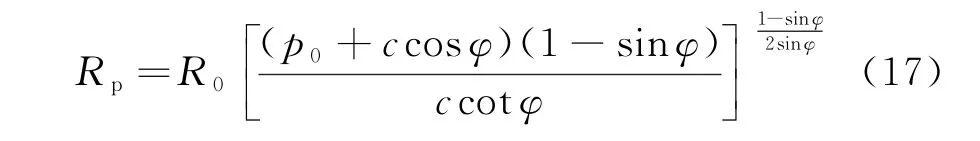
2.3 锚固体塑性区位移分析

式中:
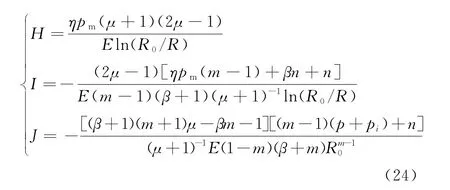
假设在锚杆与围岩协调变形过程中锚杆与围岩紧密相连、互不解耦,则锚杆伸长量Δl可由锚杆两端处围岩位移差表示,即
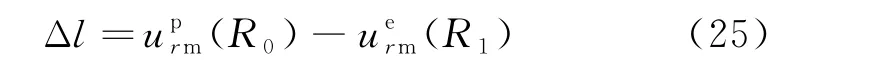
2.4 衬砌受力分析
将衬砌看作一个厚壁圆筒结构,在硐室表面围岩与衬砌的相互作用力为p i,其内外半径分别是r0和R0,如图2所示.
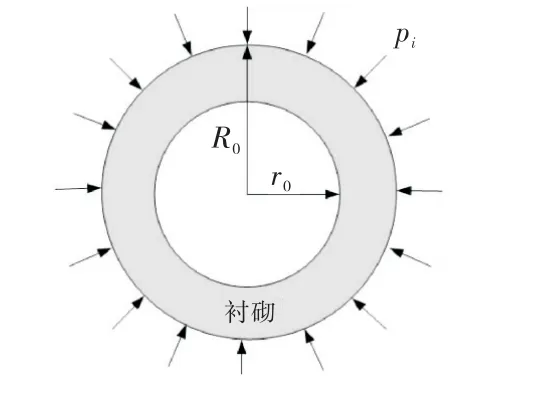
图2 衬砌力学模型
由于工程安全需要,衬砌的强度相比围岩较大,保证其变形处于弹性控制范围,因此由弹性力学可解得衬砌外边位移为:

2.5 硐室围岩稳定性评价
以硐室表面位移、锚杆轴力以及锚固体塑性程度来反映围岩的稳定性.
硐壁位移控制:

式中:[u]为硐壁允许的最大位移.
锚杆最大轴力控制:

式中:[F]为锚杆允许的最大拉力.
围岩稳定系数:
采用文献[13]中定义的围岩稳定系数k表示围岩的稳定程度,即

3 算例分析
某圆形硐室尺寸与应力状态:R0=3 m,p0=15 MPa.渗流场:pm=1 MPa;η=1;R=12R0.岩石基本力学参数:E=14 GPa;μ=0.3;c=2.4 MPa;φ=30°,锚杆支护参数:L=2.4 m;S r=0.8 m;S l=0.8 m;F0=40 k N;d b=20 mm;E b=210 GPa.衬砌力学参数:μc=0.2;E c=25 GPa.
3.1 计算模型验证
以上述算例工程为例,采用Flac3D 建立数值计算模型,进行理论计算与数值模拟计算的对比.模型本构关系采用Mohr-Coulomb准则.为了消除边界效应,数值模型尺寸设置为80 m×80 m×1 m.考虑到所分析问题的轴对称性,仅对1/4开挖硐室进行数值模型建模.在模型左侧和下边分别进行x、y轴方向的位移约束.将锚杆视为线弹性材料.由于硐室埋置较深,初始地应力在各个方向上设置为15 MPa.在12倍硐室半径范围内设置渗流场,渗流场外边缘渗流水压为1 MPa.硐室开挖后设置洞壁表面为自由透水边界.该模型由946个单元(zones)组成,其中包含2826个节点(grid-points),如图3所示.
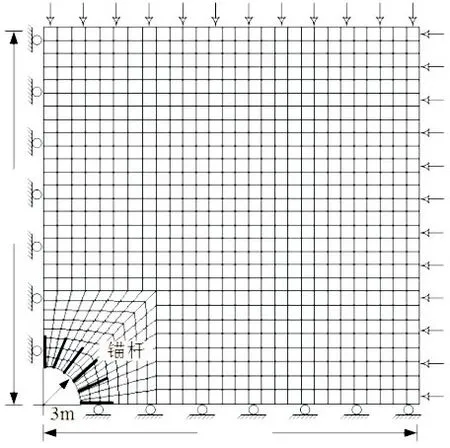
图3 数值计算模型
图4为理论解和数值模拟结果的对比曲线,可见,理论求解的围岩Rp为4.01 m,数值模拟得到的围岩Rp为3.78 m.在洞壁处,理论求得的σθ和u0分别为12.38 MPa和29.63 mm,数值模拟求得的σθ和u0分别为13.55 MPa和26.81 mm.在应力和位移分布上理论解与数值解的差异随着径向距离的增大而减小.从整体上看理论分析结果与数值模拟结果差异较小,从而验证了本文理论计算模型的合理性.

图4 计算结果对比
3.2 围岩-衬砌特征曲线分析
图5为围岩-衬砌特性曲线,可知,随着中间主应力值增大,围岩与衬砌达到协调变形时交点处支护力越小,这表明在实际工程支护设计中不能忽视围岩中间主应力的影响.

图5 围岩-衬砌特征曲线
3.3 不同参数影响下围岩变形结果对比
由图6可知,洞壁位移u0与锚杆轴力F随中间主应力系数b增加而减小,但围岩稳定系数k增大.因此,为了合理评价硐室围岩稳定以及节约支护成本,应选取合理反映围岩强度的b值.岩、土体剪胀效应对洞壁位移和锚杆轴力影响较大,但对围岩稳定系数无影响.此外,b越大,Ψ对u0与F影响越小,这表明采用Mohr-Coulomb强度准则高估了岩、土体的剪胀特性,不利于反应真实的围岩变形规律.考虑渗流场影响时(η=1),洞壁位移与锚杆轴力均增大.

图6 不同参数影响下围岩变形
3.4 围岩应力分布规律分析
由图7(a)可知,随着b增大,σr增大,σθ在塑性区增大在弹性区减小,且σθ最大主应力峰值增大,其峰值点左移.从图7(b)可知,剪胀角对围岩应力分布无影响.从图7(c)可见,考虑渗流影响时,围岩应力变化显著;随着pm增大,在围岩塑性区,σθ不变,但σr略有减小,在围岩弹性区,围岩应力均增大.此外,随着pm增大,最大主应力峰值增大且峰值点右移.

图7 不同参数影响下围岩径向(切向)应力分布
4 结 论
1)建立了渗流条件下锚杆支护圆形硐室力学模型,考虑剪胀、中间主应力以及渗流的影响,揭示了渗流场下锚杆加固硐室围岩受力与变形的演变规律.此外,理论解与数值解较小的差异验证了本文理论模型的合理性.
2)随着b增大,围岩塑性区应力明显增大,最大主应力峰值增大且峰值点左移,弹塑性界面半径、径向位移和锚杆轴力均减小,围岩自承载能力增加.因此,在工程中应根据实际工况和岩石力学特性试验,合理确定中间主应力系数的取值.
3)随着Ψ增大,虽对围岩塑性区半径和应力分布无影响,但洞壁位移和锚杆轴力急剧增大.然而,当b较大时,Ψ对围岩位移和锚杆轴力影响程度减小.因此,应根据围岩峰后强度与变形规律,适当考虑中间主应力效应,合理确定围岩剪胀角,避免支护设计不足和低估硐室实际变形.
4)考虑渗流场时,围岩塑性区半径、围岩径向位移和锚杆轴力明显增大,随着pm增大,围岩最大主应力峰值增大,围岩塑性区切向应力几乎不变,但径向应力减小,弹性区应力均明显增大,且应力分布不再以初始地应力为渐近线.

