基于LCL滤波的三相电压型PWM 整流器协同控制
高维士 严运兵 马 强 王晓东 朱博文
(1.武汉科技大学 汽车与交通工程学院, 武汉 430065;2.湖北文理学院 纯电动汽车动力系统设计与测试湖北省重点实验室, 湖北 襄阳 441053)
协同控制理论(synergetic control theory,SCT)所构建的被控系统状态空间流形,充分利用了理论的非线性特性和定向自组织原理,通过合适的流形使系统降阶,效果与滑模控制类似但不会出现抖振问题,保证了系统的稳态和动态性质[11].流形作为系统状态空间的约束变量,等价于吸引子的作用,其形成反映了直接自组织过程.相对于传统的控制理论而言,协同控制的闭环系统目标是变化的,无需对系统进行线性化处理,直接利用系统的非线性特性创建新的反馈方法[12].文献[13]提出了运用分布式SCT 的多拦截弹控制算法,通过改善其收敛速度及平滑性,实现了较强的鲁棒性,提高了控制系统的控制效率.基于SCT 设计的控制器结构更加简单、控制参数少、易于实现,适用于非线性系统控制,对研究解决现代复杂的综合性系统控制问题具有重要意义.
协同控制策略作为一种优秀的控制策略[14],已得到广泛关注,但其作为有源阻尼控制策略在LCLVSR 中却鲜有出现.本文以LCL-VSR 为载体,以去除谐振及降低THD 为目标,引入协同控制策略,提高系统运行精度及稳定性.
1 LCL-VSR 的开关函数模型
LCL-VSR 模型如图1 所示.ega,egb,egc是幅值为Um的交流电网电动势;0为中性点;Lg为电网侧等效电感;uca,ucb,ucc为电容电压;L为整流器侧等效电感;电网侧等效电阻Rg为电感Lg、滤波电容Cf和电压源的等效电阻之和;整流器侧等效电阻R为电感L和开关器件的等效电阻之和;整流器输入端电压及电流分别为v k和i k,k=a,b,c;igk为电网侧输入电流;输出电压为udc;电阻RL为等效负载;直流电容为C.
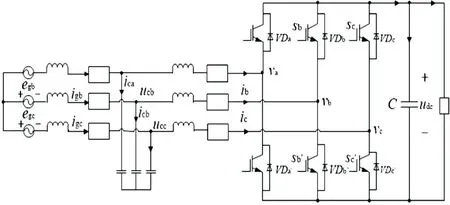
图1 LCL-VSR 主电路
为建立模型需要,现做以下假设:①电源为对称电源、滤波电感物理特性相同;②开关管为理想状态.sa、sb、sc为整流器开关函数.
根据KVL和KCL,可得LCL-VSR 的自然坐标系下的数学模型[15],见式(1):


2 VSR 的协同控制策略
2.1 协同控制器设计方法
协同控制器设计的基本思路就是确定描述系统状态变量关系的流形,并结合被控系统的状态方程综合求解系统的控制规律.
针对LCL滤波的整流器系统式(2),应用协同控制理论,求解二阶系统的输出量s d、s q,其系统状态方程为:
思雨想过去敲门,安慰解释一番,但他知道老婆的脾气。老婆是一个事业单位里的干事,工作清闲。但老婆是一个好强上进的女人,最开始为工作上的事闹心。后来思雨下海创业后,老婆便不再把心思全部用到单位里去了,而是把大部分时间都用到了家里。家里的事,思雨越来越顾不上,家中的一切琐碎杂事就都由老婆一人费力操办了。说句良心话,这些年,老婆为这个家付出得太多了。

式中:T1、T2为控制参数且均大于零,代表流形的收敛速度.在开关函数s d、s q的作用下,协同控制器通过控制参数T1、T2,使系统沿流形达到稳定平衡点.
2.2 协同控制收敛性分析
对LCL-VSR 控制系统进行误差分析,求解误差.联立式(7)和(8)得:

式中:K1、K2、K3、K4为常数,显然K1、K2、K3、K4的取值,均不影响误差ξ收敛至零点.
2.3 控制器的设计

联立式(4)、(13)~(15)、(17)可得开关函数
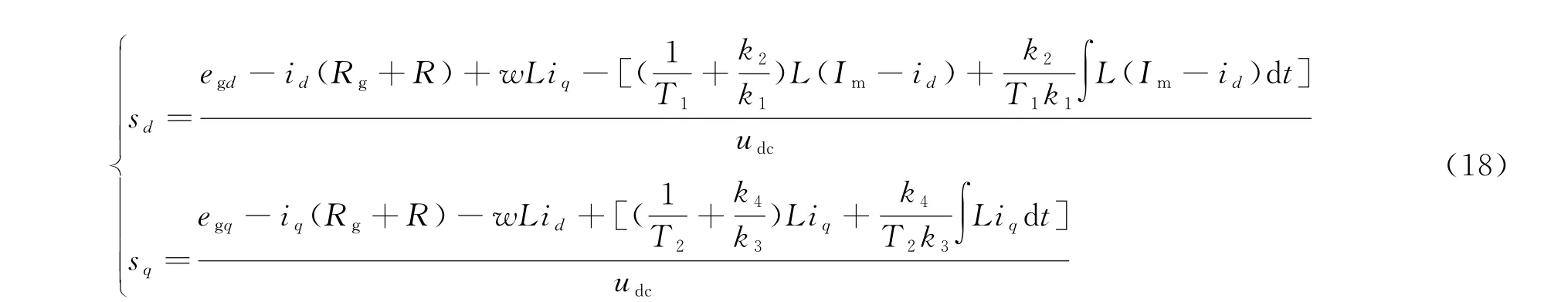
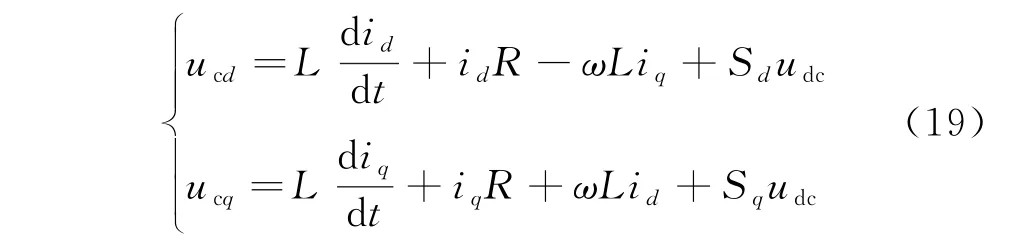
将式(18)所得的s d、s q代入式(19)得到uc的dq分量,此后经过空间矢量脉宽调制即可生成开关脉冲驱动信号,实现电压调制.
基于上述求解过程,图2给出协同控制方法的流程图.
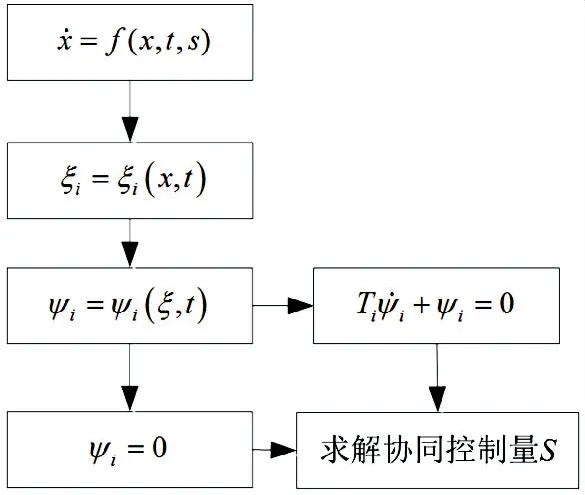
图2 协同控制方法流程
3 仿真实验分析
3.1 仿真设计
由式(16)、(18)、(19),利用Matlab-Simulink软件搭建基于LCL滤波的三相电压型PWM 整流器协同控制仿真模型,LCL-VSR 协同控制系统如图3所示.

图3 LCL-VSR 协同控制系统
仿真实验的的主要参数见表1.

表1 仿真实验的主要参数
3.2 仿真实验结果及分析
3.2.1 额定负载RL=50Ω 时的谐波及功率因数分析
额定负载RL=50Ω 时的a相网侧电流谐波如图4所示.其中作为对比的电压前馈解耦控制L滤波的VSR,除不含有滤波电容Cf,总电感与LCL-VSR 总电感相等外,其他参数未做任何修改.
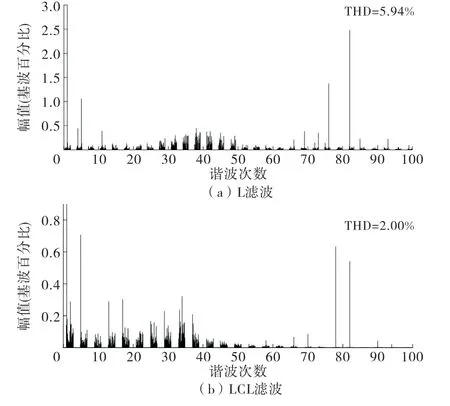
图4 额定负载时的a相电网侧谐波分析
本文采用比例-积分的流形形式,式(6)中的x*i-x i,意味着引入了i d、i q等误差反馈,则式(7)为引入比例-积分形式的误差反馈,通过开关函数式(18)中的控制参数k i、T i调整,不仅使谐波含量有所降低,有效消除了谐振现象,同时稳定性也有所改善,如THD 会随着k3增大而降低,但输出电压会有超调等.
由图4可知,LCL-VSR 较电压前馈解耦控制L滤波器各次幅值及THD 都有较大降低,THD 由5.94%下降到2.00%.从图4(b)可以观察开关频率处的高次谐波(80次)能够产生较好的滤除效果,很好地实现了采用LCL 滤波器的目的.同时对10~40次谐波段分析并无谐振频率出现,特别是在1.77 k Hz(35次谐波)处无谐振点[16],这说明LCL-VSR 的协同控制策略对谐振有良好的抑制作用.
通过图5分析可知,网侧电压与电流能够很好地保持同相位稳定运行,功率因数为0.997,实现了高功率运行的目的.
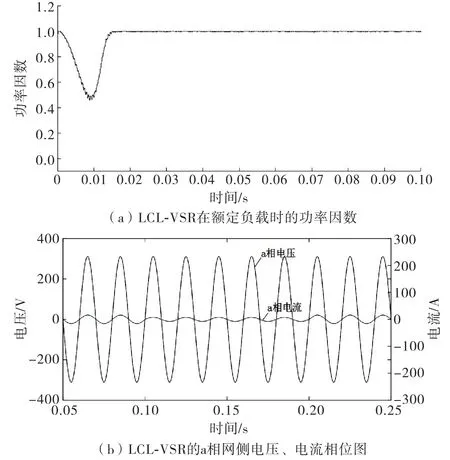
图5 额定负载时的功率因数和网侧电压、电流相位关系
由以上的谐波含量及功率因数分析,均可得出LCL-VSR 的协同控制策略具有较好的谐波抑制能力,能够有效去除谐振现象,实现整流器高功率稳定运行.
3.2.2 额定负载、过载及轻载情况下的稳态性能分析
为了有效验证协同控制策略的控制精度及稳定性,以下将进行额定负载、过载RL=25Ω 及轻载RL=100Ω 情况下的稳态性能分析.
图6为额定负载RL=50Ω 情况下的仿真结果.图7为过载RL=25Ω 情况下的仿真结果.图8为轻载RL=100Ω 情况下的仿真结果.

图6 R L=50Ω 仿真结果

图7 R L=25Ω 仿真结果

图8 R L=100Ω 仿真结果
由仿真图观察可得,基于协同控制策略的LCL-VSR 控制系统在额载、过载及轻载3种情况下的udc(iL)进入稳态时间分别为15.2 ms、15.6 ms和15.2 ms,其他数据见表2.
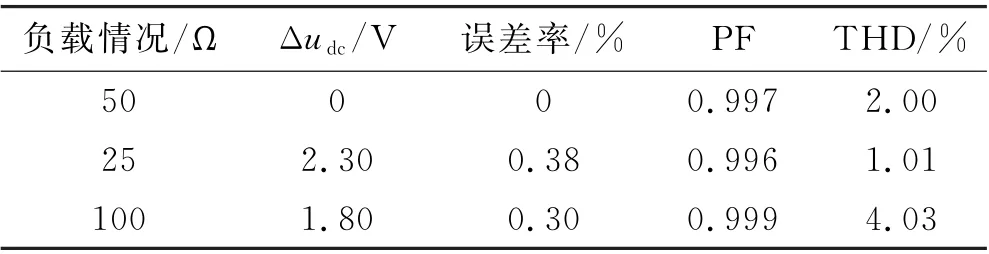
表2 仿真稳态结果
3.2.3 负载突变情况下的暂态性能分析
过载突变情况仿真结果如图9所示,额定负载在0.1 s突变为过载状态.图9(a)电压最大误差为5.0 V,误差比例为0.83%,图9(b)电流最大误差为0.20 A,误差比例为0.83%,且均在16 ms后进入稳定状态.

图9 过载突变仿真结果
轻载突变情况仿真结果如图10所示,额定负载在0.1s突变为轻载状态.图10(a)电压最大误差为2.7 V,相对误差比例为0.45%,图10(b)电流最大误差为0.03 A,误差比例为0.5%,在1 ms后进入稳定状态.
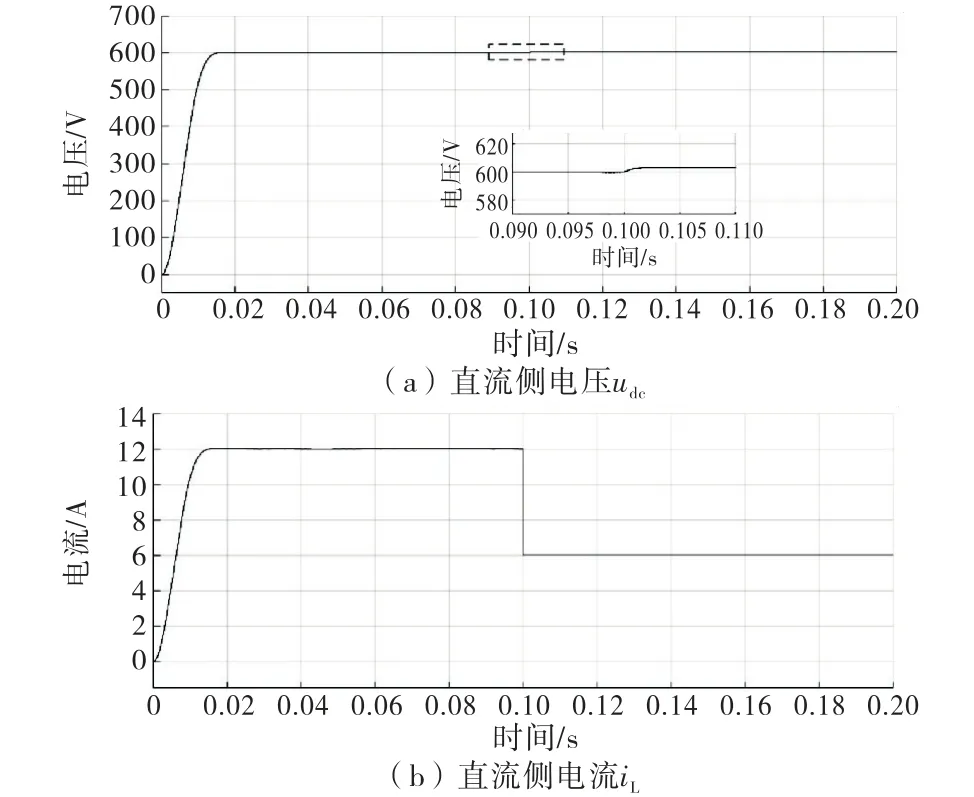
图10 轻载突变仿真结果
通过稳态及暂态性能分析,可得出基于协同控制策略的LCL-VSR 控制器收敛速度及控制精度较好,控制策略可行.
4 结 语
针对传统PWM 整流器的谐波含量高、控制精度低、抗扰性能差等不足,本文提出运用以协同控制理论为基础的LCL-VSR 有源阻尼控制策略设计控制器.同时为提高控制精度及稳定性采取了比例-积分的流形形式.与现有的研究方法相比,由于发挥了LCL 型滤波器及协同控制策略的优点,在有效降低入网电流波形总畸变率的基础上,利用协同控制策略有效抑制了谐振现象,为VSR 的精确运行和THD的降低提供了依据.通过仿真实验分析,其响应速度及抗扰性能都较好,实现了高功率因数运行和THD的有效降低.

