隧道机械化全断面施工条件下爆破振动传播规律测试与分析
张新尚, 张中哲, 郭鸿雁
(1.云南建设基础设施投资股份有限公司, 昆明 650501; 2.招商局重庆交通科研设计院有限公司, 重庆 400067;3.重庆交通大学, 重庆 400074)
钻爆法因成本低、适用性强等优点被广泛应用于隧道施工中,但爆破法施工不可避免要产生爆破地震效应,当地表振动效应较大时,会对周边环境造成巨大影响。因此,分析、预测隧道爆破开挖作用下的地表振动特征是隧道进行安全爆破施工的前提,已有研究对人工爆破法施工条件下的爆破振动传播规律研究较多。目前,国内隧道建设规模庞大、隧道现场施工人力资源日益紧张且人工成本逐年增长,传统的施工组织模式已不能适应隧道工程建设的需要,机械化爆破法施工已成为隧道施工发展的趋势[1],但目前对机械化施工条件下的爆破振动传播规律研究较少。因此,为保证隧道建设工程安全、高质量、高效率的完成,亟需开展相关研究,为隧道机械化爆破法施工提供指导。
目前,爆破振动的分析主要采用现场监测和数值模拟2种手段。从20世纪50年代开始,我国各研究单位和高等院校结合有关爆破的科技计划项目,对爆破地震波的传播规律和作用机理进行了理论分析、试验、统计归纳[2-7],在参照国外相关标准及国内研究现状下制定了国内建筑物爆破破坏标准。李胜林等[8]结合地表振动测试数据以及理论回归分析结果,预测了浅埋地表隧道爆破振动速度传播规律。Singh[9]建立有限元模型对不同岩石材料、装药量、炸药起爆顺序等不同影响因素下进行了爆破振动速度的预测。姚勇等[10]结合紫坪铺隧道小净距段现场实测爆破振动数据,通过二维和三维数值模拟计算,分析了小净距隧道爆破施工中后行隧道爆破对先行隧道的影响因素,得出先行隧道迎爆侧及开挖掌子面前后1倍洞径范围是影响较大部位。
总结分析目前隧道爆破振动规律现状及相关研究成果,有以下几点认识:1) 研究多基于人工钻爆法施工的浅埋隧道,对机械化钻爆法施工隧道的爆破振动规律研究报道较少;2) 机械化全断面爆破法施工与传统分步爆破相比,爆破规模大,对围岩稳定性影响大,需深入研究机械化全断面施工条件下的爆破振动规律研究;3) 爆破振动的研究多数是对临近建构筑物的影响而展开,对爆破振动特点在空间上的分布情况研究较少。为此,本文在已有研究现状分析的基础上,结合依托工程,通过三维数值仿真模拟,分析爆破振动特征及空间分布规律,并开展现场测试进行验证对比,以便为机械化大断面施工条件下隧道爆破振动的预测与安全控制提供依据。
1 理论研究
质点振动位移峰值、速度峰值或加速度峰值等是衡量爆破震动强度的重要指标,但以哪种物理量作为衡量标准最合适,国内外有不同的观点。在爆破工程中,爆破地震作用作为一种动力作用,为区别于静力作用,广泛采用速度峰值和加速度峰值作为衡量指标。后来人们通过大量观测,结果表明爆破地震破坏程度与振动速度的大小的相关性较好;且当炸药量、爆心距和最小抵抗线相同,而传播地震波的岩土介质有变化时,较加速度而言,振动速度与岩土性质有更稳定的相关关系,规律性更好。因此,目前多采用速度来表征爆破震动强度。
由于影响爆破震动强度的因素诸多,难以找出表述爆破震动强度的具体数学函数表达式。世界各国学者从试验入手,运用量纲分析,得出了较多的经验公式。中国目前多采用萨道夫斯基经验公式进行参数优化、爆破设计及振速预测[11]。萨氏公式只要在前期确定好K、α值,在施工过程中,通过测出爆破区域与监测点之间的距离便可较准确地控制爆破最大振速,最大限度地减少对周边环境的影响,具有较强的实用性和参考性,因此本研究采用如下萨氏公式:
(1)
式中:Q为装药量(齐发爆破时为总药量,延期爆破时为单段最大装药量),kg;R为测点至爆源的距离,m;K、α是与爆破条件、介质等有关的系数。
2 工程概况
蔓耗至金平高速公路起始于个旧市蔓耗镇西北侧附近,连接在建的元江至蔓耗高速公路,终点止于金平县城附近,连接规划的金平至金水河高速公路,主线全长50.58 km,全线共设隧道16座,其中草果山隧道为本项目建设的控制性工程。隧道起讫桩号:左线ZK33+947.04~ZK40+952,右线YK33+955~YK40+960,长7 005 m,为特长公路隧道,最大埋深902.5 m。隧道区海拔高程介于1 125.1 m~2 126.0 m之间,相对高差1 001.0 m,属构造剥蚀高中山地貌区。隧道地质条件复杂。
3 三维数值仿真分析
3.1 模型建立
采用大型有限差分软件FLAC3D进行模拟,考虑到边界效应,为简化模型,建立模型尺寸为100 m×100 m×100 m的模拟区域。为了减少模型边界上波反射的影响,通过阻尼器与自由场网格进行耦合建立自由场边界,包括4个平面网格和4个柱体网格。其中,阻尼器采用瑞利阻尼;平面自由场网格是二维计算,假设在面的法向无限延伸;柱体自由场网格是一维计算,假设在柱体两端无限延伸。模型如图1所示。为更好地进行研究,对隧道周围及掌子面处进行分块及网格加密处理,并结合FLAC3D内置编程语句,考虑所有爆破孔位的荷载作用,除静力计算假定外,孔位作用考虑主要通过如下几步实现:
1) 根据爆破孔位的性质不同,通过计算机辅助设计软件提取所有孔位的坐标信息与爆破设计信息。
2) 通过FLAC3D内置fish语句自动查找指定里程隧道开挖周围荷载作用面。
3) 对于某一台阶开挖,通过FLAC3D内置fish语句计算单个爆破孔位爆破后,作用于周围单个受载面的动力作用。
4) 通过FLAC3D内置fish语句,罗列此开挖台阶所有孔位在此受载面的动力作用,并求取合力。
5) 通过FLAC3D内置fish语句罗列此开挖台阶所有孔位在所有受载面的动力作用。
6) 通过FLAC3D内置动力计算模块实现爆破动力作用。
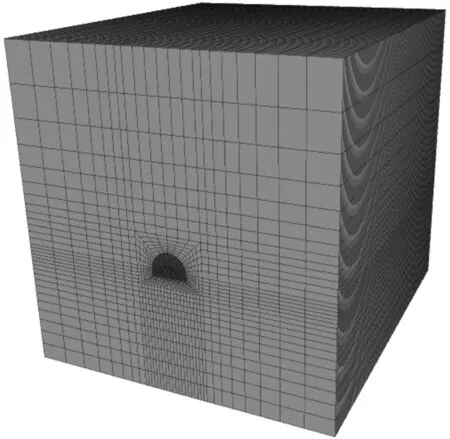
3.2 计算参数及工况
考虑依托工程地质条件,围岩主要为Ⅳ级围岩,拟定分析工况如表1所示。采用公式(2)[12]计算围岩和混凝土衬砌的弹性模量和泊松比,并查阅常见岩石完整岩块动力变形参数表,计算结果如表2所示。
(2)
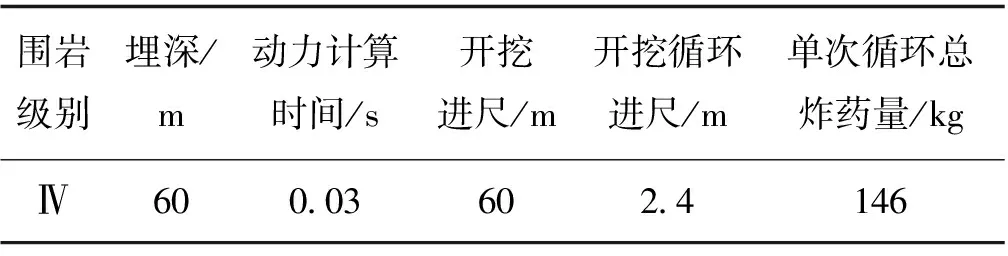
表1 计算参数及工况

表2 围岩及仰拱弹性模量和泊松比计算参数
3.3 计算结果分析
1) 纵向传播规律
不同监测部位与掌子面的距离不同,导致在不同位置上监测点记录的峰值振速不同。为研究不同测点距爆源不同距离的振速分布规律,本次模拟设置4个研究断面,分别距离掌子面20 m、40 m、60 m、80 m。通过对每个断面的拱顶、拱腰、边墙、墙角和仰拱进行爆破振动速度分析,研究隧道爆破振动响应的纵向分布规律。爆破振动速度变化规律如图2~图6所示。通过萨道夫斯基经验公式对爆破振动速度进行拟合,得到爆破峰值速度空间分布规律,如图7所示。
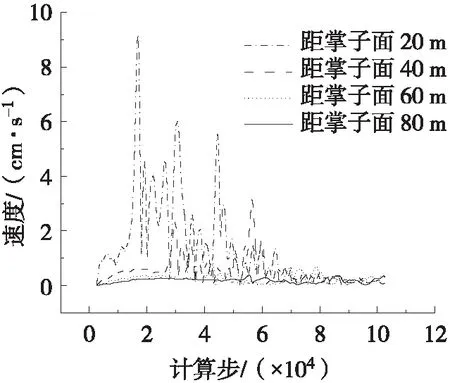
图2 拱顶爆破振动速度变化规律
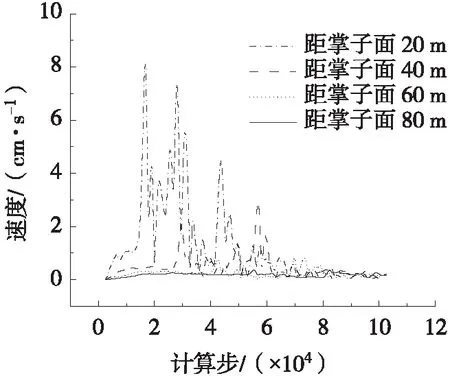
图3 拱腰爆破振动速度变化规律
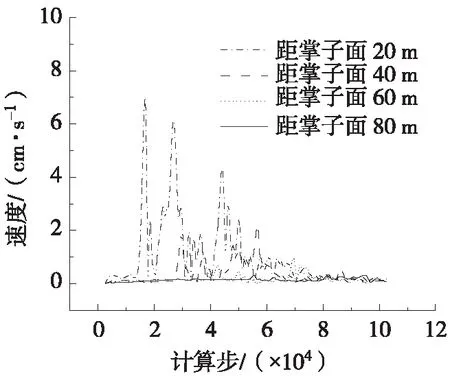
图4 边墙爆破振动速度变化规律
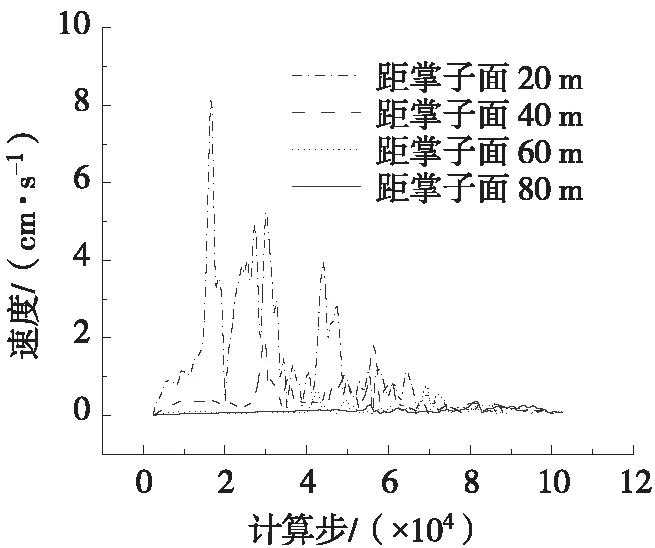
图5 墙脚爆破振动速度变化规律
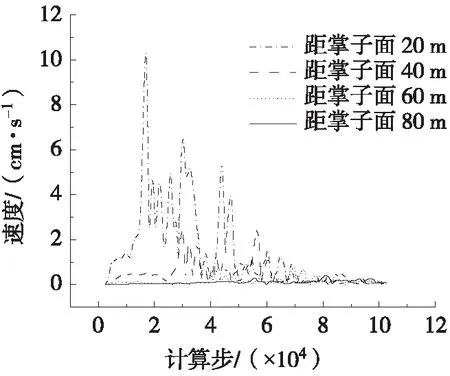
图6 仰拱爆破振动速度变化规律
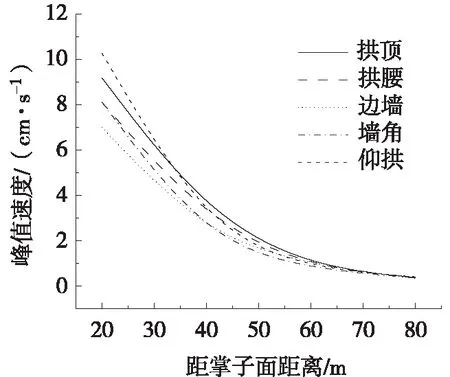
图7 爆破峰值速度空间分布规律
由图2~图6可知:1) 随着与掌子面距离的增加,不同监测断面上同一监测部位在爆破荷载作用下的振动速度的绝对值明显减小,振动速度峰值的出现时间也随距离的增加而推迟;2) 同一监测断面上不同监测部位的振动速度值随时间的变化规律较为一致。由图7可知,爆破振动峰值速度随距掌子面距离的增加而减小;爆破振动峰值振速在空间上的分布符合萨道夫斯基经验公式,由此可得到不同监测部位场地系数K与衰减系数α,如表3所示。

表3 场地系数K和衰减系数α取值汇总
2) 径向传播规律
在同一研究断面,不同监测位置的爆破振动速度沿隧道径向深度的增加也有不同变化。为研究相同断面下不同测点在径向深度不同时的振速分布规律,本次仿真模拟以距开挖掌子面40 m的断面为研究断面,分别在拱顶、拱腰、边墙、墙角以及仰拱等位置布置振动速度监测测线,分析围岩深部振动特性传播规律。测线长度均为8 m,每条测线上布置9个监测点,间距为1 m,如图8所示。围岩峰值速度衰减曲线如图9所示。
由图9可知:1) 爆破振动峰值速度与开挖轮廓线距离呈线性递减关系,在距开挖轮廓线0 m~4 m时,峰值速度变化明显;距开挖轮廓线4 m~8 m时,曲线斜率降低,峰值速度变化较小;2) 不同测线爆破振动峰值速度的衰减趋势大致相同;3) 不同测线围岩峰值速度大都在距开挖轮廓线6 m~8 m时开始收敛,因此,可得出隧道爆破荷载对Ⅳ级围岩径向的影响范围为6 m。
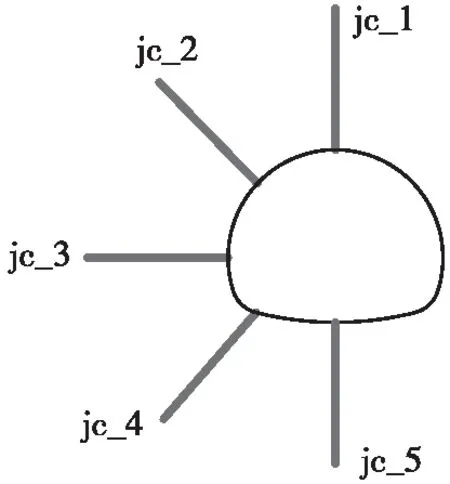
图8 围岩速度测线示意

图9 围岩峰值速度衰减曲线
4 现场测试与分析
4.1 测试方案
1) 测试段落选取
方案以爆破振动速度为主要测试指标,测试段落选取隧道机械化施工试验段,实际测试的段落为草果山隧道进口右洞YK35+750~YK36+150,累计测试段落长度为400 m。该段地质条件较为复杂,具有一定的代表性,围岩以基性岩和二长岩为主,多呈强-中风化,块状构造,节理裂隙较发育,岩体较破碎,多呈碎块状碎裂结构;物探结果表明,多为低阻区;岩体富水性较强,开挖时可能存在较大量的滴水、渗水等现象。
2) 振动测点布置
为获取爆破振动速度纵向分布规律,并考虑到现场测试的便利性与安全性,在隧道掌子面附近边墙位置预留洞室设置爆破振动测点,并安装TC-4850爆破测振仪进行爆破振动测试,现场跟随施工进度,采集每一个爆破作业循环的爆破振动规律,直至二衬施工完为止。测点布置示意如图10所示。
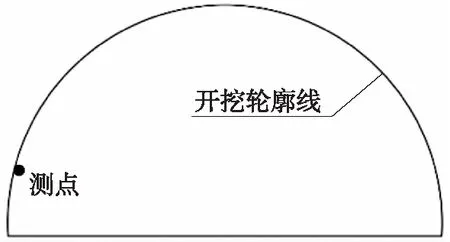
(a) 横断面测点

(b) 纵断面测点

(c) 现场测点处预留洞室
4.2 测试结果分析
测试设置爆破震动测试测点2个,跟随施工进度循环,测试爆破震动61次,提取隧道施工过程中不同爆破能量作用下,距掌子面不同距离的拱顶爆破振动参数(爆破振动速度与振动频率等),分析爆破振动参数在时间与空间上的发展变化规律。爆破振动速度随掌子面的距离增大的变化规律如图11所示,爆破振动半坡主频随掌子面的距离增大的变化规律如图12所示。
通过现场实测的方式对隧道中爆破振动规律进行测试与分析,结果表明:隧道施工过程中爆破振动速度与半波主频随距掌子面距离的增大而逐渐减小,爆破振动对围岩的影响也逐渐较小。根据爆破安全规程,如果按2 cm/s进行安全控制,爆破振动的影响范围约为67 m。
为了验证数值仿真结果的准确性,将实测结果与式(1)计算结果进行对比。其中,边墙的场地系数K、衰减系数α见表3,V基于爆破安全规程取为2 cm/s,Q为146 kg,计算得到测点至爆源距离R为62.95 m,与现场实测结果相近。

图11 爆破振动速度随掌子面距离变化规律
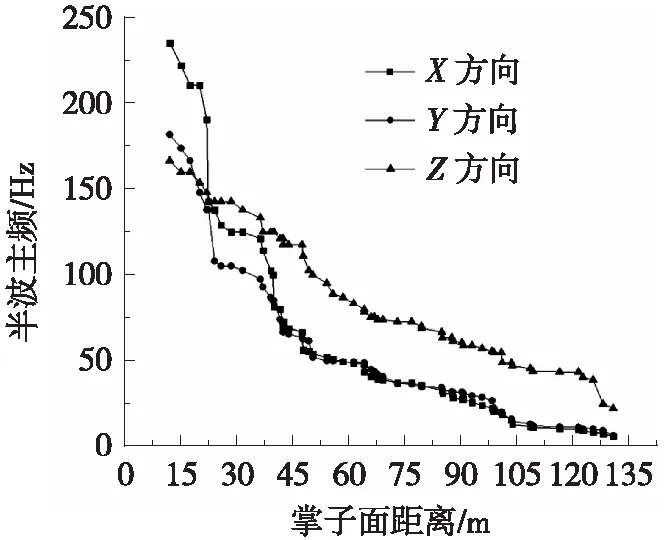
图12 爆破振动半坡主频随掌子面距离变化规律
5 结论
机械化钻爆法施工是隧道施工发展的趋势。本文依托草果山隧道进行研究分析,得到了机械化大断面施工条件下爆破振动特征及传播规律,为机械化大断面施工隧道爆破振动的预测与安全控制提供依据,为指导机械化钻爆法施工提供理论基础。
1) 沿隧道纵向方向,通过研究不同测点在距开挖面不同距离条件下的爆破振动速度分布规律,采用萨道夫斯基经验公式对结果进行拟合,得到不同测点的场地系数K和衰减系数α值。基于爆破安全规程,按2 cm/s峰值速度进行安全控制,以边墙为例,当场地系数K为252.49、衰减系数α为1.95时,计算得到测点到开挖面距离R为62.95 m,与现场实测结果67 m相近,故相似工程可参考本文得出的场地系数和衰减系数。
2) 沿隧道径向方向,随着距隧道开挖轮廓线深度的不断增加,不同测线都呈现衰减的规律,且不同测线上围岩峰值速度衰减规律基本一致。由于隧道开挖导致其轮廓线周围一定范围内的岩体出现松散等情况,模拟结果显示,当距离大于6 m时围岩峰值速度开始收敛,故建议取爆破振动对围岩径向影响范围为0 m~6 m。
3) 结合三维仿真分析及现场试验段实测等手段,得到了依托工程Ⅳ级围岩条件下爆破振动速度在空间上的分布规律,但对其他地质条件下的隧道可能不具有普遍的适用性,需结合实际情况进一步研究。

