ν-t图巧解带电粒子在电场中的运动问题

>>>廉新萍

《普通高中物理课程标准（2017年版）》指出：“运用物理知识解决实际问题能力的高低，往往取决于学生将情境与知识相联系的水平。”我们常说某个问题很“活”，其实“活”的本质之一在于情境的转化，能不能把问题中的实际情境转化成物理情境，是应用物理观念思考问题、应用物理知识分析问题，进而建立相应物理模型的关键，而ν-t图不失为打开情境转化之门的一把金钥匙。

一、ν-t图能把运动现

带电粒子在电场中的直线运动不外乎加速、减速、匀速这三种形式，弄清运动过程是解决此类问题的关键，利用ν-t图恰恰可以展示带电粒子在某时刻的速度、某段时间段内的位移。

例1．如图1所示，在P板附近有一电子由静止开始向Q板移动，已知两极板间的电势差为U，极板间距为d，电子质量为m，电量为-e。分析：当将两极板间的电势差增加一倍（其他条件不变）和将极板间距d增大一倍（其他条件不变）时，求电子到达Q板的时间和速度变化情况。

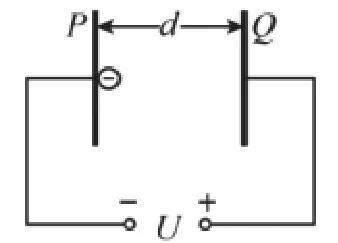
图1

【思路】电子在电场中做匀加速直线运动，作出ν-t图如图2所示，到达Q板时间为t1，速度为ν1。若将两极板间的电势差增加一倍（其他条件不变），则电场强度加倍，加速度加倍。由于位移不变，即图线与时间轴围成的面积不变，可知电子到达Q板的时间t2＜t1，速度ν2＞ν1。

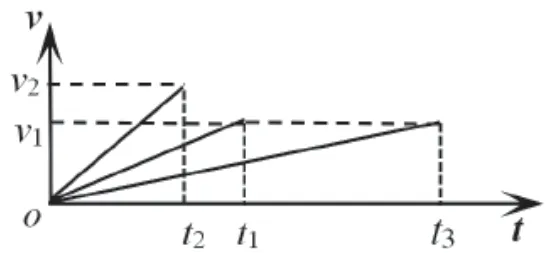
图2

若将极板间距d增大一倍，则加速度减半，由于位移加倍，即图线与时间轴围成的面积是原面积的2倍，即×t3，可得电子到达Q板的时间t3＝2t1，而电子到达Q板的速度保持不变，仍为ν1。

【方法提炼】

电场中粒子匀加减，运动要用ν-t展；

斜率来把加速度现，位移就用面积看。

二、复杂运动更直观

当带电粒子所处电场为交变电场时，粒子运动加速度会发生变化，时而加速时而减速，时而正向运动，时而反向运动，但利用ν-t图可以使复杂运动清晰与直观。

例2．如图3所示，两平行正对的金属板A、B间加有如图4所示的交变电压，一重力可忽略不计的带正电粒子被固定在两板的正中间P处。（设A、B间距离足够大）。

图3

图4

现分析在t=0时刻释放该粒子，粒子最终打在哪个板上。

板间为匀强电场且场强方向向右，由于粒子带正电，所以受到的电场力向右，从t=0开始，粒子向右做匀加速直线运动，当t=T—2时，速度达到最大为ν1。在内电场反向，加速度反向，粒子向右做匀减速直线运动。由于两段时间内加速度大小相等，因此当t=T时，速度刚好减为零。之后重复0-T内的运动形式，这一运动的ν-t图如图5所示。图线与时间轴围成的面积始终处于横轴上方，表示粒子一直向右运动，所以在t=0时刻释放该粒子最终会打在B板上。

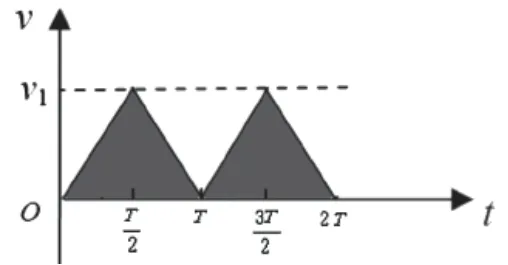
图5

若在t0时刻释放该粒子，粒子会时而向A板运动，时而向B板运动，并最终打在A板上。求t0可能属于的时间段（设0＜t0＜T）。

【分析】先找从特殊时刻（如）释放的粒子，由于内UAB＞0且保持不变，可知，粒子受到的电场力向右，该段时间内向右做匀加速直线运动，t=T—2时最大速度为ν2，作出ν-t图如图6所示。在内电场反向，加速度反向，粒子先向右减速到零，再向左加速，在t=T时，速度变为-ν2；接下来，电场反向，粒子向左做匀减速直线运动时，速度变为0。之后重复内的运动形式。图线与时间轴围成的面积如果在时间轴上方，代表粒子位移为正，即该段时间内，粒子向右运动；图线与时间轴围成的面积如果在时间轴下方，代表粒子位移为负，即该段时间内，粒子向左运动。由ν-t图可以发现，粒子从P点出发，先向右方（正方向）运动一段位移（横轴上方对应的三角形面积），再向左方（负方向）返回运动一段位移（横轴下方对应的三角形面积），到达P点，然后又向右重复上述运动，即粒子在P点右侧做往返运动，但不会打到A板上。

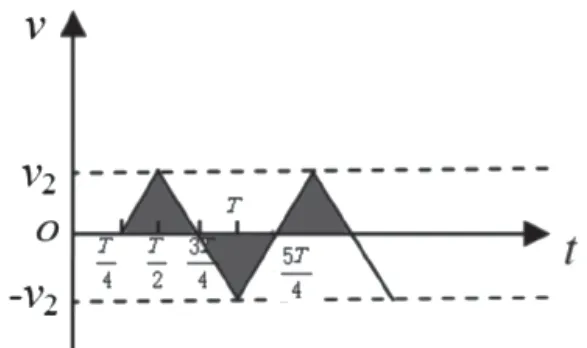
图6

图6 也可以认为是将图5的两个坐标轴进行平移而成，即纵轴向右平移到，此时纵轴与图线的交点就是横轴应向上平移到的位置，如图7所示，可看到新图象与图6效果相同。

图7

与计算法相比，坐标轴平移的方法较为简单。以下分析均采用坐标轴平移的方法。

要想使粒子时而向A板运动，时而向B板运动，并最终打在A板上，需要使t'轴上方图线与t'轴围成的面积小于t'轴下方图线与t'轴围成的面积。可得使粒子在内释放（平移坐标轴后的ν'-t'图如图8所示）；或粒子内释放（平移坐标轴后的ν'-t'图如图9所示），粒子最终会打在A板上。

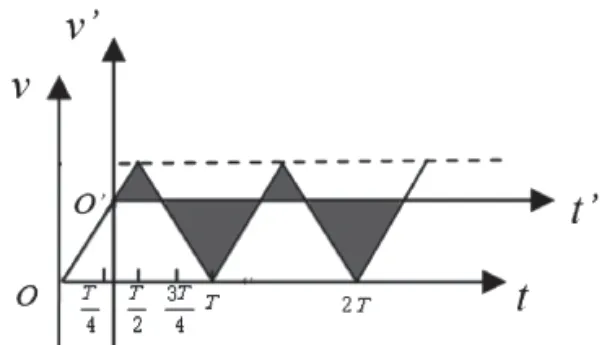
图8

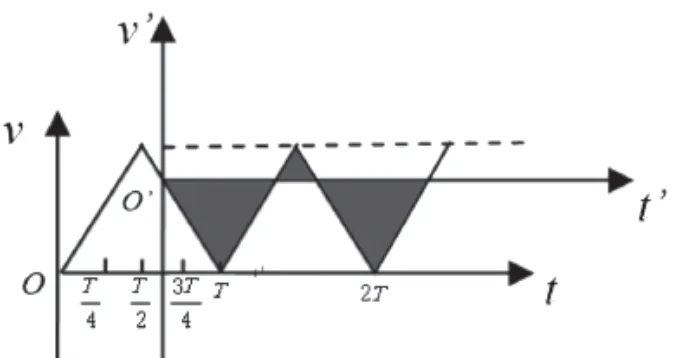
图9

【方法提炼】

初态分析是基础，坐标平移到要求处；

上下面积有“方向”，合面积为负反向了。

三、最大位移面积找

除了可以用ν-t图找运动形式外，还可以从ν-t图找粒子运动的最大与最小位移。

例3．如图10所示，水平正对放置的金属板A和B的距离为d，它们的右端放着垂直于金属板的靶MN，现在A、B板上加上如图11所示的电压，电压的正向值为U0（A板电势高于B板电势），反向值为且每隔变向1次。现将质量为m、带电荷量为+q的粒子束从A、B左侧的中点O以平行于金属板的方向射入两板之间，设粒子能全部打在靶上且所有粒子在A、B间的飞行时间均为T。不考虑重力的影响。求在距靶MN中心O'点多远的范围内有粒子击中。

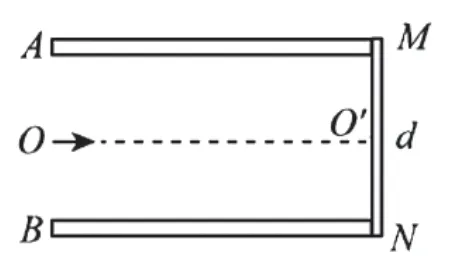
图10

图11

【分析】粒子打在靶MN上的范围，实际上就是粒子在竖直方向所能到达的范围。带电粒子在电场中做类平抛运动，水平、竖直方向的分运动等时且独立，因此，粒子在竖直方向的分运动用时也为T。根据可知，内的加速度为内加速度的2倍。在t=0时刻射入电场的粒子，受到的电场力向下，所以粒子在竖直方向向下做匀加速直线运动，时竖直方向的速度为ν。在内电场反向，加速度反向且大小减半，粒子在竖直方向向下做匀减速直线运动，在t=T时，竖直方向的速度变为此时粒子离开电场。作出竖直方向运动的ν-t图如图12所示，图线与时间轴围成的面积表示粒子向下运动的位移。

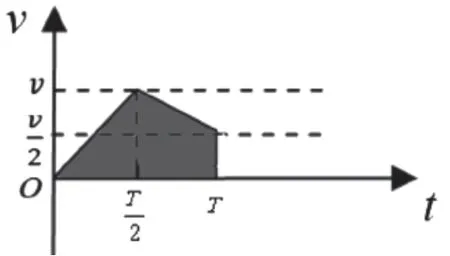
图12

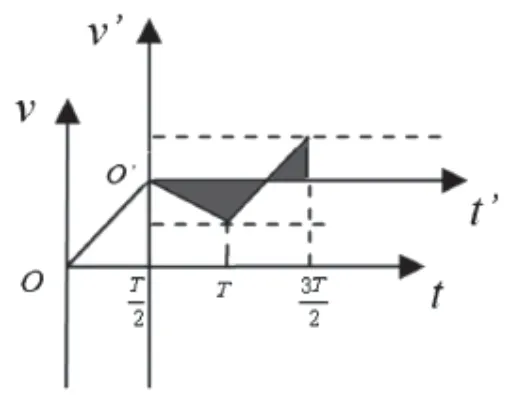
图13

【方法提炼】

曲线运动分解现，选择分运动画ν-t；坐标平移省计算，找坐标原点很关键。