2021年新高考全国卷Ⅰ数学18题评析

>>>伊翠红

2021年新高考全国卷Ⅰ数学18题以“一带一路”知识竞赛为背景，考查考生对概率统计基本知识的理解与应用。试题就选手答题得分而设问，既考查相关数学知识，又考查关键能力；既突出数学知识的基础性，又突出数学模型的应用性。本文旨在分析考生在试题解答过程中出现的一些问题，并对2022年高考概率统计的复习提出些许建议。

一、试题再现

18.(12分)

某学校组织“一带一路”知识竞赛，有A，B两类问题．每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答，若回答错误则该同学比赛结束；若回答正确则从另一类问题中再随机抽取一个问题回答，无论回答正确与否，该同学比赛结束．A类问题中的每个问题回答正确得20分，否则得0分；B类问题中的每个问题回答正确得80分，否则得0分．

已知小明能正确回答A类问题的概率为0．8，能正确回答B类问题的概率为0．6，且能正确回答问题的概率与回答次序无关．

（1）若小明先回答A类问题，记X为小明的累计得分，求X的分布列；

（2）为使累计得分的期望最大，小明应选择先回答哪类问题？并说明理由．

解：（1）X的取值可能为0，20，100.

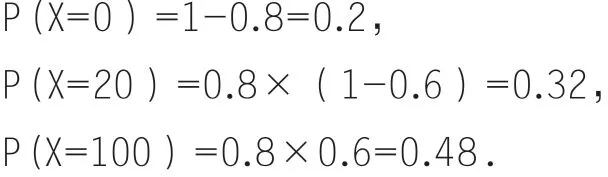
∴х的分布列为

?

（2）假设先答B类题，得分为Y，

则Y可能为0，80，100．

∴Y的分布列为

?

∴E（Y）=0×0.4+80×0.12+100×0.48=57.6．

由（1）可知E（X）=0×0.2+20×0.32+100×0.48=54.4．

∴E（Y）＞E（X），

应先答B类题．

二、错例典析

试题背景具有鲜明的时代特色，通过考生熟悉的答题竞赛活动进行设问，考查概率统计基础知识的应用。有些考生在解答时存在诸多不妥之处，下面举例说明。

1.文字阅读不认真，造成审题失误

从第（1）问即开始丢分，如图1—图4。

图1

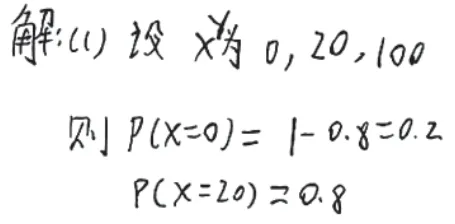
图4

试题文字材料近300字，每漏读一字，对题意的理解都可能出现偏差。图1与图2考生显然都没能正确写出随机变量X的三个取值；图3与图4考生虽然正确写出了随机变量X的三个取值，但分别对“X=0”和“X=20”的概率取值出现计算方面的错误。此类考生都没有认真阅读题目材料，没有从中提取出完整的答题有效信息，造成失分。

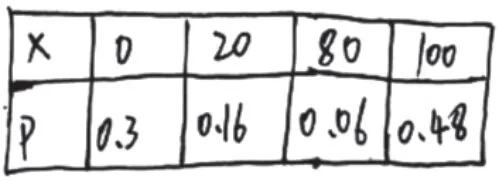
图2

图3

2.数学概念不清晰，公式选择不恰当

如图5—图7。

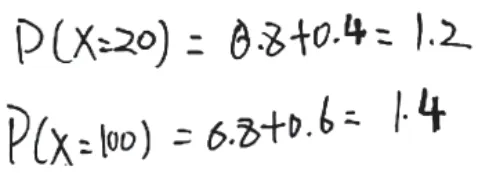
图5

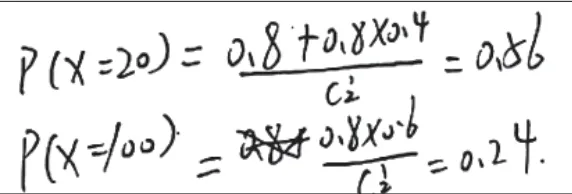
图7

对数学概念的理解要清晰，对数学公式的运用要精准。显然，三名考生在求解问题（1）时，对“X=20”和“X=100”的概率取值计算都没有选对公式。图5考生把问题理解为互斥事件的和事件，采用概率加法公式；图6考生把问题理解为独立重复试验，采用n次独立重复试验有k次发生的概率计算公式；图7考生则错把古典概型融入。他们共同失误是，对随机变量X的取值对应的事件及彼此关系没有进行正确分析，概念混淆、公式错乱，造成失分。

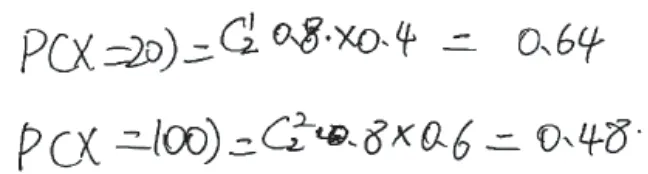
图6

3.运算过程出现失误，致使结果不准确

如图8和图9。

图8

图9

数学的关键在于运算，运算结果能为解决问题提供数据支撑。在求解问题（2）时，需要比较两类方案中小明答题得分的数学期望，以做出有利决策。虽然他们所列的表达式正确，但最终的计算结果却都是错误的。此类考生的共同问题在于平时没有养成认真作答、提高精准率的好习惯，致使考场答题失分。

4.数据分析、推理不严谨，出现跳步作答

如图10和图11。

图10

图11

推理与证明是数学特有的思维方式。在解决问题（2）时，图10考生直接得出两种方案下的随机变量数学期望值分别为54.4和57.6，但对这两个数据的由来却缺少必要的说明；图11考生直接得出数学期望的结果为57.6，而对于数据9.6与48的由来也没有提供数据支撑。此类考生的共同错误是对问题结论的得出缺少必要的数据说明，缺少数据分析、推理不严谨，属于跳步作答，造成失分。

5.对概率的意义、性质理解不到位

出现常识性错误，如图12和图13。

图12

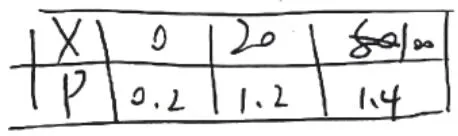
图13

概率是描述随机事件发生可能性大小的量，其取值范围为[0，1]。图12考生显然没有注意到分布列中随机变量X所有取值概率之和大于1这一点；图13考生更是出现了随机变量X单个取值概率大于1的错误解答。他们的共同失误是对概率的意义、分布列的性质理解不到位，致使出现常识性错误，造成失分。

6.公式书写不规范，数据表达不准确

如图14和图15。

图14

图15

数学语言具有简洁性、准确性的特点。图14考生在书写随机变量X的分布列时，对其概率取值直接列式表达，未给出最简结果，属于结果表达不简洁；图15考生书写随机变量数学期望公式时，未使用加权平均数х1p1+х2p2的表达式，属于书写不规范。此类考生的共同缺点是数学符号表达不规范，不符合数学语言简洁性和准确性的要求，造成失分。

7.书写混乱，字迹不清，影响视觉

如图16。

图16

字迹清晰是保障阅卷老师顺利阅卷的前提，也是确保考生取得相应分数的必要条件。图16考生答卷时字迹潦草不清晰，可能会影响阅卷老师对答题过程的准确评判，也可能会影响考生自己的成绩。此类考生的共同缺点是平时不注重书写训练，没有养成书写清晰、表达规范的好习惯。

三、备考建议

总结、反思以上作答中存在的问题，针对概率统计知识的复习备考，提出以下建议。

1.重视材料阅读训练，提高信息提取、加工、处理的能力

阅读中，要用数学的眼光观察问题，通过直观观察或抽象描述，完整提取相关信息，再运用所学数学知识解决实际问题。如该试题文字叙述极为精简，增之一字不必，减之一字不可，漏读一字对题意的理解都会出现偏差。如“有A，B两类问题”“能正确回答问题的概率与回答次序无关”等语句，对问题的分析、判断、求解都起着至关重要的作用。

2.重视教材，熟悉概率相关概念的产生背景，理清概率计算公式的来龙去脉

每一个数学概念、公式的产生都是自然的，如果我们对哪个概念、公式不理解，只要想想它产生的背景，自然就明了了。如试题第（1）问，随机变量X的分布列的得出过程并不复杂，关键是要理解随机事件、随机变量、随机变量分布列等概念及相关性质，并正确选择运算公式进行计算。

3.乐于解决实际问题，在知识的运用中加深理解各种概率模型

借助教材中“掷硬币”“掷骰子”“选手射击”等经典实例，准确区分“古典概型”“互斥事件有一个发生”“相互独立事件同时发生”等概念；清楚“超几何分布”“二项分布”“正态分布”等概率模型，以便正确选择概率公式求解。如试题第（1）问，“小明能正确回答A类问题”与“小明能正确回答B类问题”为相互独立事件，故应采用“相互独立事件同时发生”的概率乘法公式进行计算。

4.重视逻辑推理、数学运算，加强理性思维训练

逻辑推理、数学运算体现在对实际问题能进行有条理的梳理，对涉及的事件间的关系能进行清晰的辨析。如试题第（1）问，考生如果能够依据题目条件，对小明答题顺序、得分规则进行理性分析，则不仅能正确解答问题（1），问题（2）也能迎刃而解。

5.多看新闻，知晓国家大事，特别要关注经济建设和科学发展成果

宽广的视野能够消除考生对题目背景材料的恐惧感，近两年，精准扶贫、科学防疫、社会劳动实践、“一带一路”等国家时政大事都跃然卷上。同时，新高考数学试题会多方位凸显数学知识的基础性和应用性，考生只有直面各种数学应用问题，才能领会统计与概率思想在现实生活中的应用，形成自觉应用数学知识的意识，提高解决实际问题的能力。

6.平时要养成良好的书写习惯

答题时书写要有排版意识，必要的文字说明要简单明了，数学符号的表达要规范准确，对数据运算结果要有检验意识，其中，注重数学运算结果的精准性是最重要的。如试题第（2）问，计算结果支持小明选择先回答B类问题，此时他得到较高分数的可能性更大些，更有可能为团队争得荣誉。