一种加权中值滤波算法在医学磁共振图像去噪中的应用

梅玲， 苟双全

( 1.重庆水利电力职业技术学院 大数据学院， 重庆 402160；2.甘肃中医药大学(定西校区) 理科教学部, 甘肃 定西 743000 )

0 引言

医学影像图像在存储或信号传输过程中不可避免地会受到噪声影响，造成图像细节丢失，进而影响图像后续的处理效果及临床应用；因此，研究医学影像图像的去噪问题具有重要意义.为了有效消除图像中的噪声，研究人员提出了许多去噪方法，如高斯、维纳滤波、均值滤波等线性算法[1-3]和双边滤波、中值滤波、小波滤波等非线性算法[4-6].其中：线性算法可有效地抑制高斯噪声，但该算法同时也会滤掉原有图像的一些细节信息，因此使得图像变得模糊;非线性算法能较好地抑制椒盐噪声和保留图像的细节信息，但存在对高斯噪声抑制不理想的问题.由于医学影像图像常常同时受多种噪声的干扰，因此单一地使用线性或非线性滤波难以有效地抑制噪声对图像的干扰.为此，一些学者在上述算法的基础上提出了一些改进算法.例如：文献[7]提出了一种改进均值滤波算法，该方法可提高去噪性能，但存在阈值、自适应性差等问题；文献[8]提出了一种具有细节保护的自适应滤波算法，该算法能很好地保护图像的细节信息和有效地抑制脉冲噪声,并具有较强的自适应性，但其去除高斯噪声的效果并不理想；文献[9]提出了一种将中值和分数阶微分相结合的算法，该方法能有效抑制图像中的椒盐噪声和保留图像的纹理细节和边缘信息，但去除高斯噪声的效果并不理想；文献[10]提出了一种迭代中值滤波算法，该算法简单便利，可精确地恢复出被高密度椒盐噪声污染的影像细节信息,但去除高斯噪声的效果并不理想；文献[11]探讨了一种多特征融合的尺度自适应相关滤波跟踪算法，该方法对去除小噪声具有良好的准确性和稳定性，但对大噪声的抑制并不理想；文献[12]设计了一种自适应窗口形状的中值滤波算法，该方法能有效滤除图像中的噪声和保留有用信息，但计算较为复杂；文献[13]提出了一种二级修复的多方向加权均值滤波算法，该方法能有效去除高概率的椒盐噪声和保护图像边缘和细节特征，但对高斯噪声的去除效果不理想；文献[14]提出了一种基于边缘导向的非局部图像均值滤波算法，该方法具有高强度噪声环境下的图像边缘修复能力，但对图像细节的保真度较差；文献[15]提出了一种具有鲁棒性的去椒盐噪声算法，该方法能有效刻画图像的局部特征，增强图像边缘切线方向的扩散能力,但计算速度较慢.为了更好地去除医学磁共振图像中的高密度噪声和保证图像质量，本文提出了一种改进中值滤波算法，并通过仿真实验验证了该方法的有效性.

1 算法模型

1.1 均值算法模型

均值算法是一种线性滤波算法，该算法的核心思想是在图像上给定目标像素一个模板，然后用该模板中的全体像素的平均值代替原像素值.均值算法对像素点(i,j)进行平滑时，首先获取滤波窗口内所有像素的灰度均值Mean(W1[f(i,j)])， 然后以该点为中心选取一个灰度区间[W1[f(i,j)]-λ,W1[f(i,j)]+λ]， 最后将滤波窗口W1[f(i,j)]内所有灰度值处在该灰度区间的像素点进行平均，并将结果作为点(i,j)的新灰度值f1(i,j)输出[16].均值算法可有效抑制椒盐和高斯等脉冲噪声，但其去噪效果受阈值λ的影响较大.

1.2 中值算法模型

中值算法是一种非线性滤波平滑算法，它将每个像素点的灰度值设置为该点某邻域窗口内的所有像素点灰度值的中值.中值算法对噪声点进行滤波平滑时，首先在含噪的图像信号中以每个点(i,j)为中心的滤波窗口内找到该滤波窗口的灰度中值点W2[f(i,j)]； 然后对窗口内的各点均以该中值Median(W2[f(i,j)])为基准计算该点的加权系数；最后对窗口内各像素点的灰度值与相应像素权值之积求和，并将结果作为点(i,j)的新灰度值f2(i,j)输出[17].中值算法的表达式为:

(1)

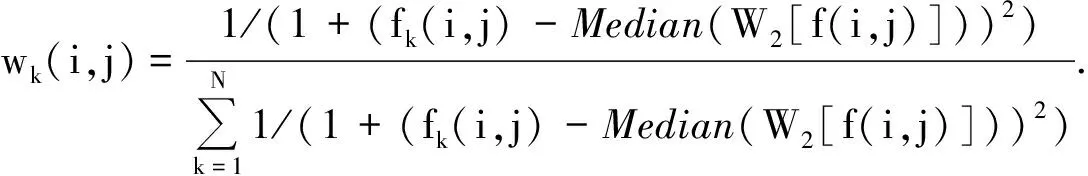
1.3 改进的中值算法模型

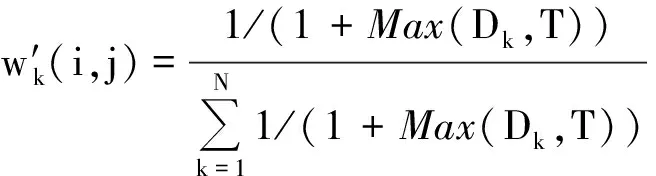
(2)

本文提出的改进中值算法流程如图1所示.

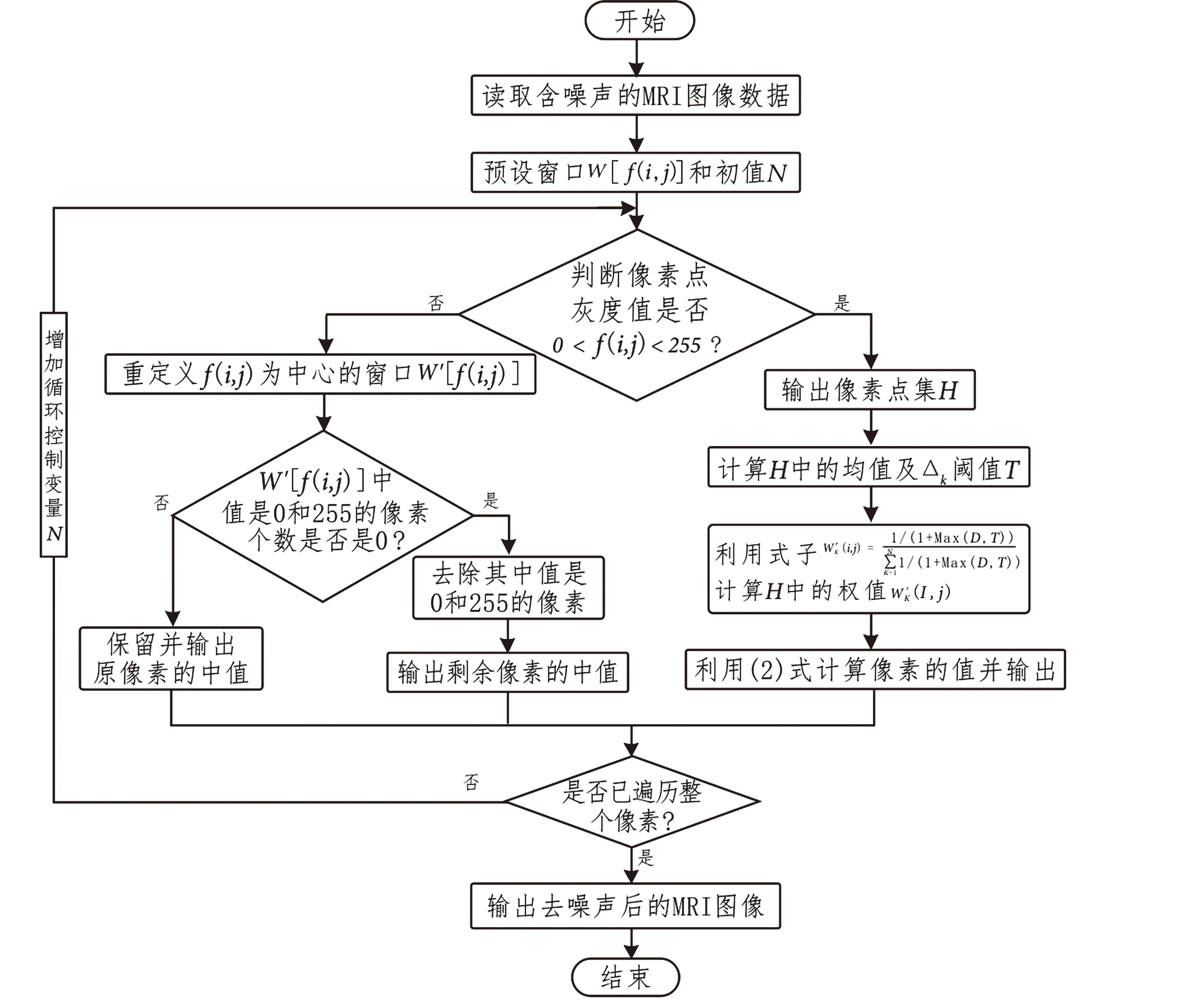
图1 改进中值算法的流程图

2 改进的中值算法在医学MRI去噪中的实现

为验证本文算法的有效性，采用Matlab仿真[18]对中值算法、均值算法和本文改进的中值算法的滤噪效果进行了对比.实验中的图像为鼻咽部的MRI， 图像中的噪声为椒盐、高斯和将这两种噪声混合的3种噪声.3种算法去噪的效果如图2 — 图4所示.

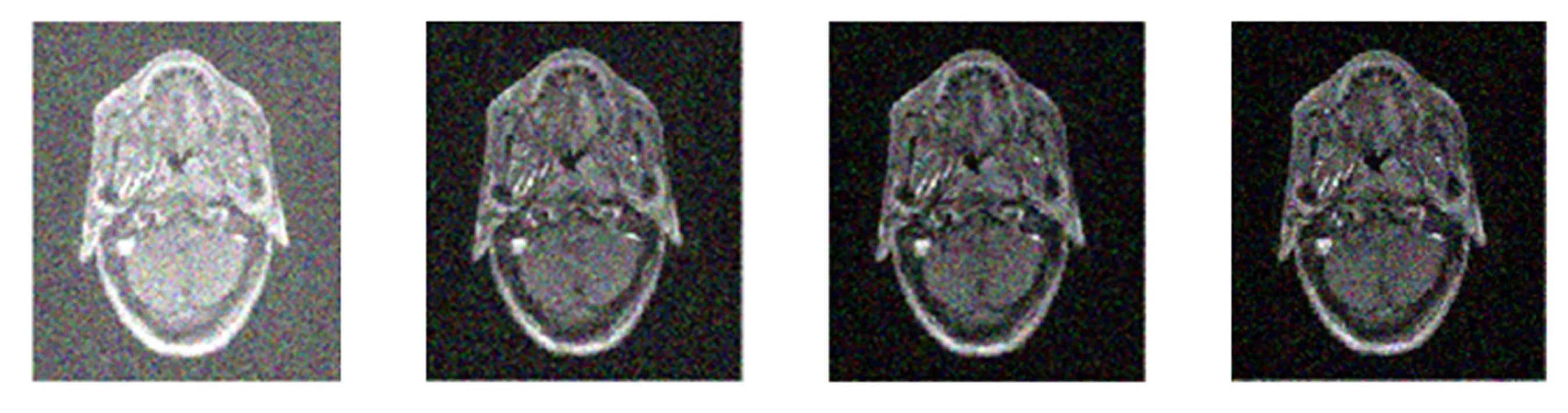
(a)高斯噪声图像 (b)中值算法 (c)均值算法 (d)本文算法 图2 3种算法对含有高斯噪声图像的滤波效果

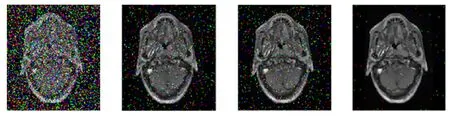
(a)椒盐噪声图像 (b)中值算法 (c)均值算法 (d)本文算法 图3 3种算法对含有椒盐噪声图像的滤波效果

(a)混合噪声图像 (b)中值算法 (c)均值算法 (d)本文算法 图4 3种算法对含有混合噪声图像的滤波效果

图2(a)是含有高斯噪声(均值为0、方差为0.3)的医学MRI，图2 (b)是对图2(a)进行中值滤波后的图像，图2 (c)是对图2(a)进行均值滤波后的图像，图2(d)是利用本文算法对图2(a)进行滤波后的图像.由图2可以看出：本文算法对高斯噪声的消除效果显著优于均值线性滤波算法和中值非线性滤波算法，且图像更为清晰.

图3(a)是含有椒盐噪声(噪声密度为0.35)的医学MRI，图3(b)是对图3(a)进行中值非线性滤波后的图像，图3(c)是对图3(a)进行均值线性滤波后的图像，图3(d)是利用本文算法对图3(a)进行滤波后的图像.由图3可以看出：本文算法对椒盐噪声的去除效果显著优于均值线性滤波算法和中值非线性滤波算法，且能够较好地保持图像的细节信息.

图4(a)是含有椒盐噪声(噪声密度为0.35)和高斯噪声(方差为0. 3)的混合噪声医学MRI，图4(b)是对图4(a)进行中值非线性滤波后的图像，图4(c)是对图4(a)进行均值滤波后的图像，图4(d)是利用本文算法对图4(a)进行滤波后的图像.由图4可以看出：本文算法对混合噪声的去除效果显著优于均值线性滤波算法和中值非线性滤波算法，且能够较好地保持图像的细节信息.

为了进一步验证本文改进算法对MRI的去噪声和保留细节信息的效果，利用峰值信噪比(PSNR)和结构相似性指数(SSIM)作为指标对均值算法、中值算法和本文算法的去噪性能进行了对比，结果见表1和表2.由表1可见，本文算法的峰值信噪比显著大于其他两种算法(高出1.5～3.6 dB)，说明本文算法的去噪性能优于其他两种的算法.由表2可见，本文算法的结构相似性指数显著大于其他两种算法(提高了5.3%～6.2%)，说明本文算法不仅能够较好地去噪，还能保持良好的结构相似性.

表1 不同算法去噪的PSNR值 dB

表2 不同算法去噪的SSIM值 %

3 结语

研究表明，本文提出的改进中值算法不仅能够有效去除医学磁共振图像中含有的各种噪声，而且还可以有效保持图像的细节信息，因此该算法在医学磁共振图像的去噪中具有良好的应用价值.本文在研究中仅对医学磁共振图像的去噪进行了研究,今后我们将利用本文方法尝试对其他医学图像(CT、DSA、超声等)进行去噪，以扩展本文方法的应用范围.