耦合腔磁系统中磁子的压缩

王根艳， 李世龑， 朱爱东

( 延边大学 理学院， 吉林 延吉 133002 )

0 引言

近年来随着对腔光力学研究的深入[1-5]，一些学者将相关研究扩展到了腔磁力学[6].腔磁系统是一种利用铁磁晶体中的集体自旋激发作为量子比特的混合量子系统[7].钇铁石榴石具有极高的自旋密度和较高的居里温度(约559 K)，可以在室温下保持良好的铁磁性质，而且在外加磁场的作用下钇铁石榴石的自旋会被集体激发而形成磁振子模式.研究显示，磁子模(Kittel模)具有相干时间长和低阻尼率以及易使腔磁系统达到强耦合机制或超强耦合机制的优点[8-11].由于钇铁石榴石球的尺寸较大，因此它在研究磁子 - 光子系统的宏观量子态方面具有天然的优势[12].压缩态在连续变量信息处理中的作用大，它不仅可以提高测量灵敏度，而且也可以用于退相干理论的研究[1].目前，已有学者利用钇铁石榴石球中的克尔非线性制备了单个磁子压缩态，但该方法需要很强的驱动场来增强克尔非线性，实验难度较大.因此，本文提出了一种利用弱压缩真空场驱动微波腔产生磁子压缩态的方法.该方法不仅可以在耦合腔磁系统中实现磁子压缩，而且可以避免由克尔非线性较弱而需要使用强驱动的问题.

1 系统模型与哈密顿量

图1为两个相互耦合的腔磁系统示意图，其中两个钇铁石榴石球被分别放置在腔模的最大磁场处，且两个钇铁石榴石球同时处于外加的均匀偏置磁场H中.图中，腔模的磁场沿x方向，偏置磁场沿z方向，两个钇铁石榴石球均由y方向的微波场驱动(图1中未画出).在均匀的偏置磁场激发下，两个钇铁石榴石球中的自旋被集体激发，尽而使得由此产生的磁子模与腔模之间存在磁偶极耦合.图中J是两个微波腔的耦合强度，κj和κmj分别是腔模j和磁子模j的耗散率(j=1，2).

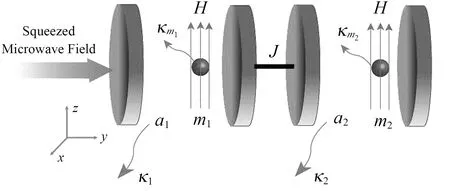
图1 耦合腔磁系统的结构示意图

由于钇铁石榴石球的尺寸远远小于微波波长，因此微波场对钇铁石榴石球的辐射压力可以忽略不计.为了方便计算，设ħ=1， 则腔磁系统总的哈密顿量为：

(1)

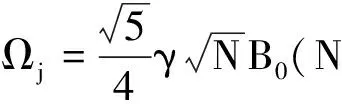
(2)

其中Δj=ωaj-ω0和Δmj=ωmj-ω0分别是腔模j和磁子模j的频率失谐.

由于系统动力学特性不可避免地会受到输入噪声和耗散的影响，因此系统的动力学演化可以用量子朗之万方程描述：

(3)

(4)

(5)

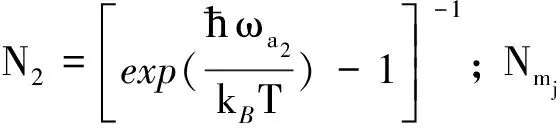
2 制备磁子压缩态

为了产生磁子压缩态，需要研究系统的量子涨落动力学.由于外部驱动场会导致腔模和磁子模的振幅增强，因此可将标准线性化技术应用于式(3)中的量子朗之万方程.因此，本文将腔模和磁子模写成经典平均值和量子涨落算符的和，即O=〈O〉+δO(O=aj,mj).在此基础上忽略二阶小量后，量子涨落满足的朗之万方程为：

(6)

实现磁子压缩态的过程为：首先利用弱压缩真空场驱动共振腔模1， 以此对磁子模1进行压缩；然后通过超导传输线的耦合作用将压缩转移到腔模2上；最后通过磁偶极子作用将压缩转移到磁子模2上，以此实现磁子模2的压缩.为方便起见，本文引入腔模和磁子模的振幅正交分量算符及其相应的输入噪声算符：

(7)

(8)

利用式(7)和式(8)可将方程(6)简化为：

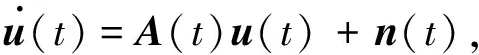
(9)

其中u(t)是涨落算符的列矩阵，n(t)是输入噪声算符的列矢量，A(t)是漂移矩阵，并且

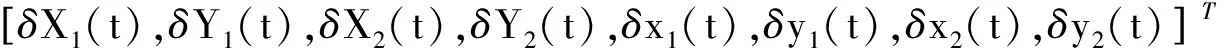
(10)

由于本文使用的是非线性化的量子朗之万方程，因此系统在时间演化过程中其输入态的高斯性质保持不变，且系统的量子涨落为四模高斯态；因此，可用8×8协方差矩阵的矩阵元定义量子涨落的时间演化，即Vk,l(t)=〈Uk(t)Ul(t)+Ul(t)Uk(t)〉/2 (k,l=1,2,…,8).当系统处于稳态时,矩阵V(t)满足李雅普诺夫方程[15]：

A(t)V(t)+V(t)AT(t)=-D,

(11)

其中与噪声相关的扩散矩阵D是由〈nk(t)nl(t′)+nl(t′)nk(t)〉=2Dk lδ(t-t′)定义的，D=D1⊕D2，

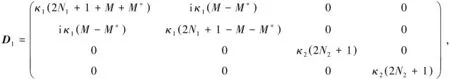
(12)

D2=diag[κm1(2Nm1+1),κm1(2Nm1+1),κm2(2Nm2+1),κm2(2Nm2+1)].

(13)

由劳斯 - 霍尔维茨判据[16]可知，如果漂移矩阵A(t)的所有特征值都有负实部，则系统将达到稳态.

3 数值模拟分析和讨论

从式(11)可以看出，V(t)的对角线元素是腔和磁子的振幅正交分量的方差，其方差为〈δZ2(t)〉 (Z=Y1,X2,x1,y2).当〈δZ2(t)〉<〈δZ2(t)〉ZPF(〈δZ2(t)〉ZPF= 0.5是零点涨落)时，腔和磁子可以产生压缩态，并且方差越小量子涨落越小.腔和磁子压缩程度用分贝(dB)表示，即-10 lg(〈δZ2(t)〉/0.5)， 由此可知压缩度的值越大压缩态的噪声越小.

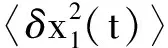
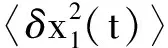
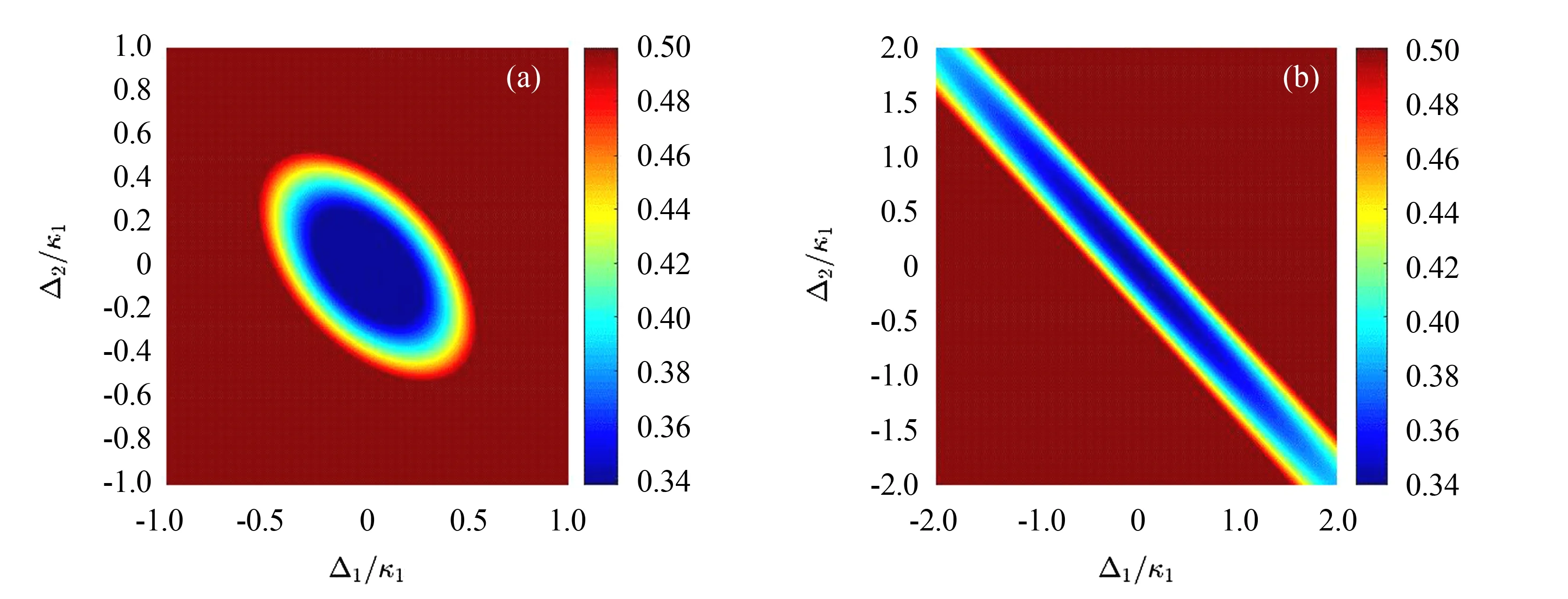
图和随腔失谐的变化情况

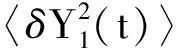
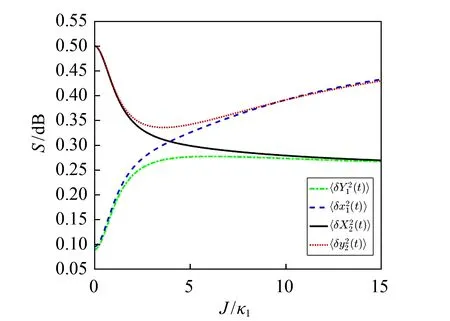
图4 腔和磁子的振幅正交分量的方差S随光子耦合强度J的变化情况

为了验证腔压缩态和磁子压缩态对环境温度具有鲁棒性，绘制腔和磁子的振幅正交分量的方差S随温度T的变化关系图，如图5所示.图中Δ1=Δ2=0， Δm1=Δm2=0， 其他参数见图2.由图5可以看出，当温度达到0.196 K时磁子2仍然处于压缩态，这表明磁子2的振幅正交分量的方差S对环境温度具有很好的鲁棒性，且腔压缩态和磁子1压缩态对环境温度也具有很好的鲁棒性.

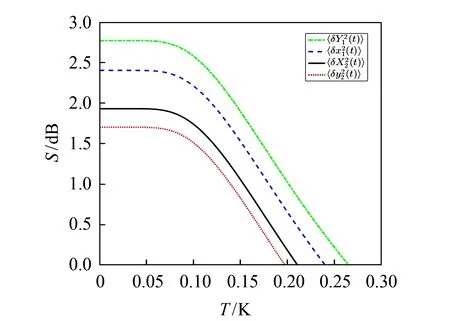
图5 腔和磁子的振幅正交分量的方差S随温度T的变化情况

4 结论

本文采用一个弱压缩真空场驱动微波腔产生了两个磁子的压缩态.数值模拟结果表明：选择合适的模间相互作用，可以制备两个磁子压缩态，并且在失谐量满足Δ1=Δm1=Δ2=Δm2=0时，磁子1和磁子2的振幅正交分量的方差分别达到0.287和0.338.同时，腔压缩态和磁子压缩态对环境温度具有很好的鲁棒性.本文结果可对宏观量子态的研究提供参考.