基于FSC-MPE与BP神经网络的滚动轴承故障诊断方法
刘俊锋,董宝营,俞翔,万海波
1 海军工程大学 动力工程学院,湖北 武汉 430033
2 中国人民解放军91278部队,辽宁 大连 116041
3 海军工程大学 舰船与海洋学院,湖北 武汉 430033
0 引 言
滚动轴承是旋转机械设备的重要零部件,对滚动轴承的运行状态进行监测并进行早期的故障诊断具有重要意义[1]。
轴承故障振动信号主要包括由故障本身产生的周期性冲击振动成分和由冲击作用诱发的轴承系统的高频固有振动成分,在实际测试中,低频部分由于其强背景噪声,信噪比较低[2]。小波变换[3](wavelet transform, WT)、经验模态分解[4-5](empirical mode decomposition,EMD)、集成经验模态分解[6](ensemble empirical mode decomposition,EEMD)和变分模态分解[7](variational mode decomposition,VMD)等分解重构方法虽然能够有效分离信号与噪声,提取出部分故障特征,但也会导致信号局部信息失真和细节丢失,同时,还需要人为选取本征模函数。随着神经网络在故障诊断领域的深入发展,将信号处理方法与神经网络相结合的智能故障诊断技术取得了众多成果。王海龙等[8]、何江江等[9]和吕阳等[10]分别将EMD,EEMD和VMD方法与神经网络相结合,对滚动轴承故障诊断进行了研究,但结果显示,EMD存在着模态混叠现象,无法正确分离频率相近的分量等,VMD则存在边界效应,需要预先定义模态数[11]。
滚动轴承具有周期运动的特点,且由其故障产生的冲击也呈周期性。Gardner等[12]基于周期平稳信号研究提出了谱相干理论,之后,该理论被引入故障诊断领域。Antoniz等[13]提出一种快速谱相关(fast spectral correlation,FSC)分析方法,解决了传统谱相关分析计算效率较低的问题。为了量化由FSC分析所提取的滚动轴承故障特征在多尺度下的变化情况和复杂性并提高计算效率,引入了多尺度排列熵(multiscale permutation entropy,MPE)[14]量化故障特征。
本文拟针对滚动轴承早期故障识别困难的问题,提出一种基于FSC-MPE与BP神经网络的故障诊断方法。首先,利用FSC分析提取原始振动信号的故障特征,然后,利用MPE对故障特征进行量化,最后,将故障特征数据输入BP神经网络进行故障诊断模型训练与测试,以证明基于FSCMPE与BP神经网络的滚动轴承故障诊断方法的可行性和优越性,为滚动轴承健康状态评估提供技术支持。
1 理论分析
FSC算法对于复杂信号中的周期性成分具有增强的作用,通过增强包络谱分析,可以对滚动轴承的冲击性故障进行直观表征,BP神经网络具有非线性映射能力强、结构清晰、使用简便等特点[15-16]。而FSC与MPE相结合的故障特征提取算法在处理循环平稳信号时具有明显的效率优势,并且可以极大地缓解神经网络的计算压力,这与需要大量数据样本进行学习训练的神经网络故障诊断系统十分契合。针对非平稳工况下等角度采样存在频谱分析模态混叠等问题,可以采用等角度重采样方法将信号变换到角域。基于FSC-MPE与BP神经网络的滚动轴承故障诊断流程如图1所示。
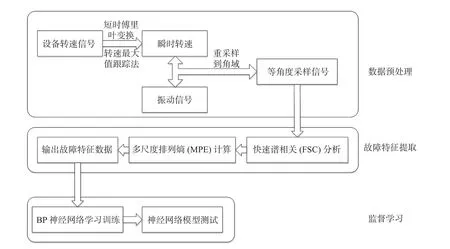
图1 轴承故障诊断流程Fig.1 Process of bearing fault diagnosis
1.1 FSC分析
Antoniz等[13]于2017年提出FSC分析算法,并提供了可观的计算增益,使其在分析宽周期频率范围内的周期性平稳信号时非常实用。通常,采用循环自相关函数来了解滚动轴承的二阶循环平稳信息。针对循环平稳信号x(tn)(tn为 第n个采样点时间),循环自相关函数(τ)的定义为:
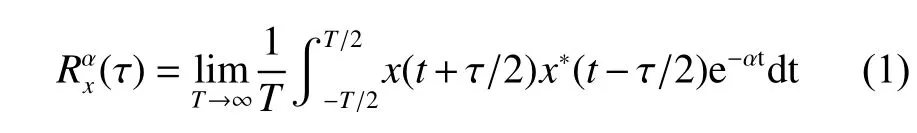
式中:α为循环频率;x为循环平稳信号;τ为延迟时间;T=(2N+1)T0, 其中T0为 周期,N代表x(tn)周期长度,周期延拓后趋于∞;t为采样时间;*表示复共轭。
基于循环自相关函数,得到其谱相关SCx(α,f)的定义为:
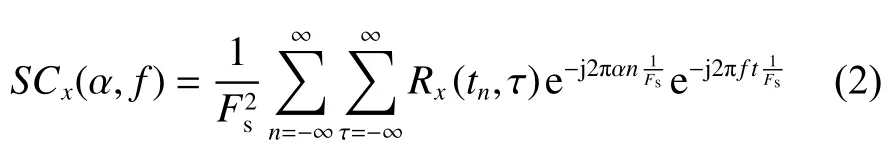
式中:Fs为 采样频率;tn=n/Fs,其中n为第n个采样点;f为信号频率。谱相关分析被定义为瞬时自相关函数的双重离散傅里叶变换。
在快速谱分析中引入短时傅里叶变换(short time fourier transform,STFT),可以极大地提升运算速率。对信号x(tn)进行短时傅里叶变换,定义如下:
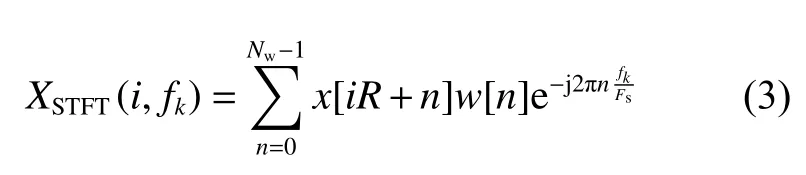
式中:XSTFT(i,fk)为 信号x(tn)的短时傅里叶变换;Nw为STFT的窗长;R为 STFT的块位移;w(n)为窗函 数;x[n]为x(tn) 的 改 写 形 式;fk=k∆f,其 中k=1,2,···,Nw−1, 为离散频率, ∆f=Fs/Nw,为频率分辨率;i为窗函数移动次数。
对STFT进行相位校正,其定义为:
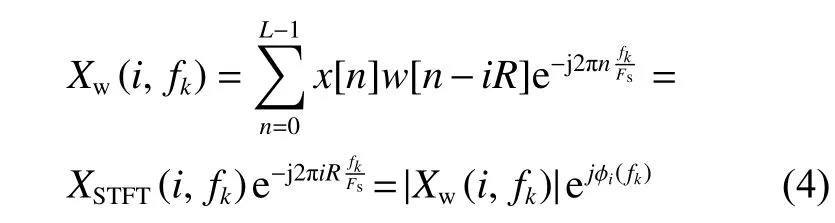
式中:Xw(i,fk)为 信号x(tn)在iR/Fs处 的复包 络,其模的平方 |Xw(i,fk)|2为频带的能量流;L为信号长度;ϕi为相位,为其导数。
近似地认为 α=p∆f+δ (这里p为最接近给定循环频率α的STFT频率指数,δ为残余量),同时,取一阶泰勒展开得ϕi(fk−α)≃ϕi(fk−p∆f)−δ·(fk−p∆f), 其 中(fk−p∆f)≃−2π(iR+N0)/Fs,当Nw为 偶 数 时,N0=Nw/2; 当Nw为 奇 数 时,N0=(Nw+1)/2。则上式可改写为
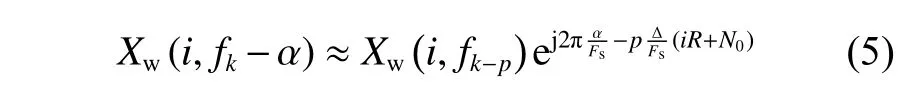
基于STFT的循环谱相关计算流程为:
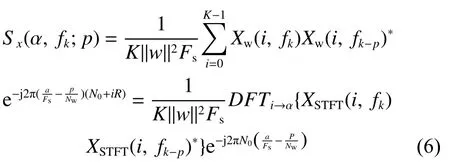
式中:S x为扫描谱相关;DFT为离散傅里叶变换;w为窗函数;K=(L−Nw+R)/R。
当p≠0时,信号x(tn)的周期为T,循环频率α=1/T,能量X[w(i,fk)Xw(i,fk−p)∗在]频带[fk−p−∆f/2,fk−p+∆f/2]和fk−∆f/2,fk+∆f/2内流动;当p=0时,能量在[fk−∆f/2,fk+∆f/2]内周期性流动。
快速谱相关的定义为:
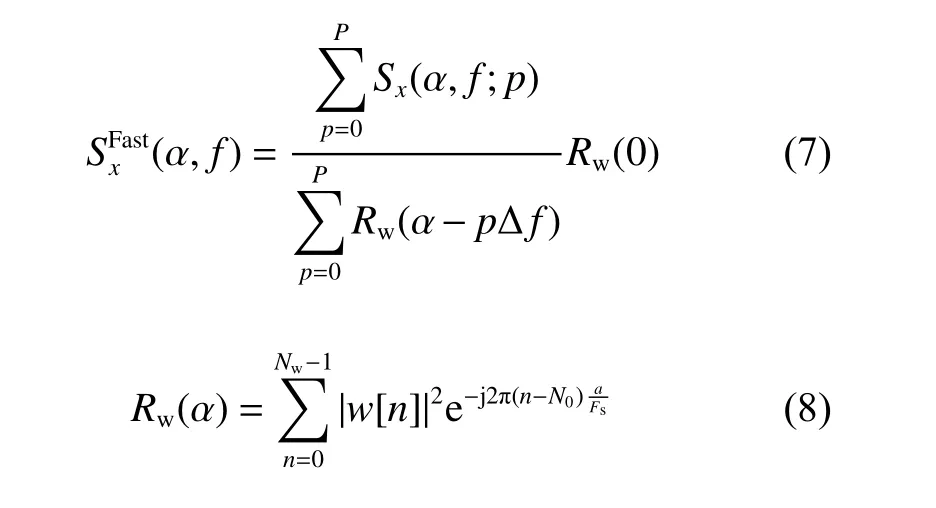
式 中:P为p的 最 大 值;Rw(α)为 核 函 数,且Rw(α)=//w//2。
由FSC分析,可以推导出FSC函数,其定义为:
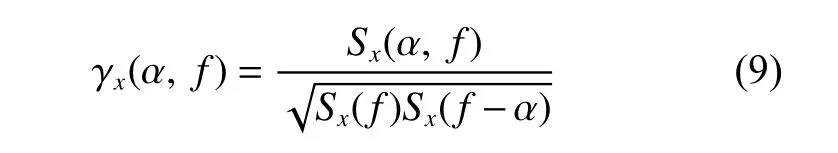
增强包络谱(EES)的定义为:
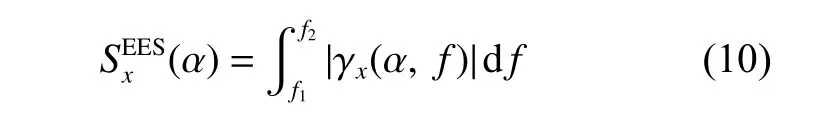
1.2 MPE
Aziz等[17]提出 了MPE概念,并克服了排列熵只在单一尺度上衡量时间序列复杂性的局限性。通过粗粒化时间序列获取不同时间尺度下的排列熵,能够更加全面地表征信号的复杂程度和变化程度[14]。MPE的计算主要分为求粗粒化时间序列和计算排列熵2个部分。
1) 待分析的时间序列为y(k)=(x1,x2,x3,···,xN),其中k=1,2,···,N,经粗粒化处理后,得到粗粒化序列 {y},其表达式为:
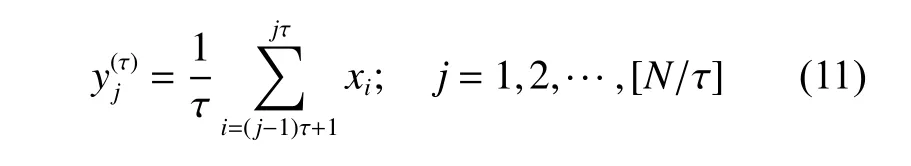
式中, [N/τ]为 对N/τ 取整,其中 τ=1,2,···,τ为尺度因子,当 τ≥2时,粗粒化才有意义,原始序列被粗粒化为长度为 [N/τ]的粗粒信号。尺度因子的取值需保证粗粒化序列长度不影响熵值的计算,在本文中,为保证效率与数据量的充分度,选取 τ=20。
2) 分别计算每个粗粒化序列的排列熵,由此即可获得MPE结果。计算MPE还需要考虑合适的嵌入维数m,若m的取值太小,频带熵值会随尺度因子 τ的增大而变化过小,但m的取值越大,计算耗时将越长,本次研究选取m=5。
1.3 BP神经网络
BP学习算法是研究最深入、运行机制最简洁、使用最为广泛的一种人工神经网络。BP神经网络由输入层、隐蔽层和输出层组成,包含前馈计算过程与误差反向传播过程[18]。本文将引入BP神经网络对由FSC-MPE分析得到的轴承故障特征进行模式识别,典型的三层BP神经网络拓扑结构如图2所示。图中,输入向量为X=(x1,x2,···,xn)T,输出向量为Y=(y1,y2,···,yl)T;网络输入层有n个神经元,隐藏层有s个神经元,输出层有l个神经元;wi j为输出层第i个神经元与隐藏层第j个神经元之间的连接权值;wjk为隐藏层第j个神经元与输出层第k个神经元之间的连接权值。
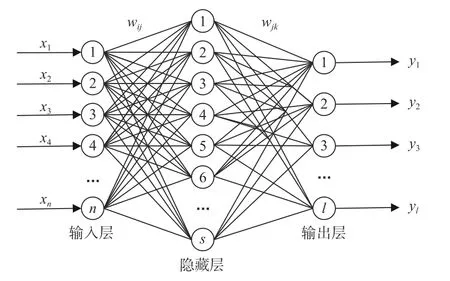
图2 BP神经网络拓扑结构图Fig.2 Topology diagram of BP neural network
在BP神经网络前馈计算过程中,从输入层开始依次计算各层的输入与输出,将最后从输出层输出的结果输入SoftMax分类器,并使用交叉熵损失函数(cross entropy error function)计算输出结果与目标结果的损失。然后,通过梯度下降算法调整各层神经元之间的连接权值,使其损失函数往减小的方向变化。以隐藏层到输出层的调整为例,其权值修正公式为:
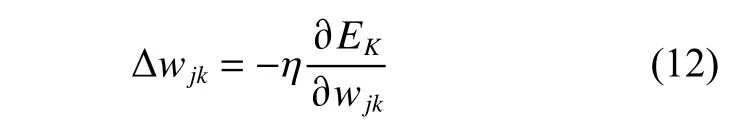
式中:η为学习率;EK为网络的均方误差,其中K代表训练周期数。
2 基 于FSC-MPE的 滚 动 轴 承 早 期故障特征提取
2.1 轴承故障模拟
针对轴承故障模拟平台的实验轴承进行故障诊断,设备如图3所示。轴承的型号为NSK7010C,其外径80 mm,内径50 mm,接触角15°,滚动体直径8.7 mm,共19个滚动体。轴承故障为人工模拟故障,在内、外圈激光加工了一个平行于轴承轴线、宽0.5 mm、深0.5 mm的槽,轴承故障特征阶次为8.33阶。电机工况为:平均转速3 000 r/min,振幅300 r/min。在测试过程中安装转速传感器,同时在轴承基座上安装振动加速度传感器,采样频率为65 536 Hz。

图3 轴承故障模拟试验台Fig.3 Bearing fault simulation test stand
2.2 瞬时转速与等角度采样信号
本次实验设置为非平稳工况,由于传感器采样为等时间间隔采样,旋转一圈采集的数据点存在较大波动,故直接进行频谱分析存在模态混叠等问题[19]。所以,首先结合转速信号对轴承振动信号进行预处理,将其从时域变换到角域。选取采样时长为4 s的转速信号与基座振动加速度信号,对转速信号进行短时傅里叶变换,结果如图4(a)所示。已知电机转速在3 000 r/min上下浮动,利用最大值跟踪方法求出转频[20],结果如图4(b)所示。通过瞬时转速,建立采样时间与采样相位的对应关系,并将此关系代入振动信号,然后将非平稳的时域振动信号变换到角域,使其变成周期平稳的等角度采样信号,结果如图4(c)所示。
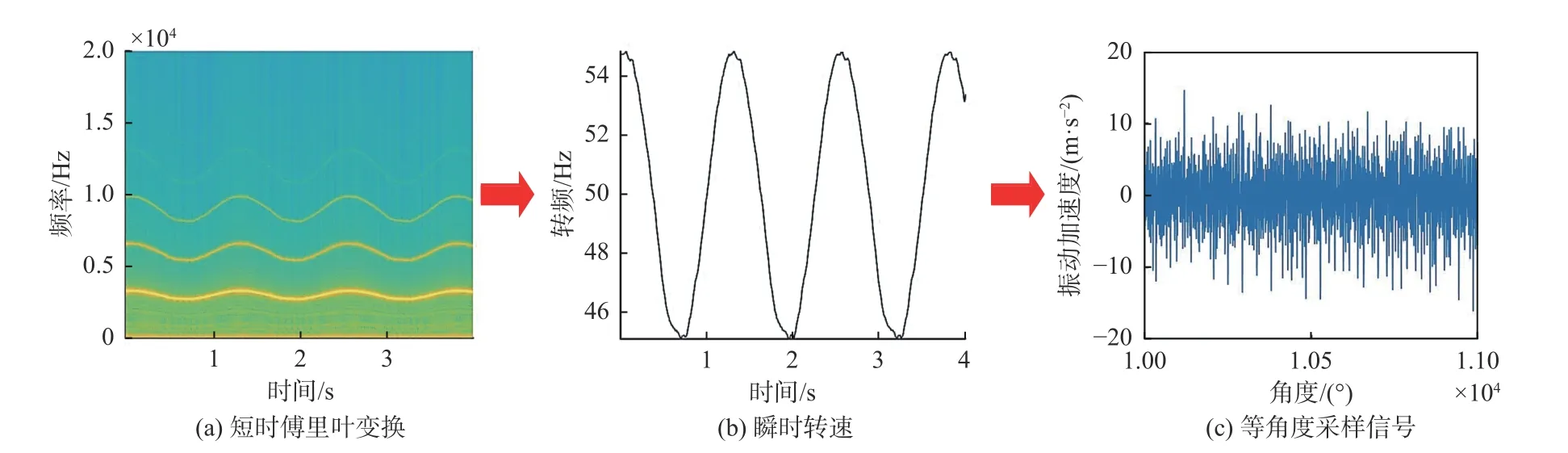
图4 非平稳振动信号预处理Fig.4 Non-stationary vibration signal preprocessing
2.3 FSC-MPE分析
对周期平稳的等角度采样信号进行FSC分析,得到其谱相关分析结果如图5所示,并求其增强包络谱,结果如图6所示。

图5 快速谱相关分析Fig.5 Fast spectral coherence analysis
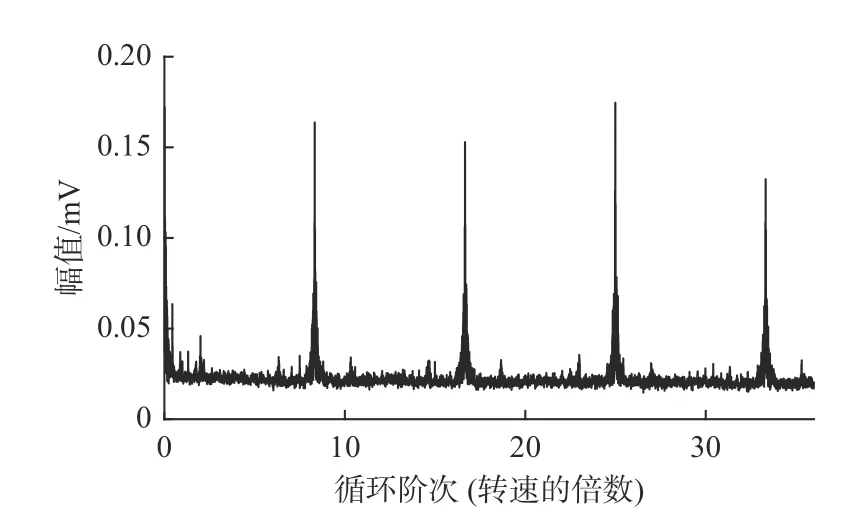
图6 增强包络谱Fig.6 Enhanced envelope spectrum
图6证明,轴承振动信号中存在基频为8.33倍转频的周期性振动成分,8.33阶正好为轴承故障特征阶次。由此推论,轴承内、外圈上存在故障,并使得振动信号中混入了冲击信号成分。通过FSC分析,可以得到明显且直观的故障特征,相较于小波变换、EMD等方法,其效果较直观,如图7所示。
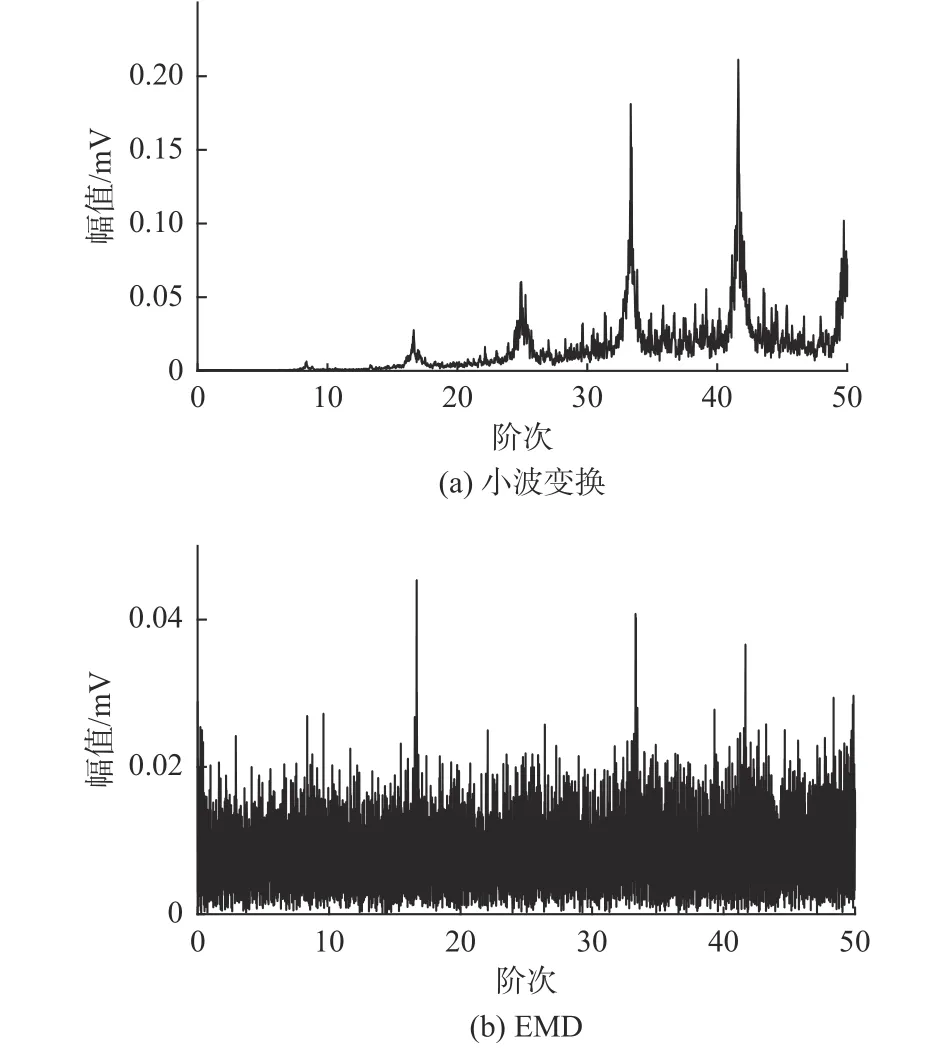
图7 离散小波变换和EMD得到的故障特征Fig.7 Fault characteristics obtained by discrete wavelet transform and EMD
如果直接将大数量样本的增强包络谱输入神经网络进行故障诊断,计算量会很大。所以,本文将采用MPE算法对故障特征进行量化,从多尺度的角度深入挖掘目标序列变化信息,这样可以极大地缓解神经网络的计算压力并有助于实现智能化故障诊断。
3 FSC-MPE与BP神经网络相结合的故障模式识别
3.1 轴承故障数据预处理
FSC-MPE算法具有效率高、可靠性强、适应性强的特点,易于处理大批量数据,与神经网络十分契合。BP神经网络具有优异的非线性映射能力和泛化能力,对于复杂的轴承故障分类问题,效果较好。为了验证本文所提方法,采用美国凯斯西储大学(CWRU)开放轴承数据库的样本数据进行了试验分析,轴承故障试验台如图8所示。

图8 CWRU轴承故障试验台Fig.8 Bearing failure test stand of CWRU
本文以驱动端轴承(6205-2RS JEM SKF)为研究对象,选取负载为745.70 W、转速为1 772r/min工况下的测量数据进行分析。加速度传感器被放置在电机外壳的驱动端和风扇端的12点钟位置,采样频率为48 kHz。本文考虑了7种典型的故障类别,如表1所示,包含正常情况、内圈故障和外圈故障3类情况。其中,故障情况又分别包含损失直径为0.07,0.14,0.21 in这3种故障程度,其故障特征阶次如表2所示。每类故障包含150个样本,其中训练样本125个,测试样本25个。
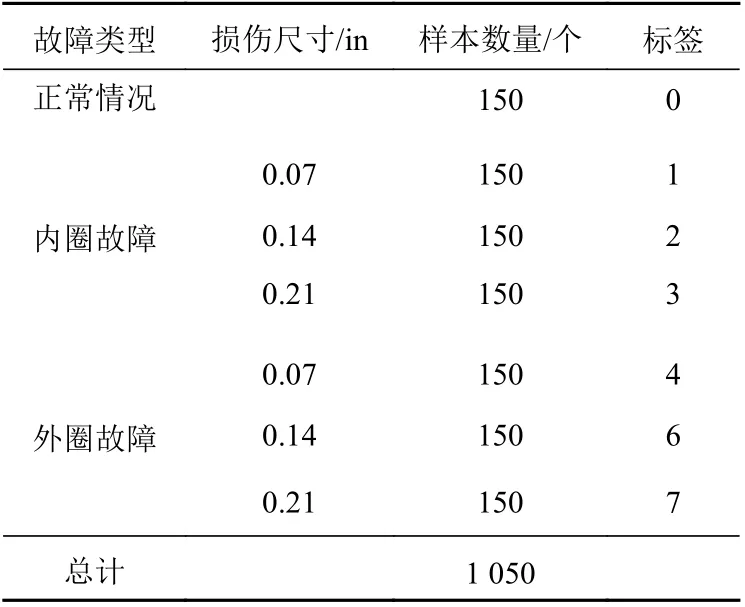
表1 轴承数据样本统计Table1 Sample statistics of bearing data

表2 故障特征阶次Table2 Fault defect frequencies
将上述样本数据进行FSC分析获取其故障特征,其增强包络谱如图9所示。
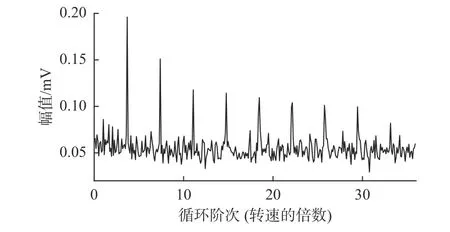
图9 试验轴承振动信号增强包络谱Fig.9 Enhanced envelope spectrum of vibration signal of test bearing
通过FSC分析得到轴承故障特征后,接下来,将通过MPE对获取的故障特征进行量化。MPE的尺度因子τ=20,嵌入维数m=5。MPE能够在不同尺度情况下深入挖掘数据变化信息,实现对轴承故障的特征量化。经过处理,每个轴承的故障数据样本变为 [1×20]的一维向量。
3.2 BP神经网络故障模式识别
将故障特征向量分为训练集和测试集,针对每类故障训练集的样本数量为125个,测试集的样本数量为25个,在实际工作中,数据集可以不断补充。研究表明,含有3层隐层的BP神经网络具有极强的非线性拟合能力,增加隐层可以提高精度,但同时也会增加计算量。本文选取具有5层隐层的神经网络,采用随机梯度下降(SDG)的优化算法进行反向传播计算。损失函数与测试集故障识别的准确率随迭代次数增加的变化情况如图10所示.
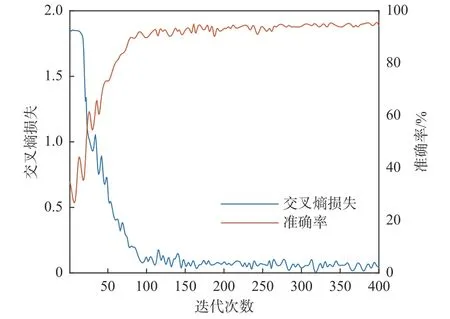
图10 神经网络交叉熵损失与测试集识别准确率Fig.10 Accuracy of neural network cross entropy loss and test set recognition
最终,经过多轮训练后,BP神经网络内部参数会趋于稳定,识别的准确率也趋于平稳。神经网络对各类别故障的识别情况如图11所示,将该识别结果进行统计,结果如表3所示。经统计,BP神经网络对各类别轴承故障识别的准确率均在96%以上,总体识别准确率为97.71%,在样本种类与数量充足的情况下,准确率还可以进一步提升。
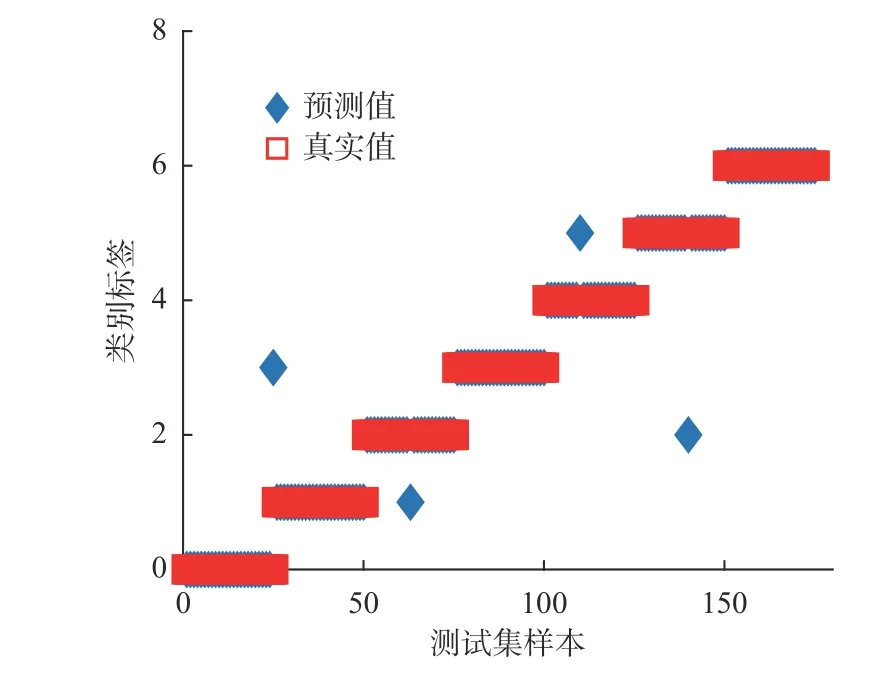
图11 测试集各类别故障识别结果Fig.11 Various fault identification results of test sets
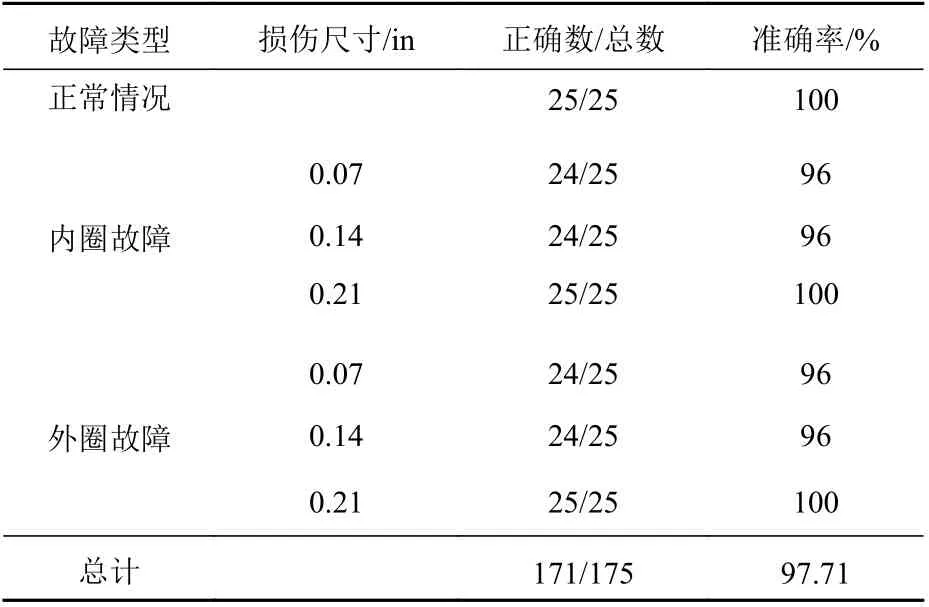
表3 轴承故障诊断结果Table3 Diagnosis results of bearing fault
4 结 论
本文提出了一种基于FSC-MPE与BP神经网络相结合的滚动轴承故障智能诊断方法。针对原始振动信号,融合了预处理、故障特征提取和模式识别流程,在一定程度上实现了端对端的滚动轴承故障诊断。相比传统的滚动轴承故障诊断方法,本文方法具有以下主要优势:
1) 通过FSC-MPE算法,可以更好地表征轴承的故障特征并进行量化,能极大地缓解神经网络的计算压力,提高故障诊断效率。
2) BP神经网络的鲁棒性可以随着数据种类和数据量的增加而提高,相应的故障诊断准确性也会得到发展。将FSC-MPE方法与BP神经网络相结合,可为大数据故障样本下从强背景噪声、非平稳的滚动轴承故障振动信号中提取出故障特征并进行故障模式识别提供新的思路。

