基于SAC算法的作战仿真推演智能决策技术

王兴众，王敏，罗威

中国舰船研究设计中心，湖北 武汉 430064

0 引 言

人工智能技术的快速发展正在加速战争形态的演变，军事智能化已成为新一轮军事变革的核心驱动力[1]。认知速度是智能时代制胜之道的根本。在认知域，自主决策将逐步取代辅助决策。在认知战这种全新智能化战争需求推动下，智能决策问题亟待解决。作战仿真推演系统是体系作战的重要决策判断工具，利用从战争或军事训练中抽象得到的作战规则，对战场环境、军事力量、作战行动等要素进行形式化描述和建模，依据模型，推演分析作战过程及其结果和伤亡等情况，是军队开展模拟训练、科学评估作战预案的有效途径。一旦认知战成为未来体系对抗的主战场，仿真推演系统将成为研究对抗战术的虚拟战场，而智能决策则是影响战争走向的机关枢纽[2]。

传统的作战推演决策主要依靠固化在模型中的决策部件，它可直接实现仿真模型对战场态势的理解，输出对应的决策方案[3]。而外部决策模型则是与之相对的另一种传统决策建模方法，其将指挥员的决策知识和判断经验录入知识库，作为该模型进行仿真推演的依据，例如基于规则和条件的决策建模方法。但是，一旦状态空间规模增加，上述决策方法将难以维护，而行为树的模块化和可复用性使其可成为了强有力的决策工具[4]。2017年4月26日，美国国防部率先提出成立“算法战跨功能小组（AWCFT）”，以推动人工智能和大数据等技术加速融入军事领域，正式开启了认知智能军事化应用探索的进程。2019年12月31日，美国智库“战略与预算评估中心(CSBA)”发布了《夺回海上优势：为实施“决策中心战”推进美国水面舰艇部队转型》的报告，指出“决策中心战”作战概念将成为美军智能化转型建设的理论牵引。为此，国内也在积极开展相关研究。国防科技创新特区于2018年起举办了战术级别的“先知兵圣”人机对抗挑战赛，对抗双方基于“兵棋陆战”平台，在城市和山地等多地形、多地貌虚拟场景下进行自主推演、决策执行和“夺控点”的争抢，最终以双方对抗的胜负来评估相关人工智能算法在作战决策中的影响程度。

军事对抗面临的突出问题是规则不完备、信息不完全、响应高实时等，而强化学习（RL）中的智能体在与环境交互过程中可以不断试错，以最大化累积回报作为目标，不断探索最优策略，展现出强大的决策力，这为解决上述问题提供了新的有效途径。例如，利用残差网络(ResNets)与蒙特卡罗搜索树(MCTS)[5]相结合的方式建立决策模型，采用单智能体对回合作战进行决策，使兵棋推演系统具备智能决策能力。然而，机器学习方法一般普遍存在的问题是模型过拟合、泛化能力差；因此，基于深度强化学习(DRL)的智能决策框架成为了研究热点。利用深度学习（DL）算法分析处理战场感知数据，有助于指挥员迅速辨别战场态势；利用RL算法进行辅助决策，有利于提高指挥员的谋略水平，夺取竞争性优势[6]。未来战争的作战模式是“以快吃慢”，决策模型的策略输出速度同样不容忽视。压缩网络结构（例如采用参数修剪和低秩分解等方法[7]）将深度网络变为轻量级网络，以满足实际作战响应高实时的特点。

目前，针对决策空间巨大、信息不完全的智能策略对抗技术尚未完全取得突破，基于DRL的理论与方法仍处于起步阶段。面对作战需求，决策优势是核心，其将成为现代战争制胜的关键，在OODA（观察、判断、决策、行动）环路中，决策还是制约循环速度的瓶颈。鉴此，本文将主要从智能决策模型构建角度，研究将深度神经网络（deep neural network ）与SAC（soft actor-critic）强化学习算法应用于作战仿真推演系统的途径，以及应用仿真推演平台，以舰载直升机反潜想定为例，验证决策模型的有效性和相关算法的适用性。

1 SAC算法

SAC算法[8]包含3个关键要素：1）利用最大熵框架增强模型的稳定性，并提高智能体的探索能力；2）采用离线策略更新，重复利用先前收集的数据，提高效率；3）基于actor- critic (AC) 体系结构，其策略网络与价值网络相互独立，将策略称为Actor，价值函数称为Critic。

1.1 最大熵强化学习

马尔科夫决策过程（Markov decision process，MDP）是强化学习问题在数学上的理想化形式[9]。用五元组 (S,A,P,r,γ)定义无限视界MDP，其中：S为状态空间，A为动作决策空间，二者的空间连续；P:S×S×A→[0,∞)，为状态转移概率，表示在给定当前时刻的状态st∈S和探索动作at∈A时，转移到下一时刻状态st+1∈S的概率密度；γ为折扣因子，表示每个时刻获得的收益对总回报的影响程度；r为每次状态转换环境给予的有界回报，r:S×A→[rmin,rmax]。

智能体的目标是学习一种策略 π:S→A，使累积期望回报值最大化，如式（1）所示。

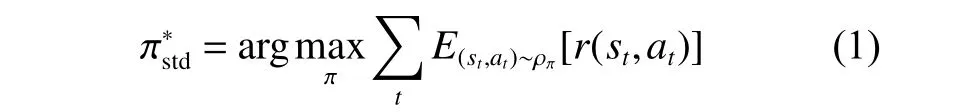
式中，ρπ为策略生成的轨迹(st,at,st+1,at+1,st+2,at+2,···)的边缘分布。

如式（2）所示，最大熵强化学习是在式（1）的基础上增加了可调整熵值项H，智能体的目标变为寻找令累积期望回报和熵值同时最大化的最优策略。信息熵越大，说明分布越均匀。最大化信息熵，有利于增加模型的探索能力。

式中，α为温度参数， α→0时，式（2）等同于式（1）。

1.2 离线策略更新

离线策略更新采用两个策略，一个策略用于智能体学习，并最终成为最优策略，称为目标策略πtar；另一个策略用于生成智能体轨迹样本，称为行动策略πact。此时，由于智能体用于学习的数据与待学习的目标策略相互分离，因此离线策略更新一般方差大且收敛慢。但是，这种分离的优点在于，当行动策略对所有可能的动作继续进行采样时，可以采用确定性的目标策略。

在处理预测问题时，目标策略和行动策略固定，旨在学习状态价值函数vˆ≈vπ（ 给定策略π的状态价值函数）或动作价值函数qˆ≈qπ（ 给定策略π的动作价值函数）。对于控制问题，两个策略在智能体学习过程中会不断变化，目标策略πtar逐渐变成关于qˆ的 贪心策略，而行动策略πact逐渐变成关于qˆ的某种探索性策略。

1.3 AC体系

AC体系采用时序差分（TD）的方法，使用独立的模型估计状态−动作序列的长期回报，而非直接采用真实回报。如图1所示，策略网络被称为Actor，用于动作选择；价值网络称为Critic，用于评估动作的优劣。采用式（3）所示的TD形式来评估最新选择的探索动作at， 其中V为Critic的状态价值。若TD误差（即δt）为正，则应加强选择探索动作at的趋势；若TD误差为负，则应降低选择探索动作at的频率。

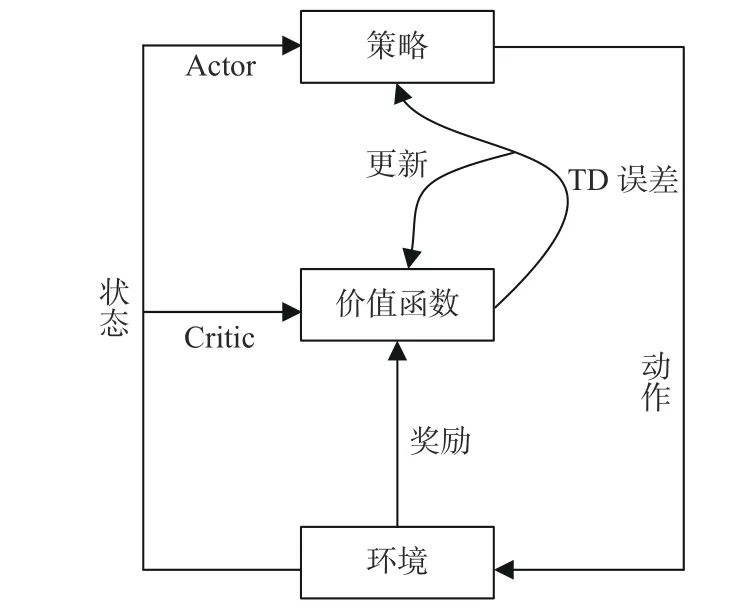
图1 AC体系架构图[10]Fig.1 The architecture of Actor-Critic[10]

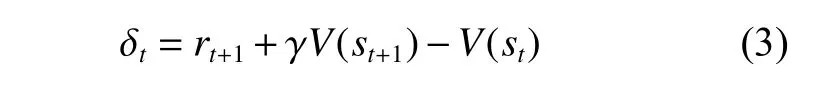
式中，rt+1为下一时刻环境给予的回报值。

如图2所示，采用离线策略更新的AC体系由在线评估网络和目标网络构成，网络结构和初始化参数均相同。首先，提取经验缓存数据，通过目标网络得到目标回报值；然后，根据TD误差更新评估网络中的Critic网络；最后，更新评估网络中的Actor网络，其中动作的探索和Actor网络的更新分别采用不同策略。

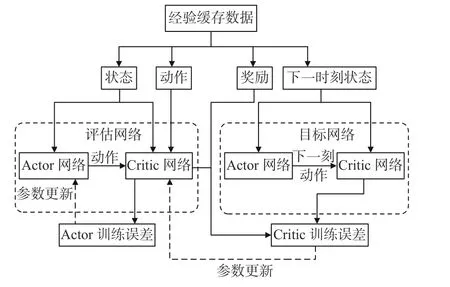
图2 采用离线策略更新的AC体系Fig.2 AC architecture updated by off-policy

2 仿真推演任务分析

2.1 反潜想定介绍

导弹驱逐舰搭载直升机反潜想定设定的场景如下：蓝方海军有2艘潜艇停泊在某海域，红方海军得到情报，派遣舰载反潜直升机（以下称反潜机）前往搜寻蓝方海军的潜艇。红方海军反潜机的作战目标是通过在目标水域投放声呐浮标，发现并摧毁蓝方潜艇，其水面舰船主要为反潜机提供鱼雷和反潜火箭弹等武器支援。而蓝方海军潜艇的作战目标是隐藏航迹，避免被消灭。红蓝双方海军的兵力编成如表1和表2所示。

表1 红方海军兵力编成Table1 The navy strength of red team

表2 蓝方海军兵力编成Table2 The navy strength of blue team

2.2 声呐浮标建模

声呐浮标系统按直线通路探测、水面反射探测和汇聚区探测依次进行判断。以9.874 73 n mile为直线探测距离基数，根据敌我深度d、目标所处海底地形m和目标距海底高度h，修正得到直线探测距离RD，如式（4）所示。

式中，以声呐最大理论探测距离为基数，根据d，m，h和探测方速度v及目标信号特征强度Ts，修正得到汇聚区的有效探测范围RC，如（5）式所示。

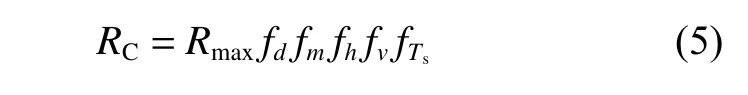
式中，Rmax为声呐的最大理论探测距离。通常，直线探测距离远大于汇聚区探测范围，即RD≫RC。式（4）与式（5）中f均为与变量相关的修正系数。

对于水面反射，如图3所示，设探测点和目标点距海底高度分别为a和b，计算声波通过水面反射的位置，该位置与探测点的水平距离为w，探测点与目标点的水平距离为c，根据式（6）计算w。以探测点所在海面位置处为原点，向目标方向以距离w确定反射点P0。

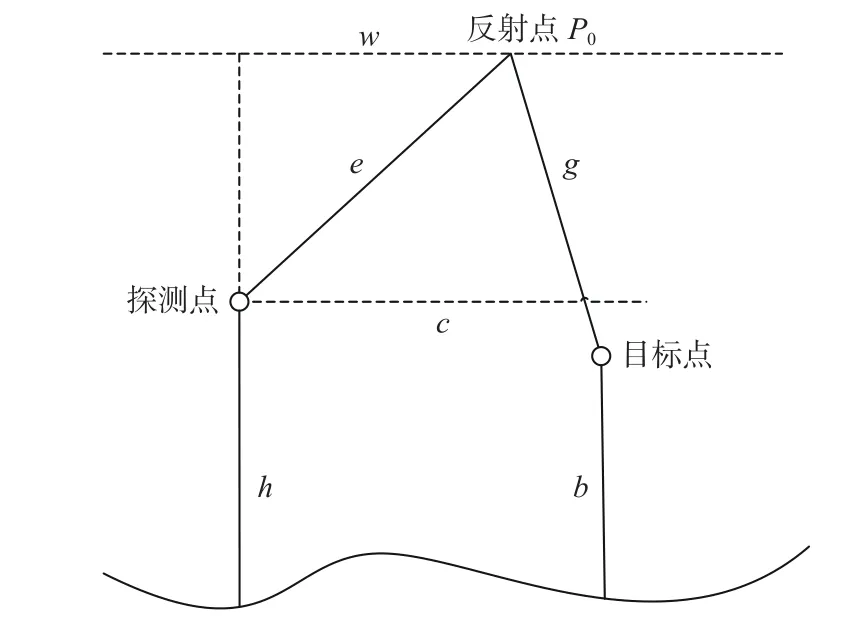
图3 水面反射探测Fig.3 Water surface reflection detection

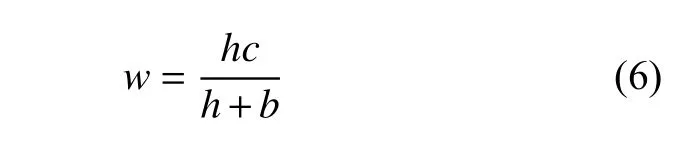
计算探测点经反射点到目标点的直线累加距离Dh：

式中：e为反射点与探测点的直线距离；g为反射点与目标点的直线距离。

若修正系数f小于1，则由式（8）对RC进 行修正：

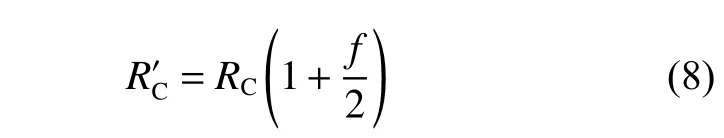
比较修正后的探测距离R′C与 反射直线累加距离Dh。若Dh＜R′C，则表明经水面反射有可能探测到目标；若Dh＞R′C，则判断为水面反射不可探测。

2.3 红方反潜机MDP建模

针对仿真推演想定中的红方作战单元进行深度强化学习训练，使红方反潜机在与环境反复交互中学会自主决策，最终自动摧毁蓝方潜艇。采用五元组 (S,A,Pa,J,γ)表示MDP，其中，S为实时获取的红方反潜机状态空间，A为红方反潜机的动作决策空间，Pa(s′,s)为红方反潜机在状态s和动作a下 进入下一个状态s′的概率，J为红方反潜机的优化目标，折扣因子 γ∈(0,1)。

1） 状态空间设置。

红方反潜机返回的态势数据约有一百多个维度，为了确保模型收敛，选择了影响任务成败的关键因素（例如经、纬度和航向）作为状态信息要素，亦即S=[经度，纬度，航向]。如图4所示，利用经、纬度坐标信息表示反潜机当前的位置，航向β表示红方反潜机当前的飞行方向与蓝方目标潜艇的偏差角度，vx和vy分别表示反潜机在x和y方向的速度。

图4 红方反潜直升机状态分析Fig.4 State analysis of red team's ASW helicopter

2） 动作空间设置。

红方反潜机可以执行的动作也有几十种，动作空间选择最能够影响任务成败的动作。例如，反潜机的航向以及是否投放声呐探测潜艇，亦即A=[航向，是否投放声呐]。

3） 优化目标设置。

如式（9）所示[8]，红方反潜机的优化目标J是同时最大化回报函数r和策略的期望熵H。式中：T为视界长度；α为温度参数，它决定了熵项对回报的相对重要性，从而控制了最优策略的随机性[11]。与传统的优化累积回报值相比，增加H项将鼓励红方进行更广泛的探索，放弃无法获得最终胜利的规划路径，与此同时，还将显著提高红方反潜机的学习速度。

回报函数r设置如下：红方靠近目标区域（以经纬度坐标（34°17'55" E，43°48'74" N）为圆心，半径为5 km的范围）会获得正回报，偏离目标区域则获得负回报，偏离目标越近或越远获得的回报绝对值越大。具体计算如式（10）所示，其中η表示反潜机目标朝向与当前朝向的绝对偏差。

当红方反潜机与蓝方潜艇间距离小于目标区域半径（5 km）时红方反潜机投放声呐。若在当前态势中红方捕获的蓝方标识符（GUID）与目标潜艇相同，则判定红方反潜机发现了蓝方潜艇。为缓解强化学习中的稀疏奖励问题，红方反潜机投放声呐和发现潜艇都将会获得10分的回报值。

推演系统的输入是神经网络推算的作战单元动作列表，依此判断红蓝双方作战单元是否被击落。若未被击落（即状态量非全为0）且执行的动作存在，则该作战单元的动作将会被执行；若红方反潜机被消灭，将获得 −100分回报值，而击毁蓝方潜艇会获得150分回报值。

3 基于SAC的决策模型构建

3.1 红方决策网络构建

在经典AC体系的基础上增加价值网络，构建红方反潜智能体的决策网络。如图5所示，其主要包括价值网络、策略网络和软Q网络这3个部分，分别引入参数化状态价值函数Vψ(st)、策略πϕ(at|st)以 及软Q函数Qθ(st,at)进行描述。3个网络单元分别具有相同结构和参数的目标网络以及在线网络，利用经验缓存数据 (st,at,rt,st+1)对目标网络进行离线策略训练，通过计算损失函数L并求解梯度（价值网络梯度 ∇ψJV(ψ)、策略网络梯度∇ϕJπ(ϕ)、 软Q网络梯度 ∇θJQ(θ)），循环更新在线网络参数，不仅可以降低样本之间的相关性，而且针对仿真推演此类大规模连续域问题，还可有效提高数据利用率。同时，对目标网络参数进行软更新，可稳定整个训练过程[12]。

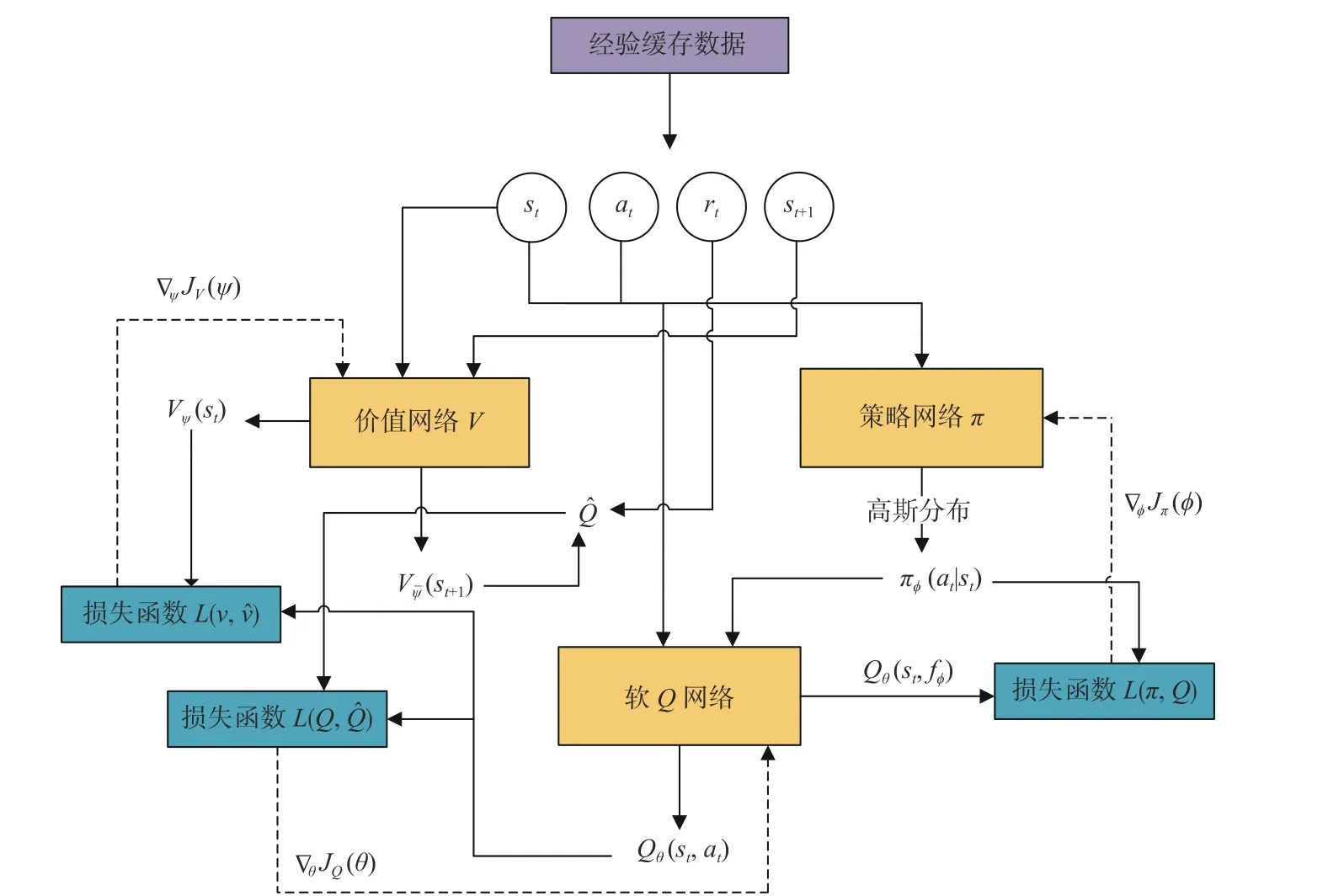
图5 基于SAC的红方直升机决策网络Fig.5 Decision-making network of red team's helicopter based on SAC

引入独立的价值网络可以使红方反潜智能体的训练更加稳定且易于与其他网络同步训练。将式（9）中的熵值项H按照期望的形式展开，将其作为价值网络更新的目标之一，得到式（11）所示的状态价值函数。如图6所示，价值网络共有4层，前3层为隐藏层，隐藏单元个数均为256；神经网络的最后一层是单维度的输出层，输出相应的状态价值V。隐藏层神经元使用Relu激活函数，以提升价值网络的非线性建模能力。

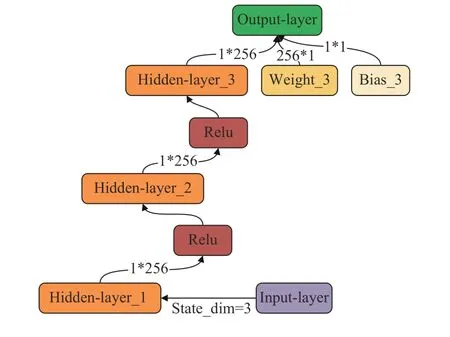
图6 价值网络结构Fig.6 The structure of value network

如图7所示，策略网络共有5层，前3层为隐藏层，隐藏单元个数分别为256，128，64；第4层神经网络对前一层的输出信息进行标准化处理，输出包含均值和标准差的高斯分布；策略网络的最后一层是2维度的输出层，根据输入状态输出相应的动作。策略网络生成的策略经高斯分布输出后（即 πϕ(at|st)），将为不同动作分配不同的概率值，这有利于红方智能体探索，提高长期回报；策略网络参数ϕ可直接通过最小化KL散度进行更新，如式（12）所示。通过重参数化，得到红方智能体要执行的随机动作，并获得新的软Q函数值Qθ(st,fϕ)，保证目标函数可微及可进行梯度更新。

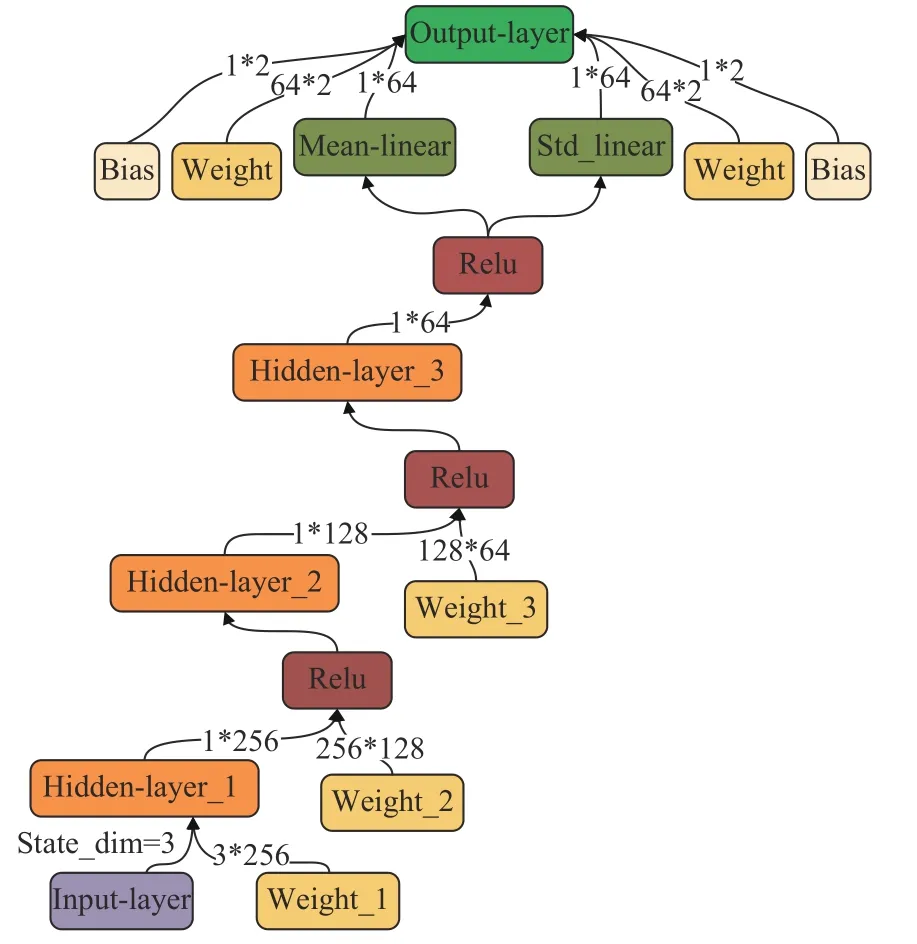
图7 策略网络结构Fig.7 The structure of policy network

式中：Zθ(st)为配分函数，使分布标准化；DKL为KL距离；fϕ(εt;st)为经神经网络变换后的重参数化策略。

将式（13）的动作函数代入式（12），策略网络的目标表达式可写为

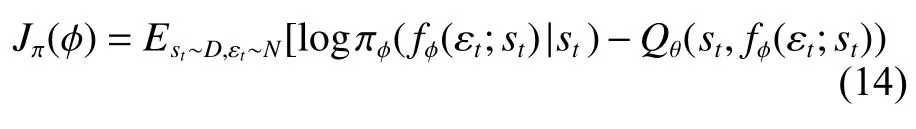
式中：E表示期望函数；εt为输入的噪声；N表示噪声呈高斯分布。

软Q网络交替进行策略评估和策略改进环节，使红方智能体获得更优策略，增强决策水平。在策略评估步骤，根据式（9）中的最大熵目标计算智能体采用当前策略π的价值。对于固定策略，可以从任何函数Q:S×A→R开始（R表示回报集），利用修正贝尔曼辅助算子Tπ[13]及根据软贝尔曼方程[14]，迭代计算动作价值函数Q，如式（15）所示。在动作集A有界的情况下，迭代次数k→∞时 ，序列Qk将收敛到Qπ。

式中，p为状态转移概率。

策略改进步骤中，策略集Π 中策略π′朝与新Q函数的指数分布呈正比的方向离线更新。首先，每个状态根据式（16）更新红方智能体策略，以保证新策略优于旧策略，即Qπnew(st,at)≥Qπold(st,at)。然后，以最小化KL散度形式减小2个分布间的差异，其中Zπold(st)为对Q值进行归一化分布。最后，经策略迭代，红方智能体找到最优策略π∗。

如图8所示，软Q网络有状态和动作2个输入维度，输入状态经过4层隐藏层，隐藏单元数分别为（256，128，256，128），输入动作经过3层隐藏层，隐藏单元数分别为（128，256，128）。进入第3层隐藏层前，将输入状态和动作2个分支的输出结果合并，经过最后单维度的输出层，输出动作状态价值Q。

图8 Soft Q网络结构Fig.8 The structure of soft Q network

3.2 红方智能体探索与利用的平衡

若红方智能体单纯执行当前策略选择回报值最大的动作，则会因探索不充分而陷入局部最优困境。为了尽快发现蓝方目标以及提高长期回报，在红方智能体训练过程中，要扩大对动作状态空间的探索。鉴于OU随机过程（Ornstein-Uhlenbeck process）时序相关性较好，故在策略网络输出确定性动作后引入OU噪声[15]，将策略随机化，再从当前策略中对动作值进行采样，得到探索动作at，如图9所示。

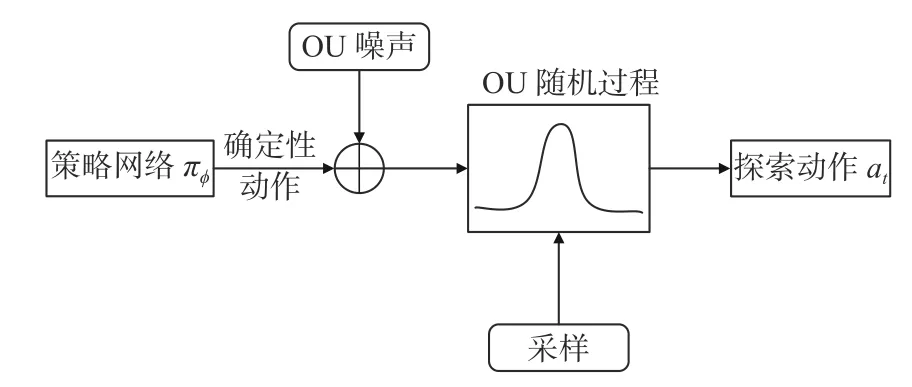
图9 红方智能体的探索动作选择Fig.9 The action choice of red team agent for exploration

3.3 算法设计

算法伪代码包括如下步骤：

步骤1：初始化价值网络参数ψ、策略网络参数ϕ以及软Q网络参数θ。

步骤3：初始化经验缓存空间D和标志位done。

步骤4：对每个episode重复执行如下操作。

1) 获取环境状态s0。

2) 若红方反潜机存在（未被蓝方潜艇摧毁或未摧毁蓝方潜艇结束推演）并且执行步数小于最大规定步数，循环执行如下操作：

(1) 将当前状态st输入策略网络，选择动作并加入OU噪声，即at∼πϕ(st)+N;

(2) 执行动作at， 获得回报rt并进入下一状态st+1；

(3) 将 (st,at,rt,st+1)存入经验缓存空间D；

(4) 若数据量大于经验回放缓存空间容量Ns，则从D中采集Ns个样本(sit,ati,rti,st+1i),i=1,2,···,Ns；

(5) 根据目标价值函数Vψ¯，计算软Q目标网络的期望回报值Qˆ：

(6) 计算价值网络的损失函数JV(ψ)，计算梯度ψJV(ψ)， 更新价值网络的所有参数ψ，其中

(7) 计算软Q网络的损失函数JQ(θ)，计算梯度θJQ(θ)， 更新软Q网络的所有参数θ，其中

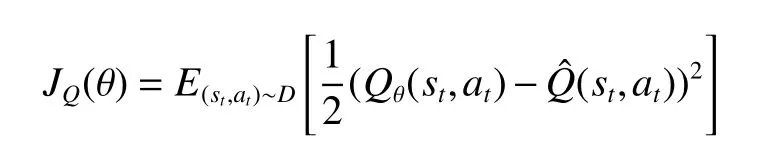
(8) 计算策略网络的损失函数Jπ(ϕ)，计算梯度ϕJπ(ϕ)， 更新策略网络的所有参数ϕ；

Qˆ(st,at)=r(st,at)+γEst+1∼p[Vψ¯(st+1)]

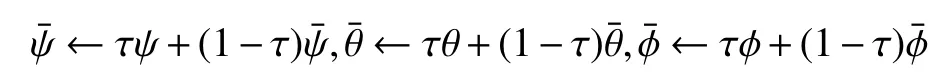
3）若蓝方潜艇被消灭（done=1）或者达到最大的规定步数，结束2)循环。

步骤5：若达到最大规定的episode数，结束整个循环。

4 作战仿真推演实验及分析

4.1 作战仿真推演环境

利用作战仿真推演平台验证决策模型的适用性，其整体框架如图10所示。作战仿真推演系统具备数据管理、指挥控制、效能评估等功能。人工智能研究平台包括Python开发包和AI处理模块两部分，与作战仿真推演系统协同配合，实现具体研究案例的智能学习。其中，人工智能研究平台的具体程序开发环境和相关接口如图11所示，主要由AI业务界面、仿真交互接口、命令池、态势池、态势适配器、算法库、通信界面组成。利用PyTorch框架编写SAC决策算法并存储到算法库，在AI业务界面中创建智能体对象和环境对象，调用算法库中的决策算法，将仿真操作命令传递给服务端执行，实时接收通信界面返回的服务端态势信息，使反潜智能体在与环境信息的不断交互中学会自主决策。

图10 仿真推演平台总体框架图Fig.10 Overall framework of simulation platform

图11 AI开发平台总体框架图Fig.11 Overall framework of AI development platform

4.2 推演结果及分析

在4.1节介绍的仿真实验环境下开展仿真推演，验证训练的红方智能体能否作出智能决策。如图12所示，在红方反潜智能体训练开始阶段，获得的回报值相对较低，每轮回报值的波动性较大。随着迭代episode数的增加，回报值相应上升，迭代进行到600轮左右时，回报值逐渐趋于平稳。相应地，在训练初期，红方反潜机不断投放声呐，四处搜寻蓝方潜艇，随机性较强，经过不断的训练学习，其发现潜艇所用的时间逐渐减少，最终实现自主决策，找到目标后自动击毁。具体训练超参数设置如表3所示。

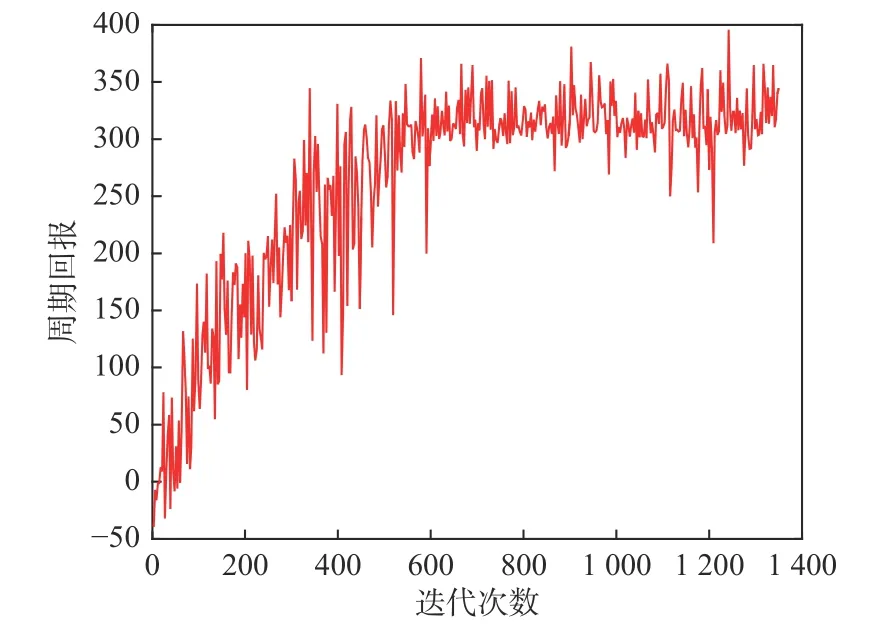
图12 红方智能体训练过程Fig.12 The training process of red team agent

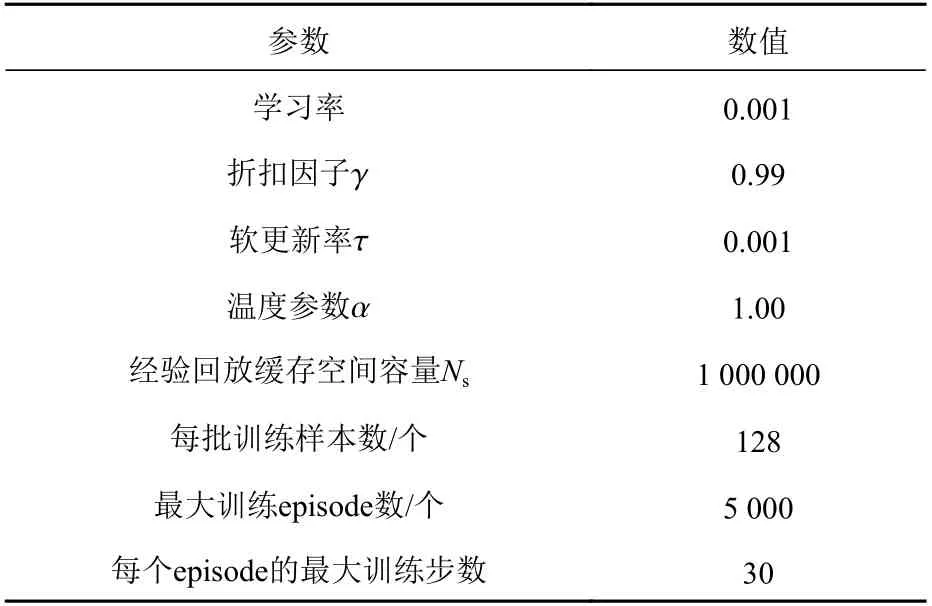
表3 超参数设置Table3 The hyper-parameter settings

图13所示为“海鹰”反潜机摧毁“鱼鳃-NN”级常规潜艇的过程。图中，左上角是“鱼鳃-NN”级常规潜艇，左下角是“阿利·伯克”级导弹驱逐舰，中间是红方反潜机为搜索蓝方潜艇而布放的声呐浮标。图14所示为对应的航迹图。图中，“海鹰”反潜机从 (34°13'E，43°48'N) 位置处出发，不断投放声呐来搜寻蓝方潜艇，最终在目标位置处 (33°85'E，43°74'N) 摧毁“鱼鳃-NN”级常规潜艇。

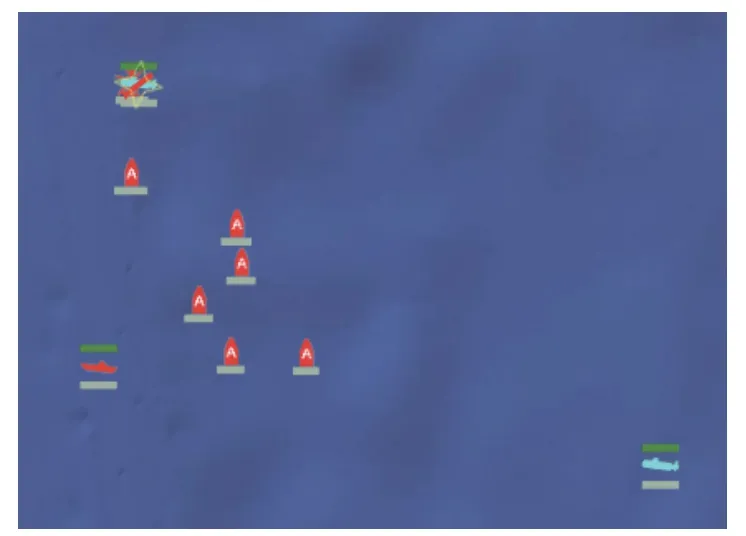
图13 红方击毁蓝方常规潜艇Fig.13 Red team destroys blue team's conventional submarines

图14 红方击毁蓝方常规潜艇航迹图Fig.14 Track map of red team destroying blue team's conventional submarine

图15所示为“海鹰”反潜机摧毁“北风之神”级战略核潜艇的过程。图中，右下角是“北风之神”级战略核潜艇级，左下角是“阿利∙伯克” 级导弹驱逐舰。图16为对应的航迹图，图中，“海鹰”反潜作战机从(34°13'E，43°48'N)位置处出发，不断投放声呐搜寻蓝方潜艇，最终在目标位置处(34°65'E，43°4'N)摧毁“北风之神”级战略核潜艇。

图15 红方击毁蓝方核潜艇Fig.15 Red team destroys blue team's nuclear submarine

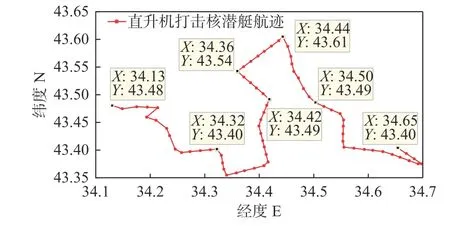
图16 红方击毁蓝方核潜艇航迹图Fig.16 Track map of red team destroying blue team's nuclear submarine

将改进SAC决策算法与DDPG决策算法对比分析，结果如图17所示。由图可见：在训练开始阶段，两种算法的平均回报均较快增长。其中，DDPG算法训练的智能体采用确定性策略作决策，经迭代300次左右开始收敛，回报值趋于稳定；而改进SAC算法采用的是探索性策略，收敛相对较慢，随着迭代次数的增加，其平均回报明显高于DDPG算法。此外，在两种算法训练的智能体性能趋于稳定后，各自随机进行了60次仿真推演实验，其中每6次实验划分为一组，共计10组实验。基于此，对10组获胜概率进行比较分析，结果如图18所示。由图可见，采用DDPG算法，红方反潜智能体的平均获胜概率为49.32%；采用改进SAC决策算法，红方平均获胜概率为73.85%，比前者提高近24.53%。

图17 两种决策算法的平均回报对比Fig.17 Comparison of average return of two decision algorithms

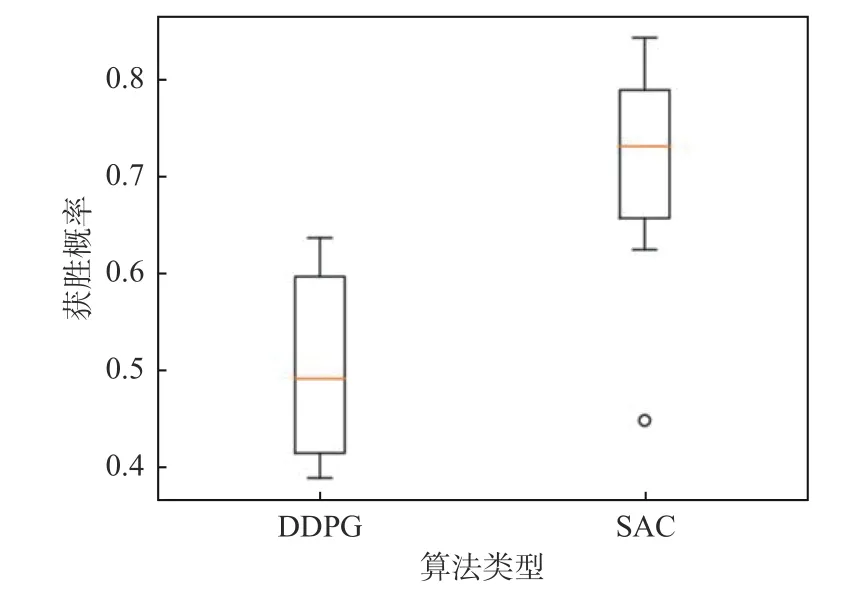
图18 红方获胜概率对比Fig.18 Comparison of winning probability of red team

5 结 语

本文针对作战仿真推演中的决策问题，提出了一种基于SAC算法的智能决策模型，使红方智能体在不具备先验知识的情况下，通过与环境不断交互，学会发现蓝方目标，自主决策，最终获得胜利。基于舰载反潜机反潜想定进行仿真推演，结果表明，本文所构建的决策模型在利用经验缓存数据开展离线策略训练后，展现出了较强的学习和判断能力，红方反潜智能体成功探测到了蓝方潜艇并进行了摧毁，从而证明了智能决策模型的有效性。在未来研究中，可以增加智能体数量，通过分析多智能体博弈特点来改进算法，以实现基于多智能体DRL的作战推演智能决策。