三相Vienna整流器中点电位自平衡离散脉宽调制策略
肖蕙蕙,陈 岚,郭 强,向文凯,苏新柱
(1.重庆理工大学 电气与电子工程学院,重庆 400054;2.重庆市能源互联网工程技术研究中心,重庆 400054)
三相Vienna整流器因开关器件数量少、电流畸变小等诸多优势备受研究者青睐[1-4],在电动汽车充电机[5]、不间断电源[6]、风力发电[7]等领域取得广泛应用,是一种极具研究价值的拓扑结构。
三电平Vienna整流器的调制策略主要有3类:载波脉宽调制(carrier-based pulse width modulation,CBPWM)[8]、空间矢量脉宽调制(space vector pulse width modulation,SVPWM)和消除特定谐波脉冲宽度调制。而七段式SVPWM以其直流电压利用率高、灵活更高等优点[9]享有举足轻重的地位。但在高频场合下,七段式SVPWM的开关损耗不容忽视,严重时甚至会引起整机效率的大幅降低。为此,相关学者对开关损耗更低的离散脉宽调制(discrete pulse width modulation,DPWM)[10-12]展开研究。任康乐等[13]针对三电平并网逆变器,从DPWM的谐波畸变、开关损耗等方面进行了详细分析。LEE等[14]提出了基于载波实现的DPWM策略,通过向参考电压中叠加改进的偏置电压,实现Vienna整流器的DPWM,其算法简单且易于实现。更进一步地,在此基础上,添加了可变功率因数分析。文献[16]中提出一种单极箝位脉宽调制方法,在解决单相三电平中点箝位逆变器高功率损耗问题的同时克服了传统DPWM 输入电流失真的弊端。
上述文献虽降低了开关损耗,但均未考虑三电平拓扑固有的中点电位平衡问题。而中点电位不平衡会造成部分开关器件受压增加、交流侧低次谐波含量上升等后果。为此,文献[17]针对三电平逆变器,提出了一种能兼顾中点电位平衡的DPWM算法,该算法通过传统DPWM1和DPWM3的冗余矢量切换来调节中点电位。文献[18]针对二极管箝位型三电平逆变器,提出了一种基于载波的虚拟空间矢量的调制策略,其通过改变某一相1电平的作用时间来实现直流侧上下电容的均压,但增加了额外的开关损耗。文献[19]针对中点箝位型逆变器,提出了一种基于电路级解耦原理的DPWM策略,该方法能实现无任何反馈控制时的中点电位平衡,但输入电流存在过零点畸变现象。文献[20]的研究中向调制波中注入不同的零序电压来调节中点电位,通过过零点钳位来降低开关损耗,但未实现损耗的最小化。
综上所述,常用的七段式SVPWM策略可通过控制正负小矢量的作用时间来平衡中点电位,但开关损耗较大。关于DPWM策略,目前大多数文献只能单方面解决开关损耗或中点电位平衡问题,将两者结合研究的文献很少且不系统。因此,本文中针对一种三相类Vienna拓扑,提出中点电位自平衡的DPWM策略。该策略采用五段式DPWM箝位某相电压并经矢量序列优化进一步减小开关损耗,通过箝位模式的切换来调节中点电位,使系统在高开关频率场合下也能确保低开关损耗和中点电位平衡,提升整流器的整体效率与可靠性。
1 三相Vienna整流器及其矢量空间
图1为三相三电平类Vienna主电路拓扑。其中,Vga、Vgb、Vgc为三相电网电压;L为升压滤波电感;R为电网线路的等效电阻;ia、ib、ic为三相输入电流;C1、C2为稳压滤波电容;Rload为阻性负载。

图1 三相三电平类Vienna主拓扑示意图
由图1可知,三相Vienna整流器A、B、C三相桥臂结构一致,均由4个二极管和2个功率开关管Sj1、Sj2构成。其中Sj1与Sj2状态互补。根据图1整流器拓扑的工作原理,定义开关函数为:
(1)
其中:j表示a、b、c;Sj表示j相的开关状态。
在式(1)开关函数的基础上,建立Vienna整流器等效开关模型,如图2所示。

图2 Vienna等效开关模型示意图
若Sj=2,桥臂电压被钳位至P电平(+Udc/2电平);若Sj=1,桥臂电压被钳位至O电平(0电平);若Sj=0,桥臂电压被钳位至N电平(-Udc/2电平)。由此可知,整流器每相桥臂的2、1、0这3种开关状态均存在电位状态与之对应,三相可产生33=27种状态组合,但受限于输入电流的极性,三相Vienna整流器中(222)和(000)状态不存在。故采用25个电位状态作为基本矢量形成矢量空间;以6个大扇区(Ⅰ-Ⅵ),6×6=36个小扇区(D1-D6)的方式进行分区。结果如图3所示。由图3可见,从幅值的角度看,整个矢量空间由4种元素构成,即6个大矢量、6个中矢量、12个小矢量(正、负小矢量)和1个零矢量。一般利用小矢量相应的2种冗余开关状态中点电位作用相反的特性来调节中点电位。
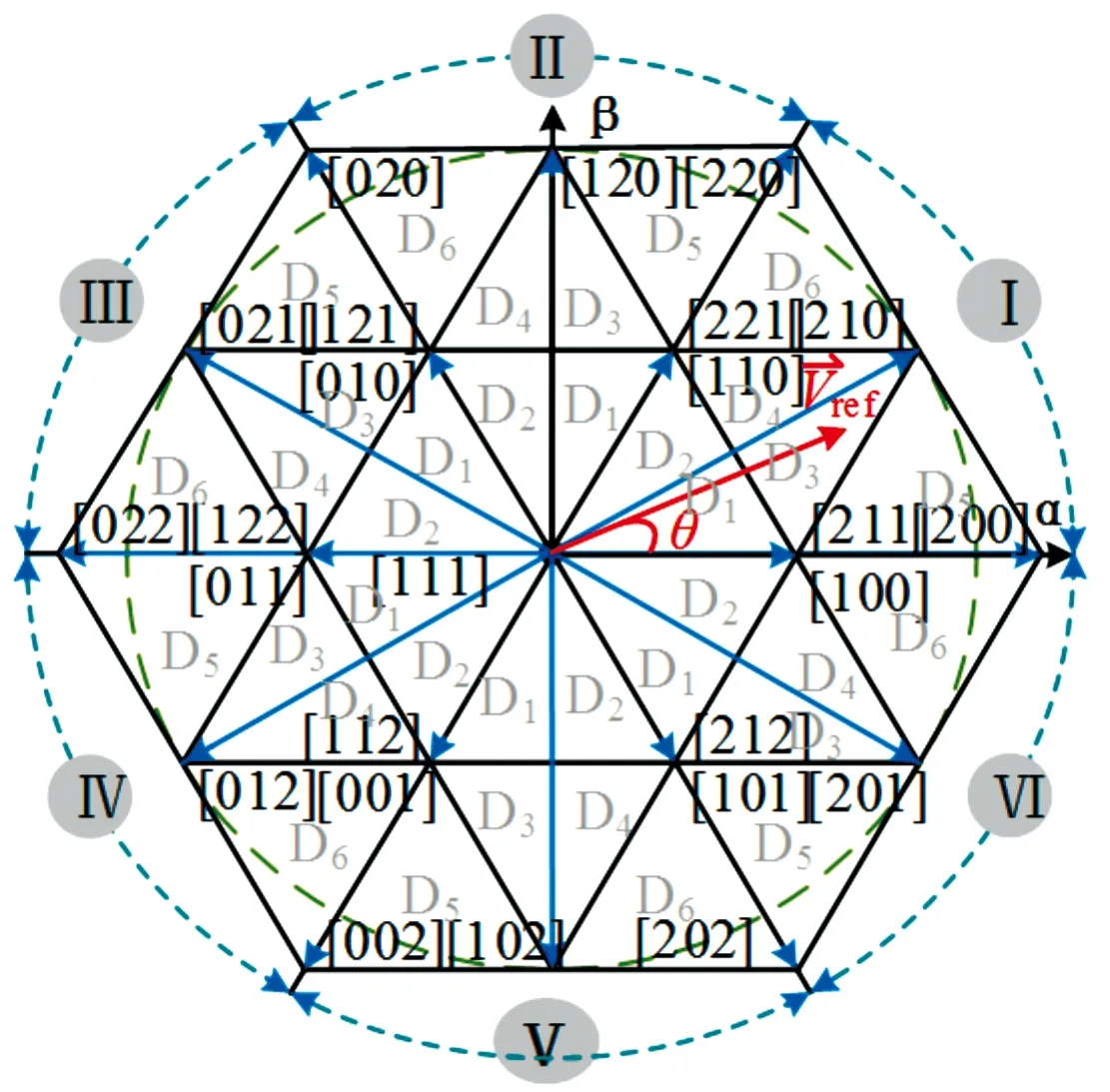
图3 三相Vienna整流器的矢量空间示意图
2 Vienna整流器的中点电位自平衡的离散脉宽调制策略分析
2.1 冗余箝位模式及其矢量序列
本文中所提中点电位自平衡DPWM策略的核心是2种冗余箝位模式。下面以大扇区Ⅰ中小扇区D3、D4为例,详细说明箝位模式及其矢量序列的确定过程。当参考矢量Vref位于扇区D3或D4时,矢量分布如图4所示。

图4 Vref位于扇区D3或D4的矢量分布图
步骤1 根据参考矢量Vref所处扇区的输入电压极性,判断其最近三矢量是否存在不可用的冗余小矢量。若存在,采取排除措施改善电流畸变现象。
扇区D3所处位置有Vgb﹤0,而使用正小矢量(221)的前提条件与之相反,为保证Vienna整流器的电网电压与输入电流同相运行,故标记为不可用矢量,不再使用。扇区D4有Vgb﹥0,使用负小矢量(100)的条件与之违背,也不可用。同理,判断其余小扇区不可用小矢量的存在情况,整理后结果如表1所示。
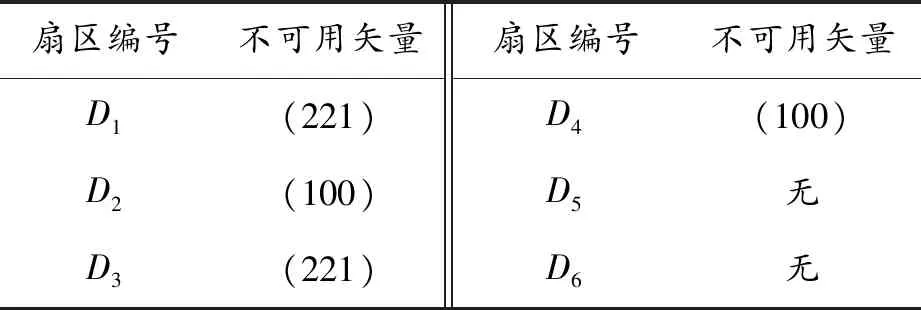
表1 大扇区I中不可用矢量存在情况
步骤2 排除小扇区中不可用小矢量后,根据最近三矢量原则,一个开关周期中,在保持某相开关状态不变、每次只动作一相开关、开关状态对称分布的前提下,利用各扇区的可用基本矢量形成相应的DPWM矢量序列,初步得到各个小扇区对应的2种箝位模式。扇区D3、D4的箝位模式如图5和图6所示。
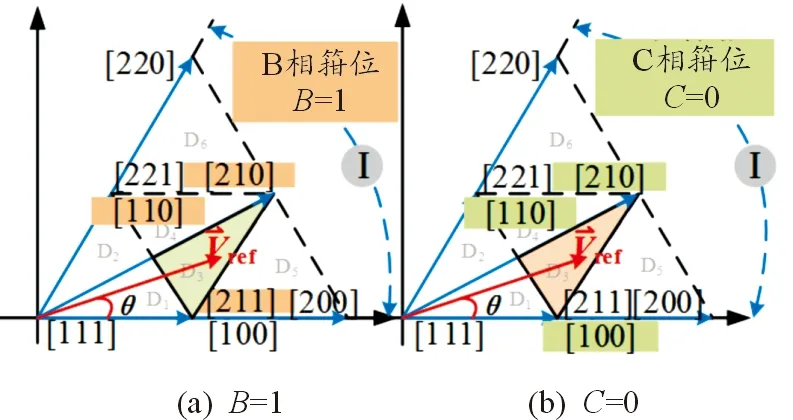
图5 小扇区D3的冗余箝位模式

图6 小扇区D4的冗余箝位模式
步骤3 为实现扇区切换时开关次数的最小化,进一步优化矢量序列。在扇区D3、D4的B=1模式中,利用零矢量(111)分别替换矢量(110)与矢量(211)后,可得优化后的最终矢量序列。
表2给出了大扇区Ⅰ中各个小扇区的箝位模式以及对应的矢量序列。其中,扇区D5、D6只需前2个步骤即可确定矢量序列。

表2 大扇区I的矢量序列
2.2 计算基本矢量作用时间
确定矢量作用序列后,可通过式(2)计算各个基本矢量对应的作用时间。
(2)
其中:V1、V2、V3为合成参考矢量Vref的基本矢量,带下标α、β的量表示对应矢量在α、β轴上的投影。
利用中矢量幅值作为系数进行归一化处理,再求解式(2)可得到大扇区Ⅰ的各小扇区中基本矢量的作用时间,如表3所示。
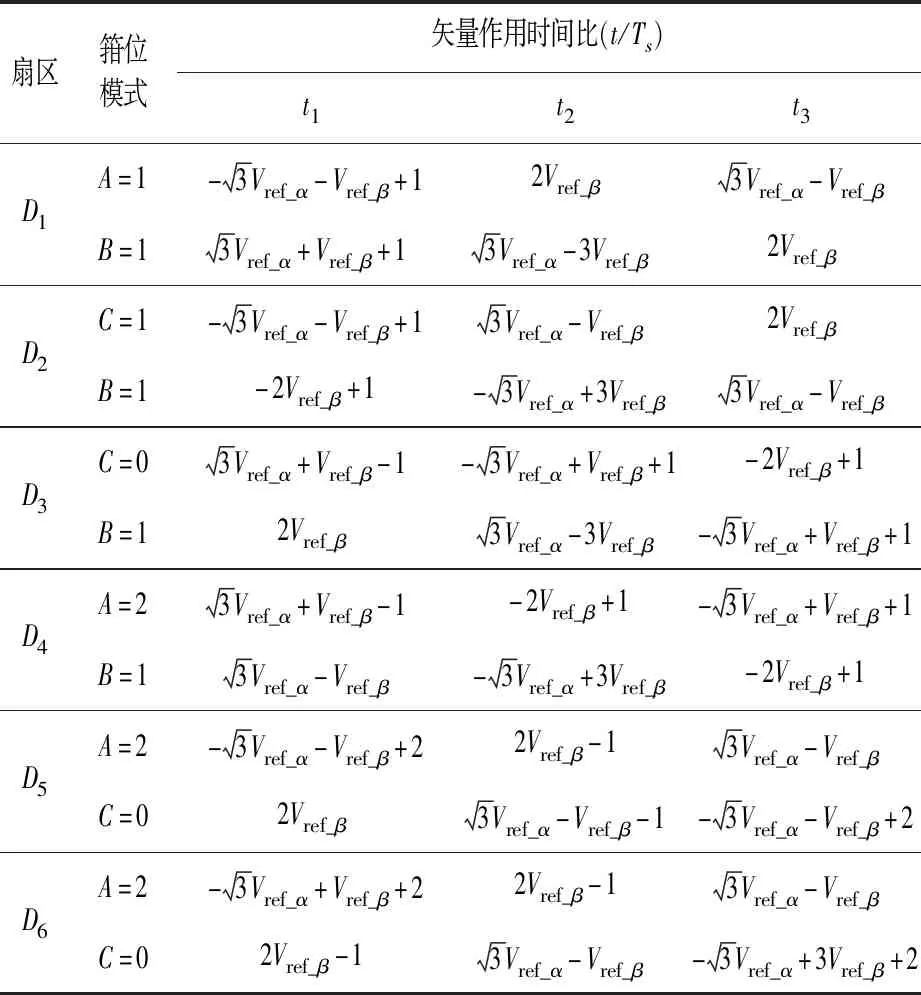
表3 大扇区Ⅰ的矢量作用时间比
当参考矢量位于其他大扇区时,可将所在扇区的全部矢量等效转换到大扇区Ⅰ。故表3的计算式适用于所有大扇区。
3 中点电位分析及其控制策略
3.1 中点电位分析
利用所提冗余箝位模式的切换可解决DPWM的中点电位平衡问题。图7是整流器直流侧电路的局部图。由图7可知,中点电位波动情况取决于流入中点o的电荷量,进而与中点电流io有关。
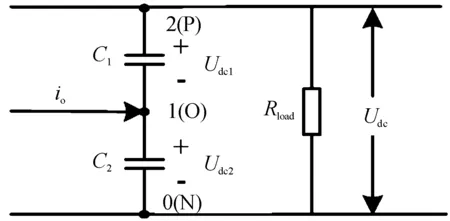
图7 Vienna整流器直流侧电路局部图
以大扇区Ⅰ中小扇区D5为例,详细分析A=2、C=0这2种矢量序列对中点电位的影响,并给出调节中点电位的方法。根据表2中小扇区D5的2种矢量序列,结合图7,可得序列中各个基本矢量所产生的中点电流io。小扇区D5中各基本矢量所产生的中点电流如表4所示。

表4 小扇区D5中各基本矢量所产生的中点电流
进而可得采用A=2、C=0箝位模式时流入中点的瞬时电荷量QA、QC的表达式为:
(3)
其中:t1、t2、t3为表3中对应的基本矢量作用时间,此处设置上标“*”以区分A=2、C=0这2种模式。
由表3可知,此时:
(4)
定义调制比m为:
(5)
其中|Vref|为参考矢量幅值。
系统处于稳态时,有:
(6)
将式(5)(6)代入式(3)中,得到QA、QC关于幅角θ的表达式,经整理得:
(7)
系统处于单位功率因数运行时,在大扇区Ⅰ中有:
(8)
其中Im为三相电流的幅值。
将式(8)代入式(7)中,经整理得到:
(9)
其中:
(10)
采用式(9),根据调制比m=0.78、fs=20 kHz绘图。结果如图8、9所示。
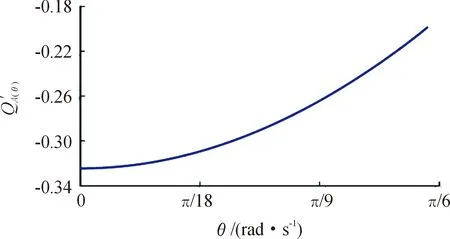
图与θ的关系图


图与θ的关系图
3.2 中点电位平衡算法
综上分析,通过各个扇区内2种箝位模式的切换,可实现对中点电位的调节。下面给出本文中点电位平衡算法的控制流程,如图10所示。
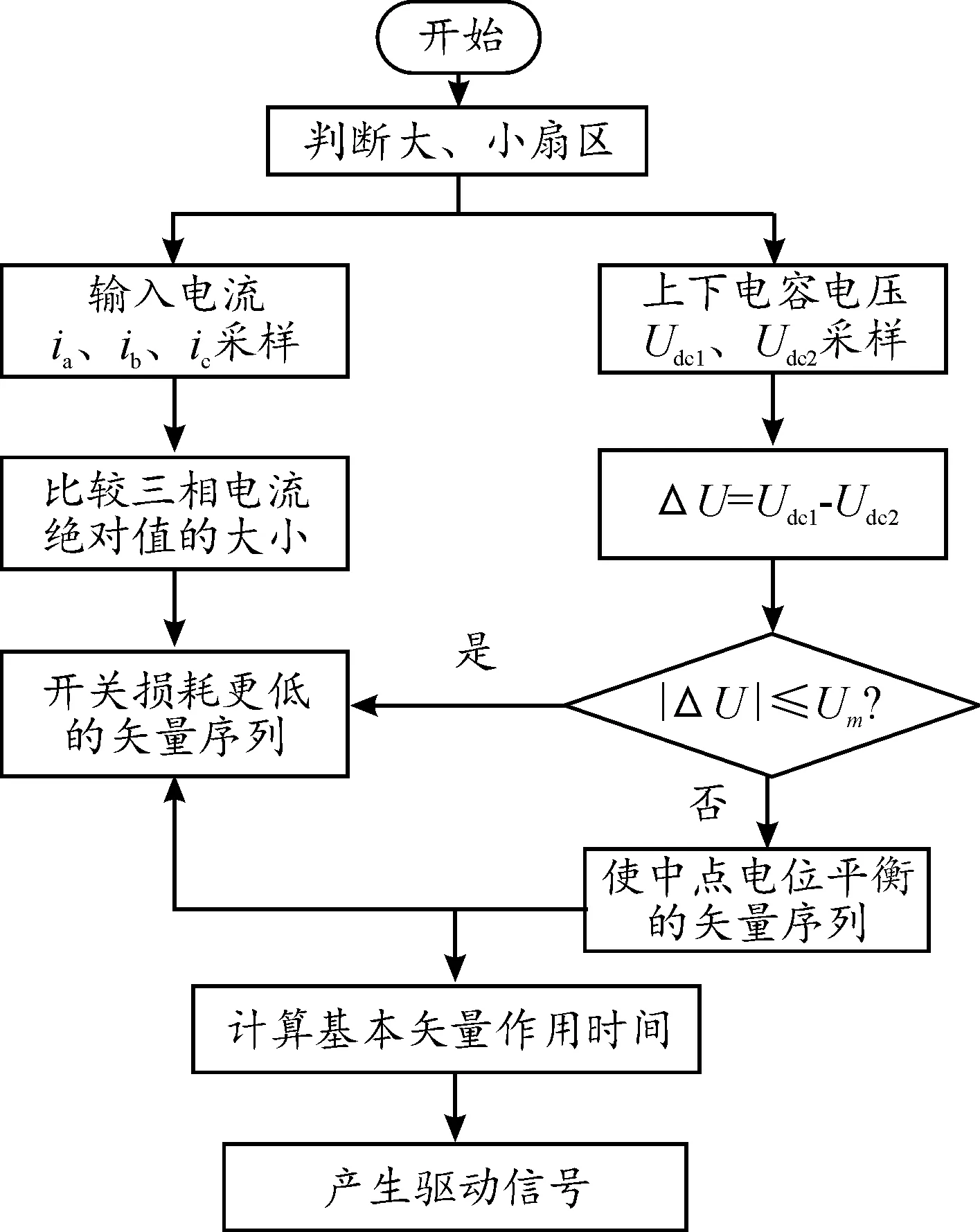
图10 中点电位平衡控制流程框图
本文中所提的中点电位自平衡DPWM策略兼顾低开关损耗和中点电位平衡,因此必然允许中点电位存在微量正常范围内的波动。该策略流程如下:首先,根据参考矢量所在位置,通过采集直流侧上下电容电压Udc1、Udc2,计算压差ΔU=Udc1-Udc2;由于采用箝位电流绝对值更大的相时,降低开关损耗的能力更强,故通过采集三相输入电流ia、ib、ic的信息以判断2种箝位相中电流绝对值较大的相,进而确定开关损耗更低的矢量序列。例如,在小扇区D1中有|ia|>|ic|>|ib|,经对比,表2中A=1、B=1这2种序列,开关损耗更低的是A=1模式;其次,设定恰当的阈值±Um,判断压差ΔU所处的区间。若处于设定的阈值范围内,则选择开关损耗更小的箝位模式。若ΔU>Um,则选择使中点电位上升的箝位模式,若ΔU<-Um则选择使中点电位下降的箝位模式;最后,根据选择的矢量序列计算各基本矢量的作用时间(表3),产生脉冲信号以驱动开关管。
4 仿真及实验结果分析
为验证所提中点电位自平衡DPWM策略的正确性,用Matlab/Simulink建立仿真模型,并搭建实验样机。Vienna整流器参数如表5所示。

表5 Vienna整流器参数
图11为三相Vienna整流器实验样机,由主拓扑、电流电压传感器、主控芯片、信号调理电路、滤波单元、供电电源及驱动电路等构成。
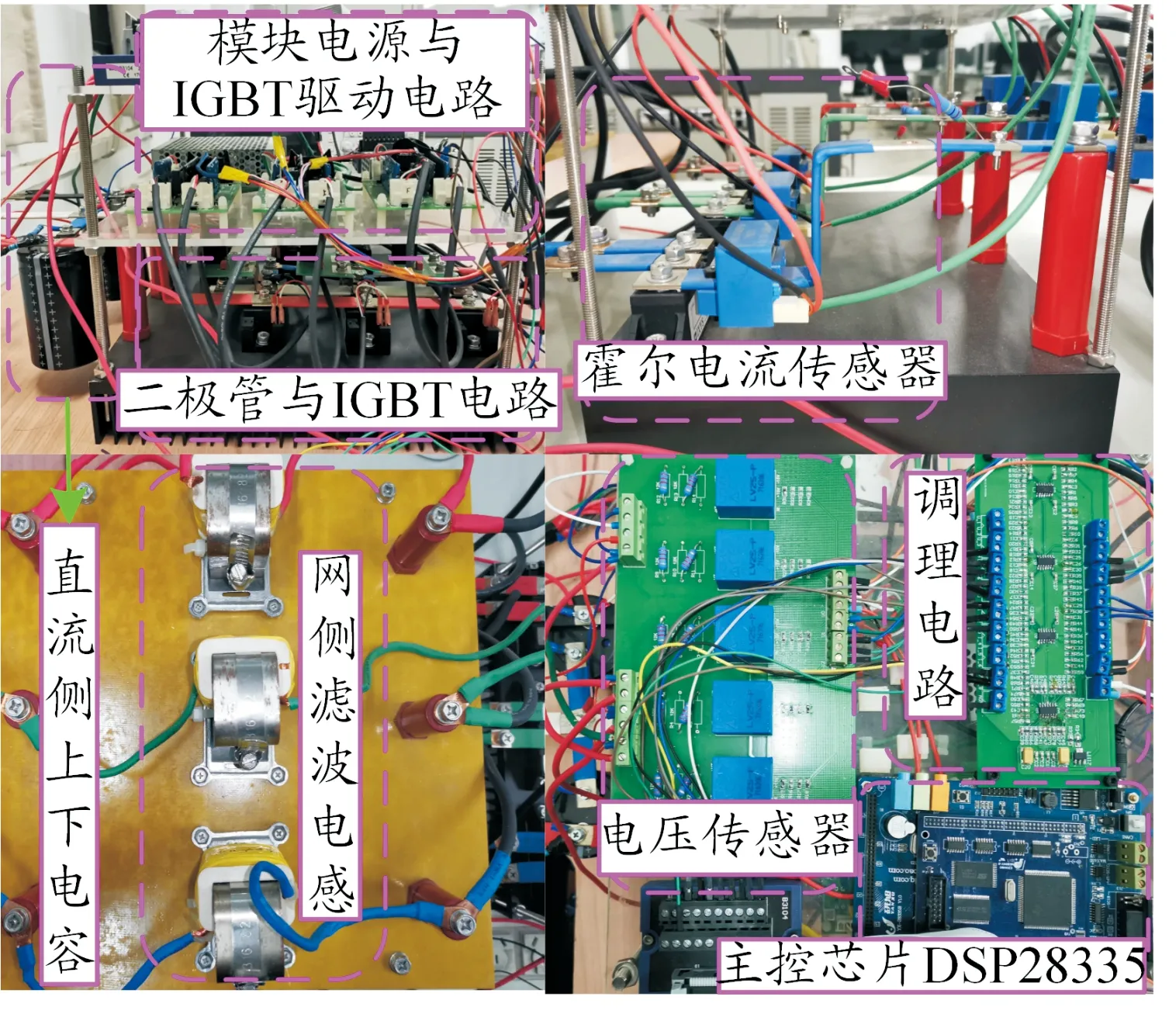
图11 Vienna整流器实验样机布置图
4.1 仿真结果分析
在Matlab/Simulink中建立仿真模型,设定系统仿真总时长t=1.5 s;运行至0.5 s时,负载Rload功率由10 kW突变为5 kW;运行至1 s时,由5 kW突变为10 kW。
图12为整个仿真过程中直流侧上下电容电压Udc1、Udc2的波形。由图12可见,在系统处于满载和半载稳定运行时,直流侧上下电容实现均压,均能控制在350 V附近(直流侧输出电压Udc为给定值700 V的一半),且静差较小。当负载由满载(10 kW)切换至半载(5 kW)时,其超调量约为2.8%,调节时间为59.2 ms;当负载由半载(5 kW)切换至满载(10 kW)时,电压跌落量约为2.5%,调节时间为76.8 ms。负载突变时能快速、准确地跟踪参考值,动态特性良好。

图12 直流侧电容电压波形
图13为整个仿真过程中直流侧上下电容压差ΔU的波形。由图13可见,ΔU被限制在本文设定阈值±Um=±2.5 V范围内,中点电位波动较小,输出特性良好。
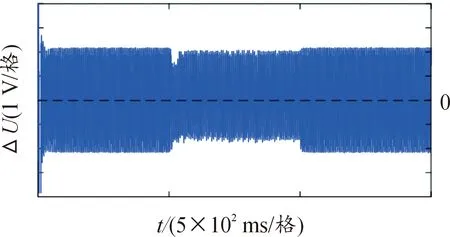
图13 直流侧上下电容压差波形
图14为正半周期内A相上管Sa1的开关指令波形。由图14可见,调制过程中开关管存在一定的不动作区间,有效减少了开关动作次数,降低了开关损耗。
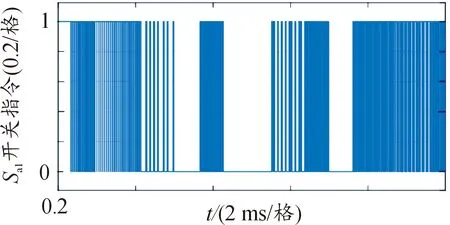
图14 正半周期内A相上管Sa1开关指令
图15为系统额定功率运行、负载在满载与半载之间来回切换3个阶段中A相电网电压Vga与输入电流ia的波形。由图15可见,整个过程中电网电压与输入电流相位几乎一致,保证了单位功率因数的运行。
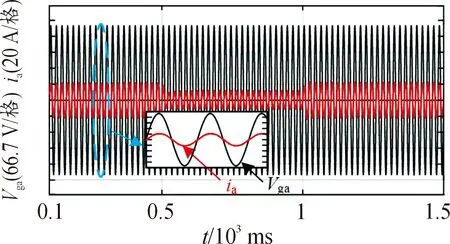
图15 A相电网电压与输入电流波形
图16为额定功率下AB线电压Vab波形。由图16可见,AB线电压为典型的五电平阶梯波,完全符合三电平整流器的特征。
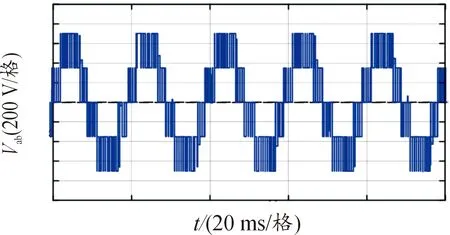
图16 额定功率下AB线电压波形
在额定功率运行时,对A相电流进行快速傅里叶变换(fast Fourier transform,FFT)分析,得到总谐波畸变率(total harmonic distortion,THD)波形,如图17所示。由图17可见,THD值约为2.30%,相对于国家谐波治理规定指标5%而言,电流畸变较小,系统输入特性良好。

图17 额定功率运行时A相电流总谐波畸变率
图18为系统额定功率运行、负载在满载与半载之间来回切换3个阶段中整流器的输入有功功率P、无功功率Q及功率因数λ的波形。由图18可见,整流器在负载突变时,瞬时有功功率能快速准确地跟踪给定值,而无功功率始终保持在零值附近,功率因数始终大于0.97,实现了功率因数校正。
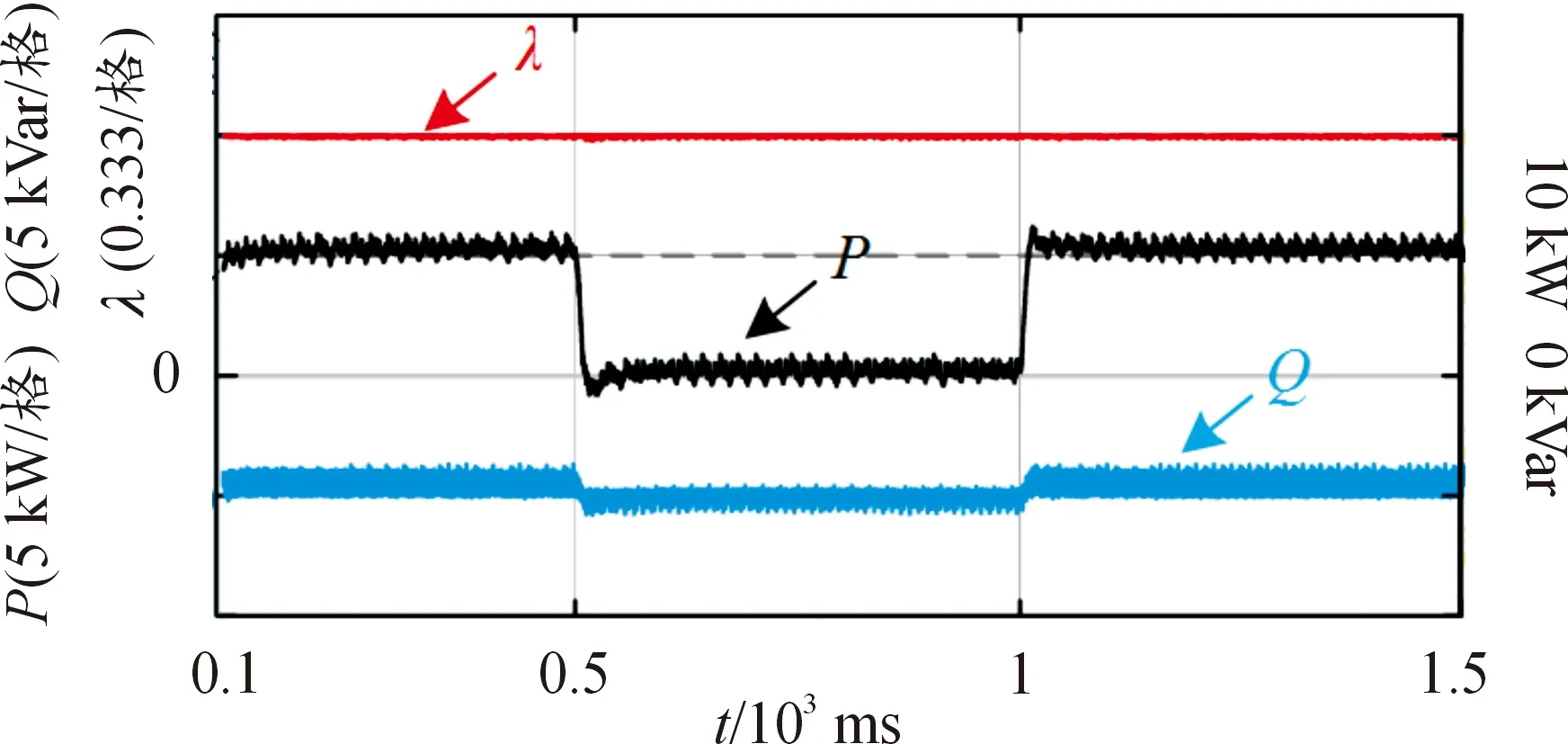
图18 有功功率、无功功率和功率因数波形
4.2 实验结果分析
搭建10 kW三相Vienna整流器样机进一步验证所提调制策略的性能。
图19为额定功率下线电压Vab的实验波形,其结果与仿真几乎一致。
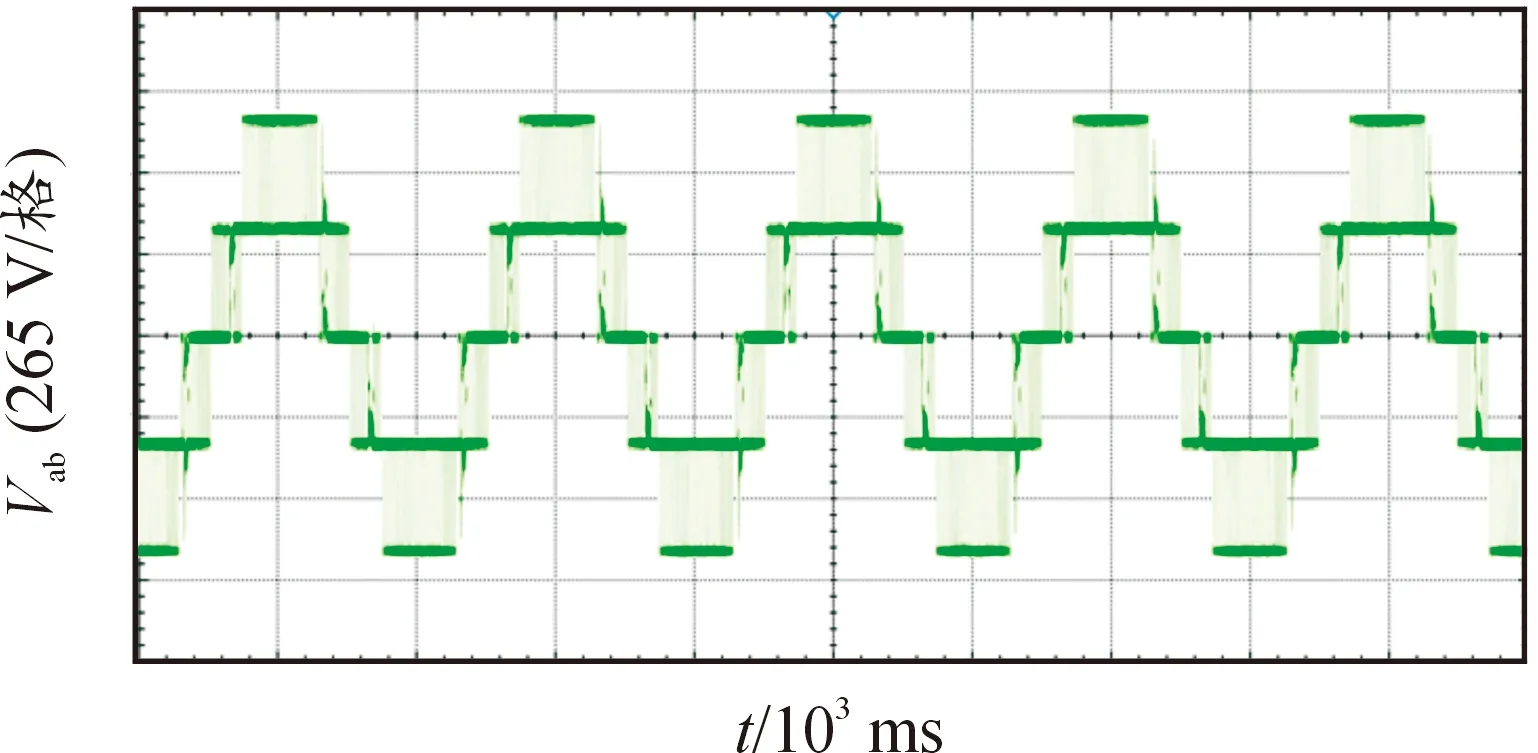
图19 额定功率下线电压实验波形
图20为负载突变时,直流侧上部电容电压Udc1、A相电网电压Vga及电流ia的实验波形。由图20可见,在不同负载的稳定运行过程中,输入电流畸变均较小;在2次负载切换时,上下电容电压均可在4个工频周期内平稳过渡至新稳态,动态调节速度较快。
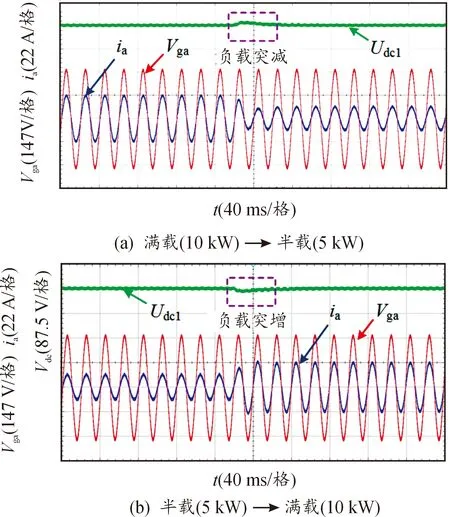
图20 动态响应实验波形
图21为上下电容压差ΔU的波形。由图21可见,系统即使处于切换负载的调节过程中,中点电位波动也较小,上下电容电压基本保持平衡,说明所提调制策略的中点电位调节能力在动态过程中也有效。

图21 上下电容压差ΔU的实验波形
将A相电流实验波形导入Matlab中,在额定负载运行段进行FFT分析可得图22。由图22可见,A相电流THD值为3.18%。鉴于实际电路中非理想因素(各个元件硬件寄生参数、线路寄生参数等)的存在,视该结果与仿真结果相一致。

图22 额定功率下A相电流THD波形
5 结论
1)与传统DPWM相比,所提出中点电位自平衡DPWM策略可控制中点电位平衡且电容电压波动小。
2)通过调制策略本身的改进降低开关损耗,在高开关频率场合更具优势。

