具有收获项的时滞捕食系统的Hopf分支

吕堂红，于智博，周林华

(长春理工大学 数学与统计学院，吉林 长春 130022)

0 引言

捕食者-食饵模型是描述两个物种之间相互作用的基本微分方程模型，已经得到研究人员的广泛关注.功能反应函数和人为的收获可以影响种群的动态.常见的功能反应函数主要有Holling I-Ⅳ型、比率型、Hassell-Varley型、Crowley-Martin型等.在生态系统中，猎物与捕食者之间的相互作用是影响群落结构和生态系统稳定性的重要因素之一.掌握捕食者和食饵之间的动态行为可以进一步理解两者之间的关系平衡生态系统.近年来生物学研究表明，食饵针对捕食者的狩猎行为，会自发的进行群体防御，即将较为弱小的同类聚集在种群内部，使捕食者的狩猎行为仅发生在种群的边界上[1].2011年，V.Ajraldi[2]首次提出具有群体效应的捕食者-食饵模型，即用带有食饵平方根的功能型反应函数来描述具有这种群体效应的捕食系统的动力学行为.H.Jiang和H.Fang[3]提出并研究了具有群体效应和Smith增长的捕食者-食饵模型，给出了系统存在Hopf分支的充分性条件.F.Souna等[4]提出并探讨部分食饵具有群体效应的捕食系统的动力学行为，分析了系统正平衡点的存在性和稳定性.2018年，F.Zhang[5]等研究了如下形式的具有群体防御和扩散的时滞Lesile-Gower捕食系统：

(1)

事件的状态通常取决于过去的历史.时滞的引入，对于系统的刻画变得尤为重要.由于泛函微分方程相比于常微分方程，具有更加丰富的动力学性质，如周期解、极限环、Hopf分支等，已经引起学者广泛的研究.王玉杰等[6]研究了免疫细胞具有时滞效应的HIV模型的稳定性，分析了边界平衡点的局部渐近稳定性和全局渐近稳定性，对肿瘤免疫疗法提供了一定的借鉴.为提高对捕食者-猎物模型动态的理解，一个更现实的方法是，将生物具有的成熟时间、捕获时间、消化时间等时滞现象纳入描述生物种群动态的数学模型中.时滞的存在会导致种群数量产生波动，将原有的稳定状态变为不稳定状态，是影响捕食系统稳定性的重要因素.在研究种群动力学模型中，引入时滞是更具有实际意义的[7].

种群生态学中最重要的因素之一是收获.捕捞意味着由于狩猎或捕获个体从而对种群数量具有负面影响.因此，从生态和经济的角度来理解收获对多物种生态系统动态的影响是很重要的.X.Song等[8]已经研究了一个关于收获成熟种群的阶段结构竞争系统.研究了所提模型的最佳采收策略和稳定性.T.K.Kar和K.S.Chaudhury[9]研究了一个由两个竞争物种与捕食者相互作用组成的多物种种群收获模型.收获函数，一般可以分为线性和非线性两种类型.从生物和经济的角度来看，非线性收获函数更适合在现实中使用.在过去的几年里，带有非线性收获项的捕食者-猎物模型已经被广泛的研究[10-12].结果表明，收获对捕食者-猎物模型的动力学行为有很强的影响，会改变系统的稳定性，产生周期解、极限环等现象.因此，在捕食者-猎物模型中考虑收获是有意义的.

(2)

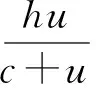
1 局部稳定性分析

令E*(u*，v*)是系统(2)的非负平衡点，则E*(u*，v*)满足：

因此有u*=v*，且u*满足：

A0t4+A1t3+A2t2+A3t+A4=0.

其中：

由Descartes符号法则易知当满足

(H1)：h-αc<0

时，系统(2)至少存在一个正平衡点E*(u*，v*).系统(2)在E*处的Jacobi矩阵为

其中：

则在E*处的特征方程为

λ2+Aλ+Be-λτ+C=0.

(3)

其中：

当τ=0时，系统(2)的特征方程(3)变为

λ2+Aλ+B+C=0.

根据Routh-Hurwitz准则，若

(H2)：A>0，B+C>0，

系统(2)的正平衡点E*是局部渐近稳定的.

当τ>0时，系统(2)的特征方程(3)变为

λ2+Aλ+Be-λτ+C=0.

(4)

令λ=iω1(ω1>0)是该方程的根，代入到式(4)有

(5)

两边分别平方相加可得

(6)

引理1当C2-B2<0，τ=τk时，方程(5)有一对纯虚根λ=±iω1(ω1>0).其中：

(7)

下面验证横截性条件.对于(4)式关于τ求导有

(8)

经计算有

(9)

假设

因为

所以

于是有如下结论.

2 局部Hopf分支方向及其稳定性

由已知结论可以得到，在平衡点的附近，局部Hopf分支是存在的.下面研究在τ=τ0条件下，运用文献[13]给出的研究Hopf分支的方法，得到在E*(u*，v*)处有关Hopf分支的计算表达式.

(10)

(11)

F(μ，φ)=(τ0+μ)(F1(μ，φ)，F2(μ，φ))T.

(12)

其中：

由泛函分析有关定理，存在一个有界变差的二阶矩阵

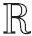
使得

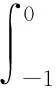
(13)

其中

δ(θ)是Dirac-delta函数.

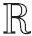
和

于是，系统(10)变为

(14)

其中u=(u1，u2)，ut(θ)=u(t+θ)，θ∈[-1，0].

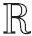
和

设A和A*对应于特征根iω0τ0与-iω0τ0的特征向量分别为q(θ)和q*(s).

A(0)q(θ)=iω0τ0q(θ)，A*(0)q*(s)=-iω0τ0q*(s).

可得：

其中：

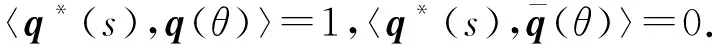
下面计算在μ=0处的中心流型C0令Xt处为μ=0时方程为(14)的解.定义

(15)

在中心流型C0上，有

(16)

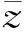
(17)

再由式(16)—(17)得

Xt(θ)=W(t，θ)+2Re{z(t)q(θ)}，

综合式(12)得

通过比较系数可得：

为了确定g21下面计算W20(θ)和W11(θ)由式(14)和(15)得到：

即

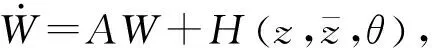
(18)

其中

(19)

结合式(15)—(16)得到

其中

(20)

通过比较系数得到

(2iω0-A)W20(θ)=H20(θ)，-AW11(θ)=H11(θ).

由式(18)可知，当θ∈[-1，0)时，

(21)

比较式(20)—(21)有

W20(θ)，W11(θ)的计算结果如下：

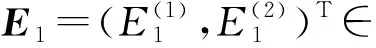
这就意味着，可以得到

(22)

(23)

其中，C1(0)由式(22)给出，易得出μ2，β2，T2的值.因此有定理2成立.

定理2当τ=τ0时，由式(23)的各个表达式得出下面的结论：

(1)μ2确定Hopf分支的方向.如果μ2>0(μ2<0)，则Hopf分支是超临界的(次临界的)；

(2)β2决定Hopf分支的稳定性.如果β2<0(β2>0)，则Hopf分支是稳定的；反之，是不稳定的；

(3)T2决定Hopf分支的周期.如果T2>0(T2<0)，则Hopf分支周期解的周期增加；反之是减少的.

3 数值模拟

为验证上述结论，考虑如下模型：

(24)

满足定理1，系统(24)有唯一平衡点

E*(u*，v*)=E*(0.363 1，0.363 1).

当τ>0时，条件(H1)和(H3)满足，通过计算有

ω0=0.389 2，τ0=2.633 2，C1(0)=-86.188 1-93.355 2i，

μ2=-75.610 2，β2=-172，T2=1.690 2.

由定理2可知，系统(24)的Hopf分支是次临界的，分支周期解是稳定的且分支周期减小.横截性条件满足.因此当τ=2.625<τ0=2.633 2时，平衡点E*是渐近稳定的，见图1；当τ=3.35>τ0=2.633 2时，平衡点E*失去稳定性，见图2.

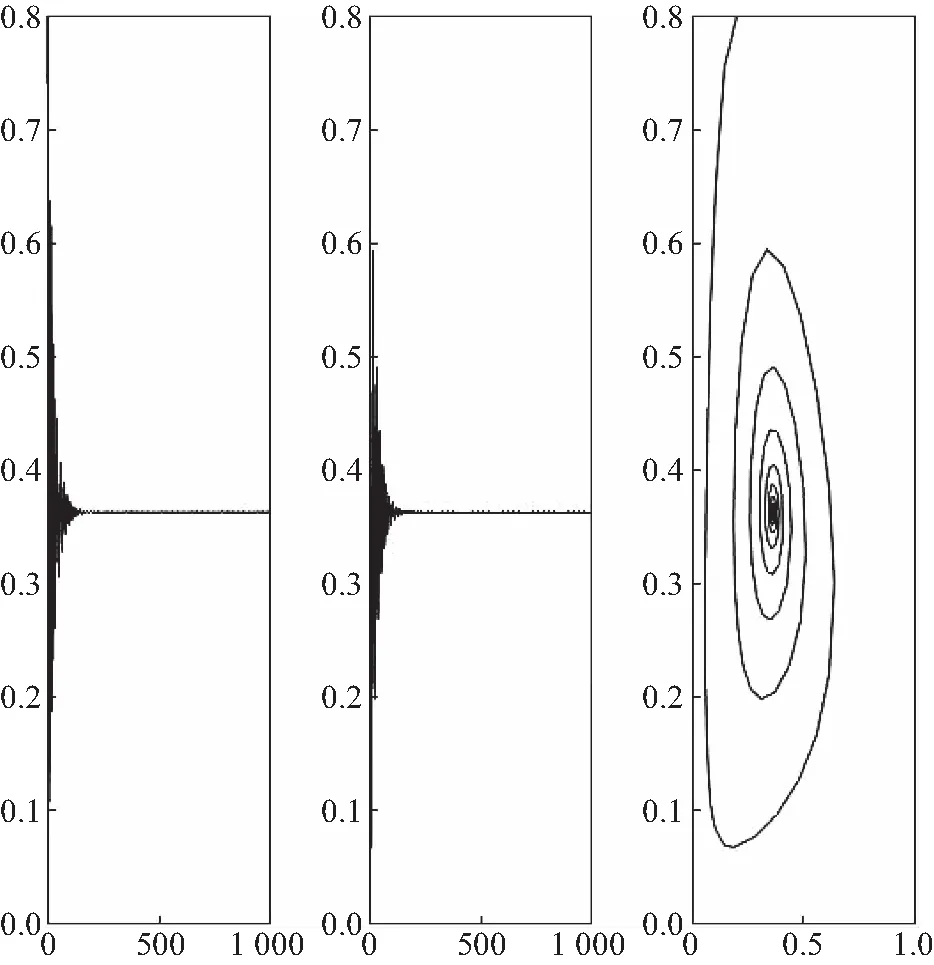
图1 当τ=2.625<τ0=2.633 2时，系统(24)的平衡点和相图Fig.1 Equilibrium and phase orbit of system (24) when τ=2.625<τ0=2.633 2

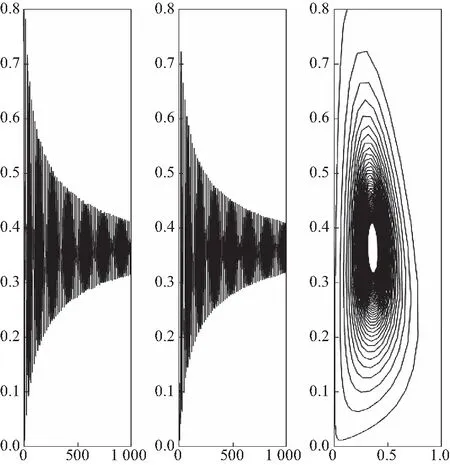
图2 当τ=3.35>τ0=2.633 2时，系统(24)的变化图和相图Fig.2 Variation diagram and phase orbit of system (24) when τ=3.35>τ0=2.633 2

4 结语

本文研究了一类具有时滞和收获项的Lesile-Gower捕食系统的动力学行为，考虑了捕食者种群的消化时滞和收获项对捕食系统种群的密度影响.研究结果表明，时滞的变化对系统的正平衡点的稳定性产生影响，当τ∈[0，τ0)时系统(24)的正平衡点是局部渐近稳定的；当τ>τ0时系统(2)正平衡点的稳定性被破坏.