面向新型电力系统的最小服务延迟的负载分配算法研究
张秋雨,蒋云峰,张常稳,张一鸣
(1. 国网河北省电力有限公司邢台供电分公司,河北 邢台 054000; 2. 华北电力大学科技学院,河北 保定 071051)
0 引 言
近两年来国家积极推动新型电力系统发展,建设以新能源为主体的新型电力系统,有效支撑为微网、分布式电源和新能源的大范围接入,打造多能互补、双向互动的能源互联网[1-2]。新型电力系统核心特征在于新能源占据主导地位,分布式能源大规模并网接入,成为主要能源形式,为有效提高新型电力系统能源利用率,进一步完善整个电力系统发电、输电、用电和储能环节的深度感知[3-5]。对低时延的要求非常高,其中配电网保护与控制、智能配电网微型同步测量都要求低于10 ms的超低时延,一些关键性的控制指令时延要求高达毫秒级。然而,在传统的云计算架构中,数据上传到远程云服务器需要消耗大量的传输时间,核心网有限的带宽难以承受海量的数据传输[6]。作为一种更接近业务端的新型计算技术,边缘计算已经成为处理延迟敏感业务的有效解决方案,推动新型电力系统能源互联网的发展步伐[7-9]。
文献[10]基于边缘计算技术的边缘处理能力,对配网业务的需求进行分析处理,有效提高业务处理能力,降低处理延时。文献[11]构建了基于云边协同的配电网络故障边缘网络架构,实现网络状态的实时监测,有效提高故障定位和隐患排查准确和时效性。文献[12]提出了一种基于机器学习的边缘智能任务卸载模式,通过对正常和故障情况下配电网络运行参数波形进行实时采集和比对分析,保证了配网运行实时和稳定性。文献[13]提出了一种基于边缘计算的配电网络拓扑结构的最小碰撞诊断算法,在云平台的边缘侧引入了边缘计算终端,并基于距离和处理任务对终端数据资源接入进行合理调度分配。文献[14]开发了一种数据驱动方法,完成配电网的初始故障检测和定位。
通过上述研究分析发现,边缘计算技术能够有效地缓解网络传输延时造成的电力运维和现场作业的风险。但随着新型电力系缘侧终端数量的急剧增加,仅依靠单个边缘设备依然无法完全满足所有电力业务的时延要求,同时由于边缘节点资源有限,单纯通过优化边缘节点资源分配来提高应用请求处理速率,对于网络时延的改善依然有限。基于上述问题方面,综合考虑边缘节点间和节点内的资源分配,研究了满足较低服务延迟的工作负载分配机制。依托网络时延和计算时延,构建了一个基于边缘智能的网络负载分配模型,以最小化新型电力系统负荷控制类业务总体传输延时。此外,为进一步降低多业务终端的服务时延,构建了一种网络负载资源分配模型。在初始化阶段,通过任务平衡算法来改善边缘节点间的工作负载平衡。为了有效保证资源分配的合理性,提出了一种改进的粒子群优化算法,对于边缘节点的CPU资源进行有效地分配。在分配的决策中,基于半定规划算法,将应用任务分配给边缘节点,实现网络资源的合理分配。
1 系统模型
随着新型电力系统的建设步伐的不断加快,各种终端设备的大范围接入,电网信息业务急剧增加,大量数据信息上传到远程云端处理器需耗费大量时间和带宽资源,对云端处理器的数据处理造成巨大的挑战,对此文中构建了基于边缘计算的新型电力系统通信网络架构如图1所示。分布式新能源发电、智能输配变电、储能和智慧用电等新型电力业务位于网络接入侧,基于各类传感设备完成各类业务状态的实时监控和灵活感知,并通过有线、4G、5G、电力无线专网等方式将边缘节点信息传输给边缘物联代理设备,承担远端云服务器最初需处理的部分或全部任务,完成数据的实时计算和智能存储,有效提高数据处理效率,降低任务处理延时。云端控制器基于典型业务数据需要,从边缘设备中实时调取相关数据,做到数据的灵活灵用,实时调取。
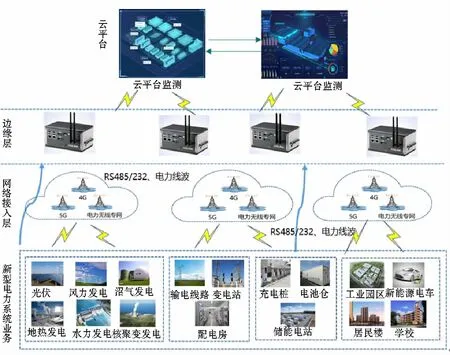
图1 基于边缘计算的新型电力系统通信网络架构Fig.1 New power system communication network architecture based on edge computing
1.1 基于边缘计算的新型电力业务负载分配模型
由于需要用户端(User Ends, UE)提供不同的业务,一个用户端运行新型电力系统业务,每种类型的业务请求都需要上传边缘节点(Edge Node, EN)通过不同的虚拟机(Virtual Machine, VM)对不同业务需求进行处理。为实现多业务资源的有效调度,有必要设计一种用户终端如何访问边缘节点的工作负载分配机制。提出的工作量分配模型如图2所示,在一个区域中,I为边缘节点的集合,J为用户端的集合,Kj为UEj中所有新型电力业务的总和。其中Kj是在UEj中运行的新型电力业务的集合,假设第k个新型电力业务的需求响应集合为wjk=[ljk,wjk]。ljk为任务总量,wjk为负荷工作量,服从泊松分布[15]。服务延迟被定义为从请求生成到请求在网络上完全处理时的时间,并且代表网络的服务时间。
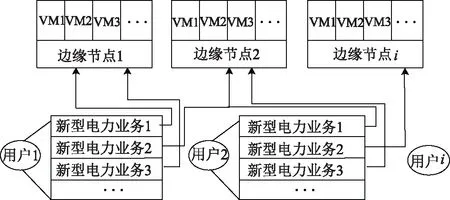
图2 任务分配模型Fig.2 Task allocation model
dijk代表延迟wjk,UEj的第k个业务请求分配给ENi。由此可见,UEj的任务分配是一个Kj→I映射问题。考虑所有的UE,所有新型电力业务的集合为K=∪j∈JKj,任务分配为J×K→I映射问题。因此,dj和dijk之间的关系可以表示如下:
(1)
其中xijk是一个二进制变量,如果wjk是分配给ENi,那么xijk=1,否则,xijk=0。
在边缘计算中,业务请求由用户设备生成,并通过网络信道传输到网元进行处理。因此,dijk分配给ENi的APPkUEj的延迟,包含了到ENi的网络延迟和业务请求在ENi中处理所消耗的计算延迟。
(2)
Bj为UEj的传输速率,rij为UEj和ENi之间的距离,c为传播速度。考虑无线电波的反射和绕射,假设模型分析中Bj足够大,这就有lijk/Bj≪rijk/c,所以接下来主要考虑网络延迟,忽略传输延迟。其网络延迟为:
(3)
计算延迟由EN的计算能力决定,vij为ENi处理第k个应用的CPU速率,则计算延迟为:
(4)
1.2 问题形成
V=(vik)×K为EN中VMs(虚拟机)资源分配向量。vik为VMk在ENi的处理速率,vi为边缘计算节点数据处理速度。基于网络实际运行现状,合理的调节和分配虚拟中的数据处理任务,可有效边缘节点的任务处理时延,达到最优,对其处理速度进行约束:
(5)
0≤vik≤vi
(6)
X=(xijk)I×J×K是一个三维数组,表示UE和EN中应用请求的映射关系,数组元素的值规定如下:

(7)
一个任务只能分配给一个EN进行处理,因此有以下限制:
(8)
为满足每个用户设备的服务质量要求,用户设备的服务延迟必须小于特定值。设Tj为UEj的服务延迟约束,即满足以下约束:
dj≤Tj
(9)
优化目标是P1。
(10)
此类问题为一种NP难问题,直接进行求解相对比较困难。
(11)
2 问题优化
解决P1的难点在于任务分配X依赖于EN中的资源分配V,而任务分配反过来又影响EN中的资源分配。为解决P1问题,提出了一种快速分配算法,将上述问题分解为三个子问题:均衡初始化、资源分配和任务分配。在初始化过程中,每个用户设备生成的应用请求被分配给网元。为了避免最近的进化网络因计算任务多而增加的计算延迟, 提出了一种面向网络负载均衡的传输机制。资源分配阶段,通过在遗传算法中引入信息素对传统粒子群算法进行改进。
2.1 平衡初始化
在不考虑数据处理时延的情况下,仅需要从数据传输的时延方面分析效率。即使rij(i∈I)最小,优化问题P1可表示为P2。
(12)
(13)
由于只考虑网络时延,所以与计算时延无关,也就是说可以忽略UE中新型电力业务的类型。P2的维度缩小了,相当于P2的问题。找到UE所有最近的EN作为阵列X=(xij)I×J的最优解X(0)。
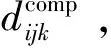
2.2 资源配置
通过平衡初始化,可以解决边缘节点(即P3)的计算资源分配问题。
0≤vik≤vi
(14)
为方便后续求解,需要对变量进行归一化处理,这里有vik/vi=pik,对应的矩阵为P,其中pik为VM中计算任务占整体处理任务的比重,因此求解问题可重新表示为:
(15)
提出了一种改进粒子群算法解决P3问题。该算法的本质就是基于有限迭代逐渐逼近问题的最小化和最大化函数,通过交叉求解的方式获得最优解。改进粒子群算法利用蚁群算法中的信息素保留所有粒子的最优经验信息,并影响粒子选择路径的速度,使算法能够快速收敛。
位置和速度是粒子群算法中两个基本参数,其中的每一粒子位置都对应一个可行解。资源分配矩阵为P∈,而速度定义为矩阵U∈。
U∈(n+1)=g(wU∈(n))+c1·r1(n)·(Pb∈(n)-
P∈(n))+c2·r2(n)·(Gb∈(n)-P∈(n))
(16)
式中Pb∈(n)、Gb∈(n)分别为n次迭代后粒子的个体和全局最优解。
根据式(17)更新位置:
P∈(n+1)=P∈(n)+U∈(n+1)
(17)
其中,uik∈[-umax,umax],umax为最大粒子速度。
(18)
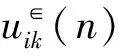
为了满足终端用户对低时延网络环境的需求,这部分的重点从降低系统的服务时延角度出发,则对应适应度函数可表示为:
(19)
为了防止基于传统PSO算法对网络性能进行优化,因粒子节点状态无法进行实时上传,分析容易陷入局部最优的风险。对此,在传统PSO算法的基础上将信息素考虑在内,基于想信息素浓度完成位置信息的更新。
基于式(20)完成信息素矩阵的更新:
T(n+1)=(1-ρ)T(n)+ΔT(n)
(20)
式中ρ是信息素挥发因子。
信息素增量矩阵表示为:
(21)
式中S为信息素的稠密程度;ε为种群规模。
为了有效反应信息素对网络路径选择的影响,这里通过引入转移概率概念:
(22)
式中φik(n)为第n次迭代后ENi处理k型应用的请求概率;ηik和β分别为启发因子和对应的权重;a为权重参数。
ηik由式(23)计算得出:
(23)
速度更新如下:
U∈(n+1)=g(wU∈(n))+c1·r1(n)·(Pb∈(n)-P∈(n))+c2·r2(n)·(Gb∈(n)-P∈(n))+φ(n)
(24)
MPSO算法的复杂度是不确定的,近似等于O(N×(I×K)+|ε|)。
2.3 任务分配
在解决边缘节点资源分配问题后,将原来的工作量分配问题简化为任务使用目的分配问题,如问题P4:
(25)

(26)
为了简化问题分析的复杂性,将P4的问题可以转化为一个等价的问题。通过减少秩1约束,将问题转化为齐次半定规划,二元约束可以用二次约束代替。
x(x-1)⟺x∈{0,1}
(27)
X和ψ表示为一维向量,如下所示:
X=[x111, …,xI11,x121, …,xI21,x1J1, …,xIJ1,
x112,…,xI12,x122, …,xI22,x1J2, …,xIJ2, …,x11K, …,xI1K,x121K,…,xI2K,x1JK, …,xIJK]T
(28)
ψ=[ψ1,ψ2,…,ψJ]T
(29)
定义一个新的变量y=[XTψT]T,其元素yi满足约束(30):
yi(yi-1)=0 ⟺yi∈{0,1},i=1,2,…,
(I×J×K)
(30)
然后,P4的可以转换成P5:
(31)
up是一个(I×J×K+J)维向量,其第p个维度对应的数值为1,其他元素的值全部为0。diag(up)是由up作为对角中的元素构成的(I×J×K)×(I×J×K)维对角矩阵。
其他符号解释如下:
(32)
(33)
b2=[T1T2....TJ]T
(34)
(35)
A1=[B1-B2]
(36)
A2=[0I×J×K-EJ×J]
(37)
A3=[diag(11×I...11×I)(J×K)×(I×J×K)0I×J×K]
(38)
(39)
B2=diag(V…V)(I×J×K)×J
(40)
B3=diag(W1…WK)(I×K)×(I×J×K)
(41)
Wk=[W1k…WJk]I×(I×J)
(42)
Wjk=wjkEI
(43)
V=[v11,...,vI1,v12,...,vI2,...,v1K,...,vIK]T
(44)
定义Z=[yT1]T[yT1]和Q=I×J×K+J,对问题P5进行变换转化为P6:
(45)
等式中的符号如下:
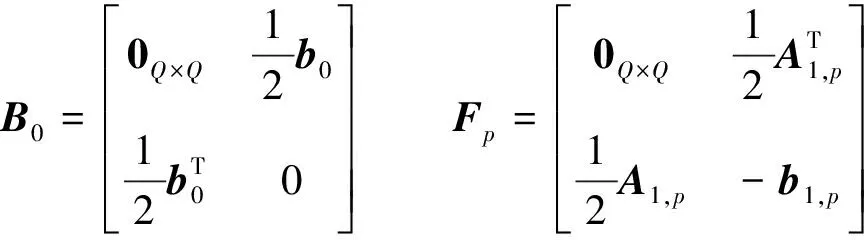
ZQ+1,Q+1是矩阵Z的第(Q+1)行和第(Q+1)列元素。A1,p、A2,t、A3,j分别为矩阵A1、A2和A3对应p,t和j行向量。
Z*是最优解,利用CVX凸优化工具包忽略秩-1约束,如果Z*满足秩-1约束,P4的最优解可以从Z*得到。
从Z*的左上角(I×J×K)×(I×J×K)矩阵中提取的Z′=x*x*T。由于xijk∈{0,1},因而xijkxijk=xijk,x*可以由Z′的对角线构造,工作负荷分配矩阵X*可以通过使用“整形”运算转换x*得到。
L为样本数量,(l)为样本指数。通过高斯变换,对Z*不满足条件进行分析。
算法3总结了所提出的算法。通过提取左上角的(I×J×K)×(I×J×K)子矩阵Z′作为协方差矩阵,生成L个随机(I×J×K)×1维向量。[0.68L]表示向下舍入,对应的分布函数可表示为:
(46)
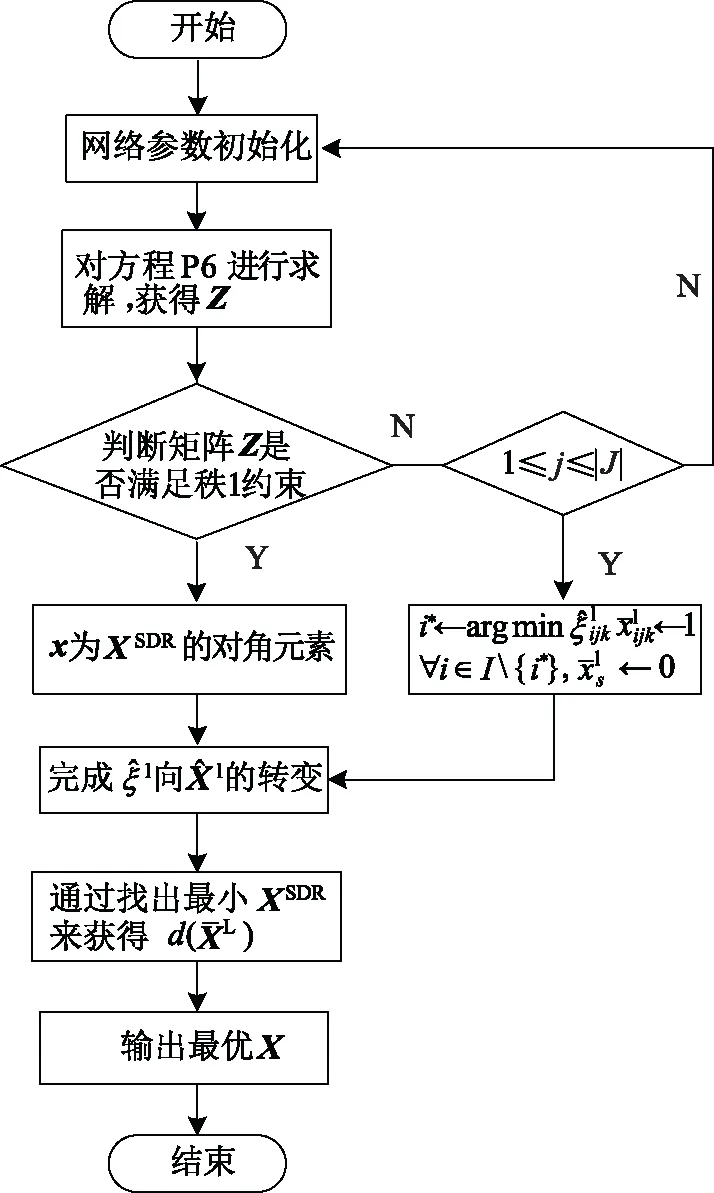
图3 基于SDR和高斯随机的算法流程Fig.3 Algorithm flow based on SDR and Gaussian random
3 仿真结果分析
搭建仿真环境对提出的算法进行测试验证。对于边缘计算系统的仿真参数设置,将物理环境为设置为边长为5 km的正方形区域。其中EN的数量为20,UE的数量为50~200[16-17]。为了保证结果的合理性,将EN和UE这两个参数的距离范围控制在1 km以内。此外,ENs和UEs采用无线的方式进行连接,传输速度为54 Mb/s~300 Mb/s[18]。新型电力业务存在6种不同的类型,不同类型的新型电力业务将采用不同的UE,从而生成对应的请求命令。同时,为了突出所提出的基于SDR算法的有效性,与文献[19-21]的卸载算法进行比对分析。
图4为边缘计算节点基于平衡和最近策略的计算时间。从仿真结果中可以发现,距离用户较近的边缘节点计算时延相对较大。因为考虑到系统的整体时延,为降低信息传输时延,将更多的工作任务分配给较近的边缘节点进行处理。对此利用所提出的平衡策略能综合考虑用户的计算和传输时延,对任务进行合理分配。实验结果表明,所提出的平衡策略能够有效缩小各边缘节点的计算上的耗时差异,从而在整体上提高计算效率。
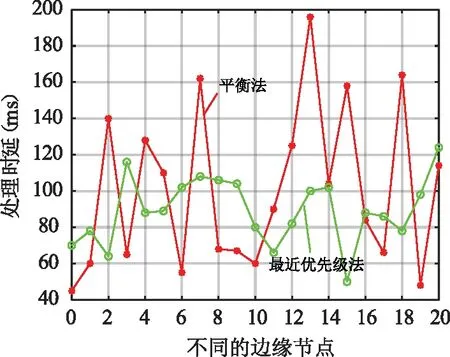
图4 平衡策略和最近策略初始化时ENs的计算时间Fig.4 Calculation time of ENs when the balance strategy and the most recent strategy are initialized
图5为不同算法收敛性的对比分析,通过对比分析发现所提出的图5为不同算法收敛性的对比分析,通过对比分析发现所提出的改进粒子群算法(MPSO)[22]相比于蚁群算法(ACO)[23]和传统粒子群算法(PSO)[24]能够实现快速收敛,同时基于信息共享的策略防止算法陷入局部最优的缺陷,通过对比分析发现MPSO算法的收敛时间比蚁群算法短7.4%。在优化效果方面,与粒子群算法相比,MPSO算法的服务时间减少了18.7%。
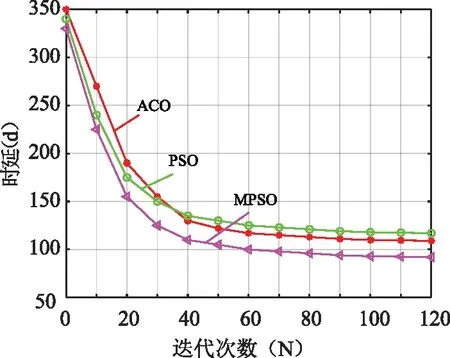
图5 资源分配中应用MPSO、粒子群、蚁群 算法的服务时间Fig.5 Service time of MPSO, particle swarm and ant colony algorithm lied in resource allocation
图6为算法准确性与高斯随机变量之间的关系。可以看出,随着高斯随机变量数的增加,相比与其他算法,SDR的解更接近真实解,误差更低。同时仿真结果可以看出,随机变量接入数量的增加可以显著降低求解误差这是因为当随机变量的个数超过问题的约束个数时,可以充分满足求解问题的需要,获得更精确的结果。

图6 结果准确性比高斯变量数量间的关系Fig.6 Relationship between the accuracy of the results and the number of Gaussian variables
图7对比分析了新型电力终端接入数量对系统服务时延的影响,从图7中可以看出,服务时延随新型电力系统业务接入数量的增加会不断的加大。所提出的BRT边缘节点资源分配算法,相较于SAA算法[25]服务延迟降低了9.1%。同时,通过对比分析发现,在相同的终端新型电力业务接入数量下所提出的边缘计算方式相对传统的集中式云计算方式,系统的服务时延得到明显的改善。
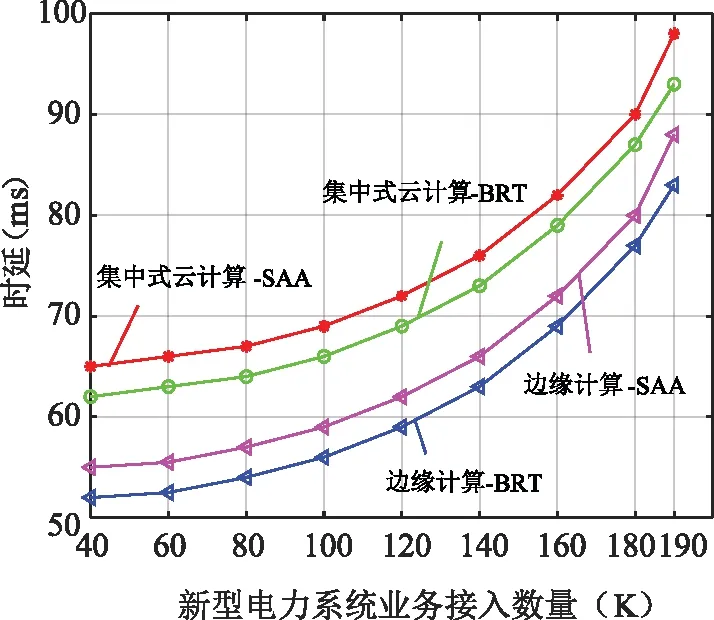
图7 新型电力业务接入数量与服务时延之间的关系Fig.7 Relationship between the access number of new power businesses and the service delay
图8为服务时延与新型电力业务接入数量之间的关系。从图8中可以看出系统服务时延与新型电力业务接入数量大概成线性关系,LEAD算法的增长率最大,因为它无法区分不同类型应用请求的延迟要求。LAB算法可以协调计算量大的应用请求和计算量小的应用请求,因此增长速度稍慢。SAA算法的服务时延绝对值小于LAB,但由于多种类型的应用请求之间没有区别,因此增长率仍然没有降低。所提出的BRT算法能够将不同类型的业务请求分配给边缘节点上对应的虚拟机,不仅实现了边缘节点间的应用请求分配,还优化了边缘节点内的计算资源分配。因此,增长率较小。

图8 不同数量新型电力业务的服务时间Fig.8 Service hours of different numbers of new power businesses
4 结束语
在新型电力系统建设过程中资源有限的单一边缘节点的固有特性已无法满足大规模接入的新型电力业务的延迟要求。对此文章研究了一种基于边缘智能的新型电力系统最小服务延迟的负载分配模型,推导出在信息传输速率和最大任务总量等约束条件下的系统传输时延,将目标函数转化为单目标问题分别求解,为了避免最近的进化网络因计算任务多而增加的计算延迟, 提出了一种面向网络负载均衡的传输机制。通过在遗传算法中引入信息素对传统粒子群算法进行改进,有效降低资源分配过程中的处理时延。仿真结果表明:与其他资源调度算法相比,无论是在系统时延还是算法收敛性方面都具有明显的优势。下一步,针对不同形态的业务类型可开展制定化的低时延边缘处理方案研究,并通过聚类分析完成业务类型的递归分类。

