新型混合型磁控电抗器的特性研究
赵国生,张高升
(郑州大学 电气工程学院,郑州 450001)
0 引 言
随着炼钢电弧炉、电气化铁路等冲击性负荷的不断接入,导致电网电压波动频繁,电能质量下降等问题。磁控电抗器具有连续可调、可靠性高、维护简便等特点,在电力系统中具有调节无功的作用,并能抑制系统过电压,抑制电网电压闪变等,对于提高电网经济性有着重要的意义[1-8]。目前对于磁控电抗器的研究主要基于饱和式磁控电抗器、单级磁控电抗器、双级磁控电抗器以及快速响应磁控电抗器。饱和式磁控电抗器响应速度慢,不能满足电网对无功补偿装置快速性的要求,且谐波含量较高,单级磁控电抗器,特别是双级磁控电抗器,虽然响应速度较于饱和式磁控电抗器有了明显的提高,但是单级磁控电抗器和双级磁控电抗器的磁阀部分已接近饱和[9-11],而铁芯部分磁通密度较低,必须增加线圈绕组的匝数,从而导致铁芯损耗的增加,快速响应磁阀式可控电抗器虽然能满足电网对于快速性的要求,但是由于单独增加了快速响应装置,增加了其控制精度和难度,且成本也大大增加[12-14]。
为了解决以上问题,设计了一种新型混合型磁控电抗器,在电网中采用该磁控电抗器作为静止无功补偿设备,可大大减小线圈匝数,从而减小磁控电抗器的功率损耗,减少发热,并可减小电抗器的谐波电流含量。采用了Maxwell与Simplorer联合实现场路耦合多物理域仿真分析,得到工作电流分析,并采用Matlab/Simulink软件分析其谐波含量,从而证明该磁控电抗器损耗小、谐波含量低的特点。
1 新型混合型磁控电抗器模型及其工作原理
1.1 新型混合型磁控电抗器模型
新型混合型磁控电抗器的构造模型如图1所示,该混合型磁控电抗器的铁芯结构采用三柱铁芯,两个边柱铁芯采用完全对称的铁芯结构,铁芯柱面积为Ab,长度为l,每个边柱铁芯柱中间都有一段面积缩小的部分构成磁阀,中间铁芯柱面积相等,不含磁阀。中间铁芯柱中有一个绕组,绕组匝数为N/2匝,两个边柱铁芯磁阀上下分别有一个绕组,共四个绕组,每个绕组的线圈匝数为N/2匝。其中,左铁芯柱的上绕组有一分接头(其抽头比δ=N2/N),左铁芯柱下绕组的初始端有一分接头,两分接头之间通过晶闸管KT1连接。右铁芯柱的下绕组有一分接头(其抽头比δ=N2/N),右铁芯柱上绕组的末尾端有一分接头,两分接头之间通过晶闸管KT2连接。左上绕组与右下绕组,右上绕组与左下绕组交叉连接,左上绕组末尾端与右上绕组末尾端通过续流二极管D连接。两边柱铁芯绕组并联然后与中间铁芯柱绕组串联接入电网的正弦交流电压源[15-19]。

图1 混合型磁控电抗器模型Fig.1 Model of a novel hybrid magnetically controlled reactor
1.2 新型混合型磁控电抗器的工作原理
新型混合型磁控电抗器的电路原理图如图2所示。混合型磁控电抗器是由一个铁芯电抗器和一个磁阀式可控电抗器串联而成。当混合型磁控电抗器接入正弦交流电源e=Emsin(ωt),如果晶闸管KT1与KT2均不触发导通时,电抗器中不产生自耦电流,磁饱和度为0,两边柱铁芯的绕组产生的感应电动势较小,但中间铁芯上的绕组(相当于一个电抗器)产生的感应电动势起到了分压与支撑作用,因此总的线圈匝数选取的很小。
当混合型磁控电抗器工作在额定工作状态时,由于两边柱铁芯所选取的线圈匝数小,使得磁阀部分的工作磁密明显降低,从而大大降低了磁控电抗器的铜耗与铁耗。
当0≤ωt≤π时,电源e是正向电压,若给晶闸管KT1施加触发脉冲,使KT1导通,当 π≤ωt≤2π时,电源e是反向电压,若给晶闸管KT2施加触发脉冲,使KT2导通,在交流正弦电源电压的完整周期内,晶闸管KT1、KT2的轮流导通与续流二极管D起到了整流的作用,使左上绕组与右上绕组,左下绕组与右下绕组分别流过相应的直流控制电流,中间柱不饱和铁芯上流过的交流磁通为两个边柱铁芯交流磁通之和,磁阀式可控电抗器的直流磁通不流过中间柱铁芯[20-23]。通过改变晶闸管触发角的大小,可以连续调节绕组中流过的直流电流,从而控制电抗器铁芯的磁饱和度,改变工作绕组中交流工作电流的大小来实现平滑调节混合型磁控电抗器的容量[24]。
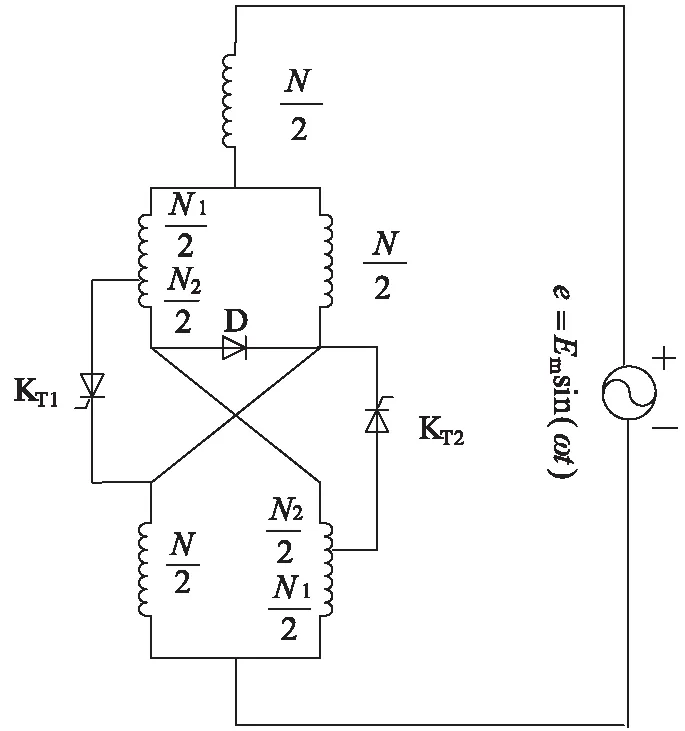
图2 混合型磁控电抗器的电路原理图Fig.2 Circuit diagram of a hybrid magnetically controlled reactor
2 新型混合型磁控电抗器的理论分析
2.1 电磁分析
新型混合型磁控电抗器的左右边柱铁芯的磁通向中间柱铁芯汇集,因此有Φ1+Φ2=Φ3。
当晶闸管不施加触发脉冲时,混合型磁控电抗器处于空载状态下,此时,混合型磁控电抗器的铁芯在一个周期内均处于不饱和状态,磁饱和度为0,磁阻较小,磁阀部分的磁阻较大,交流工作电流很小[25]。
当晶闸管KT1与KT2轮流导通时,对左铁芯与右铁芯及中间铁芯柱分别列磁动势方程如下:
(1)
由于磁阀部分磁阻远大于铁芯部分磁阻,因此,混合型磁控电抗器的磁势方程为:
(2)
下面推导新型混合型磁控电抗器的电磁方程,在此,晶闸管KT1、KT2及二极管D为理想器件,即它们导通时电阻为零,压降为零,截止时电阻无穷大。
根据晶闸管KT1、晶闸管KT2与二极管D的导通截止相互配合情况,共有五种不同的导通截止状态:
(1)晶闸管KT1导通,KT2截止,二极管D截止;
(2)晶闸管KT1导通,二极管D导通,晶闸管KT2截止;
(3)当二极管D导通时,晶闸管KT1截止,KT2截止;
(4)晶闸管KT2导通,KT1截止,二极管D截止;
(5)晶闸管KT2导通,二极管D导通,晶闸管KT1截止。
其中,由于状态4和状态5分别与状态1和状态2对称,因此,文章主要讨论前三种状态。
当晶闸管KT1导通,晶闸管KT2截止,二极管D截止时,根据回路电流法列混合型磁控电抗器电磁方程为:
(3)
解上述方程得,左铁芯柱和右铁芯柱的电磁方程为:
(4)
(5)
晶闸管KT1导通,晶闸管KT2截止,二极管D截止时,左铁芯柱的上下绕组流过的电流分别为:
(6)
(7)
右铁芯柱的上下绕组流过的电流分别为:
(8)
(9)
当晶闸管KT1导通,二极管D导通,晶闸管KT2截止时,根据回路电流法列混合型磁控电抗器电磁方程为:
(10)
解上述方程得,左铁芯柱和右铁芯柱的电磁方程为:
(11)
(12)
晶闸管KT1导通,二极管D导通,晶闸管KT2截止时,左铁芯柱的上下绕组流过的电流分别为:
(13)
(14)
右铁芯柱的上下绕组流过的电流分别为:
(15)
(16)
当二极管D导通时,晶闸管KT1截止,晶闸管KT2截止,根据回路电流法列混合型磁控电抗器电磁方程为:
(17)
解上述方程得,左铁芯柱和右铁芯柱的电磁方程为:
(18)
(19)
二极管D导通时,晶闸管KT1截止,晶闸管KT2截止时,左铁芯柱的上下绕组流过的电流分别为:
(20)
(21)
右铁芯柱的上下绕组流过的电流分别为:
(22)
(23)
式中F1为左边柱铁芯的磁势;F2为右边柱铁芯的磁势;F3为中间铁芯的磁势;Bt1为左边柱铁芯中磁阀段的磁密;Bt2为右边柱铁芯中磁阀段的磁密;f(Bt1)为左边柱铁芯中磁阀段的磁场强度;f(Bt2)为右边柱铁芯中磁阀段的磁场强度;Emsinωt为混合型磁控电控器两端所加的交流电源电压;μ0为空气磁导率;Ab为半铁芯的大截面段面积;Ab1为半铁芯的磁阀段面积。
2.2 谐波分析
在混合型磁控电抗器的两端加正弦交流电压e=Emsin(ωt),由于晶闸管KT1与KT2的导通状态具有对称性,根据谐波平衡原理,磁感应强度中的三次奇次谐波和偶次谐波含量很小,所以得到:
(24)
由电磁分析原理得,混合型磁控电抗器的工作电流为:
(25)
因为磁化曲线是奇函数,有:
(26)
联立上式得:
(27)
奇次谐波分量的幅值为:
(n=0,1,2,3…)
(28)
混合型磁控电抗器的基波和各次谐波的标幺值为:
(29)
混合型磁控电抗器从空载状态到饱和状态,输出的无功容量越来越大,磁通密度从零到极限饱和点,此时铁芯的饱和度成为额定饱和度。实际应用中,将混合型磁控电抗器从空载状态调到饱和状态,得到额定基波电流值,将其作为基准值,因此,各谐波电流的最大值与基准值的比值即可准确地反应混合型磁控电抗器的谐波特性。
3 混合型磁控电抗器的仿真分析
3.1 仿真模型的建立
Ansys作为工程数值仿真软件,是一款多用途有限元法分析软件。采用Ansys Maxwell软件建立混合型磁控电抗器仿真模型,模型结构图如图3所示、主要参数如下:铁芯长为720 mm,高为1 220 mm,厚度为140 mm,上下两铁轭高为160 mm,磁阀长度为60 mm,高为50 mm,线圈匝数为1 200匝,抽头比为0.1。文中的模型由AutoCad软件绘制,再导入Ansys Maxwell软件中。材料设置环节,绕组采用copper(铜)材料,铁芯材料采用M-4-30,其余配置为air(空气)。边界条件采用Ballon Boundary(气球边界条件)。激励源采用外部激励设置。求解设置中,仿真时间设置为10 s,仿真步长设置为1 ms。在Ansys Maxwell的瞬态场求解器Transient Solver中进行网格剖分设置,剖分采用自适应剖分参数。网格剖分图如图4所示。

图3 混合型磁控电抗器模型图Fig.3 Model diagram of a hybrid magnetically controlled reactor

图4 混合型磁控电抗器剖分图Fig.4 Grid division diagram of a hybrid magnetically controlled reactor
3.2 Simplorer 与Maxwell 联合仿真
采用Ansys Maxwell建立模型,Ansys Simplorer搭建仿真实验电路。Simplorer与Maxwell联合仿真的电路接线图如图5所示,其中,左上绕组与右下绕组,右上绕组与左下绕组交叉连接,左上绕组末尾端与右上绕组末尾端通过续流二极管D连接。两边柱铁芯绕组并联然后与中间铁芯柱绕组串联接入电网的正弦交流电压源。电路的主要参数如下:E1为单相正弦交流电压源,峰值电压为6.0 kV,频率为50 Hz,绕组上的电阻R1=R2=0.2 Ω,R3=0.02 Ω,电容C1=0.002 μF。PULSE1和PULSE2模块为晶闸管提供触发信号。改变PULSE1和PULSE2的时间参数即可改变晶闸管的导通时间,进而改变混合型磁控电抗器的直流控制电流和磁饱和度,改变磁控电抗器的工作电流。
3.3 工作电流特性分析
空载电流波形如图6所示。

图5 Simplorer与Maxwell联合仿真实验原理图Fig.5 Experiment schematic diagram of Simplorer and Maxwell joint simulation

图6 空载电流波形图Fig.6 No-load current waveform
在空载状态下,晶闸管KT1与KT2均不导通,此时,混合型磁控电抗器中不产生自耦电流,铁芯柱在一个工频周期内均处于不饱和状态,磁饱和度为0,磁阻较小,但磁阀部分磁阻较大,交流工作电流很小。此时,两边柱铁芯的绕组产生的感应电动势较小,但中间铁芯柱上的绕组(相当于一个电抗器)产生的感应电动势起到了分压与支撑作用,因此总的线圈匝数选取的很小。
当混合型磁控电抗器的晶闸管开始导通时,改变晶闸管的导通角,混合型磁控电抗器可以输出不同的工作电流。晶闸管的导通角是通过触发信号PULSE1和PULSE2的DELAY模块设定的,电压源频率为50 Hz,即周期为20 ms,触发信号设置为1 ms即晶闸管的导通角设置为18°,触发信号设置为2 ms即晶闸管的导通角设置为36°,按此比例,即可设置晶闸管导通角为任意角度。通过改变晶闸管触发角的大小,可以连续调节绕组中流过的直流控制电流,从而控制电抗器铁芯的磁饱和度,改变工作绕组中交流工作电流的大小来实现平滑调节混合型磁控电抗器的容量。如图7~图11所示为混合型磁控电抗器的实验结果图,晶闸管的导通角为9°时,工作电流峰值为26.85 A,晶闸管的导通角为36°时,工作电流峰值为23.59 A,晶闸管的导通角为90°时,工作电流峰值为10.38 A,晶闸管的导通角为126°时,工作电流峰值为5.51 A,晶闸管的导通角为171°时,磁饱和度越大,直流控制电流越大,混合型磁控电抗器的工作电流也越大。因此,通过改变晶闸管触发角的大小,可以连续调节绕组中流过的直流电流,从而控制电抗器铁芯的磁饱和度,改变工作绕组中交流工作电流的大小来实现平滑调节混合型磁控电抗器的容量。

图7 晶闸管导通角为9°时的工作电流波形图Fig.7 Operating current waveform when the thyristor conduction angle is 9 degrees

图8 晶闸管导通角为36°时的工作电流波形图Fig.8 Operating current waveform when the thyristor conduction angle is 36 degrees
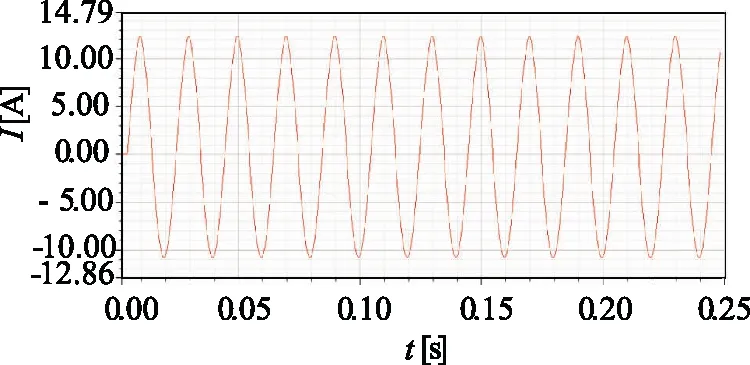
图9 晶闸管导通角为90°时的工作电流波形图Fig.9 Operating current waveform when the thyristor conduction angle is 90 degrees

图10 晶闸管导通角为126°时的工作电流波形图Fig.10 Operating current waveform when the thyristor conduction angle is 126 degrees

图11 晶闸管导通角为171°时的工作电流波形图Fig.11 Operating current waveform when the thyristor conduction angle is 171 degrees
3.4 谐波特性分析
用Matlab/Simulink对新型混合型磁控电抗器做谐波分析,由9°的谐波分析图可得出,此时,偶次谐波和三次及以上谐波的含量均较少,符合混合型磁控电抗器的谐波分析结论。由图12~图16可知,晶闸管导通角为9°时,波形畸变率为2.69%,晶闸管导通角为36°时,波形畸变率为4.67%,晶闸管导通角为90°时,波形畸变率为8.93%,晶闸管导通角为126°时,波形畸变率为36.31%,晶闸管导通角为171°时,波形畸变率为111.98%。因此,混合型磁控电抗器随着晶闸管导通角的变大,工作电流减小,谐波含量升高。在晶闸管导通角为9°时,混合型磁控电抗器的谐波含量较低,此时混合型磁控电抗器工作于接近满载的状态。因此,混合型磁控电抗器应尽量工作在满载或接近满载状态下,当混合型磁控电抗器工作于满载状态时,相应的磁饱和度为2π,因此,满载状态也叫极限饱和状态,同时,可将极限饱和状态作为混合型磁控电抗器的额定工作状态。
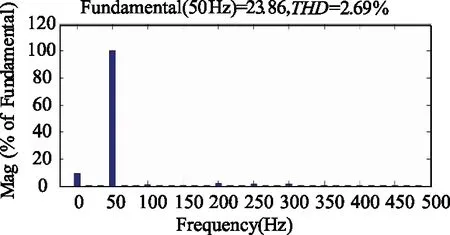
图12 晶闸管导通角为9°时的谐波分析图Fig.12 Harmonic analysis diagram when the thyristor conduction angle is 9 degrees

图13 晶闸管导通角为36°时的谐波分析图Fig.13 Harmonic analysis diagram when the thyristor conduction angle is 36 degrees

图14 晶闸管导通角为90°时的谐波分析图Fig.14 Harmonic analysis diagram when the thyristor conduction angle is 90 degrees

图15 晶闸管导通角为126°时的谐波分析图Fig.15 Harmonic analysis diagram when the thyristor conduction angle is 126 degrees

图16 晶闸管导通角为171°时的谐波分析图Fig.16 Harmonic analysis diagram when the thyristor conduction angle is 171 degrees
4 结束语
提出了一种新型混合型磁控电抗器的模型结构,并介绍了混合型磁控电抗器的铁芯结构和绕组构成,分析了其工作原理、电磁方程及谐波特性。用Ansys Maxwell有限元软件建立了混合型磁控电抗器的仿真模型,并采用Simplorer与Maxwell联合仿真搭建实验电路,通过对其工作电流波形和谐波含量进行分析,得出如下结论:新型混合型磁控电抗器采用磁阀式可控电抗器与不饱和铁芯电抗器线圈串联技术,中间柱不饱和铁芯上流过的交流磁通为两个边柱铁芯交流磁通之和,磁阀式可控电抗器的直流磁通不流过中间柱铁芯。该结构可以大大减小磁阀式电抗器的线圈匝数,从而减小磁控电抗器的功率损耗,减少发热,可以抑制可控电抗器的谐波电流。通过改变晶闸管的触发角,连续平滑调节混合型磁控电抗器的工作电流及容量,使磁控电抗器的电感值发生改变。混合型磁控电抗器由于匝数较小,铜耗和铁耗较小,因此可以有效地降低成本,提高经济性。

