HIV-1整合酶链转移抑制剂的QSAR研究与分子设计

陈 艳,冯 惠,周 俊,堵锡华

(徐州工程学院 材料与化学工程学院,江苏 徐州 221018)

整合酶(Integrase,IN)是人类免疫缺陷病毒1型(Human immunodeficiency virus-1)完整生命周期的必须催化酶之一,其机理是将逆转录酶产生的病毒脱氧核糖核酸(Deoxyribonucleic acid,DNA)整合到宿主染色体中,从而使HIV-1完成生命周期,所以以整合酶为靶点的抗HIV-1药物的研究成为了近几年的热点。目前整合酶抑制剂的筛选主要以链转移反应为靶标,称为整合酶链转移抑制剂(Integrase strand transfer inhibitors,INSTIs)。然而,用INSTIs治疗时,IN会发生突变,使HIV-1病毒产生耐药性,因此进一步开发抗突变性、抗耐药性、安全有效的新型HIV INSTIs变得迫在眉睫[1]。Zhao等[2]设计合成了一系列1,8-二氮杂萘-3-甲酰胺衍生物,并修饰了该系列化合物4号位和7号位,同时探索了6位取代基对抗病毒效应和抗耐药性2个方面的影响,得到了一系列活性数据。刘冬琳等[3]采用三维定量构效关系(Three dimensions-quantitative structure-activity relationship,3D-QSAR)、分子对接和分子动力学模拟等方法研究了该类化合物结构与活性的关系,取得了较好的结果。

本文在文献[4-10]工作的基础上,基于INSTIs的活性,运用多元线性回归中最佳变量子集回归的方法,筛选变量的最佳组合,建立多元线性定量构效关系(QSAR)模型,并把该最佳变量组合作为人工神经网络的输入层,建立反向传播(Back propagation,BP)算法模型,以期使相关性、预测能力更优,籍以探讨影响HIV-1 INSTIs生物活性的主要因素。

1 理论与方法

1.1 INSTIs的抑制活性数据

32个INSTIs(1,8-二氮杂萘-3-甲酰胺类衍生物)的分子结构及活性均来自于文献[3](活性值IC50的单位为nmol/L),其骨架见图1,其中R4、R6和R7分别代表4位、6位和7位上的取代基,具体分子构成见表1。

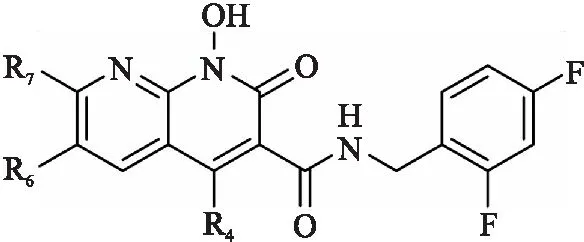
图1 INSTIs的分子骨架图

1.2 研究方法

1.2.1 分子描述符的计算

通常1个指数反映分子结构的信息量是有限的,往往需要多种指数联合。电拓扑状态指数Ei能够表征分子中所蕴含的电子与拓扑特征,电性距离矢量Mj是基于每一个非氢原子的拓扑环境及成键原子的电子信息通过矩阵运算得到的1组数值,所以这2个指数联合全面表征了分子的拓扑、几何及电性特征。具体的计算方法是用ChemDraw Ultra 9.0 软件分别构建32个1,8-二氮杂萘-3-甲酰胺类衍生物的分子结构,应用文献[11,12]的方法编制程序进行计算,得到46种电拓扑状态指数和91种电性距离矢量,去掉全为0的自变量,还剩57种分子描述符来表征INSTIs的分子结构。

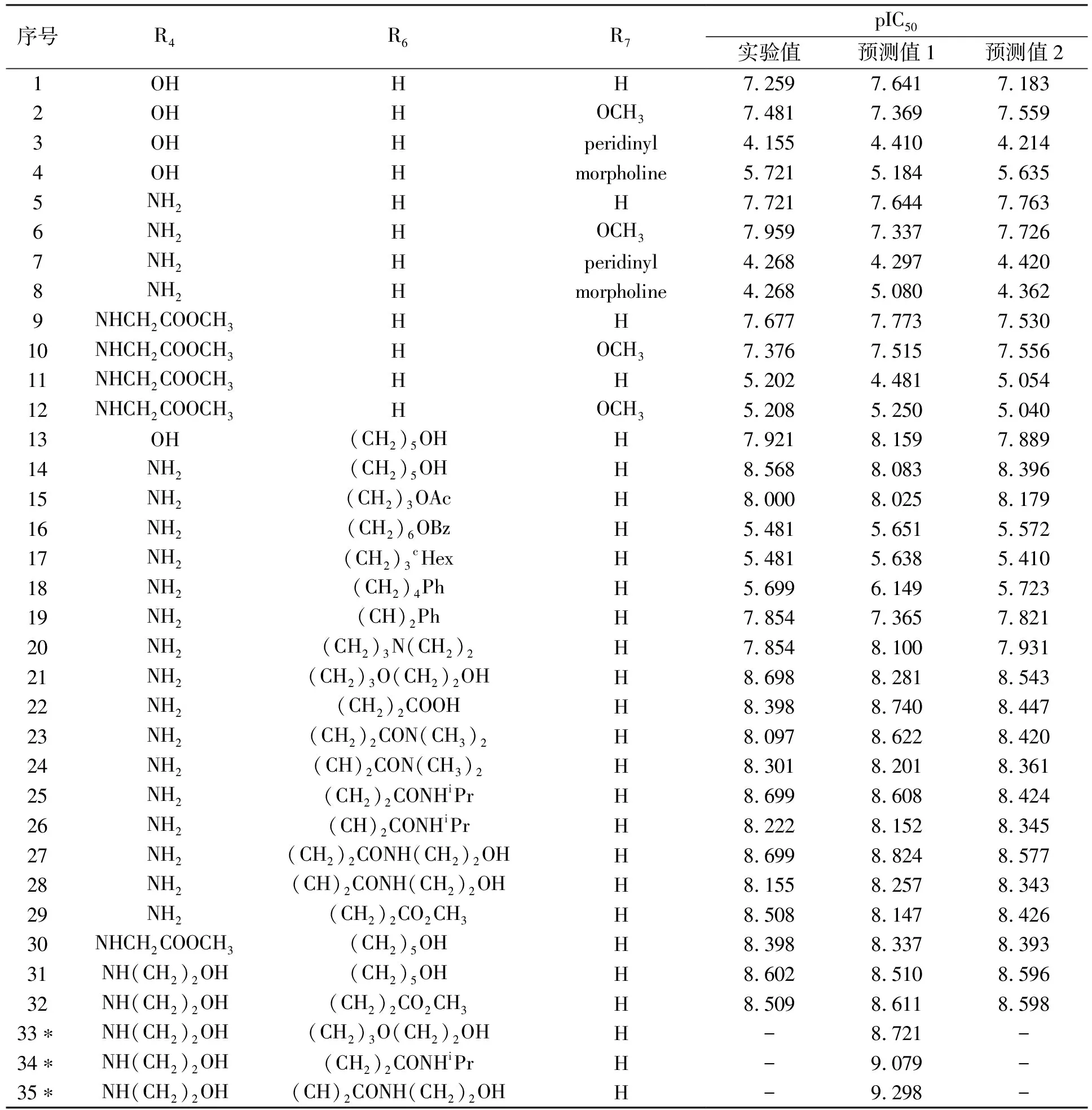
表1 INSTIs的分子结构及活性值表

*为设计的分子

1.2.2 多元线性回归分析和神经网络分析

将INSTIs的抑制活性(pIC50)和上文得到的57个分子描述符组成数据集,采用最佳变量子集回归的方法筛选最佳变量组合,建立多元线性回归模型,以Kubinyi函数(Kubinyi function,FIT)[13,14]做为选择最佳变量组合的依据,其计算公式为

(1)

式中:y为化合物数;b为变量数。FIT值的大小与模型的稳定性及预测能力成正比。

采用多元线性回归中的最佳变量组合作为神经网络的输入层,利用目前应用最为广泛的基于误差BP算法的人工神经网络建立模型,所建模型的相关性和预测能力均显著提高。

2 结果与讨论

2.1 多元线性回归模型的建立

表2 INSTIs抑制活性与En、Mj的最佳变量子集回归结果表

由表2可知,随着进入模型的自变量数目的增加,F和FIT逐渐增加,但后面4项指标均在第6个模型处出现拐点,说明(M57,M14,E7,E13,E21,M36)为最佳变量组合,最佳模型为

pIC50=(2.771±0.627)-(3.298±0.419)M57-

(0.192±0.026)M14+(0.401±0.082)E7+

(0.111±0.022)E13+(19.127±4.840)E21-

(4.628±1.573)M36

(2)

用模型式(2)计算32个INSTIs的抑制活性,得到的预测值1列于表1,该预测值和实验值基本接近,平均误差为0.264。

用Jackknife法[15]对模型进行稳健性检验。每次从32个化合物中去掉化合物序数中个位分别是0,1,2,3,…,9的分子,剩余化合物为建模组,根据模型式(2)进行回归,重复10次,得到10个R值,对这10个R值做控制图,见图2。可以看出,这10个点均在控制区域内,说明模型式(2)具有一定的稳定性。

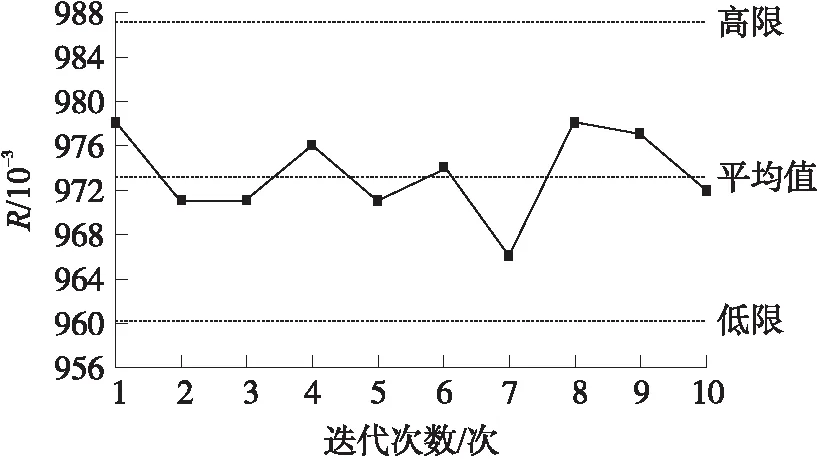
图2 Jackknifed相关系数控制图

2.2 神经网络分析

模型式(2)的交叉验证相关系数已经超过文献[3],但相关系数还略低,且用多元线性回归模型得到的预测值和实验值的平均误差偏大,所以用神经网络予以提升。

本研究采用BP算法构建预测INSTIs的抑制活性的神经网络模型,其输入层为6个最佳变量组合(M57,M14,E7,E13,E21,M36),输出层为INSTIs的抑制活性pIC50,为了避免出现过拟合、过训练现象,采用许碌规则[16]寻找最佳隐蔽层的单元数H,即

2.2>ρ(=N/M)≥1.4

(3)

式中:N、M分别是样本数和网络总权重。

M=(I+1)H+(H+1)Q

(4)

式中:I、H、Q分别是输入层、隐蔽层和输出层的单元数。本文的I=6,Q=1,N=32,可得1.693

图3 INSTIs分子抑制活性的实验值与预测值关系图

在建模时将数据分成3个集:每5个数据为1组,其中每组的第2、4、5个数据构成训练集,第1个数据构成测试集,第3个数据构成验证集,这样3个集的样本数分别为19、7和6。由此建立的BP模型为:Rtr=0.996,Rte=0.996,Rv=0.998,整体的R=0.996,可以看出训练集、测试集和验证集的相关系数均与总体的相关系数非常接近,说明所建模型稳健性较理想。给出的预测值2见表2,与实验值接近,平均误差为0.117,预测精度优于多元线性回归。2种方法所得到的预测值和实验值的相关图见图3,可以看出红点比黑点更接近对角线。

2.3 模型的分析及分子设计

3 结束语

基于电拓扑状态指数和分子电性距离矢量,通过多元线性回归的方法对32个INSTIs分子抑制活性进行了定量构效研究,得到如下结论:

(1)电拓扑状态指数和分子电性距离矢量联合共同表征了INSTIs分子的结构特征。

(2)采用最佳变量子集回归的方法,确定了(M57,M14,E7,E13,E21,M36)为最佳变量组合,BP神经网络模型得到的相关系数高于多元线性回归得到的相关系数,说明INSTIs分子的抑制活性(pIC50)与(M57,M14,E7,E13,E21,M36)之间具有良好的非线性关系。