基于水波优化算法的无线传感器网络覆盖研究
王 毅,神显豪,唐超尘,3,曹惠茹,刘 敏
(1.广州工程技术职业学院 信息工程学院,广东 广州 510075;2.桂林理工大学 信息科学与工程学院,广西 桂林 541004;3.西安电子科技大学 通信工程学院,陕西 西安 710071;4.西南石油大学 信息学院,四川 成都 610500)
无线传感器网络(Wireless sensor network,WSN)凭借其布网方便且组网灵活等优势广泛用于各种物联网领域。WSN可以满足大规模物联网设备的连网需要,但是由于WSN的节点数量众多,WSN应用的组网问题和能耗问题变得严峻[1]。为了满足WSN监测需要,在待监测的目标区域内需要实现网络感知的全覆盖,根据单个节点的感知范围和监测区域内的目标节点数计算所需要的传感节点数。一般将区域覆盖率作为评价的主要标准,通过优化算法对传感节点进行坐标优化部署,用尽可能少的传感节点来保证区域覆盖率需求,降低传感节点冗余率。
当前,关于WSN的节点覆盖的研究较多。徐钦帅等[2]采用蚁狮算法对WSN进行覆盖优化,并进行了效率改进,能够获得较高的覆盖率性能;王振东等[3]采用改进差分算法进行WSN覆盖,通过节点参数差分运算进行WSN节点定位,能够实现小规模节点精确定位;张亮等[4]采用模糊粒子群进行WSN节点定位,虽能够满足大区域节点定位覆盖,但优化性能并不高。
作为近期提出的一种基于浅水波理论的新型智能进化算法,水波优化(Water wave optimization,WWO)算法能够模拟自然界浅水波的传播运动机制,相比于其他启发式群体智能优化算法,具有控制参数少、操作简单、容易实现等优点。Zhu等[5]利用多目标WWO算法来求解作业车间调度问题,获得了较好的优化效果。传感节点区域覆盖的优化问题与作业车间调度求解一样,其本质都是多目标优化问题,因此,本文尝试采用WWO算法对传感节点区域覆盖进行优化。以区域覆盖率为适应度函数,通过传感节点坐标集构建水波个体,执行水波的传播、折射和碎波操作,对传感节点坐标进行优化,以提高区域网络覆盖率。
1 无线传感器网络覆盖
无线传感器网络的节点部署过程中,根据需要覆盖的区域大小及区域内需要监测的目标节点数量,可以灵活采取覆盖方式,主要有点覆盖和区域覆盖2种方式,根据不同的覆盖方式选择合适的覆盖优化模型。
1.1 点覆盖与区域覆盖
点覆盖方式主要用于监测的目标区域小且节点固定的情况,通过在目标节点周围部署一定量的传感节点可以完成所有目标节点的监测。具体结构如图1所示。

图1 点覆盖结构图
在图1的待监测正方形区域内,分布了多个目标节点,需要进行传感监测,圆形代表每个传感节点的感知范围。在节点部署时,充分结合节点能耗及通讯数据量来选择合适数量的传感节点。图1中至少需要4个传感节点才能完成对目标区域所有目标节点的监测。这种监测方式称为局部监测,不适合区域内目标节点动态变化的情况。若目标节点数量不固定,可以考虑用区域覆盖的方式,在节点部署时对区域内所有像素点完成感知覆盖。区域覆盖根据区域面积和区域内的目标节点数来选择传感节点数,其要求是部署的传感节点的感知范围能够覆盖区域内的每一个像素坐标,实现区域内节点的全感知,其主要结构如图2所示。

图2 区域覆盖结构图
图2完成了正方形目标区域的全覆盖,图2中至少需要9个节点便能完成区域覆盖,根据通信数据量和能耗可以增加传感节点。在实际的无线传感器网络覆盖应用中,区域覆盖使用范围广泛,常被用于各种领域的无线传感器网络监测,因此本文以区域覆盖为研究对象,优化区域内的目标节点数。
1.2 数学模型
设需要进行传感节点布置的区域为二维平面Area,在区域上投放的传感节点数为N,每个节点的通信和感知半径分别为R和r,R=2r,传感节点集为Node={x1,x2,…xN},nodei={xi,yi,r},传感点坐标(xi,yi),将Area数字化离散为l×m个像素点,像素点坐标为p=(x,y),则2个节点的距离为[6]
(1)
像素点被传感节点nodei覆盖的概率P为
(2)
考虑到环境因素干扰,引入正态分布扰动,式(2)变为[7]
P(x,y,nodei)=
(3)
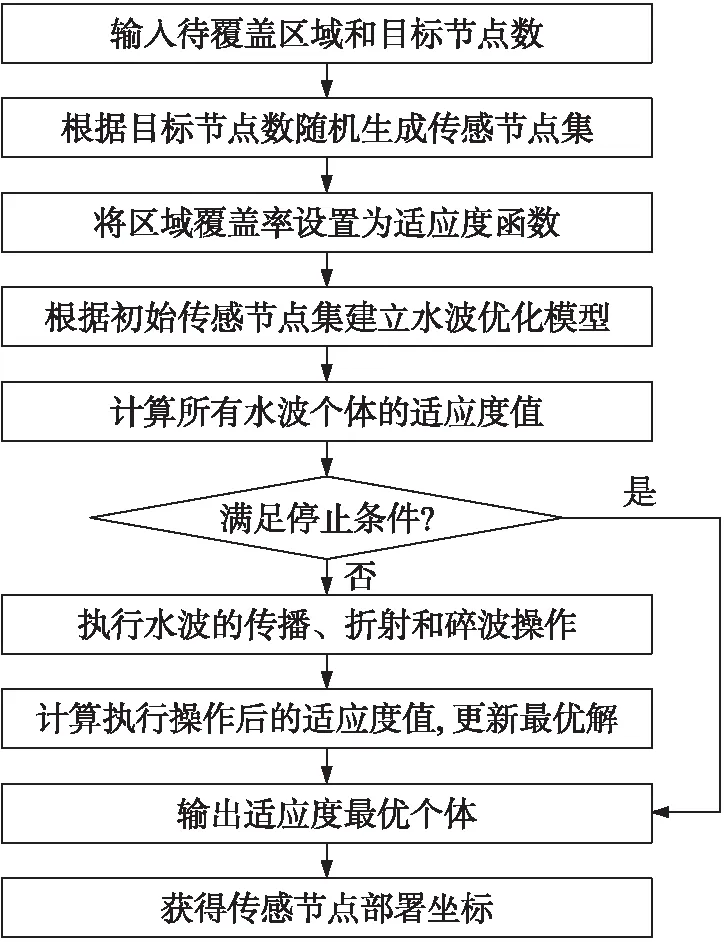
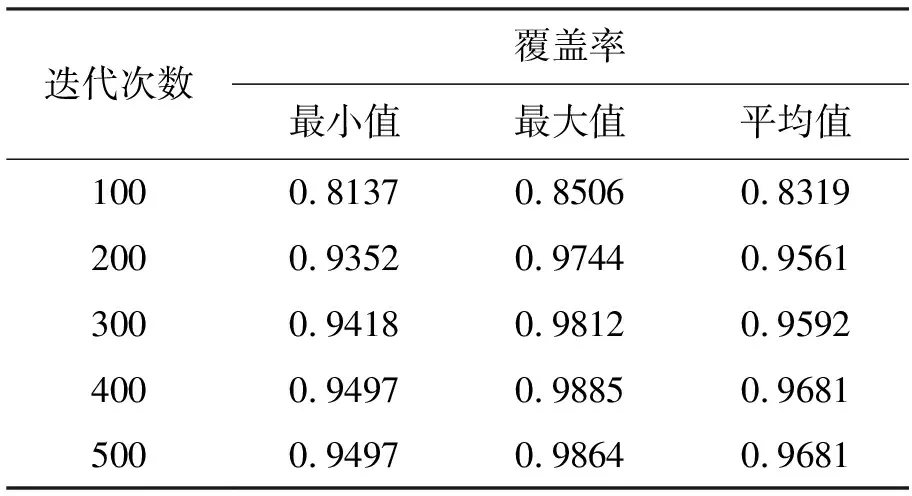
re(0 λ1=re-r+d(nodei,p) (4) λ2=re+r-d(nodei,p) (5) 在Area区域内像素被传感节点集覆盖的概率为 (6) 根据传感节点对像素节点的覆盖情况,可以求解传感节点对Area区域的覆盖率,计算方法为[8] (7) 在传感网络节点覆盖优化时,根据网络节点的能量及在感知范围一定的情况下,尽可能保证Rarea(Node)最大。 设问题解的维度为D,其中第d维水波x(d)执行一次传播得到x′(d),表示方法为[9] x′(d)=x(d)+rand(-1,1)·λL(d) (8) 式中:λ表示波长,L(d)表示第d维空间的搜索范围,rand(-1,1)是[-1,1]随机数,x′表示新水波。若f(x′)>f(x),则用x′代替原水波x,将x′的水波高度设置为hmax,否则不替换原x,单波高变为hmax-1,波长也发生变化,变化方式为[10] λ=λ·α-(f(x)-fmin+ε)/(fmax-fmin+ε) (9) 式中:fmax和fmin分别为适应度最大值和最小值,α表示水波衰减系数,为了防止出现fmin和fmax相等时式(9)无意义,引入ε参数,ε>0且无限趋近于0。 (10) x′的波高重新设置为hmax,波长更新方法为[12] (11) 在水波的能量不断蓄积过程中,波高不断增加,会发生碎波现象,1个水波会分解成多个独立波。随机选择D中的k维对水波x*执行碎波操作,产生的独立波位置更新方法为[13] x′(d)=x(d)+N(0,1)·βL(d) (12) 式中:β表示碎波系数,取值范围[0.001,0.01];L(d)表示第d维长度。计算所有独立波的适应度值,与水波x*的适应度值比较,取两者中的最大值作为新的最优水波x*。 采用传感器网络节点的网络覆盖率Rarea(Node)作为WWO的适应度函数f(x)。首先随机设置传感节点集坐标,每一组坐标作为1个水波Node。根据式(6)、(7)计算每个水波的适应度值,然后执行水波传播、折射和碎波操作。根据水波的位置变化不断更新适应度值,记录适应度值最大的水波节点。不断执行水波的运动操作,直至传感网络节点的覆盖率达到需求,或者更新迭代次数达到阈值。具体流程如图3所示。 图3 WWO的WSN节点覆盖流程图 为了验证WWO在无线传感器网络节点覆盖中的性能,进行实例仿真。仿真区域对象为60 m*60 m,传感节点参数r=5 m,N区间为[40,60],R=10 m,WWO默认迭代次数200。首先采用WWO对WSN传感节点的覆盖性能进行仿真;其次差异化设置N,验证不同N和迭代次数对应的覆盖性能;最后采用常用WSN覆盖算法和本文算法分别进行WSN节点覆盖仿真,对比不同算法的覆盖性能。 首先差异化设置N值,分别采用WWO对WSN进行节点覆盖仿真,其MATLAB的可视化覆盖结构如图4所示。从可视化的图4(e)发现,在未采用WWO算法进行节点部署之前,覆盖率较低,出现了较严重的区域内覆盖不均衡的情况,而图4(f)相比于其对应的图4(e),覆盖效果更好,所有节点能够较均匀地分布在区域内。横向对比发现,当N=50时,优化后的节点覆盖图最优;N=40时,区域内出现了较多未覆盖到的空白;而N=60时,虽然覆盖率有缓慢提升,但明显出现了节点冗余的情况,覆盖区域内出现了多处重叠。因此,从可视化图4中发现,选择N=50进行区域覆盖更加合适。 图4 MATLAB的可视化覆盖结构图 3.2.1 不同N的覆盖率 对不同N对应的覆盖率值进行仿真统计,结果如表1所示。 表1 不同N的覆盖率表 从表1可知,N对区域的覆盖性能影响明显,随着N增加,区域内的覆盖率提高。N从30增加至60时,覆盖率均值从0.665 8上升到了0.953 7。但当N大于50后,覆盖率的提升效果非常有限。N从50增加至60时,覆盖率均值仅提升了0.001 2,但是这10个节点数的增加明显提升了成本和能耗,因此选择N=50比较合适。 3.2.2 不同迭代次数的覆盖率 本文默认的迭代次数为200,前文仿真性能均为迭代次数为200的条件下获得的结果,现差异化设置迭代次数,N=50,验证覆盖性能。从表2可知,随着迭代次数的增加,覆盖率先增加后达到稳定。覆盖率最高均值为0.968 1。从表2可以判断,本文WWO覆盖算法的收敛次数为300~400。 表2 不同迭代次数的覆盖率表 为了进一步验证本文算法在WSN覆盖中的性能,分别采用蚁群[14]、人工鱼群[15]、粒子群[16]算法和本文WWO覆盖算法对60 m*60 m区域进行覆盖性能仿真,N=50,r=5 m,仿真结果如图5所示。 图5 4种不同算法的覆盖率性能图 从图5得,在覆盖率性能方面,本文算法最优,达到稳定时可以获得95%左右的区域覆盖率,粒子群次之,蚁群算法最差。从收敛性能方面看,蚁群算法最快,本文算法次之。综合比较,本文算法相比于其他3种WSN覆盖优化算法,具有更优的覆盖性能。 采用WWO算法应用于WSN节点覆盖,能够获得较高的区域覆盖率。选择合适数量的传感节点数和WWO迭代次数,相比于常用WSN节点覆盖优化算法,本文算法能够获得更高的覆盖率性能。后续研究将进一步优化WWO覆盖算法关键步骤,以进一步提高节点覆盖优化效率,提高大规模WSN节点布网的适用性。2 基于WWO的传感器网络节点覆盖
2.1 WWO
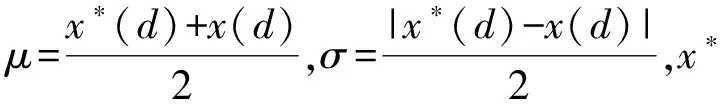
2.2 WWO的传感节点覆盖流程
3 实验仿真
3.1 传感节点覆盖可视化

3.2 不同N的覆盖性能

3.3 不同算法的覆盖性能

4 结束语

