网络环境下学生自主学习概率论能力的培养

曹晓春 荆文君 王艳梅

山西财经大学，山西 太原 030006

随着信息化技术的发展，网络、平板、手机等新型媒体深刻地改变着我们的学习和生活方式。高校学生作为受教育程度较高的主体，容易接受新事物、思想活跃，新型媒体对于他们来说已是飞入寻常“百姓家”。新型媒体尤其是网络对传统的教学产生了深刻的变革：以前是教师在课堂上占主导地位，学生被动地听，两者之间沟通和互动较少，而现在师生可以随地在QQ、微信等上面快捷方便地交流和互动，老师能及时解决学生问题；学生还可以根据学科和自身需要随时利用工具查阅学习信息，实现移动学习；网络环境下的学习需要学生更加积极主动地参与，使得学生学习自主性有了更大的主观能动性；网络环境下的学习能给学生营造一种宽松自由的学习环境，能使得学生充分发挥他们的聪明才干；网络环境下的学习使得学生不迷信老师，可以培养学生的独立思考能力，使之能批判地、创造性地学习。如何有效利用网络的便利性和灵活性，结合传统教学模式，创立与时俱进的教学课堂，给教学方式改革带来一股清风是我们研究的重点。

概率论与数理统计是一门应用性很强的学科，生活中很多实际问题都可以用概率论中的方法来分析和解决。如何使学生掌握基本概念、原理、思想和方法，对概率论与数理统计的整个知识体系有所了解，并将所学在实际问题中得以创新和运用，是数学教师在教学过程中需要不断探索的问题。针对学生“学不致用”或“学难致用”问题，我们将利用网络环境，结合此次新冠疫情，发动学生利用各种网络环境收集相关数据，用概率论中的数学期望知识研究核酸检测混采分组中的人数问题。除了让学生顺利完成课堂教学安排的基本内容外，还让学生“学以致用”，能够举一反三，提高网络环境下学生自主学习概率论的能力。下面我们将具体阐述这一过程在课堂上如何实施。

首先学习数学期望的概念。数学期望是随机变量的数字特征之一，刻画了随机变量总体取值的平均水平。离散型随机变量数学期望的定义如下：

定义［1］：设离散型随机变量X的分布律为，若级数绝对收敛，则称的值为离散型随机变量X的数学期望，记作（E）X，即。

结合课本完成课堂教学安排的基本内容后，让学生在国家卫生健康委员会网站、武汉市卫生健康委员会网站、世界卫生组织网站等网络上了解新型冠状病毒肺炎疫情的波及范围、危害、诊断、预防、治疗、疫苗等相关信息，获取各地区确诊病例、人口、核酸检测等关键数据，为解决目标问题做好铺垫。

一、问题提出

自2019年12月末以来，新冠疫情在全球已具有大流行特征，传染速度快、传播广、变种多、致死率高，对社会生产和人民生活带来巨大影响。根据世界卫生组织报道，截至2021年11月2日，新型冠状病毒肺炎国外累计报告确诊病例247755167例，造成累计死亡病例5015641例；国内累计报告确诊病例126163例，累计死亡病例5696例［2］。为有效遏制疫情，核酸检测是病患预防检测及确诊检测的重要技术之一。核酸检测方法有单采和混采两种。单采就是一个人的采集拭子放到一个采集管中。混采是将若干个人的采集拭子放到一个采集管中，检测结果为阴性时，混采样本均视为阴性，代表混采的所有人都是安全的；如果出现阳性，相关部门会立即对该混采管的受试者暂时单独隔离，并重新采集单管拭子进行复核，再确定这当中到底哪一个是阳性。混采最常用的包括5合1混采和10合1混采2种。一般情况下，对于发热门诊有症状患者、密切接触者、重点区域人群等高风险人群检测，建议采用单采单检。在阳性率极低（0.1%）的情况下或进行大面积筛查则可以进行混采。而对于目前，对大面积筛查采用的是10合1混采。混采大幅提升了核酸检测能力，可使日检测能力在不增加人力物力的情况下，效率增加10倍，起到多筛查、减少传播、节约社会成本的作用，提升了新冠病毒核酸检测能力和效率，有效满足了疫情常态化防控需求。

那么，为什么是10合1混采？15合1的混采可以吗？究竟几合1的混采在理论上是最经济、高效的？检测机构在决定10合1混采时，是通过理论计算还是根据实践操作？在目前阳性率极低的情况下，可不可以把混采人数增多？根据这些提问，激发学生对新事物的探究热情，引导学生自主探索，有效地启发学生的思考，使学生成为学习的主体，为解决问题做好热身准备。

二、数学期望在核酸检测混检分组人数问题中的应用

为使研究的问题具有一般性，假定n和1的混采是有效合理的。设每组核酸检测的次数为随机变量X，若混采采样为阴性，则X=1若混采采样为阳性，则CR武汉市截至2020年4月8日解封时，累计病例为50008例［3］，按留在城里900万人口计算，个体被感染的概率为50008/900万=0.5556%，从而得到随机变量X的分布律

X 1 n+1 P （1-0.5556%）n 1-（1-0.5556%）n

按照离散型随机变量数学期望的定义可知，每组平均检测次数为

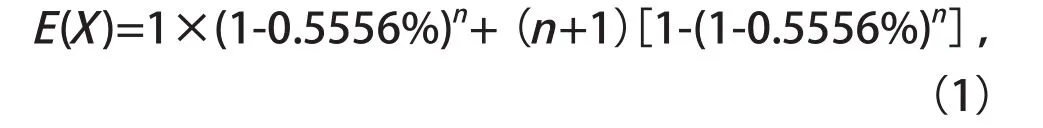
则全市900万人平均检测次数为：全市的分组数乘以每组平均检测次数，即

要使检测效率高，花费时间短，经济成本低，就是要算当每组人数n为何值时，f（n）取最小值。

通过（1）（2）式解析式的建立，学生不仅掌握了当堂课的内容，还应用所学来解决国民经济中遇到的问题，培养了分析问题解决问题的能力，锻炼了采集数据、分析数据、处理数据的技能，进一步激发学习兴趣，增强学习概率论与数理统计课程的信心。

要想求出（2）式中f（n）的最小值，学生们讨论后发现用代数的方法在理论上是可行的，但是对于实际问题来说，不能得到理想的结果，研究后决定借助Matlab或Excel软件处理大量数据的运算。概率论与数理统计课程有很多图像和大量数据运算，学生可利用Matlab软件绘制图形，通过数形结合来加深对知识点的理解；借助于Excel、SPSS等办公或统计软件处理大量数据的运算，将学生从繁琐的数字运算中解放出来，把更多的时间放在对概念和思想方法的正确理解上。通过本课程的学习，让学生掌握一些基本的统计软件，也是我们的培养目标之一。最后，学生借助Excel软件，采用枚举法算出全市平均检测次数f（n），并制表1如下：

从表1可以看出，每组中随着人数的增加，全市平均核酸检测次数呈递减趋势，当n=14时达到最小值，随后又呈递增状态，也就是说，在个体被感染概率为0.5556%的前提下，核酸检测每组14人可以使全市平均检测次数最少、花费最少、效率最高。由此学生们可以得出结论：不一定非得是10合1的混检模式，14合1的混检模式在理论上是更有效的。又注意到，（2）式中用到的个体被感染的概率为0.5556%。实际上，个体感染率应该小于0.5556%，因为在计算个体感染概率的时候，是用50008除以900万，其中50008是武汉市从疫情以来到城市解封这一时间段内的累计确诊病例，且患者一旦确诊就被隔离，所以真正同时存在于社交网络的染病者一定会远远小于50008，也就是说，0.5556%应该是高估了感染率，在此情况下，混检采样每组中的人数应该比理论算出的值14还要大。

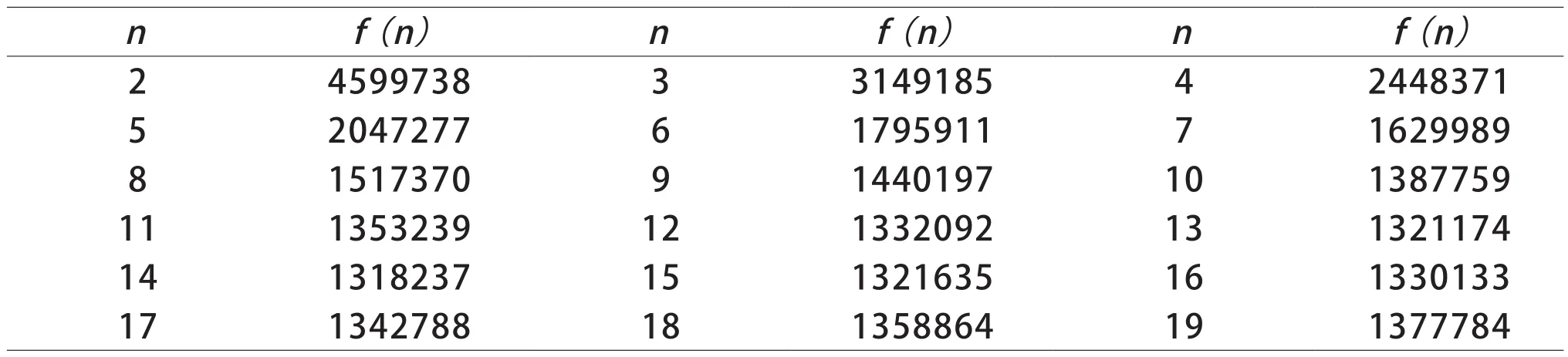
表1 武汉市平均检测次数（阳性率为0.5556%）

人们工作和生活中遇到的问题可能会有不止一种答案，但是如果不懂问题的来龙去脉和答案的确切含义，多种答案只能是学生的负担。缺乏批判性思维、创新性的学生，就会被浩如烟海般的知识所淹没。通过对核酸混检几合一问题的讨论，培养学生用批判的眼光看待遇到的一切问题，从普遍认为是真理、定论、不可更改的事实中找出不合理的因素，用理性、科学的思维和方法对待周围一切事物。

三、举一反三

进一步启发学生，如果个体被感染的概率较低，如从武汉市5月11日—5月21日对900万人的核酸检测结果知，阳性率仅为0.018%［3］，面对如此低的阳性率，10合1的混采检测需要改进吗？如果要改进，那么几合1的混采模式是更合理有效的？需要学生进一步利用网络搜集数据解决这类实际问题。与表1类同，学生们利用Excel，用枚举法罗列出了5月11日—5月21日武汉市理论上的平均检测次数f（n）。

从表2可以看出随着每组混采人数的增加，在阳性率仅为0.018%的前提下，全市平均检测次数逐渐减少，直到n=75时减到最低，随后又逐渐增加，因此从数学理论上讲，混采人数每组75人时，可以使全市平均检测次数最少。

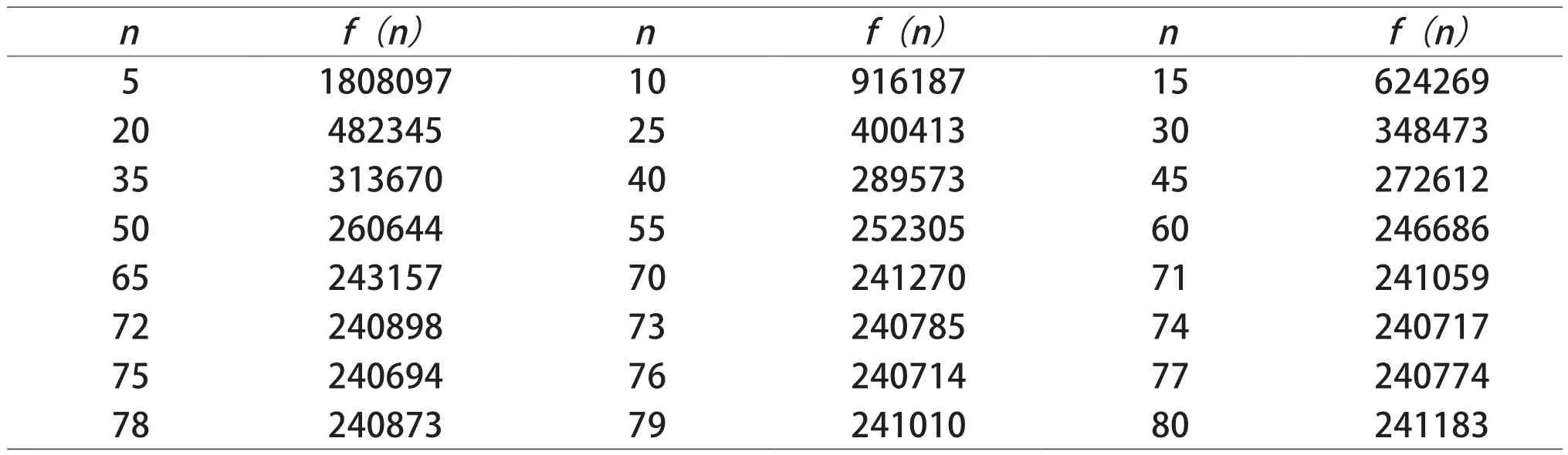
表2 武汉市平均检测次数（阳性率为0.018%）

根据其他国家的新冠疫情，核酸检测又该几合1比较合理呢？鼓励学生在网络上搜集数据解决相关问题，加深对数学期望的理解，能举一反三解决实际问题。

四、总结

在教学活动中，教师把握了教学内容的实质和学生的实际情况，创设情境、设计问题，通过恰当的提问，引导学生积极思考，激发学生的好奇心，努力营造生动活泼的课堂氛围，形成了有效的学习活动，使学生成为学习的主体，逐步学会学习。学生通过亲身参与对核酸检测分组人数问题的研究，在思考、解决问题和情感态度方面得到发展，在应用中获得知识技能，巩固了数学期望的学习，加深了对概念的理解，诠释了理论联系实际、学以致用的重要性。同时，借助网络平台，锻炼了学生自主收集信息、查找数据、灵活应用理论知识、解决实际问题的能力，也培养了学生不唯书、不唯上、遇到具体问题冷静分析、独立创新的批判精神。