按比例输入的结核病模型的动力学研究

李淑萍，刘花芳

(中北大学 理学院，太原 030051)

数千年以来，结核病对人类的健康造成了重大的危害，从近年来全球与中国关键数据可以看出[1-2]，我国的结核病情况依然很严重。为了研究结核病的传播，人们通过考虑不同的因素建立了结核病传播的各种动力学模型：

Bowong等[3]和Huo等[4]应用一般接触率分别考虑了简单的SEI模型及含有耐药菌株的SE1E2I1I2的结核病模型；考虑到治疗对结核病的作用，宋妮等[5]、Das等[6]、Saputra等[7]和Feng等[8]研究了带治疗(恢复)的SEIT (SEI R)模型；随着卡介苗的出现，Gao等[9]和李春等[10]探究了带免疫的SVEIT模型，但输入全部进入了易感者仓室。考虑到输入人群中除易感人群外，还有已经接种疫苗的人群，本文考虑了将按比例输入与不完全免疫及治疗相结合的结核病传播动力学模型[11]。对于该模型，运用稳定性理论[12]，对其无病平衡点和正平衡点的局部稳定性与全局稳定性进行分析，并应用最优控制理论得到最优控制解的存在唯一性及其表达形式；其次，通过数值模拟验证理论结果并对参数的敏感性进行分析；最后，总结本文主要的研究工作。

1 模型的建立

将总人口N(t)分为5 类，分别是：易感者S(t)，疫苗接种者V(t)，潜伏者E(t)，染病者I(t)，治疗者T(t)，显然有N(t)=S(t)+V(t)+E(t)+I(t)+T(t)。假设Λ为总人口中的输入率，q表示输入人口中进入易感者仓室的比例，其余输入人口均为疫苗接种者，a表示针对易感者的接种率，b表示被接种者免疫力的丧失率，μ表示自然死亡率，d表示因病死亡率，β表示染病者对易感者的传染率系数，k表示潜伏者到染病者的转化系数，α表示治疗率。基于以上假设，建立如图1所示的结核病传播机制。

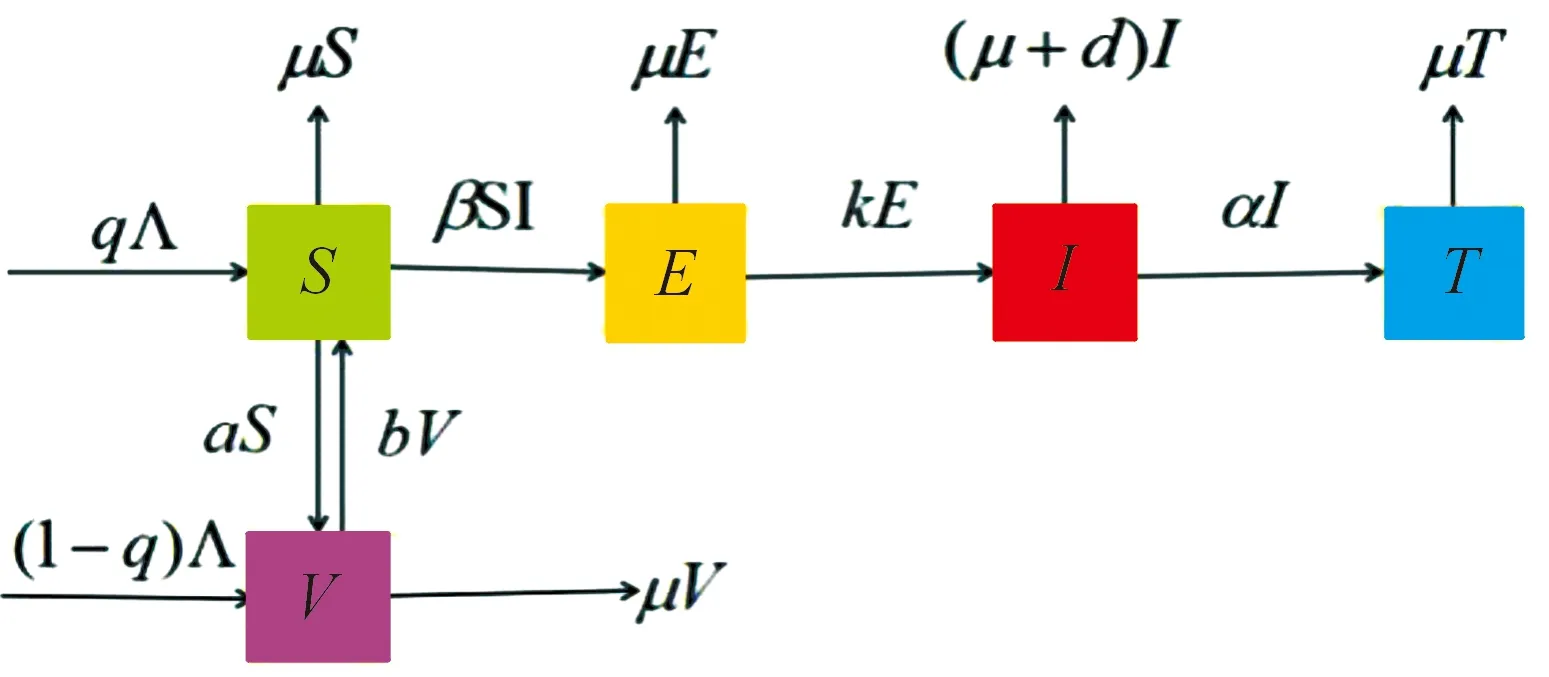
图1 结核病传播机制示意图

对应的结核病传播动力学模型为

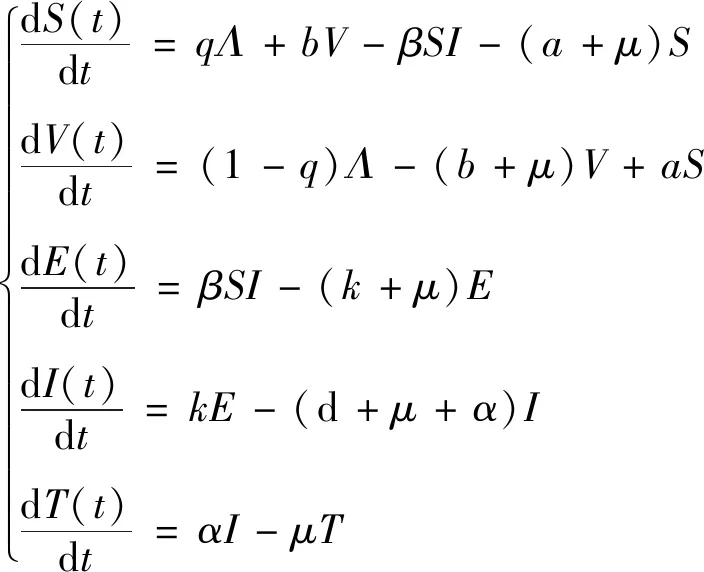
(1)

将式(1)的所有方程相加可得

(2)

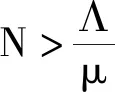
Ω={(S，V，E，I，T)|S≥0，V≥0，E≥0，

对于系统(1)，有以下结论。

命题1Ω在R5内为系统(1)的正向不变集。

证明定义函数

N(t)=S(t)+V(t)+E(t)+I(t)+T(t)

则

(3)

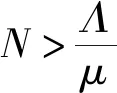
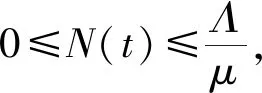
由于系统(1)的前4个方程均与T无关，故系统(1)可导出下面的等价系统

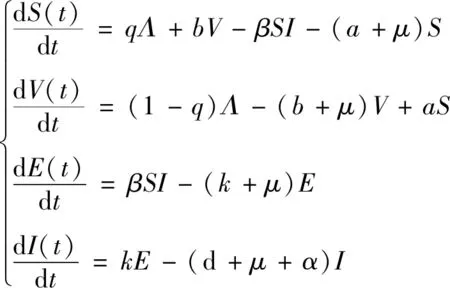
(4)

在下述讨论中只考虑等价系统(4)。

2 平衡点和基本再生数

通过简单计算可得，系统(4)的无病平衡点为P0=(S0，V0，0，0)，其中

利用下一代矩阵法[13]，可得系统(4)的基本再生数为

为了得到系统(4)的正平衡点P*=(S*，V*，E*，I*)，令

(5)

由式(5)的前2个方程可得

由式(5)的最后一个方程可得

将S*与E*的表达式代入式(5)的第3个方程可得

(6)

显然，式(6)有2个根

(ⅰ)I0=0；对应无病平衡点;

当R0>1时，系统(4)存在唯一的正平衡点P*=(S*，V*，E*，I*)，其中S*，V*，E*，I*的表达式如下

(7)

综上，有下面的定理。

定理1 当R0≤1时，系统(4)仅有一个无病平衡点P0；当R0>1时，系统(4)有两个平衡点，分别是无病平衡点P0和正平衡点P*。

3 平衡点的稳定性

3.1 无病平衡点的稳定性

定理2 当R0<1时，系统(4)的无病平衡点P0在Ω内全局渐近稳定；当R0>1时，无病平衡点不稳定。

证明为了证明P0的全局稳定性，构造如下的Lyapunov函数

V(t)=kE+(k+μ)I

它沿着系统(4)的解的导数为

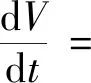
k(βSI-(k+μ)E)+

(k+μ)(kE-(d+μ+α)I)=

kβ(S-S0)I+(k+μ)·

(d+μ+α)I(R0-1)

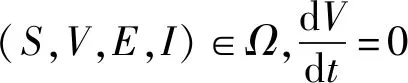
下面证明R0>1时，P0不稳定。系统(4)在P0处的Jacobian矩阵为

矩阵J(P0)的特征方程为

(8)

则

(α+k+d+2μ)2>4kβS0+(α-k+d)2

化简可得

即R0<1，与定理中R0>1矛盾，故假设错误，所以λ1>0，从而式(8)有一个正实根，因此R0>1时，无病平衡点不稳定。

3.2 正平衡点的稳定性

定理3 当R0>1时，系统(4)唯一的正平衡点P*局部渐近稳定。

证明系统(4)在P*处的Jacobian矩阵为

特征方程为

λ4+a1λ3+a2λ2+a3λ+a4=0

其中

a1=a+μ+b+μ+βI*+d+μ+α+k+μ>0

a2=(a+μ)(b+μ)+βI*(b+μ)-

ab+(d+μ+α+k+μ)(a+μ+b+μ+βI*)>0

a3=(d+μ+α+k+μ)[(a+μ)(b+μ)+

βI*(b+μ)-a*b]+

(d+μ+α)(k+μ)βI*>0

a4=(d+μ+α)(k+μ)(b+μ)βI*>0

定理4 当R0>1时，系统(4)唯一的正平衡点P*全局渐近稳定。

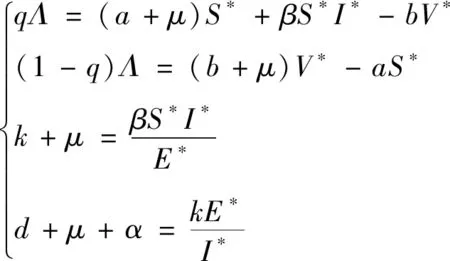
(9)

利用式(9)，系统(4)可被改写为

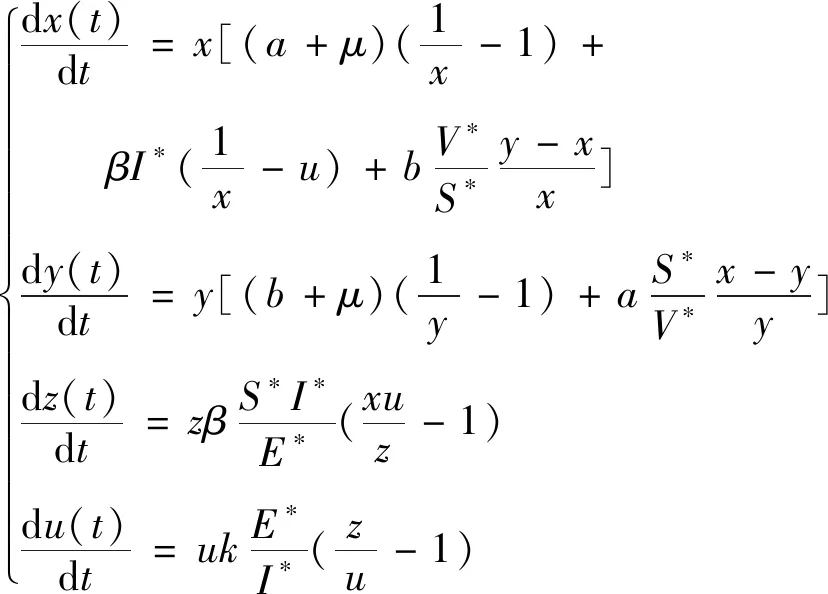
构造如下的Lyapunov函数

V(t)=S*(x-1+lnx)+

E*(z-1+lnz)+

则

F(x，y，z，u)

当bV*<(a+μ)S*时，上式可化为

F(x，y，z，u)=((a+μ)S*-bV*)·

当bV*>(a+μ)S*时，上式可化为

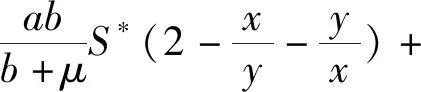
4 最优控制策略

最优控制方法有助于找到经济有效的控制各种疾病的策略，从而达到尽可能减少患病人数与相应战略成本的目的。因此，我们可以通过接种疫苗，提高治疗率及隔离等策略以不同的成本实现对结核病的控制。令X=(S，V，E，I，T)，定义U={ui|i=1，2，3}，其中u1表示可以提高个体免疫力的疫苗接种策略，u2表示可以提高染病者治疗率的控制策略，u3表示减少易感者与感染者接触的隔离策略。由于医疗技术与成本的控制，每一种控制策略ui都是有上界uimax的。具有控制策略的模型由以下非线性微分方程组给出：

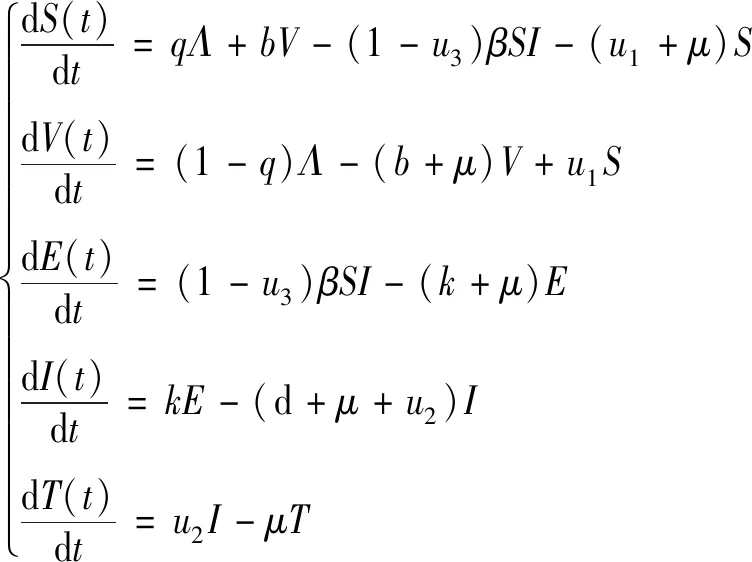
(10)

目标集X为

X={X(·)∈W1，1([0，T];R5)|满足式(1)与(10)}

控制集U为

U={U(·)∈L1([0，T];R3)|

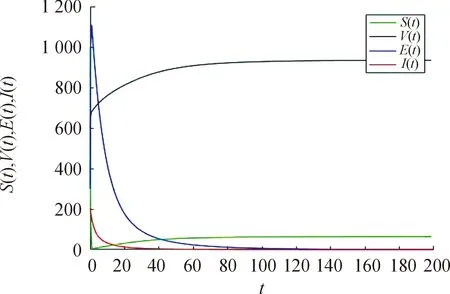
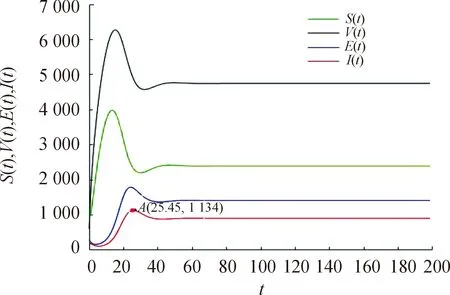
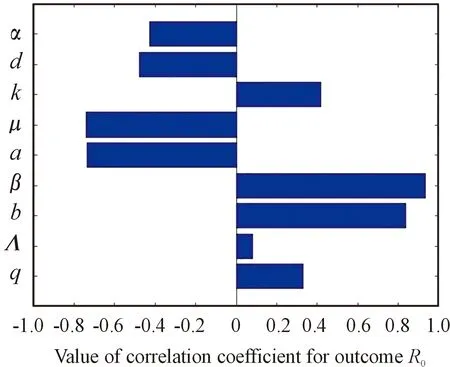
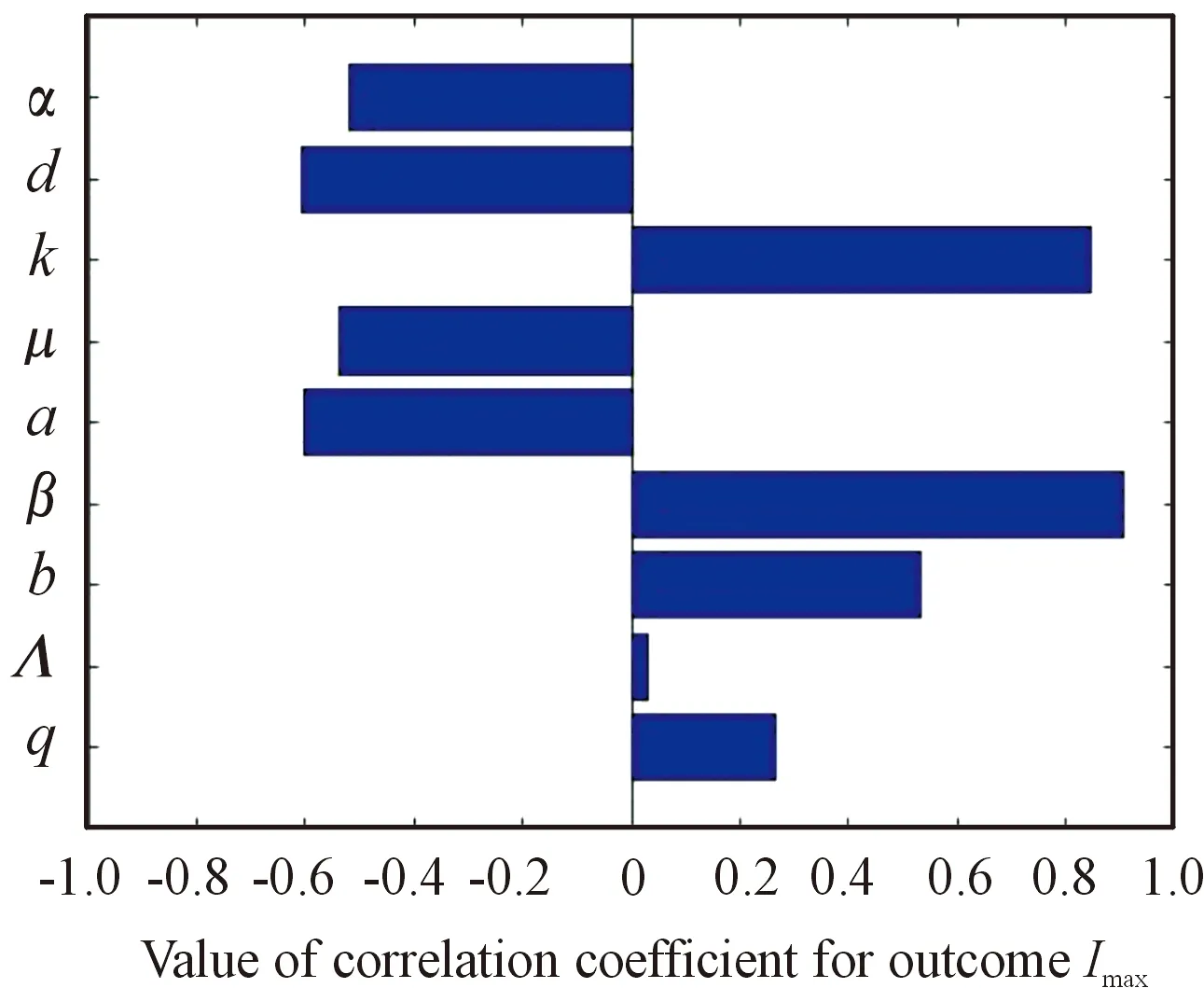
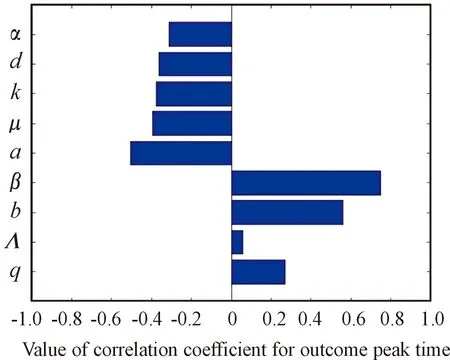
0

考虑目标函数

(11)

(12)

由文献[15-16]可得系统最优控制解的存在性，接下来根据Pontryagin最大值原理，给出最优控制解的表达形式。

若U(·)∈X为在最终固定时间T上的最优解，则存在非平凡，全连续的映射λ∶[0，T]→R5。

λ(t)=(λ1(t)，λ2(t)，λ3(t)，λ4(t)，λ5(t))

称为协态向量，即存在不为零的协态向量λ(t)，使得

① 控制方程满足

② 协态方程满足

③ 极小值条件为

H(X◇(t)，U◇(t)，λ◇(t))=

④ 极小值条件对于∀t∈[0，T]成立，构造哈密尔顿函数

λ1(qΛ+bV-(1-u3)βSI-(u1+μ)S)+

λ2((1-q)Λ-(b+μ)V+u1S)+

λ3((1-u3)βSI-(k+μ)E)+

λ4(kE-(d+μ+u2)I)+λ5(u2I-μT)

⑤ 横截条件为

λi(t)=0，i=1，…，5

由文献[15-17]可得以下定理。

定理5 如果系统(10)存在最优控制U(t)及相应的最优解(S◇(·)，V◇(·)，E◇(·)，I◇(·)，T◇(·))，则存在协态向量λi，i=1，…，5使得

横截条件为

λi(T)=0，i=1，…，5

最优控制解的表达形式为

5 数值模拟

5.1 平衡点的稳定性

在系统(4)中选取参数q=0.01，Λ=100，b=0.03，β=0.025，a=0.35，μ=0.1，k=0.032，d=0.12，α=0.3，通过计算可得R0=0.752 7<1，此时，系统(4)存在惟一的无病平衡点P0，由定理(2)可得P0是全局渐近稳定的，如图2所示。

图2 当R0<1时，P0全局渐近稳定曲线

在系统(4)中选取另外一组参数q=0.15，Λ=1 500，b=0.45，a=0.55，β=0.000 375，k=0.48，μ=0.096，d=0.002 6，α=0.65，通过计算可得R0=2.763 8>1。此时，系统(4)存在惟一的正平衡点P*，由定理可得P*是全局渐近稳定的，且在第25天(A点)时染病者数量达到峰值，如图3所示。

图3 当R0>1时，P*全局渐近稳定曲线

5.2 敏感性分析

敏感性分析常用来确定模型对参数值的稳定性。图4表明Λ对R0的影响很小，β、b、k、q均为R0的正相关变量，μ、a、d、α均为R0的负相关变量。显然，在所有变量中，β对R0的影响最大，即β是R0中更重要的因素。从图5和图6可以看出：β也是Imax与患病人数到达峰值时间的关键参数。换言之，敏感性分析告诉我们预防胜于治疗，在控制肺结核传播方面，加强预防的努力显得尤为重要。

图4 R0与参数的相关性直方图

图5 Imax与参数的相关性直方图

图6 峰值时间与参数的相关性直方图

5.3 最优控制策略

为了验证最优控制的有效性，利用前后扫描法与4阶龙格库塔公式相结合的方法对其进行了数值模拟。考虑到医疗技术与成本的因素，每种控制策略都有上限，分别取控制变量的最大值如下：u1=0.6，u2=0.8，u3=0.7。由图7可知，随着时间的增加，各种控制策略的投入可以适当地减少，从而减少成本；图8更为直接地反映了无论是R0>1还是R0<1，采取最优控制方案后，患病者的数量都急剧减少，显然最优策略的应用可以使结核病得到有效的控制。

图7 控制变量u(t)与t的函数关系

图8 施加控制前后染病者的数量

6 结论

研究了一种按比例输入的结核病模型的全局动力学行为，通过构造Lyapunov函数，利用LaSalle不变集原理的方法，研究了系统的无病平衡点和正平衡点的稳定性。当R0<1 时，无病平衡点是全局渐近稳定的，此时疾病将会逐渐消失；当R0>1时，正平衡点是全局渐近稳定的，在这种情况下，结核病将一直存在。通过对基本再生数，最高患病人数及患病人数到达峰值时间作敏感性分析得到传染率系数β是一个关键参数，对于结核病的预防及控制有重要意义。因此，在人们的日常生活中，可以通过提高个人的预防意识来降低β的数值，从而达到有效预防和控制结核病的目的。