求解高维复杂函数的两类新型蝗虫优化算法

王 倩，李风军

(宁夏大学 数学统计学院，宁夏 银川 750021)

为特定问题的变量寻找最佳值以最小化或最大化目标函数的过程称为最优化。近年来，随着越来越多群智能优化算法的提出[1-5]，用于高维复杂函数的优化算法也层出不穷[6-10]。Saremi等[11]于2017年提出蝗虫优化算法(grasshopper optimisation algorithm，GOA)，通过模拟自然界中蝗虫的成群行为来解决相关优化问题。其优势在于能够有效搜索给定空间的潜在区域，即具有较好的全局寻优能力。但随着研究的不断深入，GOA收敛速度慢，收敛精度不高的缺点逐渐暴露。针对这一问题，Ewees等[12]提出一种基于反向学习策略的GOA，通过计算当前解的反向解，增加了种群的多样性。Azar等[13]提出基于反向学习和价值函数方法的GOA，收敛精度有所提高，但没有达到最优值的情况。Jie等[14]提出基于高斯变异和Levy飞行策略的GOA，增强了搜索的随机性，从而提高了全局搜索能力。Xu等[15]引入了正交学习和混沌开发2种策略，结论表明这2种机制对于缓解不成熟收敛具有重要意义。

文献[12-15]对GOA的改进主要是通过结合某种策略以平衡探索和开发能力，尽管取得了一定效果，但是GOA的寻优性能仍具有提升的空间，值得继续探究。Arora等[16]引入了混沌映射代替线性自适应参数c，显著地提升了算法的寻优性能。李洋州等[17]提出了基于曲线自适应的蝗虫优化算法，对线性自适应参数的改进提供了新的思路。

受文献[16-17]的启发，本文将构建2种新型的蝗虫优化算法(novel grasshopper optimization algorithm，NGOA)。NGOA1的主要思想是将提出的非线性自适应参数作为当前最佳位置的权重，进而提升全局搜索能力。NGOA2是在此基础上，提出精英蝗虫位置更新策略，即选用当前最优蝗虫指导其他蝗虫的位置更新，用以加快算法的收敛速度。最后，利用NGOA1、NGOA2求解9个常用测试函数。实验结果表明：本文提出的算法具有出色的寻优性能。NGOA2对于4个单模态基准函数和2个多模态基准函数，在30次模拟中均能达到全局最优值，这在其他改进的GOA中是少见的。即NGOA2不仅能达到较高的收敛精度，且具有良好的稳健性。

1 蝗虫优化算法

蝗虫优化算法的基本思想是通过不断更新蝗虫位置，最终达到全局最优值或接近全局最优值的近似解。对应的蝗虫位置向量即为函数的自变量，并假定影响蝗虫位置Xi更新的因素包括其他蝗虫的社会作用力Si、该蝗虫受到的重力Gi和风力Ai。用来模拟蝗虫成群行为的数学模型如下：

Xi=Si+Gi+Ai

(1)

其中Si，Gi，Ai的表达式分别为：

(2)

(3)

(4)

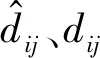
(5)

(6)

dij=|xj-xi|

(7)

其中:f表示吸引力的强度；l表示吸引力的长度。GOA算法中取f=0.5和l=1.5。

将Si，Gi，Ai代入式(1)，则有

(8)

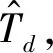
(9)

(10)

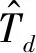
2 两类新型蝗虫优化算法

2.1 非线性自适应参数及NGOA1

GOA在位置更新公式中采用线性递减参数，不利于算法有效地进行全局搜索和局部搜索，从而使得算法的收敛精度不高。为改善GOA的寻优性能，文献[17]提出了圆弧自适应参数，表达式如下：

(11)

圆弧自适应参数在迭代前期递减速度较慢，使得算法在离最优值较远处停留时间过长，进而影响算法整体的收敛速度；在迭代后期递减速度较快，不利于算法充分地进行局部搜索，因此可能会导致算法收敛精度不高。针对以上问题，本文构造出非线性自适应参数，旨在通过改进线性自适应递减参数，提升蝗虫优化算法的寻优性能，表达式如下：

(12)

线性自适应参数、圆弧自适应参数及非线性自适应参数随迭代次数变化的趋势如图1。

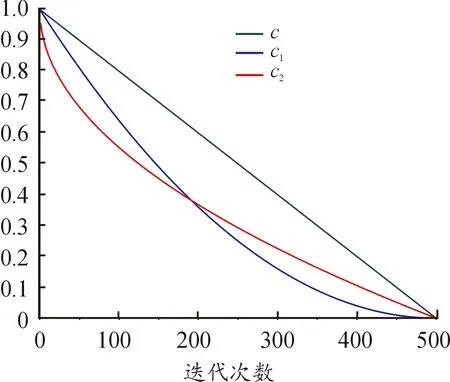
图1 3种自适应参数曲线

由图1可以看出：与线性自适应参数相比，非线性自适应参数在每次迭代中的值均低于线性自适应参数值，加快了整个种群趋于最优值的速度。与圆弧自适应参数相比，非线性自适应参数在迭代前期递减更快，使得算法不容易陷入局部最优，在迭代后期递减较慢，使得算法能够细致地进行局部搜索。因此，非线性自适应参数可以更好地平衡算法的探索与开发能力，使算法更有可能获得接近全局最优值的近似解。

利用非线性自适应参数替换GOA的线性自适应参数，并将非线性自适应参数作为当前最佳位置的权重，构建第一类新型蝗虫优化算法(NGOA1)，位置更新公式如下：

(13)

2.2 精英蝗虫位置更新策略及NGOA2

GOA算法通过社会作用力函数表明，蝗虫的位置更新与其他所有蝗虫的位置均相关。但在实际应用，位置不好的蝗虫可能使得当前解更新后变差，而且对于高维复杂函数来说，计算量过大，会导致算法寻优速度极慢。鉴于此，本文提出精英蝗虫位置更新策略，即仅由当前最优蝗虫指导其他蝗虫的位置更新，使所有蝗虫均向最佳位置不断靠拢，进而加快了算法的收敛速度，也有利于提高算法的收敛精度。

将位置更新公式中其他蝗虫位置替换为当前最优蝗虫位置，提出基于非线性自适应参数和精英蝗虫位置更新策略的第二类新型蝗虫优化算法(NGOA2)，位置更新公式如下：

(14)

2.3 NGOA的实施步骤及流程图

NGOA1和NGOA2的差异表现在位置更新公式的不同，因此同时给出两类算法的实施步骤，相应的流程如图2所示。

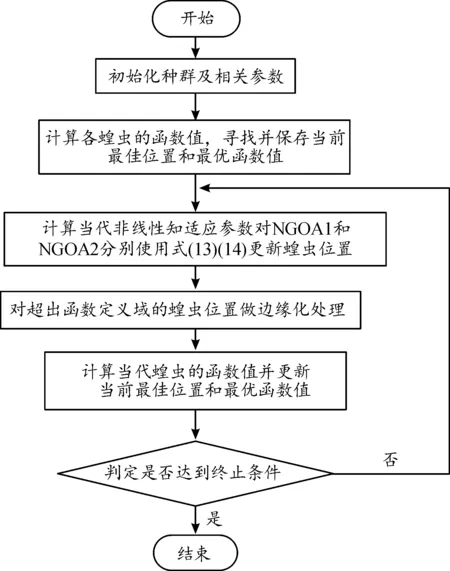
图2 NGOA的实施流程

1)设定种群规模N、最大迭代次数L、非线性自适应参数c2的上界与下界；

3)开始迭代：计算当代非线性自适应参数c2，NGOA1根据式(13)进行位置的更新，NGOA2根据式(14)进行位置的更新，得到当代的蝗虫位置；

6)若达到最大迭代次数或全局最优解，结束循环并返回最优函数值；否则，转入步骤3)。

3 实验结果与分析

为验证NGOA求解高维复杂函数的有效性，将CAGOA、NGOA1与GOA比较，探究圆弧自适应参数、非线性自适应参数的引入是否能改善GOA的寻优性能；将NGOA1与CAGOA比较，观察非线性自适应参数的作用是否优于圆弧自适应参数；将NGOA2与NGOA1比较，分析精英蝗虫位置更新策略能否提升算法的收敛精度。需要说明的是CAGOA的位置更新公式如下：

(15)

本文在Matlab R2018b的环境下进行上述实验，并对比4种算法求解9个常用的标准测试函数[1-5，11]的结果。各函数的基本信息如表1所示，F1到F6为单模态测试函数，F7到F9为多模态测试函数。设置种群规模为30，最大迭代次数为500。

表1 测试函数的基本信息

为消除初始化种群带来的影响，分别运用GOA、CAGOA、NGOA1、NGOA2算法对9个测试函数求解30次，4种算法对应的各函数最优值的收敛情况如图3所示。

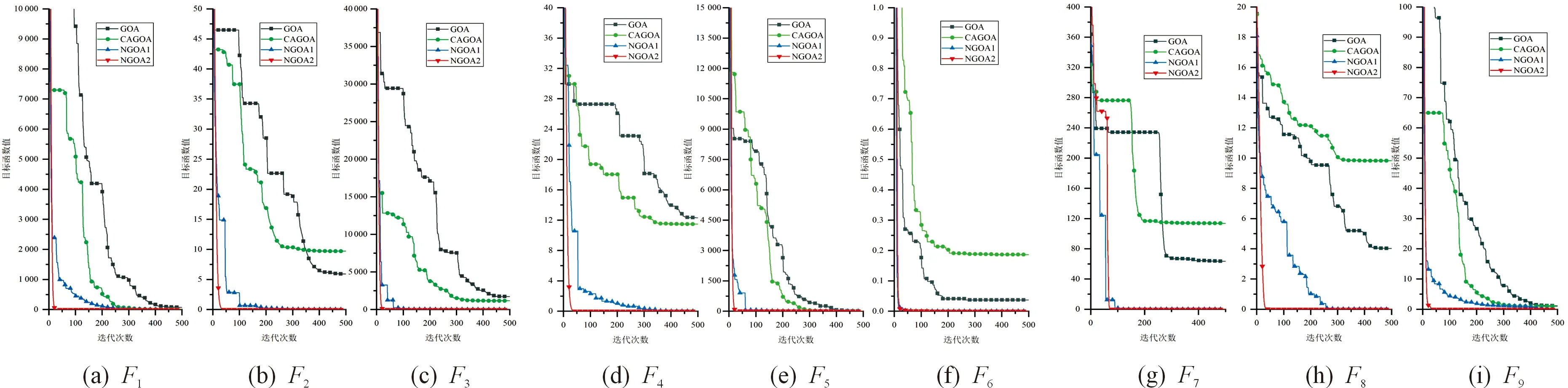
图3 GOA、CAGOA、NGOA1及NGOA2算法的收敛曲线

首先讨论CAGOA的寻优性能：对于F1～F3，F5，F7，F9来说，CAGOA的收敛精度和收敛速度略优于GOA。对于F4，F6来说，CAGOA的收敛精度和收敛速度逊色于GOA。对于F8来说，CAGOA在迭代中期略优于GOA，但是迭代后期陷入局部最优值，最后得到高于GOA的近似值。整体来看，CAGOA中的圆弧自适应参数没有使得GOA的寻优性能显著提高。

其次分析NGOA1的寻优性能：对于所有的9个函数来说，无论是单模态基准函数，还是多模态基准函数，NGOA1的收敛速度和收敛精度均远远高于CAGOA和GOA，具有较理想的寻优性能，达到了改进线性自适应参数的目的。

最后探究NGOA2的寻优性能：NGOA2求解函数F1～F9均能在迭代50次前达到较为满意的收敛精度，表明其具有较快的收敛速度。与NGOA1相比，NGOA2的收敛速度更快，收敛精度更高，表明减少非当前最佳蝗虫位置对于各个蝗虫位置更新的指导不仅不会造成算法收敛精度的降低，而且可以指导整个种群以更快的速度达到全局最优值或全局最优值的理想的近似解。

计算4种算法30次求解函数的最小值(最优值)、最大值(最差值)、平均值以及标准差，利用SPSS 26.0对求解结果进行Kruskal Wallis检验，多重比较选择Bonferroni方法，如表2、3所示。

表2 单模态基准函数的寻优结果

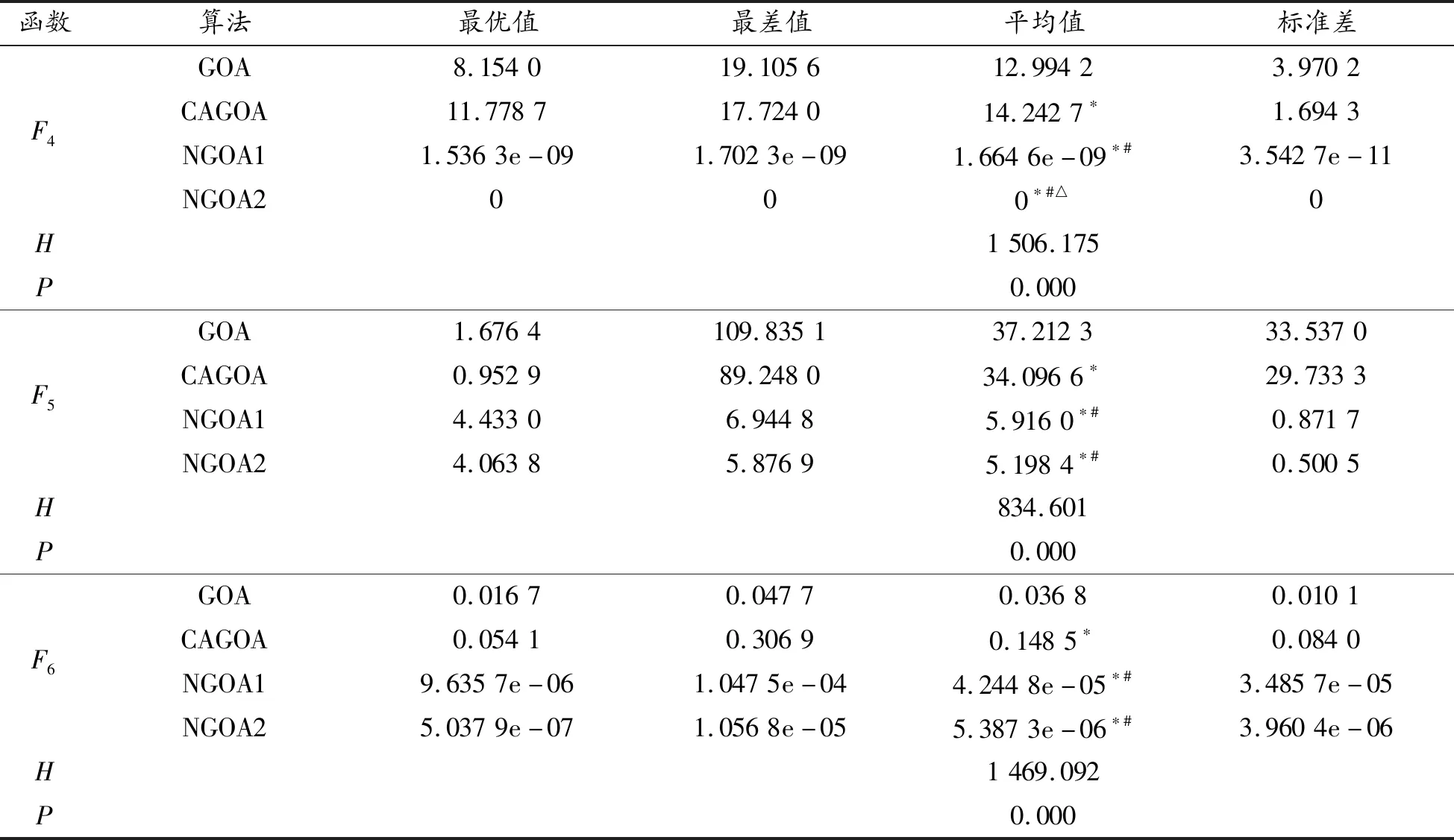
续表(表2)

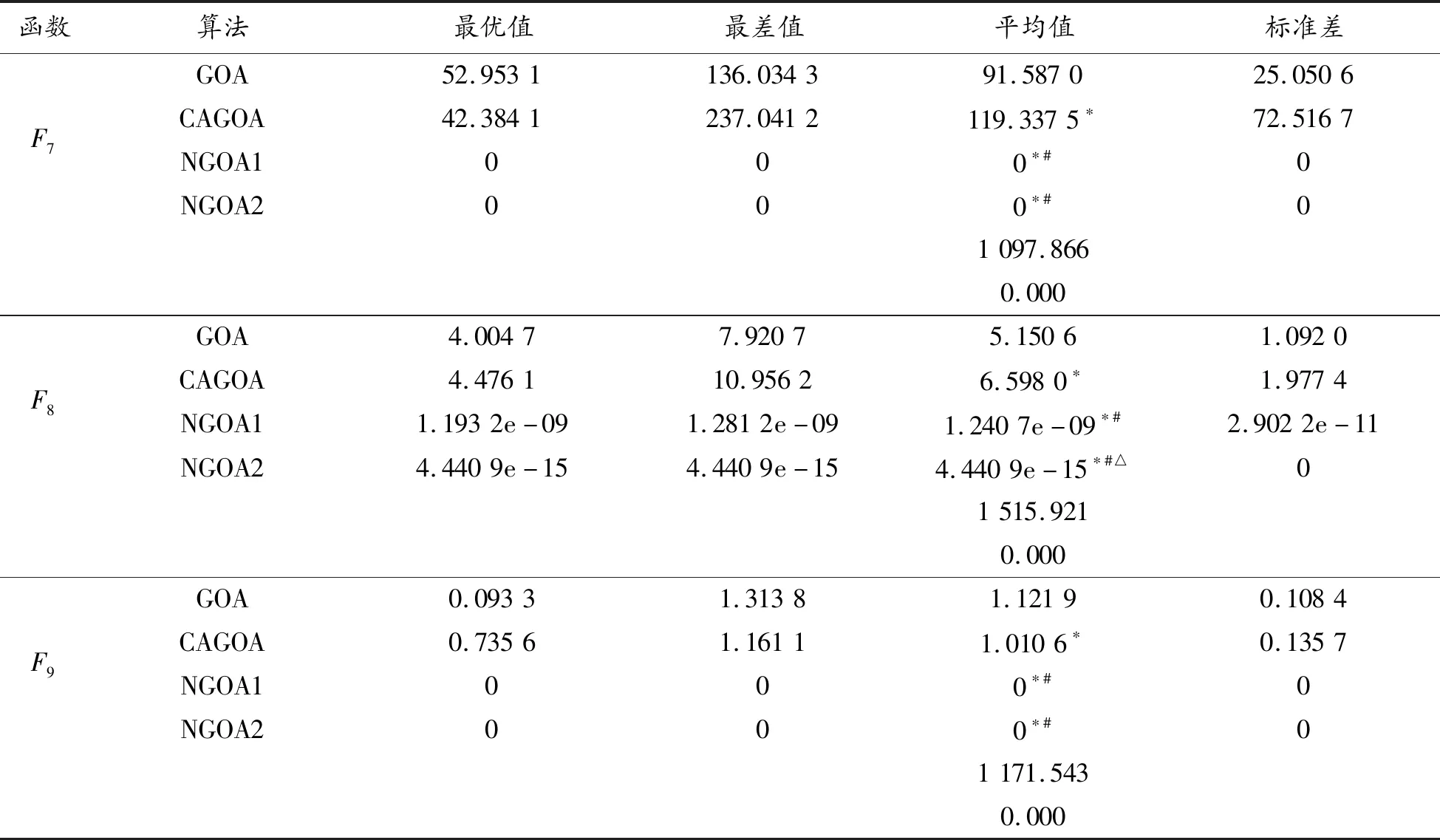
表3 多模态基准函数的寻优结果

由表2、3可以看出：CAGOA和GOA求解不同的高维复杂函数得到的最优值、最差值、平均值、标准差有优有劣，2种算法的寻优性能不分上下，进一步证明了圆弧自适应参数具有改善的空间。

NGOA1求解9个测试函数的结果均显著优于CAGOA和GOA，且具有极小的标准差，证明其具有较好的稳健性，即寻优性能好不是偶然情况。NGOA1对于单模态基准函数的求解没有达到全局最优值的情况，但于多模态基准函数F7和F8，却可以达到全局最优值。从最优值、最差值、平均值和标准差可以看出：在30次模拟中，每次均能达到全局最优值，表明其具有较好的收敛精度，且能在某些高维复杂函数寻优中跳出局部极值。NGOA2对于F1～F4、F7和F8均能达到全局最优值，彰显了求解高维复杂函数的优越性。

4 结论

1)为提升蝗虫优化算法的收敛精度和收敛速度，通过构造两类新型蝗虫优化算法NGOA1和NGOA2。

2)证明了非线性自适应参数对于蝗虫优化算法的适用性，及NGOA1对于求解高维复杂函数的有效性。

3)验证了减少非当前最佳位置指导种群中其他蝗虫位置更新是可行的。仅由当前最佳蝗虫位置决定其他蝗虫位置更新，有利于提高算法的寻优性能。

4)提出的基于非线性权重和最佳位置更新策略的蝗虫优化算法在多个单模态基准函数和多模态基准函数的30次求解中均能达到全局最优值，具有良好的稳健性，表明NGOA2具有较好的全局搜索能力，求解高维复杂函数能达到理想的收敛精度。