土工格栅加筋粗粒土的加筋影响带研究
胡幼常 田树林
(武汉理工大学交通与物流工程学院 武汉 430063)
0 引 言
土工格栅加筋粗粒土力学特性优良,加筋效果显著[1-2].筋层间距小于某一临界值的土工格栅加筋粗粒土可以形成类似于复合材料的加筋土复合体,其承载能力高、韧性好、抗变形能力强,抗震性能尤为突出[3-5].因而在工程中具有广阔的应用前景,特别适宜于用来建造或支挡高陡边坡、修建柔性桥台或桥墩.然而,什么条件下可以形成筋-土复合体呢目前还没有明确的答案.这直接阻碍了土工格栅加筋粗粒土结构在工程中的推广应用.包承纲[6]提出的“间接影响带”理论,该理论认为,土中的加筋材料不仅会在土与筋材的接触面上产生直接加筋作用,而且也会在接触面以外的一定范围内对土体产生一种间接加固作用,并称该范围为“间接影响带”.在“间接影响带”内,由于筋材带动土粒发生位移或颗粒产生破碎,土体的抗剪强度因而增大.为了与加筋土这个研究主体直接联系起来,也可将“间接影响带”称为“加筋影响带”[7].
包承纲的这一理论要用于指导工程实践,必须解决以下两个问题:①如何定量确定加筋影响带的厚度;②加筋影响带内土体抗剪强度增长量的大小及其分布规律.丁金华等[8]采用大型叠环式拉拔仪完成了单向土工格栅在膨胀土中的拉拔试验,验证了加筋影响带的存在, 并得出50,100,200和300 kPa法向压力下,加筋影响范围均在30 cm左右的结论.张嘎等[9]采用平均粒径d50为7 mm的粗粒土,在大型直剪仪上完成了土工布与粗粒土间的接触面剪切试验,观测到界面影响带的厚度约为土粒平均粒径d50的5~6倍.文献[7]完成了土工格栅在不同级配粗粒土中的拉拔试验,初步得到了加筋影响带厚度与土的平均粒径d50的统计关系,并基于此提出了加筋土坡稳定性分析的“影响带法”.该法近似认为影响带内土体的黏聚力增长了▽c,其大小与筋材的抗拉强度和筋层间距有关,而内摩擦角不变.蔡春等[10-11]分别采用拉拔试验就土工格栅横肋厚度对加筋效果的影响进行了研究,结果均表明横肋厚度增大时,土工格栅对周围土体的嵌固咬合作用随之增强.上述研究成果填补了相关研究的空白,但考虑的影响因素较少,不够全面.实际上,筋材的结构和种类、土粒大小和级配、筋-土界面法向压力等对影响带的厚度及影响带内土体的抗剪强度增长规律都可能有影响.
基于此,文中选定一种双向土工格栅,制作出具有3种不同横肋厚度的筋材试样,分别在6种不同级配的粗粒土中,完成了不同法向压力下的多组拉拔试验.拉拔仪是为研究加筋影响带而专门设计的,其拉拔盒的一个侧壁为透明的玻璃,以便于在拉拔过程中观测土粒的位移,从而分析出不同试验工况下的加筋影响带厚度.通过对试验结果的分析,得到了加筋影响带厚度与土粒平均粒径d50、不均匀系数Cu、曲率系数Cc和土工格栅横肋厚度t的定量关系式.与已有的研究成果相比,该公式较全面地考虑了粗粒土的级配对影响带厚度的影响,还定量考虑了土工格栅横肋厚度的影响.同时,考虑到筋材对土体的间接加固作用必然存在如下规律,即在筋-土界面处最强,而随着离筋-土界面距离Y的增大而逐渐减弱,本文还对不同加筋间距下,加筋影响带内土体抗剪强度增长的量值随Y值的变化规律进行了分析,确定了其分布图形.在此基础上,对文献[7]提出的加筋土坡稳定性分析方法——“影响带法”进行了改进.通过对工程实例的比较分析,讨论了 “改进影响带法”的合理性.
1 加筋影响带观测试验
1.1 试验设备及观测方法简介
用于观测土工格栅加筋粗粒土加筋影响带的试验仪器为一台定制的土工合成材料拉拔仪.其中的拉拔盒是笔者为观测加筋影响带而专门设计的(见图1).
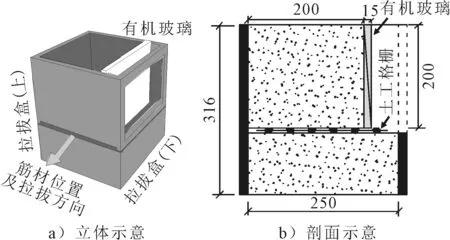
图1 拉拔盒构造示意图
为了更清晰地显示土粒的位移情况,参照文献[7]的方法,用包裹于导线皮内的大头针尖作为位移观测点,分4列(编号为L1~L4)紧贴拉拔盒的有机玻璃内壁埋设,见图2.拉拔过程中实时观测这些位移观测点的坐标变化,从而获得其位移轨迹,据此判断加筋影响带的范围.

图2 位移观测点的排列
1.2 试验材料与试验方案
加筋影响带的厚度必定与土粒的大小及级配,土工格栅横肋的厚度有关,还可能与筋-土界面上的法向压力大小有关.为此,采用3种横肋厚度的土工格栅,6种不同粒径级配的粗粒土,分别在不同法向压力下进行拉拔试验.观测各试验工况下筋-土界面及以上土粒的移动规律,进而确定每一种工况下的加筋影响带厚度,分析其与土工格栅横肋厚度、土粒级配和法向压力间的关系.
试验所用土工格栅为聚丙烯双向土工格栅,网孔尺寸30 mm×30 mm,横肋厚度t=2.58 mm,其横向及纵向破坏拉伸强度分别为53.86,51.17 kN/m.为了探究不同横肋厚度下土工格栅加筋粗粒土加筋影响带厚度的变化,分别采用单层、双层和三层格栅试样实施拉拔试验.其中,双层和三层格栅试样是采用与单层格栅试样完全相同的两层或三层格栅对齐紧密粘合而成的.单层格栅横肋厚度2.58 mm,双层和三层的分别为5.16和7.74 mm.
为探讨土粒粗细和级配对加筋影响带厚度的影响,共设计两个系列的粗粒土作为试验用土.一个系列为匀粒土,共3种,分别记为S1,S2和S3,其粒径分布范围依次为:0.6~1.18,1.18~2.36,2.36~4.75 mm.设计3种匀粒土的主要目的是为了研究土粒粗细对加筋影响带厚度的影响规律.另一个系列为非匀粒土,也有3种,分别记为S4,S5,S6,级配曲线见图3.设计3种非匀粒土的主要目的是研究土粒粗细搭配情况对加筋影响带厚度的影响.上述所有土样的级配特征指标见表1.
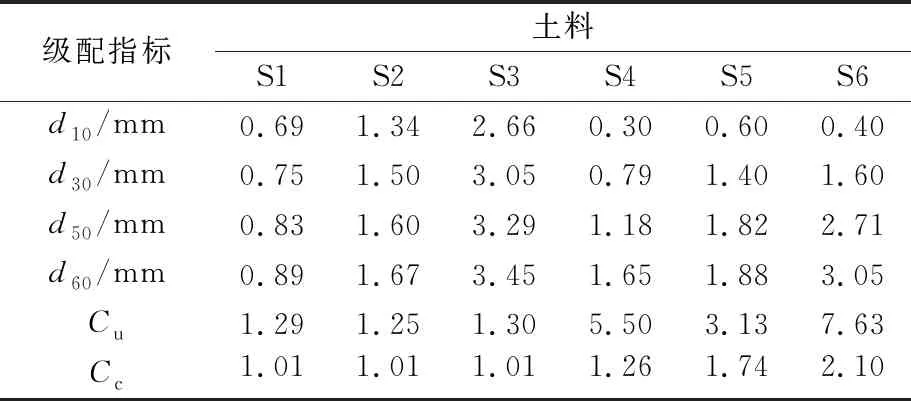
表1 各土样的土粒级配特征指标
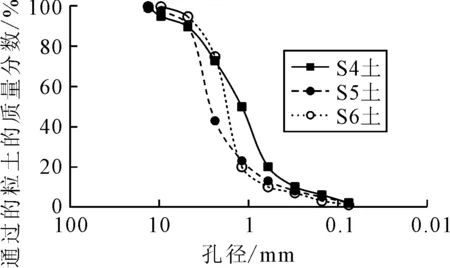
图3 非匀粒土级配曲线
为了研究法向压力对加筋影响带厚度的影响,共设计了5种大小的法向压力,分别为0,10,25,40和75 kPa.由于在75 kPa下,单层土工格栅因抗拉强度不够而拉断,所以只取前4级压力下的试验成果.
以格栅横肋厚度、土粒大小和级配、试样法向压力为变量,组合设计的拔试验方案见表2.各试验方案中,土样的压实度为85%,且均为风干土,风干含水率为0.64%.

表2 拉拔试验方案
1.3 试验结果及分析
在拉拔试验过程中,埋设于土中的位移观测点会随着格栅的带动而移动.作为代表,图4为40 kPa法向压力下横肋厚度为2.58 mm的格栅在S6粗粒土中进行拉拔试验时不同高度处的土粒横向位移情况.图中纵坐标Y为距格栅所在平面的高度,横坐标X为土粒的横向位移.由图4可知,出距离格栅表面近(即Y值小)的观测点,横向位移较大,随着Y值的增加,测点的横向位移逐渐减小.这也说明土工格栅对土体的间接加固作用是随离筋-土界面距离的增加而逐渐减弱的,直至消失.如果将间接加固作用消失处的纵坐标记为Y0,则Y0值即为单侧加筋影响带的厚度δ.根据文献[7]的观点,可以近似认为土粒横向位移为零处即为间接加固作用消失处.这样,由某一列观测点的横向位移量X拟合得出该列土颗粒横向位移值随高度Y的变化曲线,其在纵轴上的截距即为由此列观测点得到的单侧加筋影响带的厚度δi.每个试样中共埋设了四列观测点(见图2),以四列观测点得到的影响带厚度平均值作为该试验条件下的单侧加筋影响带厚度δ.
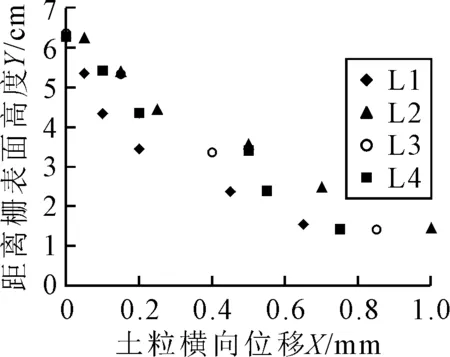
图4 典型土粒横向位移分布图
按照上述方法得到各试验工况下的单侧加筋影响带厚度δ值见表3.由表3可知:法向压力σ对加筋影响带厚度的影响较小.因此,忽略法向压力对加筋影响带厚度的影响,将相同试样在不同法向压力下得到的影响带厚度平均值作为该工况下粗粒土的单侧加筋影响带厚度 .
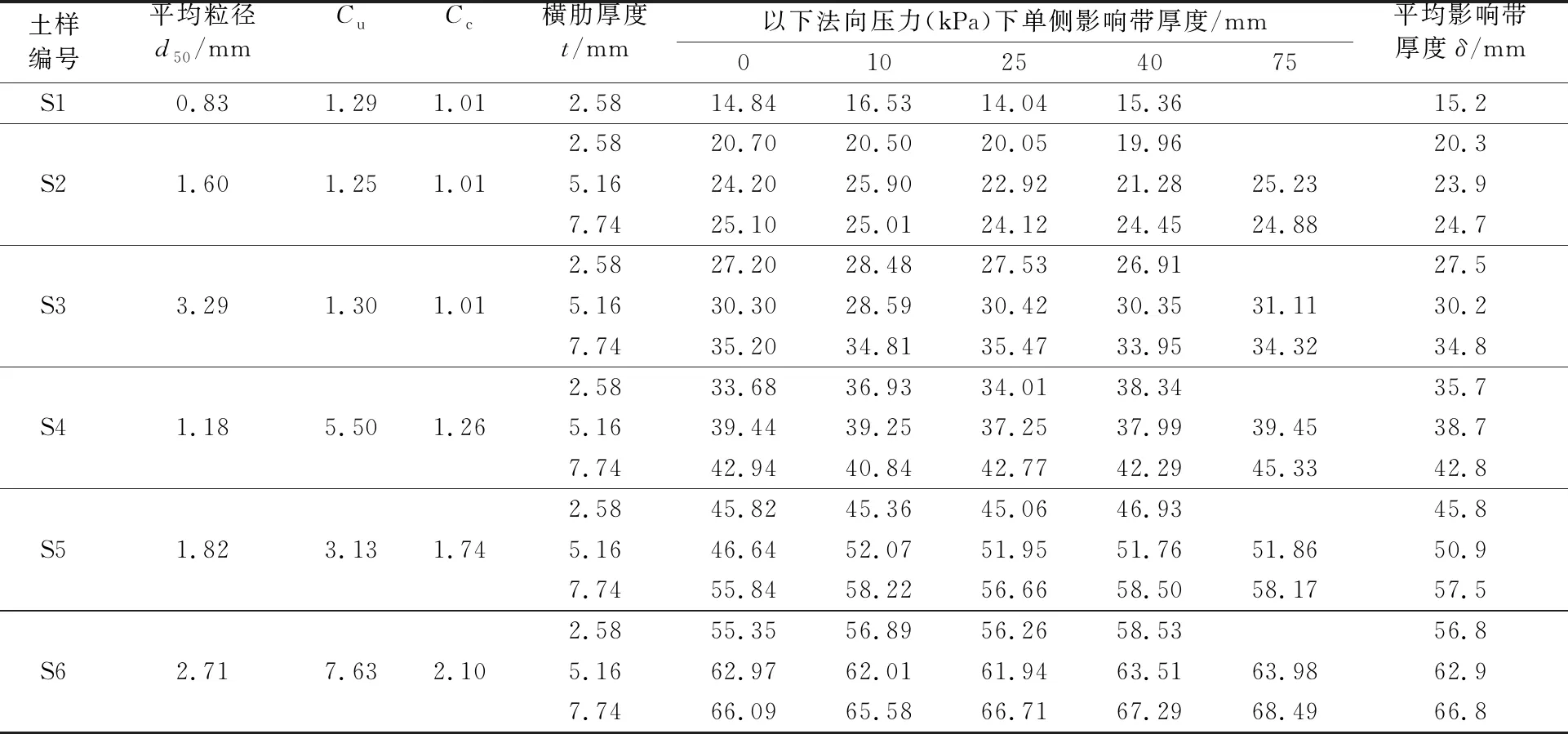
表3 不同工况下的单侧加筋影响带厚度
由表3可知:①不同工况下的平均加筋影响带厚度都随格栅横肋厚度的增大而增大;②对于3种匀粒土,其曲率系数Cc相同,都为1.01,不均匀系数Cu相近,相同格栅横肋厚度时的平均加筋影响带厚度随平均粒径d50的增大而增大;③对于3种非匀粒土,其曲率系数Cc互不相同,不均匀系数Cu相差较大,但相同格栅横肋厚度时的平均加筋影响带厚度也随平均粒径d50的增大而增大;④将匀粒土和非匀粒土的情况进行对比,则发现即使两者的平均粒径d50相近,但相同横肋厚度时的加筋影响带厚度却相差甚远.例如非匀粒土S5的d50为1.82 mm,匀粒土S2的d50为1.60 mm,两者很接近,但前者单层格栅试样的加筋影响带厚度达到了45.8 mm,而后者为20.3 mm,不足前者的一半.这说明,如果仅以平均粒径d50来反映土粒级配对加筋影响带厚度的影响是不够的,还应将其他能够反映土粒级配的指标纳入其中.考虑到不均匀系数Cu的大小能反映土粒粒径大小的分布范围,曲率系数Cc的大小能反映级配曲线的形状(即粗细颗粒的搭配情况),而土粒平均粒径d50反映了土粒的平均粗细程度,如果同时采用这三个指标来反映土粒粗细程度和粒径搭配情况对加筋影响带的影响,则比较全面.
采用多变量拟合方法,得到土工格栅加筋粗粒土的单侧加影响带厚度δ与格栅横肋厚度t、土粒平均粒径d50、不均匀系数Cu和曲率系数Cc之间的回归关系式见式(1).由式(1)算出的δ拟合值和实测值的比较见表5,二者比较接近.
(1)
式中:δ、d50、t,mm.
2 加筋影响带内土体抗剪强度增长量的分布规律
根据“间接加固作用”理论,加筋影响带内土体的抗剪强度会因筋材的加筋作用而提高.文献[7]借鉴关于加筋相当于增加了土体围压的观点,假设筋材所起的作用相当于对加筋影响带范围的土体施加了围压,亦即使影响带内土的黏聚力增加了,而内摩擦角不变.则Δc可按下述方法确定.
设一层筋材上下两侧加筋影响带厚度都为δ,则其和为2δ.并假设加筋土体中的筋材有足够的锚固长度,所以筋材的破坏型式为拉断破坏,而不会发生拔出破坏,则加筋土体达到其极限平衡状态时,筋材达到其设计抗拉强度Ta.因此,影响带内土体围压增加值Δσ3为
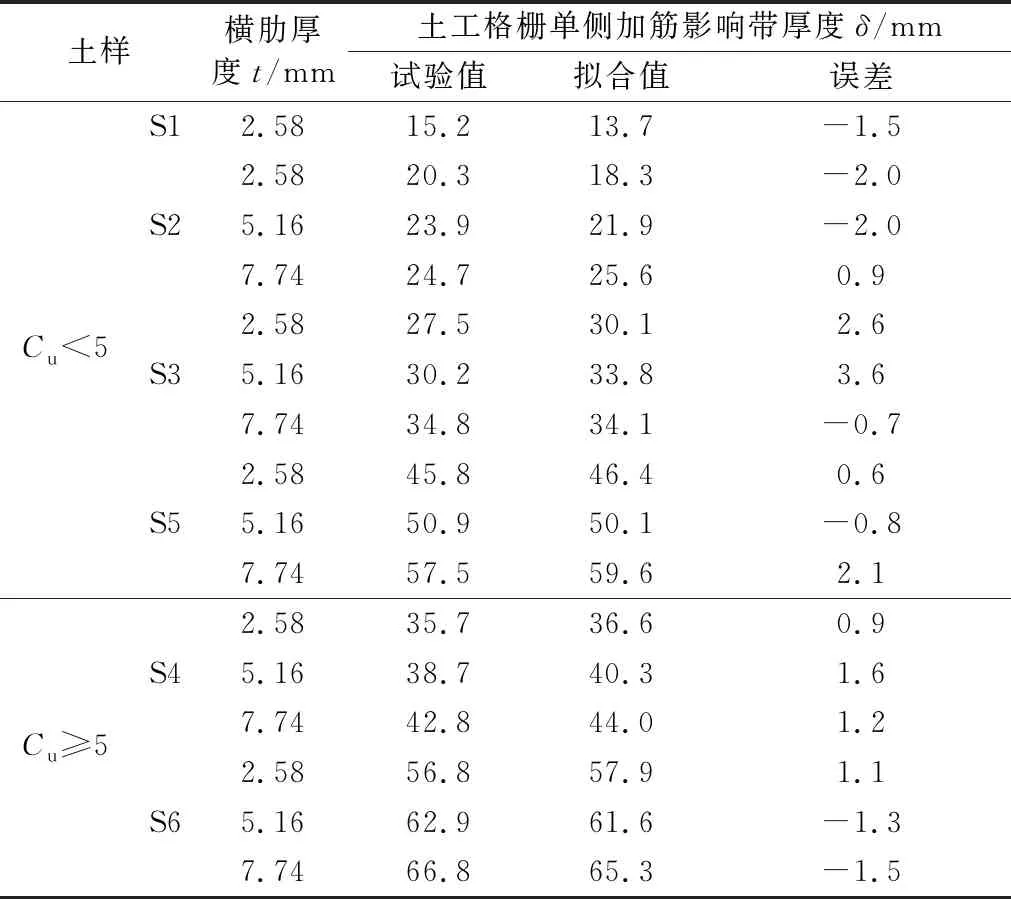
表4 δ拟合值与实测值对照表
(2)
依据加筋影响带内土体的极限平衡条件,有
σ1=(σ3+Δσ3)tan2(45°+φ/2)+
2ctan(45°+φ/2)=
σ3tan2(45°+φ/2)+2(c+Δc)tan(45°+φ/2)
其中:
(3)
将式(2)代入(3)得
(4)
文献[7]近似认为加筋影响带内土体的抗剪强度都增长了Δc,即影响带内的抗剪强度增长量沿高度方向是均匀分布的,这显然与实际情况不尽相符.如前所述,筋材对周围土体的间接加固作用是随距筋-土界面垂直距离Y的增加而逐渐减弱的.由图4可知,土粒横向位移X随Y值的增大而近似呈线性减小的规律,假定影响带内土的抗剪强度增长量也是随Y值的增大而线性下降的.这样,式(4)所确定的Δc值为加筋影响带内抗剪强度增长量的平均值,在Y=0(即筋-土界面上),抗剪强度增量最大,记为Δcmax,则Δcmax=2Δc,在Y=δ(即影响带边缘),抗剪强度增量为0.于是,当加筋层间距S>2δ时,影响带内土体抗剪强度增长量Δτf沿高度Y的分布图见图5a).
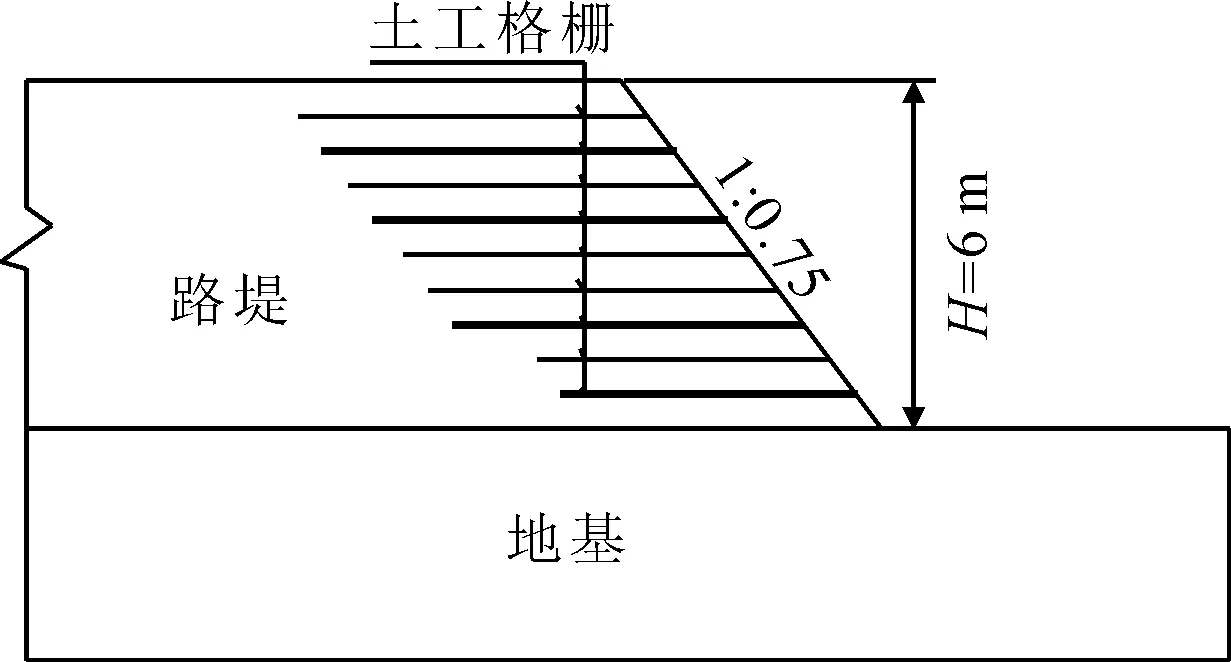
当δ Δτf1=2Δc(2-S/δ) (5) 当S≤δ时,见图5c),相邻两层筋材的加筋影响带在高度方向全部重叠,重叠区域为图5c)中阴影部分.考察相邻两层筋材间的土体,上层筋材引起的抗剪强度增长量沿高度呈倒三角形(S=δ时)或倒梯形(S<δ时)分布,下层筋材引起的抗剪强度增长量沿高度呈正三角形(S=δ时)或正梯形(S<δ时)分布,两者叠加后,其抗剪强度增长量沿高度不变,记为2Δc′,见图7.Δc′的值可按以下方法确定. 图5 Δτf-Y分布图 S≤δ时,假设每层筋材所起的作用相当于对其上、下各S厚度的土体施加了围压Δσ3.这相当于假定任意一层筋材引起周围土体抗剪强度增长的范围仅限于其上、下相邻两层筋材之间,不会跨过相邻筋材而对以外的土体施加影响.也可以理解为任一层筋材只“负担”其上、下相邻两层筋材之间土体的加固任务.故有: (6) 与式(4)的推导同理,可得Δc′的计算公式为 (7) 按照上节所述的方法,即可将筋材的加筋作用转化为一定范围内土体的黏聚力增长,将加筋土结构转换为无加筋材料的纯土结构(但处于加筋影响带内的土体抗剪强度有增加),进而分析其稳定性.这样,既考虑了筋-土的相互作用机理,又使分析方法得到简化.这种方法首先由文献[7]提出,并称之为“影响带法”.但如前所述,文献[7]假定加筋影响带内土体抗剪强度增长量沿高度不变,与实际情况不完全相符,所以本文提出了如上所述的改进.下面基于此种改进,对土工格栅加筋粗粒土坡的稳定性进行分析,并称此加筋土坡稳定性分析方法为“改进影响带法” 某实际工程中的一段加筋路堤边坡见图6,边坡高度为6 m,边坡坡率为1:0.75.共9层土工格栅,层间距S=60 cm.上部7层格栅长度都为6 m,底部2层为5 m.路堤采用卵石土填筑,其黏聚力c=4.2 kPa,重度γ=21.4 kN/m3,内摩擦角φ=39.4°,弹性模量E=60 MPa,泊松比μ=0.32,土粒的平均粒径d50=19.6 mm,不均匀系数Cu=8.30,曲率系数Cc=2.19.地基土的黏聚力c=16.7 kPa,重度γ=22.3 kN/m3,内摩擦角φ=44.8°,弹性模量E=100 MPa,泊松比μ=0.30.采用极限抗拉强度为40 kN/m的HDPE单向土工格栅,其横肋厚度为1.38 mm.参照公路规范[12],考虑筋材的蠕变、老化及施工损伤等因素,取强度折减系数为4.0,所以土工格栅的设计抗拉强度Ta=10 kN/m.现采用“改进影响带法”计算该边坡的稳定安全系数,并分别与有限元强度折减法和公路设计规范推荐的方法(简称“规范法”)所得结果进行对比,以检验“改进影响带法”的适用性. 图6 土工格栅加筋路堤边坡示意图 “改进影响带法”分析上述加筋土坡的稳定性时,按式(1)计算出土工格栅单侧加筋影响带厚度δ,得到δ=39.98 cm.因为δ 采用强度折减法计算时,借鉴唐晓松等[13]的研究成果,路堤填土与地基土均以理想弹塑性模型来描述其应力应变关系,采用摩尔-库伦破坏准则,不考虑土体的剪胀性.土工格栅假定为只能承受拉力的理想弹塑性材料,其抗拉刚度(弹性阶段单位宽度格栅所受拉力与拉应变之比)为500 kN/m,屈服强度取土工格栅的设计抗拉强度Ta=10 kN/m.格栅与土之间设置界面单元,即筋-土界面单元.实测的界面阻力系数略大于1.1tanφ,这里偏保守地按1.1tanφ计算.根据介玉新等[14]的论证,强度折减法中只对土的强度进行折减,而格栅的强度不折减,即认为Ta是格栅的容许抗拉强度. 规范法按式(8)计算加筋土坡的稳定安全系数Fs,即: (8) 式中:Fsu为未加筋土坡的稳定安全系数,采用简化Bishop法计算;MR为筋材所能提供的抗滑力矩;MD为未加筋时土坡的下滑力矩;N为加筋层数;Ta为筋材的设计抗拉强度;R为滑弧的半径. 上述三种方法计算得出的该加筋粗粒土坡安全系数见表5.由表5可知,规范法的安全系数最小,强度折减法的最大,改进影响带法的居中,且与强度折减法更接近. 表5 三种方法计算的加筋土坡安全系数对比 规范法所得安全系数之所以最小,主要是因为它是将筋材和土的作用分开考虑的,没有从本质上考虑筋-土的相互作用,是其不合理之处.工程实例和理论分析都表明规范法偏于保守. 有限元强度折减法能够通过筋-土界面模型考虑筋-土的相互作用,并且可以计算出每层筋材的受力和应变分布,揭示加筋土结构的受力和变形规律,在理论上是更加合理的方法.但目前存在的关键问题是破坏判据不唯一,算得的安全系数依赖于破坏判据的选择.同时,计算比较复杂,对个人素质要求很高.因此,强度折减法在短期内还难以纳入规范. 相比较而言,本文提出的 “改进影响带法”,理论上考虑了筋-土的相互作用机理,计算方法上可按纯土坡来分析,比规范法更简单.“改进影响带法”算得的安全系数比规范法的高,一定程度上克服了规范法保守的问题;比强度折减法的略低,偏于安全.该法为计算加筋土坡的稳定性提供了一种新的思路. 1) 土工格栅加筋粗粒土的加筋影响带厚度与粗粒土的粒径大小、级配和土工格栅横肋厚度有直接关系. 2) 粗粒土的粒径大小、级配对加筋影响带厚度的影响仅用平均粒径d50来反映是不够的,还应将不均匀系数Cu、曲率系数Cc作为其影响因素纳入其中. 3) 加筋影响带厚度与土工格栅横肋厚度t成正比. 4) 根据初步试验结果,按Cu<5的均匀级配土和Cu≥5的非均匀级配土两种情况,分别给出了土工格栅加筋粗粒土的单侧加筋影响带厚度δ与土粒不均匀系数Cu和曲率系数Cc、土粒平均粒径d50以及土工格栅横肋厚度t之间的经验公式,较全面地考虑了粗粒土的级配、粒径大小对加筋影响带厚度的影响,同时还考虑了土工格栅横肋厚度的影响. 5) 土工格栅对粗粒土的间接加固作用在筋-土界面处最强,并随着离筋-土界面垂直距离Y的增大而逐渐减弱.据此,针对加筋层间距与加筋影响带厚度的相对大小,分析了不同情况下加筋影响带内土体抗剪强度增长量随Y值的变化规律,给出了具体的分布图.由此进一步完善了加筋土坡稳定性分析的“影响带法”,从而得到“改进影响带法”.具体算例表明,“改进影响带法”的计算结果介于规范法与强度折减法之间.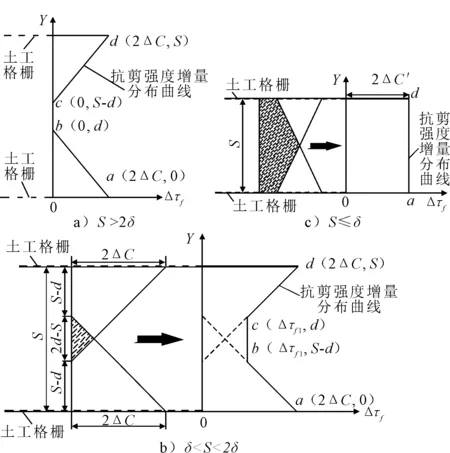
3 加筋土坡稳定性分析的“改进影响带法”

3 结 论

