基于LSTM网络的浮动单车需求量预测
肖 梅 张 颖 黄洪滔 郝艳军
(长安大学运输工程学院 西安 710064)
0 引 言
无桩式浮动单车无需定点停车,导致单车乱停乱放,挤占地铁等公共出入口、人行道交通车道等,造成单车在时空上分布不合理、道路资源的过度浪费,影响了城市交通秩序和形象,严重时甚至会造成交通阻塞.实现城市浮动单车需求量的准确预测,不仅可以为解决单车的乱停乱放提供理论依据,也可以更好地满足共享单车用户的出行需求,保障单车运营企业可持续、快速平稳发展.
国内外学者对单车显著性影响因素分析和需求量预测进行了大量的研究.在研究影响需求量因素方面:Fagnant等[1]利用西雅图骑行数据,提出了一种直接需求模型(direct-demand model),该模型根据产生量和吸引量估算与自行车相关道路条件,结果显示,需求量与交叉路口和路缘宽度和道路速度显著相关.Xu等[2]利用多源数据,提出了上海市共享单车兴趣点区域划分和交通分区的创新方法,揭示了上海市共享单车出行的分布特征并构建了多块混合动力预测模型准确预测了单车供需量.谭旭平等[3]为解决单车的投放和停车需求,针对城市用地的空间上的因素,考虑多种交通方式的换乘接驳,基于改进的logit模型对不同交通强度的交通区进行投放和停车需求的预测,提高了预测精度.在研究单车需求量预测方面研究方法多集中于统计回归模型和机器学习模型:Feng等[4]结合历史使用模式和天气数据,建立了基于随机森林预测模型来预测华盛顿地区自行车租赁需求量,相比于多元线性回归模型,预测结果和准确性都有很大提高.刘畅[5]基于网格划分理论、时间序列预测方法,构建了共享单车需求预测量ARIMA模型,但预测值的曲线拟合优度较低.Jia等[6]提出了一种两级高斯混合模型聚类算法,在此算法中考虑了自行车在站点间的迁移趋势和地理位置信息,并将实验结果与其他传统预测模型相比较,错误率减少了约8%.Wang等[7]综合考量自行车需求具有很强的随机性、时变性和非线性,提出了一种非线性RBF神经网络分位数回归算法来预测公共自行车站点需求量区间.Du等[8]以关联公共自行车出租站历史出行信息和时间为影响因素,分别建立了自适应粒子群优化小波神经网络(APSO-WNN)的公共自行车还借需求模型,对比粒子群优化小波神经网络(PSO-WNN),平均相对误差和均方误差分别下降了26.45%和36.31%.王立[9]通过对共享单车使用量的数据分析,重点研究了基于BP神经网络进行组合的非线性组合预测模型预测单车的需求量.杨军等[10]利用不同时段的共享单车需求数据,采用BP神经网络算法构建了四种不同激活函数下的需求预测模型.陈菁等[11]综合考虑校园区域和学生出行特征,应用小波神经网络预测区域需求量,实验结果表明:预测需求量的平均绝对误差和平均百分误差分别为0.983辆和14.36%.Soheil等[12]提出了广义极值(GEV)计数模型,以预测每小时内每个停车站点自行车的离开和到达的数量,整个系统总需求预测误差在5%以内,75%的站点到达和离开的预测误差在1以内.何郁波等[13]针对城市某一公共场所的单车使用量情况的时间序列,提出了ARIMA时序回归预测模型,对共享单车的使用情况进行了短期的预测,并验证了模型的可靠性.在深度学习中,由于LSTM神经网络具有长时记忆功能,且可以很好地解决梯度消失或梯度爆炸的问题,国内外学者将其运用在预测不同领域的问题:Xu等[14]通过深度学习方法建立了无站共享单车的动态需求预测模型,利用长短期记忆神经网络(LSTM NNS)预测不同时间间隔的共享单车出行量和吸引量,结果证明预测精度均优于传统的ARIMA、SVM等统计模型.Pan等[15]根据历史数据提出了一种基于两层深度的LSTM模型,预测未来一段时间内城市不同区域的自行车租赁和归还的情况,LSTM双层模型平均均方根误差为2.70,比DNN预测模型减少了14%.程肇兰等[16]提出了一种基于LSTM网络的铁路货运量预测模型,将预测结果与ARIMA预测模型结果相比较,LSTM网络预测效果更佳.耿立校等[17]为准确预测股票指数,提出了基于多源异构数据的长短期网络模型,并与卷积神经网络预测模型进行对比分析,结果表明,LSTM模型的预测准确率比传统模型更为优秀,更具可行性和有效性.
在综合考量影响浮动单车需求量的波动性及模型的稳定性的基础上,文中从时间因素、空间因素、天气因素、骑行因素上分析并得出预测模型的特征输入,构建了基于LSTM网络的单车需求量预测模型,实现了对城市浮动单车早晚高峰出行时段的精准预测,为浮动单车的管理提供了理论依据.
1 LSTM网络算法
LSTM的核心在于增加了三个门与一个记忆单元,分别是遗忘门、输入门、输出门,以控制信息在演进方向上的传递及增加控制门解决输入或输出问题.其主要是通过一个神经层和一个逐点相乘的操作来实现,很好地解决了长期依赖以及梯度消失和梯度爆炸的问题,LSTM网络模型结构原理图见图1.该模型向前传递的计算公式为
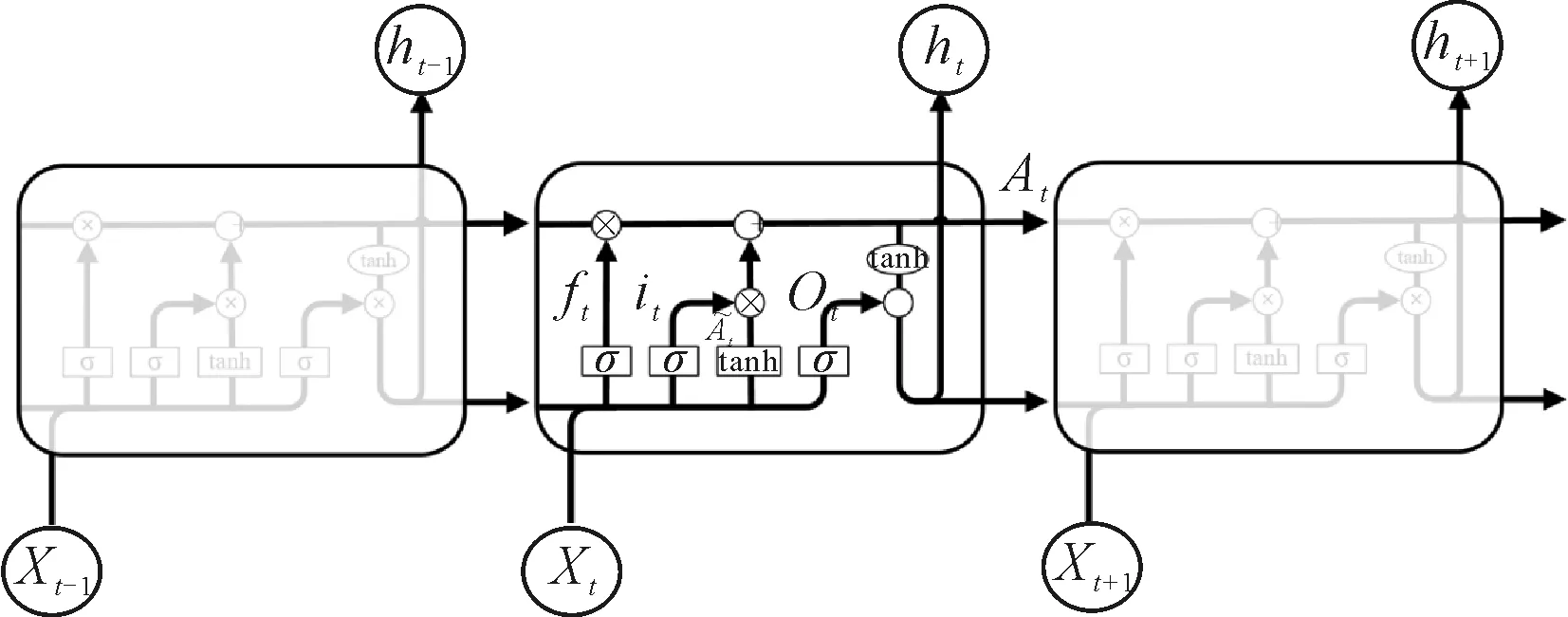
图1 LSTM网络模型结构
ft=σ(Wf·[ht-1,Xt]+bf)
(1)
(2)
(3)
Ot=σ(Wo·[ht-1,Xt]+bo)
(4)
ht=Ot·tanh(At)
(5)
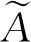
2 浮动单车需求量预测
2.1 数据预处理
文中采用的实例数据是通过解密开源的2017年的北京单车数据(https://biendata.com/competition/mobike/),样本原始数据的起止时间为2017年5月10—24日,数据集近两千万条,包括7个字段信息,见表1.对字段数据进行挖掘,初次选取了13个影响浮动单车使用的因素作为自变量.变量名称、表示符号及变量单位,见表2.

表1 原始样本数据示例

表2 变量的初步选取及相关描述
根据编码原理和字符串精度级别,7位编码长度对应的的面积为153 m×153 m,为使构建的研究区域更符合单车实际出行情况和短途骑行的特点,将其聚合成面积约为1.22 km×0.61 km的6位编码长度区域作为研究区域,在北京市空间位置分布见图2.

图2 北京市研究区域空间位置分布示意图
按照研究区域面积一定的筛选原则,随机提取了近5万条数据作为研究的样本数据并对原始数据集按每2 h进行重采样,划分成每2 h一个时段.经统计分析,出行的高峰时段为:早高峰08:00—10:00,晚高峰:18:00—20:00.为验证各网络模型的精度,将样本数据80%作为训练集,20%作为测试集.选取出行高峰时段(08:00—10:00)和平峰时段(12:00—14:00)的单车需求量预测作为验证模型精度的结果.
2.2 Spearman秩相关性检验
Spearman(SR)相关系数不仅用于衡量两个变量之间相关性检验,且样本数据不需要满足连续性和正态分布,同时也具有消除量纲的作用.为排除随机采样对SR相关系数结果的影响,以构建统计量的方式计算P值进行显著性检验.基于两者标准共同判断影响因素的显著相关性,见表3.式(6)为Spearman(SR)相关系数计算公式.

表3 相关性判断标准
(6)

表4为Spearman系数矩阵,表5为Spearman秩相关检验系数。由表4和表5可知,X1为城市功能区;X7为降雨天气;X8为高温出行;X9为风力级数;X13为骑行距离;X13的SR相关系数和检验值P都表现出非常弱的相关性,表明并不是影响单车使用的重要因素,推测可能是数据采集期间时间跨度仅为14天且天气情况较为稳定、各功能区流量集中导致需求量分布比较均匀,导致单车需求量波动不明显,因此以上影响因素均表现为不相关并剔除该变量.

表4 Spearman系数矩阵

表5 Spearman秩相关检验系数
而其他8个自变量间均存在相关性如:X3与X4强相关、X3与X11弱相关,X11与X12中相关等;与Y之间呈正相关的变量,如X3是由于存在公共交通的区域会更容易产生单车接驳需求;X5是由于居民日常出行更容易集中在1 d中的早晚高峰时段,例如,上下班时与公交、地铁接驳通勤等均会导致更大的需求量;与Y之间呈负相关的变量如:X6是由于用户在节假日出行需求比平时工作日的出行需求更迫切,对单车需求量更大.经分析对以上影响因素予以保留,并作为单车需求量预测模型的特征变量输入.
2.3 模型构建
基于Anaconda管理平台下的Python3.9开发环境,利用Tensorflow2.2与Keras2.3.1深度学习框架进行建模.将样本数据集随机划分为训练集80%,测试集20%,分别用于RNN、GRU、LSTM网络模型训练参数与测试模型精度,其中,LSTM网络预测模型运行原理见图3.为提高模型精度,模型中均采用0.001的Adam优化算法,tanh激活函数,Loss损失函数采用均方误差(mean squared error, MSE),计算公式为

图3 LSTM网络模型运行原理
(7)

2.3.1模型训练
对于基于时间序列预测的网络模型而言,t时刻单车需求量Yt的值,不仅受到t时刻的特征输入Xt的约束,同时还受到t-n(n=1,2,…)时刻的输出Yt-n及t-n时刻的特征输入Xt-n的约束.因此,模型的输入为t-n时刻的显著性变量数据集及标签数据集:Yt=(Yt-n+X(2,t-n)+X(3,t-n)+X(4,t-n)+X(5,t-n)+X(6,t-n)+X(10,t-n)+X(11,t-n)+X(12,t-n)+Xt),以此预测未来第N天的高峰时段:第(t+2)个时段,以及平峰时段:第(t+4)个时段单车需求量.交叉验证后训练集上模型预测精度达到最优时,停止迭代,得到LSTM模型参数:Units=3,Hidden_layer=32,Dense=2,Epochs=50,Batch_size=32,Dropout=0.2.
2.3.2模型评价指标
为了评估模型的预测结果,所用到的评价指标为:均方根误差RMSE,用来衡量观测值同真值之间的偏差;平均绝对值误差MAE,反映预测值误差的实际情况;拟合优度值R2,计算曲线拟合优度.
(8)
(9)
(10)
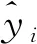
2.4 模型对比
为比较LSTM预测模型与其他预测模型的精度,本文另采用两种变种深度学习的预测方法:RNN预测模型和GRU预测模型.同理,搭建Python3.9开发环境,Tensorflow与Keras模块中的深度学习网络框架.样本数据训练集和测试集的划分均为8∶2,模型输入为经检验后的显著性变量数据集X及标签数据集Y.在训练集交叉验证后最终得到RNN模型参数: Activation=Softmax,Hidden_Layer=100,Batch_Size=128,Epochs=60,Dropout=0.3,Dense=2;GRU模型参数:Optimizer=Adam,Hidden_Layer=80,Batch_Size=64,Epochs=60,Dropout=0.5,Dense=2;损失函数均采用均方误差.其中,数据哑变量处理与数值归一化处理、模型结果评估与LSTM模型处理过程一致.
2.5 模型结果
为更加贴近实际单车出行情况,从位于20个不同位置的研究区域及14 d不同日期的数据集中随机选取了1 197条数据,133个时间滑窗序列测试样本,图4~6分别为各模型对早高峰时段及平峰时段单车需求量预测结果的真实值与预测值的拟合曲线及两者之间的差值曲线.由图4~6可知:LSTM预测模型中,预测值很高程度上预测了未来时间段的真实值;GRU预测模型预测效果次之,RNN预测模型预测效果较差.

图4 RNN网络预测模型

图5 GRU网络预测模型
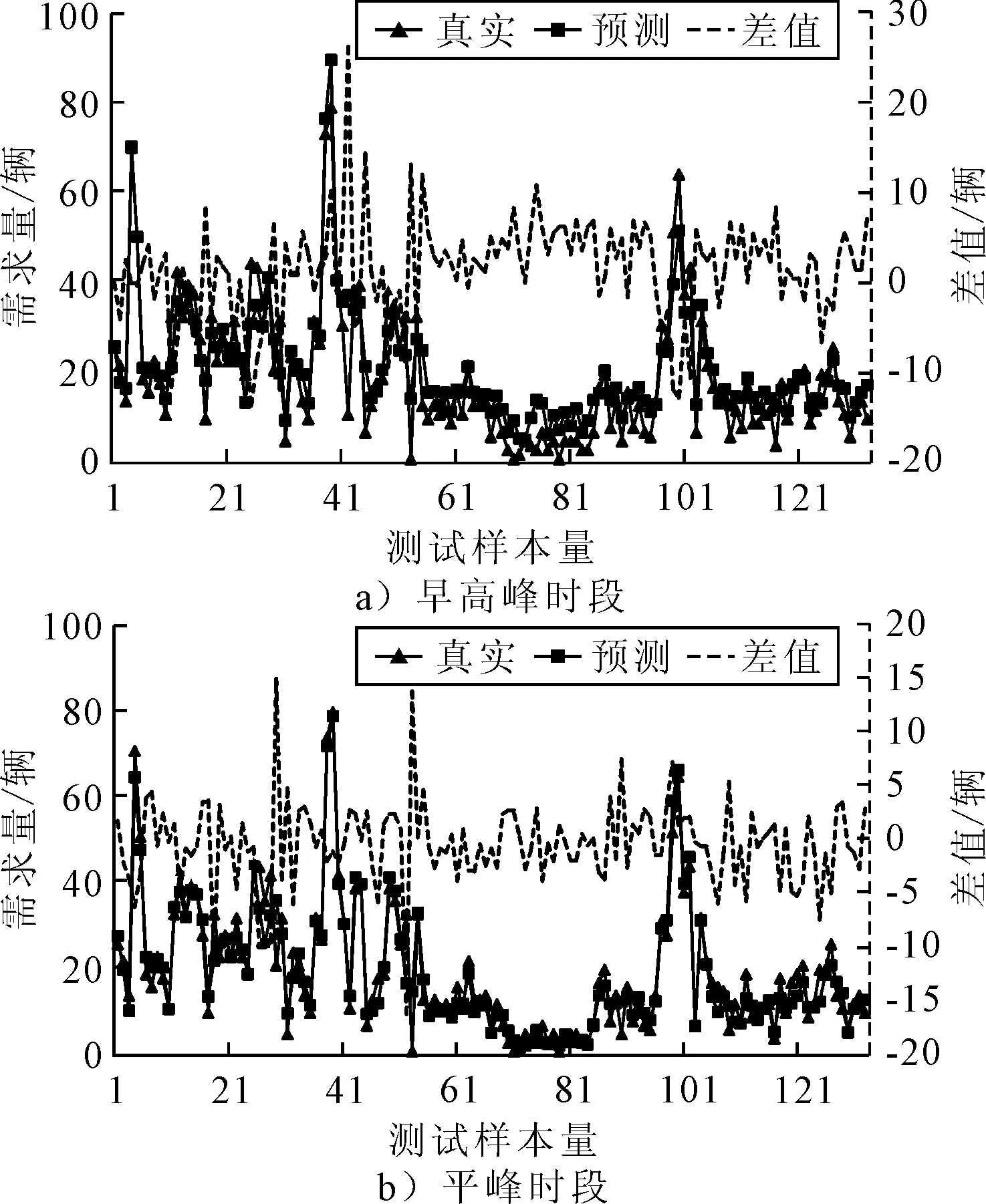
图6 LSTM网络预测模型
通过表6的评价指标对比分析,LSTM预测模型总体上优于两个对比预测模型.相较于GRU:LSTM优化了隐藏层节点,因此对时序的记忆能力更强;当时间序列距离增加时,RNN存在无法解决长时依赖,可能出现梯度消失或梯度爆炸等问题,然而LSTM受梯度消失问题的影响要小很多,拟合优度更高,且三个门与一个记忆单元的结构非常适用于处理与时间序列高度相关的问题.GRU与RNN进行对比:GRU除预测平均绝对值误差分别为7.14和4.53略高于RNN,其余评价指标均优于RNN,说明相比于简单的RNN网络结构而言,GRU虽然只有两个门,但构建庞大的网络时更加有力,效率更高.从预测结果整体看,浮动单车平峰时段的需求量预测比高峰时段预测效果更佳,由于高峰时段需求量对影响因素更加敏感,造成的曲线波动幅度较大,而平峰时段需求量受到的影响较小,从而更加平稳.

表6 模型评价结果
3 结 束 语
文中针对北京市内浮动单车出行时需求量的实际情况,从空间因素、时间因素、天气因素、骑行因素多方面考虑并分析了浮动单车不同时段的出行特征,并将其作为模型的特征输入,提高预测的精度和可信度,使预测模型更贴近现实情况.从深度学习算法的角度,结合浮动单车出行大数据,以及严格周期的时间序列,构建了一种基于LSTM网络的浮动单车需求量预测模型.为了验证LSTM模型的性能,分别构建了RNN网络预测模型和GRU网络预测模型,通过对比真实需求量和预测需求量数值的拟合曲线和各项预测结果评价指标,体现LSTM模型优越的影响因素记忆和预测性能,并且LSTM可作为复杂的非线性单元用于构造更大型深度神经网络,该模型成功为城市浮动单车的投放与后期的调度计划提供前瞻性理论支撑.下一步工作会深入研究模型超参对模型精度的影响,并且结合GIS数据模型,分析城市浮动单车在空间上的出行特征及预测模型的探索,例如:空间位置、空间形态及分布等,提高预测模型的普遍性和适用性.

