分布式工厂轮胎生产调度系统的模型分析

殷君芳

（江苏财经职业技术学院基础教学部，江苏淮安223001）

随着汽车保有量的大幅增长，轮胎的需求量与日俱增。越来越多的轮胎企业开始在不同地方建立分工厂来解决轮胎的生产和配送问题，并希望以此降低轮胎的生产成本和物流成本。这种分布式的工厂使得生产调度问题变得更加复杂，调度员需要在多个异地工厂之间统筹规划，考虑全局，力求找到一个满意的生产调度方案。若仅凭借人力通过经验找寻，不仅耗时耗力，也很难保证得到最优解。这正是研究分布式工厂轮胎生产调度系统的重要意义。

生产调度问题（Production Scheduling Problems）一直以来都是工业领域的热点和难点问题，往往具有极高的复杂性而被视为NP难问题[1，2]。假设某工厂在三个不同城市建设有三个分工厂，需要处理的下个月订单为100个，每个订单需要选择一个工厂进行轮胎的生产以及配送。虽然问题看似规模不大，但是共有3100种不同的生产调度方案。无论依赖于何种大型计算机都无法通过枚举各个调度方案在有生之年求出问题的最优解。此前，已有研究尝试过不少传统优化方法来解决生产调度问题，如整数规划、线性规划、牛顿法、共轭梯度法、三次插值法以及贪心法等等。但是对于生产调度这种NP难问题，面对如此巨大的搜索空间，传统优化方法往往无法得到满意的调度方案，因为算法往往难以收敛到全局最优解或是难以在可容忍的时间范围内搜索到较为满意的可行解，亟需新的高效的生产调度模型和算法。

此外，因为现实生产过程中的一些限制条件，生产调度问题往往具备多种约束。这些复杂现实约束进一步增加了生产调度问题的复杂性。可见，生产调度问题可以被视作带约束的大规模组合优化问题。

本文以国内某大型轮胎生产厂商的实际生产调度需求为背景，分析了分布式工厂的轮胎生产调度的模型。

1 问题描述

设工厂在M个地区设立了M个分工厂，每个地区仅有一个分工厂，每个月有N个订单等待系统调度。根据订单的产品规格、产量及提货点要求，寻求最优的工厂生产计划和运输方案，使得在满足约束的条件下，实现企业的生产成本和运输成本最小化。

图1展示了一种可能的订单、送达地和工厂三者之间的关系。每个订单都包含以下信息：客户编码、客户名称、送达方编码、送达方名称、产品编码、产品名称以及订单发货量。调度系统需要为每个订单分配一个工厂，该工厂负责这个订单的全部生产和配送。每个工厂里有若干种生产线，负责不同类别的产品加工。每个工厂包含以下基本信息：工厂编码、工厂名称、工厂所在城市。客户的信息由两部分组成：客户编码和客户名称。送达方的信息由三部分组成：送达方编码、送达方名称以及送达方所在城市。产品的信息由四部分组成：产品编码、产品名称、产品类别以及单位产品生产时间。并且每种生产线只负责一种产品，即产品类别数目与生产线种类数目相一致。

图1 订单、送达地和工厂的关系

举例而言，公司目前有三个分工厂，分别位于河北石家庄、江苏连云港和安徽马鞍山，那么三个工厂可以表示为：

生产调度方案包含客户编码、客户名称、工厂编码、工厂名称、送达方编码、送达方名称、产品编码、产品名称以及订单发货量。若分别将三个订单分配给F1、F2和F3三个工厂，那么三个订单对应的三条生产计划可以分别记作：

订单1的生产计划：（C1，汽车厂A，F1，石家庄生产基地，D2，常州武进区，P3，三号产品，50）；

订单2的生产计划：（C2，汽车厂B，F2，连云港生产基地，D4，武汉洪山区，P1，一号产品，20）；

订单3的生产计划：（C3，汽车厂C，F3，马鞍山生产基地，D1，郑州惠济区，P4，四号产品，5）。

设三个工厂的单位生产成本和运输成本分别如表1和表2所示，可以计算出上述三条生产计划的总生产成本和总运输成本。第一条订单需要50吨的发货量，在石家庄生产基地生产，需要运输到常州武进区，送达方所在城市是常州，所需产品类别是II类。根据表1可知其生产成本为相应单位生产成本乘以订单发货量，即15万元每吨乘以50吨，得750万元；根据表2运输成本可得10万元每吨乘以50吨，为500万元。综上，第一条订单的总成本是750万元加上500万元，为1250万元。同理可得，二号订单生产成本为200万元，运输成本300万元，总成本是500万元。三号订单生产成本为150万元，运输成本75万元，总成本是225 万元。表3总结了三条订单的各项成本明细。

表1 三个工厂的单位生产成本

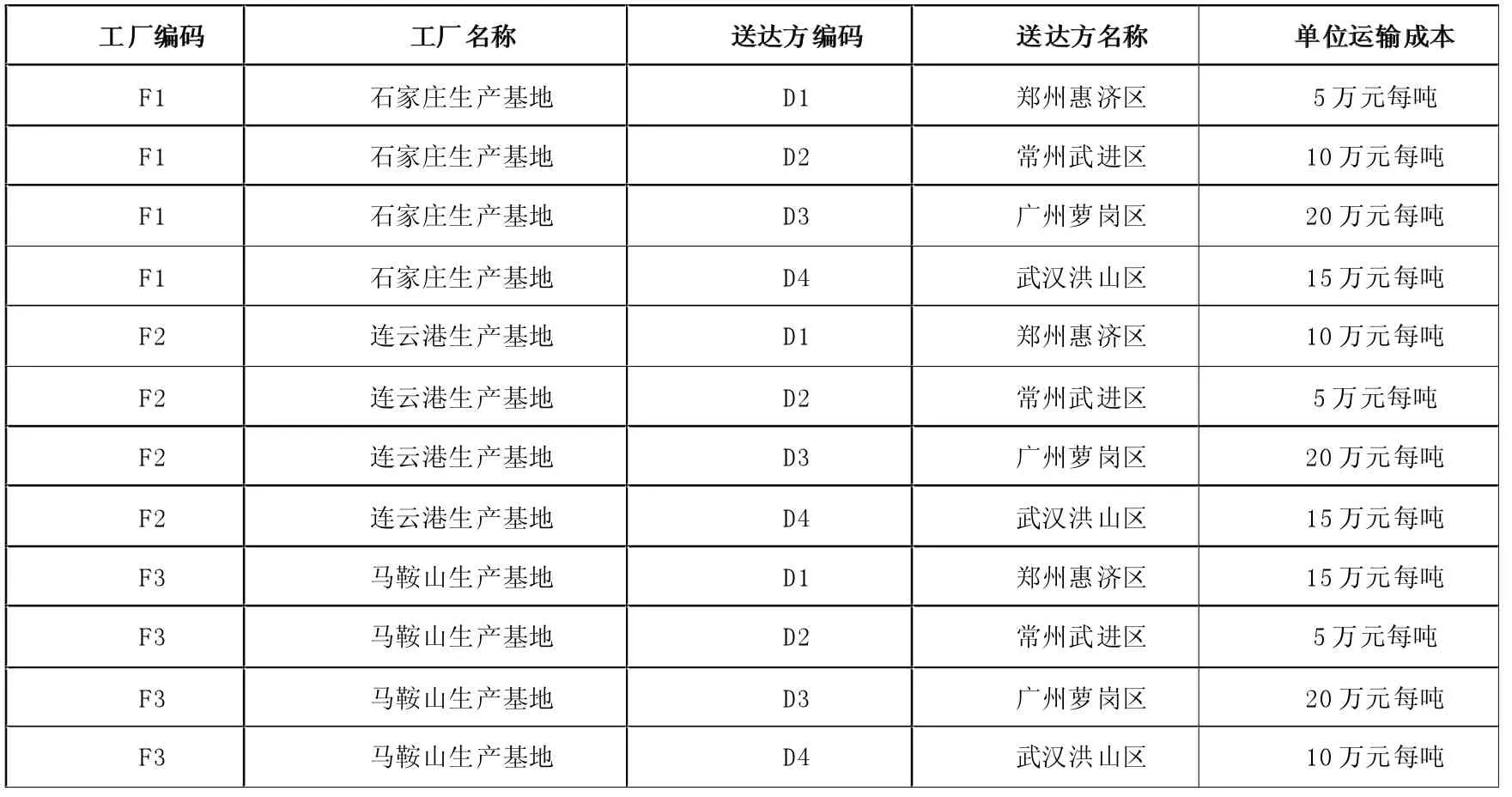
表2 三个工厂的单位运输成本

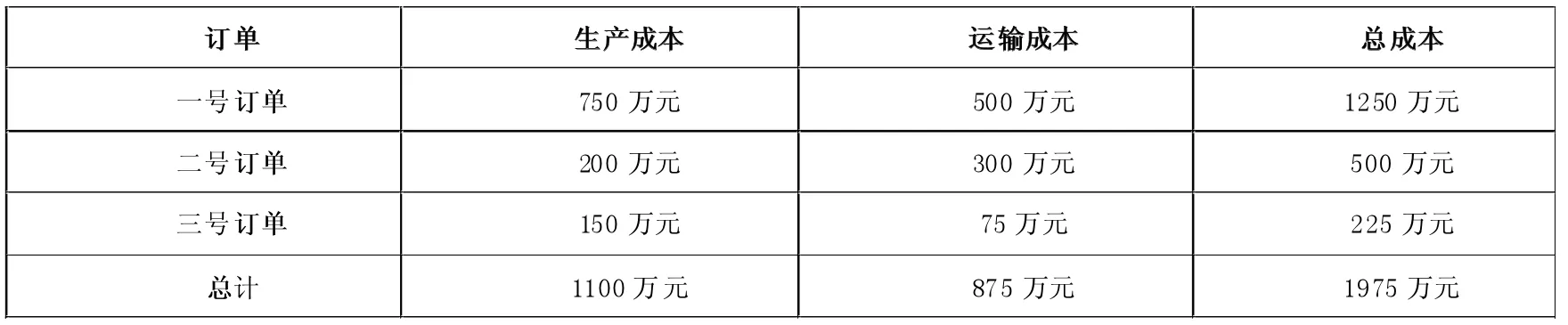
表3 三条订单的各项成本明细

2 轮胎生产调度系统的模型设计

2.1 优化目标分析

记运输成本为Ctransport，从工厂Fi到送达方Dj的单位运输成本记为Cij，则相应的总运输成本可以表示为式：

为了以备不时之需，各工厂都会留有库存，库存的存在可以降低生产成本，因为可从库存直接提取货物。所以并不是单位生产成本最低的工厂就能达到最低的总生产成本，还需考虑库存的影响。将Vij记为工厂F i里产品Pj的库存量，Vi记为订单Oi的库存提货量。当库存量高于订单发货量时，生产成本会减少到0，此时库存提货量等于订单发货量；当库存量不足订单发货量时，生产成本会减少一部分，此时库存提货量就等于库存量；而当库存量为0时，生产成本不变，库存提货量也为0。除此以外，当库存提货量不为0时，需要更新相应的库存量，即用当前库存量减去库存提货量，从而避免库存被多次计算。库存提货量以及库存的更新方式如式(4)和(5)，而生产成本将按式(6)进行更新。

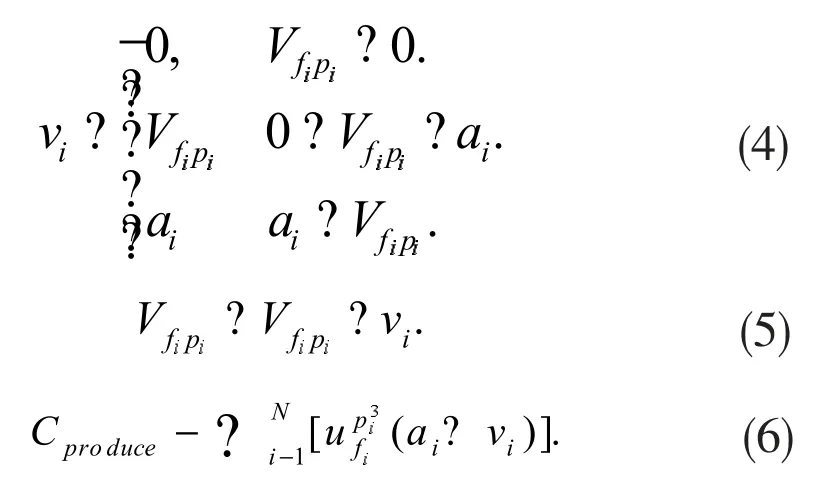
实际应用中，单位运输成本并不是一旦确定发货工厂和送达方城市后就完全固定的，而是一个随着发货量而变化的阶梯报价，可以看成一个类似电费的分段函数，不同范围的发货量对应着不同的单位运输成本。我们把这个阶梯报价表示为一个分段函数，记为L(x)，并假设该分段函数一共有T段。假设该分段函数的分段点表示为l=(l1，l2，…，lT-1)。并记此分段函数各阶段的函数值分别为h=(h1，h2，..，hT)，则这些函数值可以构成一个递减序列，即h1＞h2＞...＞hT。该分段函数表示为式(7)，新的总运输成本将由式(8)来表示，其中将原有的单位运输成本记号C ij改为以表示从工厂所在城市Fi到送达方城市Dj以发货量在第k段报价的单位运输成本。

2.2 约束条件分析

轮胎生产调度问题包含多个约束条件，包括：分批次发货约束、可生产产品约束、偏好工厂约束、生产线能力上限约束和生产线工作时间上限约束。下面将依次介绍这五大约束并分析其对优化问题的影响。

2.2.1 分批次发货约束

部分客户有时要求将同一订单生产的产品分批次发货，运输成本就等于每批次运输成本之和。

对于分批次发货约束，令zi表示订单Oi每批次需要的发货量，如果ai能被zi整除，每批次的运输成本都将一样；如果ai不能被zi整除，在最后一批运输时，运输成本则会有些不同。特别地，如果订单Oi不存在分批运输的约束，即货物将一次性全部运输到送达方所在城市，那么就令zi等于ai。所以，新的运输成本计算公式如下：

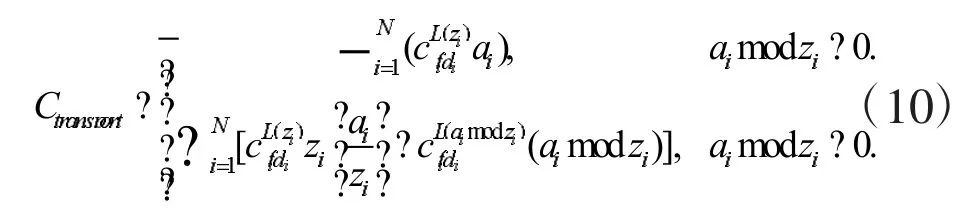
2.2.2 可生产产品约束

虽然分布式工厂的布局里有很多工厂，但不代表每个工厂都有能力生产所有种类的产品，因此在为每个订单分配生产工厂时，需要使得工厂有能力生产目标产品，否则这种安排就毫无意义。对于可生产产品约束，定义工厂Fi的可生产产品集合为Si，则有Si=⊆{P1，P2，…，Pk}。这项约束将被表示为式：pi∈Sfi（11）

2.2.3 偏好工厂约束

在选择工厂时，客户会要求部分订单只能从所约定的偏好工厂里选择。此时该工厂必然满足可生产产品约束。为了简化问题，把偏好工厂直接和订单绑定，即每个订单存在一组偏好工厂。如果某条订单没有偏好工厂约束，则所有工厂都是其偏好工厂。对于偏好工厂约束，将Xi记作订单Oi的偏好工厂集合，则Xi⊂{F1，F2，…，FN}。这个偏好工厂约束可以表示为式：pi∈Xi（12）

将生产产品约束和偏好工厂约束这两项约束合并为可选工厂约束。将Ui记作订单Oi的可选工厂集合，则Ui⊂{F1，F2，…，FN}。从而可选工厂约束可以表示为式：pi∈Ui（13），且显然有Ui=Sfi∩Xi。

2.2.4 生产线能力上限约束

2.2.5 生产线工作时间上限约束

生产线工作时间上限与上一项约束类似，每条生产线每月的工作时间有上限，否则会对生产线造成不可逆转损害。因为订单组每个月会更新一次，即每次进行调度安排时，保证此次生产不会违反这项约束即可。

综上，该生产调度问题的优化目标将由式(9)确定，并且受到式(10)(13)(14)和(15)的约束。

3 总结

生产调度问题一直以来都是工业领域中重点研究的问题。每得到一次改进，相关工业的生产成本就会有一定的降低，生产效率也会有所提升。轮胎作为生活中的重要工具，其大规模分布式生产离不开调度与优化。随着轮胎的需求不断增加，轮胎生产需要一个更符合实际的优化调度模型。本文以最优的总成本为目标，给出了分布式工厂的轮胎调度问题的精确数学表述，得出优化目标的函数表达式，然后分析了多种约束的限制条件，并给出所有约束的精确表述，建立了带约束的生产调度模型。

由于生产调度问题过于复杂，本文的调度模型虽可以满足所有约束，但仍然存在一些不足并需改进。文中提出的模型将一条订单派给一个工厂去生产，忽略了多个工厂合作完成一条订单的可能性。如果多个工厂同时有所需产品的存货，同时分给这些工厂就能大大降低生产成本，从而以更大幅度减少总成本。这种情况下问题会变得更复杂，更难处理。新的调度模型将由工厂序号组成的序列转为两个自然数矩阵，即两个矩阵的每一行都代表1条订单而其中每一列分别代表在该工厂需要为该订单生产的数量以及库存的提取数量。虽然问题不再属于组合优化问题，但是搜索空间会更加广阔，解的数量将急剧增加。