风速对海面长波红外偏振度的影响研究

宿德志,刘 亮,刘陵顺

(1.海军航空大学航空基础学院,山东 烟台 264001；2.海军航空大学岸防兵学院,山东 烟台 264001)

1 引 言

随着红外技术的发展,红外偏振成像技术逐步成为近年来国内外研究的热点,并在复杂背景下的目标探测中展现出广泛的应用前景[1]。基于强度的红外探测方法主要利用目标和背景温度差进行识别,由于海面背景的影响,当温差不大时,无法保证海面背景下目标探测与识别的正确率与效率。红外偏振探测能够充分利用目标表面的粗糙度、折射率等信息,有效地抑制背景,提高目标探测率。目前,国内红外偏振探测研究热点是金属、表面涂层的偏振特性[2-4],而对海面偏振特性的研究较少。事实上,在海面复杂场景下偏振成像比普通红外成像能探测到范围更广的目标[5],研究海面红外偏振特性对复杂海况下的目标探测与识别、目标隐身与反隐身以及海上搜救等应用都具有重要意义[6]。

研究表明海面具有很明显的偏振特性,其红外偏振特性分析常采用双向反射分布函数进行描述,因为海浪的尺度要大于红外波段的尺度,可以用几何光学近似来解决问题,一般采用基于微面元理论的Cook-Torrance模型[7]。宫剑针对海面场景舰船目标的长波红外偏振检测进行了实验研究,表明了红外偏振成像的有效性[8]。张景华研究了海面场景下舰船长波红外波段的偏振特性,给出了偏振度计算模型,但是只研究了平静海面的情况[9]。唐军武指出,在一定探测角范围内,可以忽略低风速对海面偏振的影响[10]。COX.C等人根据海面闪光出现的概率实验给出了海面微面元斜率分布与风速的关系[11],广泛用于抑制海面耀光和偏振研究[12-13]。景琳通过仿真研究给出风速越大海面的粗糙度越大,且激光主动成像中海面反射的Stokes矢量分布更加发散[14]。柳祎采用微面元理论建立了偏振度计算模型,并研究了目标表面粗糙度对偏振特性的影响[15]。从以上分析可知,海面的粗糙度对海面偏振特性有较大影响,而风速很大程度上决定了海面的形状和粗糙度,对偏振探测的准确性和效率影响很大,所以有必要对不同风速条件下海水的偏振特性进行研究。本文采用海浪谱和快速傅里叶变换的方法模拟海面形状,利用Radtherm软件,结合中国台站实测数据计算了不同条件下海面辐射和天空大气辐射,并根据建立的偏振度计算模型,仿真了风速和探测角等因素对海面偏振特性的影响。

2 海面建模

常用的海浪谱建模方法主要包括两种,线性叠加法和线性滤波法,这两种方法能够反映海浪的随机特性,并且线性滤波法建立在FFT(快速傅里叶变换)基础之上,这种方法能够比较迅速的仿真不同风向和不同风速下的大尺度海浪的起伏特性,在海浪实时模拟等方面得到了广泛应用。本文采用线性滤波法模拟海面,该方法需要对白噪声进行傅里叶变换,然后在频域内进行滤波,最后作傅里叶逆变换从而得到海面高度场分布。具体仿真过程为,设二维随机粗糙海面在x和y方向的长度分别为Lx和Ly,M、N为等间隔的离散点,则相邻点的间距Δx=Lx/M,Δy=Ly/N,对海面上每点坐标可以表示为:

xm=mΔx;yn=nΔy;m=-M/2+1,…,M/2;n=-N/2+1,…,N/2

(1)

则海面高度场函数可以表示为[16]:

(2)

其中,S(kmk,knk)为二维粗糙海面的方向谱,且kmk=2πmk/Lx,knk=2πnk/Ly,N(0,1)表示均值为0,方差为1的高斯分布,为使f(xm,yn)为实数,需要傅里叶系数满足关系式F(kmk,-knk)=F*(-kmk,knk)和F(kmk,knk)=F*(-kmk,-knk)。本文海浪功率谱采用PM谱,方向扩展函数采用ITTC谱[17]。

3 海面场景长波红外偏振模型

3.1 红外偏振特性分析

光的偏振态可以用Stokes矢量S=[IQUV]T,其中,I表示辐射强度,Q表示水平和垂直光强差值,U表示+45°和-45°方向光强差值,V表示圆偏振光强度,偏振探测中通常忽略该分量。则偏振度可以用Stokes矢量表示:

(3)

通常用BRDF来描述光波在物体表面反射过程中的一般光学特性,其定义为沿出射方向辐亮度dLr(θi,φi,θr,φr)与沿着入射方向辐照度dEi(θi,φi)的比值,模型如图1,具体表达式为:

(4)

根据微面元理论,基于Torrance-Sparrow BRDF模型表达式如下[18-19]:

M(θi,φi,θr,φr)

式中,σ代表目标表面粗糙度；θ为微面元法线zμ与目标表面法线z所成夹角；φ为入射光和反射光的方位角；β为入射方向与微面元法线zμ所成夹角。M(θi,φi,θr,φr)为穆勒矩阵其中,θ、θi、θr、φi、φr、β(i,r分别表示入射和反射方向)满足以下关系:

cos2β=cos(θi)cos(θr)+sin(θi)sin(θr)cos(φr-φi)

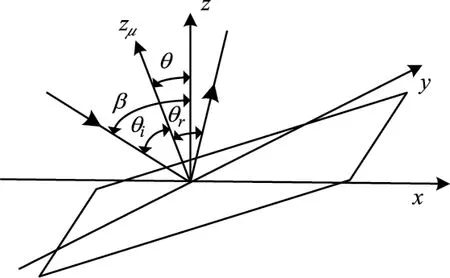
图2 微面元模型几何关系Fig.2 Geometry relation of Micro-surface model

根据Stokes矢量与Muller矩阵的表达式,可以得到入射光的Stokes矢量Si与反射光Stokes矢量Sr关系式:

(5)

当入射光为非偏振光时,其Stokes矢量可以表示为[1 0 0 0]T,又根据菲涅尔反射定律可以求得:

(6)

其中,ηi为参考平面之间的变换的旋转角,有:

(7)

(8)

反射Stokes矢量[20]为:

当采用微面元模型时,每个面元均假设为镜面反射,不妨设入射面和反射面在同一平面内则ηi=0,此时,对每个面元而言其偏振度为:

(9)

由菲涅尔反射定律可知,自然光经物体表面反射时会与表面发生作用,从而产生部分偏振光,同样,物体在向外发出热辐射时也会出现偏振效应。根据基尔霍夫定律,当光入射到不透明物体时,其发射率和反射率之和为1,即:

(10)

其中,εp和εs分别表示平行分量和垂直分量的发射率。则红外辐射过程的偏振度为:

(11)

3.2 海面场景偏振分析

如图3所示,对于海面来说,进入探测器的能量分为四部分:海水热辐射Ie、海面反射的太阳辐射Is、海面反射的大气辐射和天空散射光辐射Ir、海面到传感器之间的路程辐射Iatp,探测器接收到的辐射能量:

图3 海面红外辐射模型Fig.3 The model of sea water infrared radiation

Id=τ(εIe+RIs+RIr)+Iatp

(12)

其中,τ为大气透过率;ε,R分别为海面发射率和反射率。由于长波红外波段太阳辐射能量较少,若避开耀光区域可暂不考虑太阳辐射Is的影响,同时由于路程辐射Iatp中,总体上不表现出偏振现象,对海面场景偏振效应的影响很小[9],因此这里只考虑海水热辐射Ie和大气辐射和天空散射光辐射Ir两个影响因素。第i个海面微面元的偏振度表示为:

(13)

其中,Ipi表示微面元i反射和辐射产生的p波总和,Isi表示微面元i反射和辐射产生的s波总和。Ipi,Isi计算方法如下:

Ipi=Rpi·Iri+εpi·Iei

Isi=Rsi·Iri+εsi·Iei

定义辐射反射比αi如下:

则:

(14)

由上式可知,微面元的偏振度与面元的入射角θi和辐射反射比αi有关。由菲涅尔反射定律和基尔霍夫定律可知,在红外反射过程中,其垂直分量始终大于平行分量,而在红外发射过程中,其平行分量始终大于垂直分量,因而综合考虑反射和发射过程,当辐射反射比αi=1时,其偏振度为零,当αi<1时,反射光强大于辐射光强,偏振光垂直分量大于平行分量；当αi>1时,辐射光强大于反射光强,偏振光垂直分量大于平行分量。

4 RadTherm仿真

一般而言,海面场景αi的求解较为困难,因为大气辐射和天空散射光辐射Iri的影响因素较多,所以本文采用RadTherm软件仿真计算了海面场景的长波红外偏振特性,RadTherm是一个专业的热分析软件,可以仿真不同经纬度、海拔高度、天气状况、云层等环境因素影响,全面考虑热辐射、热传导和对流等传热方式,快速准确求解各个场景下瞬态温度分布和辐射强度,且张景华[9]和沈敦亮[21]已验证了RadTherm软件在部分场景下计算结果的可靠性。

4.1 仿真流程

采用海浪谱和快速傅里叶变换法模拟生成不同风速下的海面高度场模型,仿真的海面区域为512 m×512 m,两个方向的采样点数目均为512个。

1)由于高度场模型无法直接导入RadTherm软件,需要将高度场模型转化为面元数据,本文将粗糙海面分割为522242个三角形面元,并建立obj模型文件,同时计算出每个面元的法线方向。

2)将obj模型文件导入RadTherm软件,仿真时间选为4月,上午6∶10到第二天上午6∶10共24小时,仿真波长设置为8～12 μm,天气条件为薄雾,湿度大；并根据中国台站实测数据导入海面温度变化曲线(图4)和气象数据,仿真计算后可以得到每个面元的辐射亮度、大气辐射和天空散射光辐射亮度,部分仿真结果如图5。

图4 24小时海面温度变化曲线Fig.4 The 24-hours curve of sea-surface temperature

图5 海面红外辐射仿真结果Fig.5 Simulation of sea water infrared radiation

3)根据探测器位置和每个面元的法线方向求解出各面元的入射角θi,根据菲涅尔反射定律可得到Rpi和Rsi,再利用RadTherm计算出的辐射亮度、大气辐射和天空散射光辐射亮度,就可以应用式(14),求解出该面元的DOPi。

4.2 仿真结果

如图6(a)为仿真得到的海面场景辐亮度变化曲线,可以发现海面的辐亮度较大,也就是说发射强度大于反射强度,因此长波红外波段偏振光垂直分量大于平行分量,而且海水比热容大,昼夜温差小,相比于天空和大气辐亮度变化较小,图6(b)为根据仿真结果计算的风速为10 m/s,探测角为45°时海面的24 h平均偏振度变化曲线,可以发现从下午6∶00开始,由于没有太阳照射,天空和大气辐亮度迅速降低,使得海面平均偏振度增加较为明显。

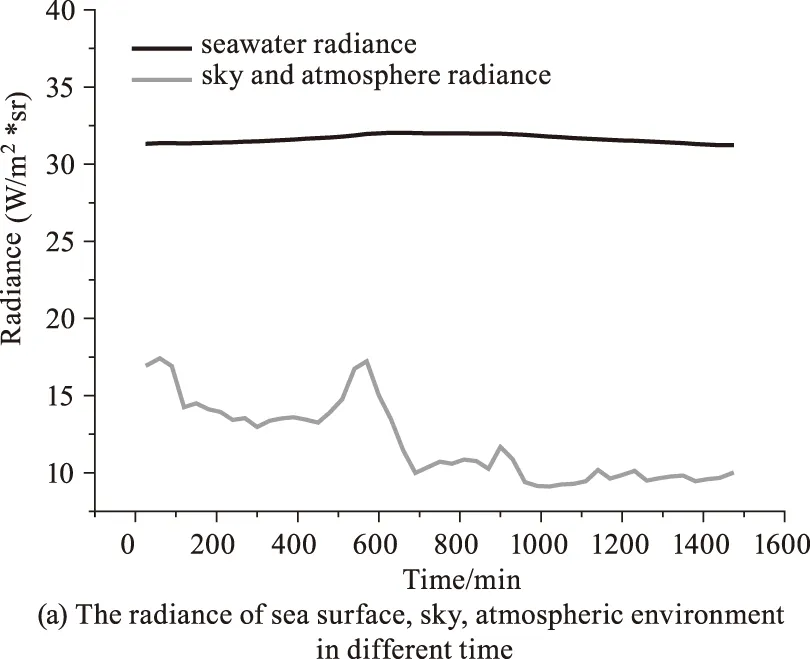
图6 不同时间内海水和天空大气辐亮度、平均偏振度变化曲线Fig.6 The radiance of sea surface,sky,atmospheric environment and average polarization degree in different time

4.2.1 稳定性

由于RadTherm软件只能导入固定的模型文件,而粗糙海面是动态变化的,即使相同风速和气象条件下,其表面形状也是不断变化的,为验证本文仿真方法的稳定性,在相同风速条件下随机生成了10个不同的海面模型,应用RadTherm软件进行仿真,其偏振度结果如图7所示。

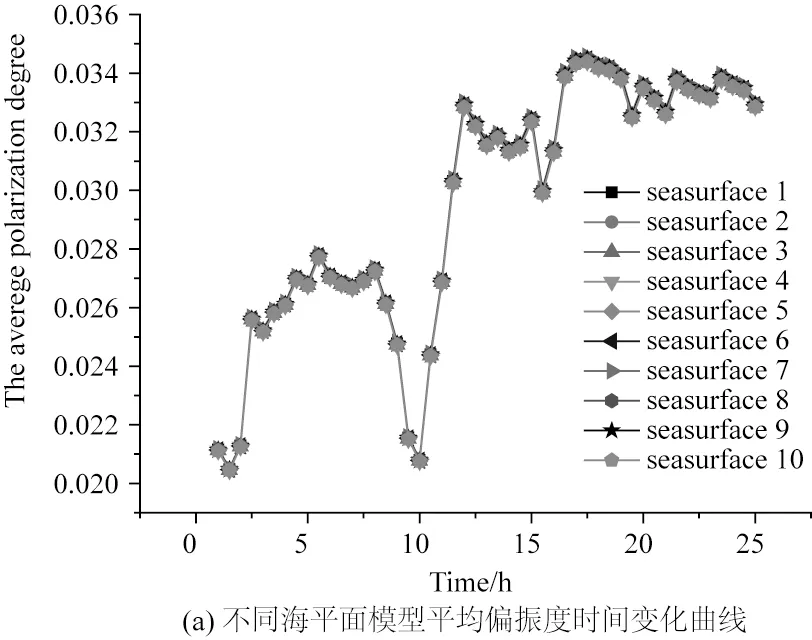
图7 不同海平面模型平均偏振度和最大偏振度的时间变化曲线Fig.7 The average and maximum degree of polarization in different time

从图7可以看出,虽然随机生成的10个海面高度场模型是不同的,但是其平均偏振度和最大偏振度等参数是一致的,也就是说这种仿真方法是稳定的。

4.2.2 不同风速和探测角对偏振度的影响

根据菲涅尔反射定律可知,当入射角为布儒斯特角附时,反射光会达到最大偏振度,若同时考虑发射偏振和反射偏振,能够达到最大偏振度的探测角一般在80°左右[22],那么随着风速的增加,组成海面的各微面元法向会偏离竖直方向,这个角度会如何变化？我们模拟了风速分别为1 m/s、5 m/s、10 m/s、15 m/s、20 m/s和23 m/s时,各个探测角下的平均偏振度,结果如图8所示。

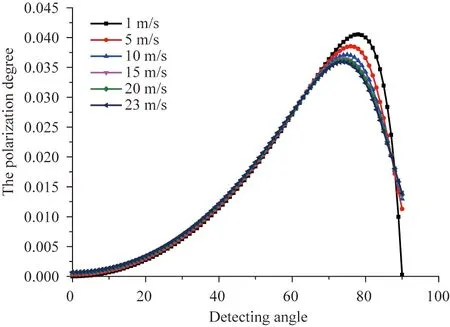
图8 不同风速下偏振度与探测角的关系Fig.8 The degree of polarization versus detecting angle with different wind speeds

从图8可以看出,随着风速的增加,峰值偏振度减小,对应的探测角也减小。同时我们计算了45°和60°探测角下所有面元与探测器轴向的夹角,并统计如图9所示。

从图9可以看出,当风速较小时,各面元的入射角分布主要集中在探测角附近,随着风速的增加,入射角的分布几乎对称的向两侧拓展。根据图8可知,探测角小于80°时,偏振度是随着探测角增大而增大的,当入射角分布向两侧对称拓展时,向右拓展的面元偏振度会增加,向左拓展的面元偏振度会减小,平均偏振度会如何变化？我们仿真了探测角分别为40°、60°和80°时,海面平均偏振度随风速的变化情况,如图10所示。从图中可以看出,40°探测角时,偏振度随风速增加而增加,60°探测角时偏振度变化很小,80°探测角时,偏振度随风速增加而减小。可见不同探测角下,其变化关系不一致。因此,我们计算了0°～90°探测角下,风速分别为4 m/s、10 m/s、15 m/s、18 m/s、20 m/s、23 m/s与风速为1 m/s时所有面元的平均偏振度差值,如图11所示。从图中可以发现探测角为63°时,海面偏振度基本不受风速影响,所以海面场景的偏振探测应使探测器的工作角度为63°附近,可以最大程度的减少海面风浪对探测结果的影响。

图9 45°和60°探测角下,各面元入射角的分布情况Fig.9 The distribution of the incident angle with the detecting angle 45° and 60°

图10 不同探测角下偏振度与风速关系Fig.10 The degree of polarization versus wind speeds with different detecting angles

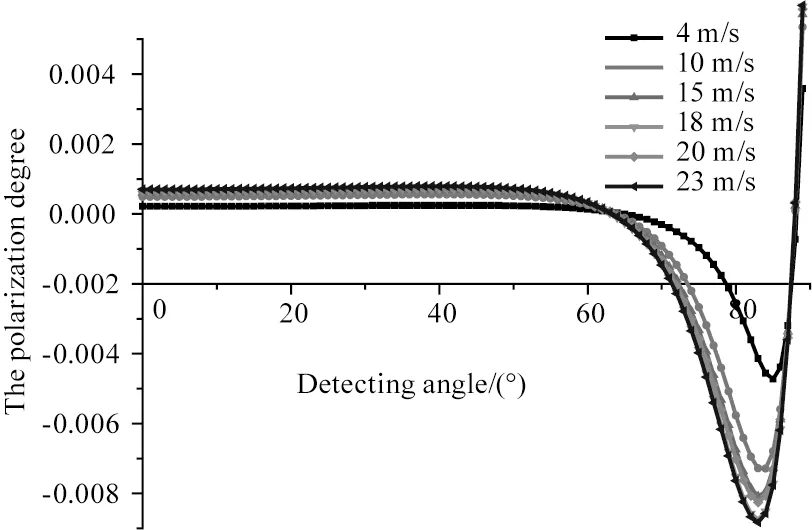
图11 偏振度差值与探测角关系Fig.11 The difference of degree of polarization versus detecting angles

5 结 论

本文利用海浪谱和快速傅里叶变换法模拟了海面,综合考虑了海面场景下红外发射和反射偏振效应,根据双向反射分布函数的微面元模型,结合菲涅尔反射定律和基尔霍夫定律给出了偏振度计算模型,最后利用RadTherm进行了仿真。仿真结果表明,海面长波红外偏振特性昼夜变化较大,其最大偏振度探测角随风速变化很小,探测角在80°附近时,海面平均偏振度取得最大值。随着风速的增加,各面元入射角的分布几乎对称的向两侧拓展,使得在较小探测角时,偏振度随风速增加而增加,而在大探测角时,偏振度随风速增加而减小。探测角为63°时,海面偏振度基本不受风速影响,所以海面场景的偏振探测应使探测器的工作角度为63°附近,可以最大程度的减少海面风浪对探测结果的影响。为简化计算本文仿真时认为天空和大气为自然光,同时用辐亮度代替了辐射强度,可能在一定程度上引入一些误差,会在后续工作中进一步完善这部分工作。