基于二阶梯度的红外小目标检测方法

汪 伟,许德海,任明艺

(四川虹美智能科技有限公司,四川 绵阳 621000)

1 引 言

近年来,随着红外成像技术在红外预警、导弹制导、民航、森林防火、医疗等领域的广泛应用,红外小目标检测技术日益成为红外成像系统的关键技术,并形成当前红外图像处理领域的研究热点。在红外图像中,远距离的目标占用的像素很少、没有明显的纹理形状特征,且受到强烈的背景杂波及噪声的影响,给小目标检测带来了极大的挑战[1]。目前红外小目标检测方法主要包括两类[2]:检测前跟踪和跟踪前检测。检测前跟踪即根据原始图像建立候选点,利用候选点轨迹进行跟踪,最后在候选点轨迹附近根据灰度分布进行检测；跟踪前检测即对目标进行背景抑制,然后进行阈值分割的到候选目标,根据目标的连续性来确定目标。

本文主要研究跟踪前检测方法。目前典型的跟踪前检测方法包括形态学滤波[3](主要为Top-hat方法)、Max-Median滤波方法[4]、小波变换[5]的方法等。Top-Hat方法和Max-Median方法的优点是方法简单,处理速度快,在目标信噪比较高的情况下检测准确度较高,但是在复杂背景情况小检测效果较差。Chen等人[6]提出一种局部对比度检测方法(LCM),但该方法容易受到背景高亮噪声的干扰,提高虚警率。Wang等人[7]提出一种基于二阶梯度的弱小目标检测技术(FB),该方法处理过后的显著图能明显提高信噪,但极值公式推导错误并且阈值设置不合理,容易造成虚警。

与其他方法不同,本文将红外小目标检测问题表述为显著区域检测问题。在一幅图像中,复杂的背景边缘通常不具备各向同性,而小目标通常具备各向同性的特点,且在红外图像中,小目标通常相当于一个局部极大值,因此小目标往往可以吸引人眼的注意。由于远距离热成像系统的光学点扩散函数(Point Spread Function,PSF)为高斯型函数[8],因此小目标具有类似于高斯型的特性。换而言之,“各向同性”目标相对于“各向异性”的背景是显著的。因此本文基于小面模型设计二阶方向导数滤波器,并根据极值条件得到二阶极值图像,然后对二阶极值图像进行形态学滤波进一步抑制杂波得到显著图,最后本文设计了一种新型的基于灰度分布的阈值计算方法,进而实现二值化并提取目标。本文方法所获取的显著图具有极高的信噪比,所设计的阈值方法可获得较高的检测概率及较低的虚警率。

2 原 理

对于小目标而言,在图像中相当于一个局部极大值,因此可以利用一阶导数或者二阶导数并根据极值理论实现小目标的提取。但由于红外图像通常受到各种噪声的干扰,信噪比很低,基于一阶导数的小目标检测方法通常虚警率很高,检测效果极差。为此,本文利用二维离散正交多项式对原始图像的局部灰度分布进行拟合,然后采用二阶方向导数滤波器进行滤波,得到方向导数图,随后根据极值定理计算二阶极值图,之后对二阶极值图进行多结构元形态学滤波并进行融合获取显著图,最后利用像素灰度分布获取自适应阈值,并分割提取目标。本文方法流程如图1所示。

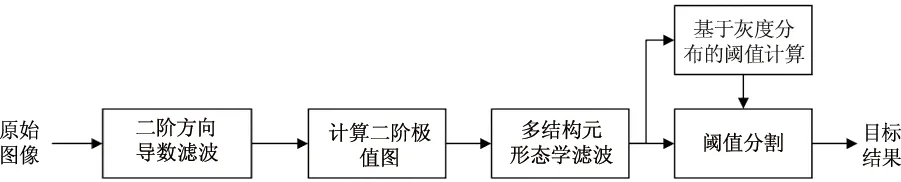
图1 本文方法流程图Fig.1 Method flowchart of this paper

2.1 正交多项式

本文令离散正交多项式阶数为0～N-1。这些多项式是唯一的,称为离散切比雪夫多项式(discrete Chebyshev polynomials)[9]。

假定离散的整数指标集R是对称的,即如果r∈R,则有-r∈R。令Pn(R)为n阶多项式,采用迭代的方式构建离散正交多项式。

定义P0(r)=1,假定P0(r),…,Pn(r)已经定义,通常情况下,Pn(r)=rn+an-1rn-1+…+a1r+a0,Pn(r)必须与每一个多项式P0(r),…,Pn-1(r)正交。因此有如下的n个方程:

(1)

式中,k=0,…,n-1。

这些方程是关于未知数a0,…,an-1的线性方程,可以采用常规方法求解。最初的5个多项式为:

(2)

对二维离散正交多项式,则采用对两个一维正交多项式集求取张量积的方法得到。令R、C为指标集并分别满足前述的对称性条件(即如r∈R则-r∈R,如c∈C则-c∈C)。令{P0(r),…,PN(r)}是R上的离散正交多项式,{Q0(c),…,QM(c)}是C上的离散正交多项式,则集合{P0(r)Q0(c),…,Pn(r)Qm(c),…,PN(r)QM(c)}是R×C上的离散正交多项式。

2.2 正交多项式对图像灰度拟合

令Pn,n=0,…,N-1表示离散正交多项式基函数,η表示独立同分布的噪声,g表示原始图像灰度。则有:

(3)

式中,Ki,i=1,2,…,N-1为多项式展开的系数,正交多项式Pi(r,c),i=1,2,…,N-1满足:

(4)

则系数Ki的最小二乘估计为:

(5)

本文采用的邻域为R={-2,-1,0,1,2},C={-2,-1,0,1,2},忽略噪声的影响,并只考虑前10个离散正交多项式,则有:

(6)

式中,Ki,i=1,2,…,10为多项式展开的系数,即:

Pi(r,c)={1,r,c,r2-2,rc,c2-2,r3-(17/5)r,(r2-2)c,r(c2-2),c3-(17/5)c}

(7)

2.3 滤波原理

利用式(6),可得中心点(r=0,c=0)的二阶偏导数为:

(8)

根据多项式Pn的正交性,可得:

(i=4,5,6)

(9)

在实际计算时,可采取模板卷积的方式同时完成图像灰度拟合及二阶方向导数滤波,即:

(10)

式中,Wi,i=4,5,6为卷积模板系数:

根据极值理论[10,12]当g(r,c)满足下列条件:

(11)

则对应像素g(r,c)为极大值点(即可能的小目标)。

1)在计算K4、K5、K6时,是分别利用模板W4、W5、W6对原图像进行卷积的方式进行的。

2)在实际计算时,可只利用第二个和第四个条件,即:

(12)

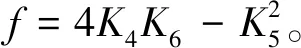
3)为了降低计算量,在实际计算中可进行简化。模板W4,W5,W6的系数分别提取出来,即:

式中:

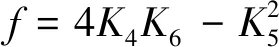
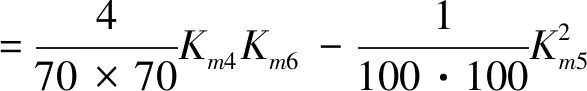
(13)

式中,Km4,Km5,Km6分别为使用Wm4,Wm5,Wm6模板滤波后的图像。

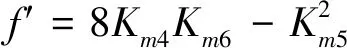
(14)

则滤波过程可表示为:

(15)

由于式(15)为整型运算,因而可以避免复杂的浮点运算,从而大幅提升运算效率。

图2(a)为原始图像,图2(b)～(d)分别为M4、M6、M5模板对原始图像滤波后的图像,图2(e)为根据(b)、(c)、(d)计算得到的二阶极值图,图2(f)为原始图像响应图,图2(g)为二阶极值响应图,可以看出与原始图像相比,二阶极值图像中背景杂波被极大地抑制,且目标得到大幅增强。

图2 各通道滤波与极值图像Fig.2 Each channel filter and extreme value image

3 多结构元形态学滤波

经过二阶方向导数滤波后,目标得到大幅度增强,但仍旧容易受到图像中背景边缘的影响使得检测结果中产生虚警。为此,采用线形结构元的形态学滤波进行处理以抑制背景边缘的影响。由于某个方向的线形结构元形态学滤波仅能抑制该方向的背景边缘,而背景边缘的方向无法预知,因此考虑结合多个方向的线形结构元进行形态学滤波,并采用适当的方式进行融合以抑制不同方向的背景边缘,获取显著图。

(16)

式中,⊕为膨胀运算符；⊖为腐蚀运算符;∘,·分别为开运算符和闭运算符。

采用如下的准则对各个开、闭图像进行融合得到显著图:

(17)

式中,fo为开运算融合图;fc为闭运算融合图;S为获取的显著图。

4 基于灰度分布的阈值分割

在弱小目标检测中选取一个合理的阈值至关重要,阈值选择的过低容易产生虚警,阈值选择过高则可能造成漏警,因此需要针对显著图S设计一个较为合适的阈值分割方法。本文提出一种新颖的基于灰度分布的阈值计算方法,该方法能够有效地去除掉显著图中的背景和杂波,并保留真实目标。该方法的步骤如下:

1)首先将显著图归一化

(18)

式中,min(·)为最小值函数;max(·)为最大值函数;round(·)为取整函数。

2)计算归一化极值图像的直方图

h(x)=∑i,jδ(I(i,j)-x)

(19)

式中,g为归一化显著图;δ(·)为离散时间单位脉冲函数。

3)建立灰度分布查找表M

M为3行N列的表格,其中N为h(x)中值不为0的灰度级的数目。M中的第一行依次存储h(x)不为0的灰度级,M中的第二行依次存储h(x)不为0的每一个灰度级所包含的像素数目,M中的第三行为h(x)不为0的灰度级与前一个h(x)不为0的灰度级的差,即M(3,i)=M(1,i)-M(1,i-1),其中i>1。

4)遍历M的第三行,如果M(3,i)>5则令阈值Th=M(1,i)。

5 实验结果及分析

为了验证本文方法对弱小目标检测的有效性和可靠性,选用Max-Median方法和LCM方法和FB方法对小目标检测效果进行对比分析。实验分成两组,一组对比不同场景下各种方法的背景抑制效果,另一组则比较不同方法中阈值的计算对于弱小目标检测的影响,从而验证本文方法的有效性。

5.1 背景抑制效果对比实验

本组实验采用4组场景的红外图像进行测试,第一组场景中包含两个目标,第二组和第三组场景为云层背景中,第三组场景为背景为太阳目标信噪比极低。图3为4种场景算法处理后的目标显著图。

图3 4种算法处理后的目标显著图Fig.3 The target salience graph after four kinds of algorithm processing

图3(a)为4种场景的原始红外图像,图3(b)～图3(e)分别为Max-Median方法、LCM方法、FB方法和本文方法处理后的目标显著图。可以看出,LCM能够提高信噪比但是对于背景的抑制效果最差,Max-Median方法、FB方法、本文方法对背景抑制较好,但对于信噪比较低的场景,Max-Median方法和FB方法滤波后的图像背景中仍存在部分杂波。

图4为4种场景目标红外图像处理后的三维响应图。图4(a)为原始图像的三维响应图,可以看到场景中目标淹没在云层中,较难分辨,经过Max-Median方法、FB方法和本文方法处理后目标较为突出,但是Max-Median方法依然存在较多的背景杂波不利于后续目标的提取,FB方法虽然在场景一和场景二中对于信噪比的提升优于本文方法,但对于场景三和场景四复杂背景中对信噪比的提升明显较差,而本文方法在四组场景中对信噪比均有较好的提升,处理后的图像杂波更少、目标更加突出明显便于后续目标的提取。

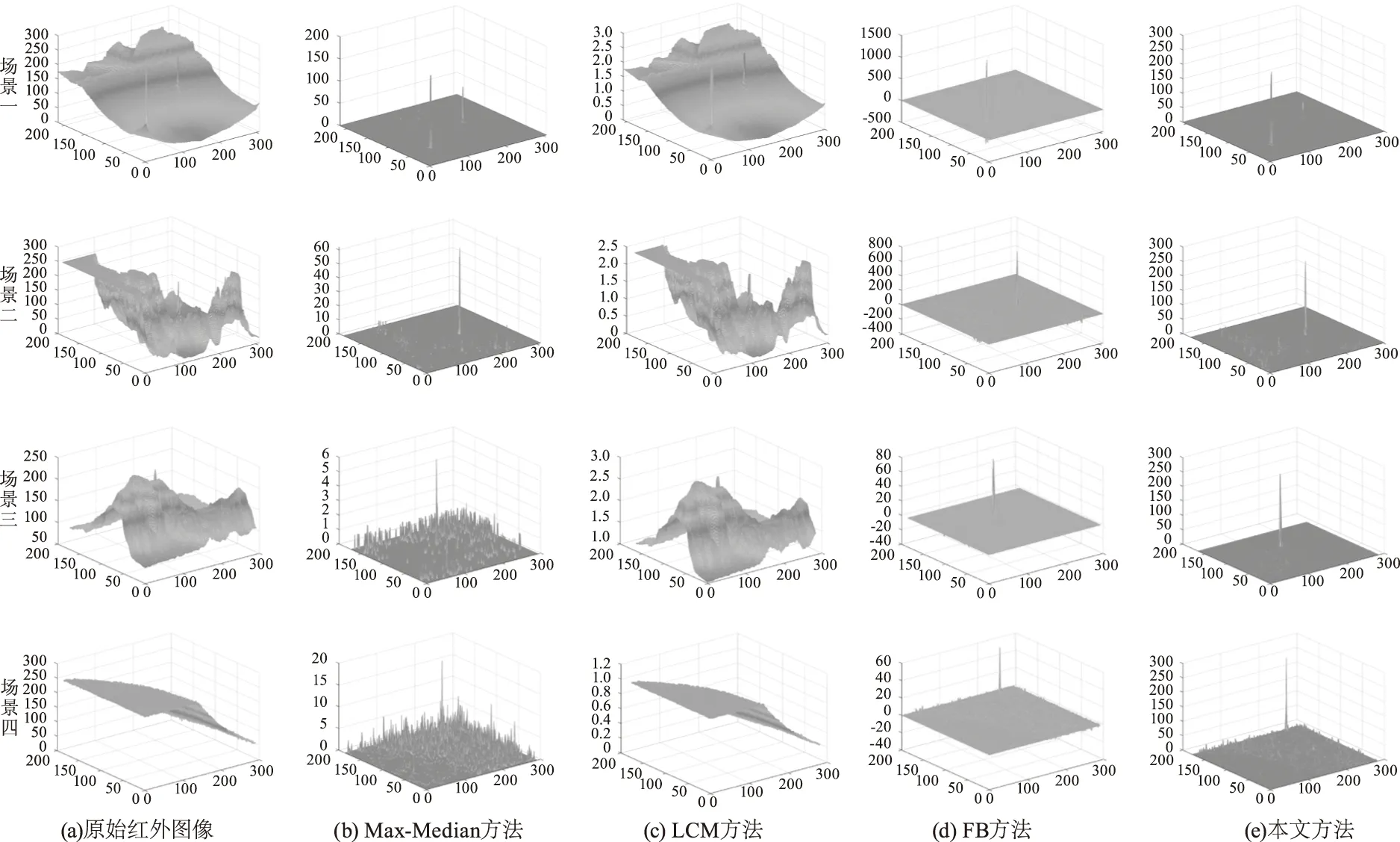
图4 4种算法处理后的三维响应图Fig.4 Three-dimensional response diagram processed by four algorithms

5.2 阈值方法对比实验

本实验的目的为验证本文设计的阈值方法的有效性,因此选用Max-Median方法和FB方法做比较,其中Max-Median方法选用自适应阈值进行目标分割,这种方法是一种经典的阈值分割方法用于小目标检测,该方法的阈值计算如下:

Th=μf+3·σf

式中,μf为待检测图像的灰度均值;σf为待检测图像的标准差;Th为计算得到的自适应阈值。

FB的阈值计算方法选用参考文献[7]提供的阈值计算方法。采用三种方法分别对4组场景进行阈值分割得到的结果如图5所示。

图5 阈值分割方法比较图Fig.5 Comparison chart of threshold segmentation methods

图5为自适应阈值方法、FB阈值分割方法和本文提出的阈值分割方法比较结果,可以看到,自适应阈值方法对于信噪比较高的场景中,会获得较好的分割结果,但对于信噪比较低的场景中结果较差,而对于FB阈值分割方法,在单目标情况下FB方法能够准确的提取目标,但是在多目标情况下产生了漏警,分析其原因为在阈值选择的时候过于随意,参考文献[7]中的阈值选取为显著图最大值的0.3倍,因此在无目标的背景下同样会造成虚警,在多目标情况下易造成漏警,本文提出的阈值分割方法提取目标更为准确,虚警率更低。

6 结 语

本文提出一种基于二阶梯度的红外弱小目标检测方法,首先通过根据小面模型设计了二阶方向导数滤波器对图像进行滤波将原始图像分解为不同的方向通道,然后根据极值定理计算极值图像,随后对极值图像进行形态学滤波以增强目标能量的同时进一步抑制背景杂波,最后对极值图像进行归一化处理并统计其直方图,利用直方图及图像灰度分布选取合适的阈值并进行阈值分割以得到最终目标位置。实验结果表明该方法在信噪比极高的复杂背景下准确的对弱小目标进行检测。