基于梯度提升回归算法的刀具磨损评估模型

项海婧，宫爱红，胡明茂

（湖北汽车工业学院 机械工程学院，湖北 十堰 442002）

机床部件间关系复杂，一旦发生故障，维修人员难以凭借简单仪表加以诊断［1］，因此在加工生产过程中实时、高效、准确地识别刀具的磨损状态，对确保工件品质及设施安全具有重要意义［2］。近年来国内外对刀具磨损状态监测的研究已经取得了一定的成果，多传感器融合技术多次应用于机床各种信号的采集和检测［3］。通过对采集的数据进行时域、频域分析，提取刀具磨损相关特征［4］，进行特征选择后将得到的与刀具磨损强相关的特征输入回归模型、支持向量机（support vector machine，SVM）等机器学习模型进行模型训练，最后将训练好的模型用于刀具磨损预测［5］。黄华等［6］研究了刀具状态的监测方法，采集了刀具铣削过程的电流电压信号。康振兴［7］发现刀具磨损的声发射信号与刀具磨损状态具有明显的对应关系。Vadim等［8］建立了基于声发射信号的刀具磨损诊断系统，进行了钢坯1035铣削实验，使用小波分解从AE谱中信号滤波，并基于傅里叶变换进一步分析，取得了较好的成果。关山等［9］提取信号特征，并用最小二乘支持向量机进行刀具磨损识别。江雁等［10］利用EEMD与SVM结合的算法对刀具磨损状态进行研究，证明了SVM方法在刀具磨损状态识别中的可行性。Mehdi Nouri等［11］采用切削力法建立了切削力系数跟踪模型。现阶段刀具磨损评估模型大多只分析单一测试信号，没有考虑铣削条件的变化情况，因此很难实现动态情况下刀具状态的识别［12］。许多学者通常使用SVM进行刀具磨损识别，需要根据经验来确定合适的核函数以及其他参数，增加了模型的不确定性［13］。针对以上问题，文中构建了基于梯度提升回归算法（gradient boosting regression,GBR）的刀具磨损评估模型，采集铣削加工中心的铣削力、振动及声发射信号，以铣削力、振动信号时域、频域指标和声发射信号滤波后的最大幅值处频率作为特征值，以对应工况下的刀具磨损量为目标值来构造数据样本，将重组的特征输入到GBR模型进行训练与优化。

1 信号特征提取

1.1 力、振动信号特征提取

力、振动作为周期高频信号，常用的特征提取方法主要分为时域特征提取和频域特征提取。时域特征包括均方根Xrms、峭度Xkur、脉冲指标Ximp、歪度指标Xske、裕度指标Xclear、波形指标Xshape。

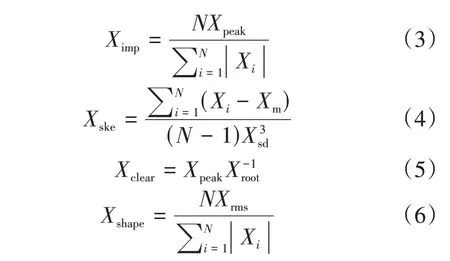
式中：Xi为信号点；Xm为信号均值；Xsd为信号标准差；Xpeak为信号峰值；Xroot为信号根值；N为信号总数。基于信号频谱值提取的频域特征包括频率均值Fm、频率有效值Frms和频率重心Fc。

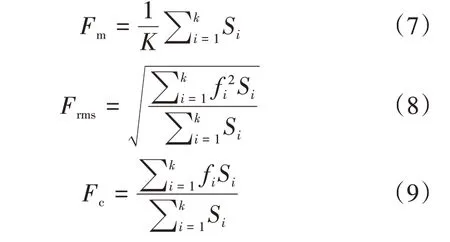
式中：K为频谱值总点数；f为第k条谱线的频率；S为时域信号序列的频谱序列。

1.2 声发射信号特征提取

声发射（AE）信号比力和振动信号能更早检测出刀具形变和断裂情况，是非稳态、易受外界干扰的信号，系统接收到的多为二次处理均方根（RMS）值，如图1a所示。采用信号滤波和频谱分析组合方法来提取AE信号特征。首先对AE信号进行带通滤波，以降低噪声干扰，然后对滤波后的信号进行傅里叶变换转换到频域分析，最后提取出最大频谱幅值处所对应的频率作为特征，结果见图1b。

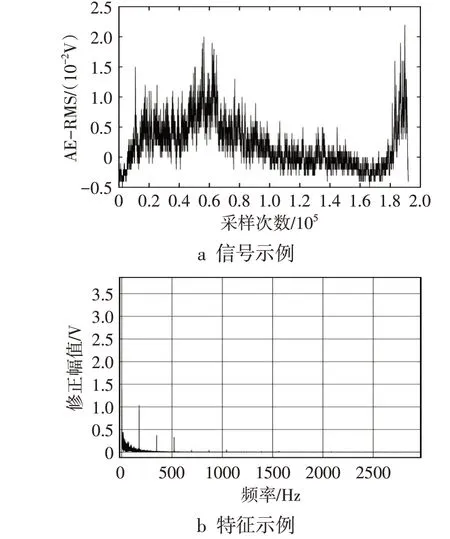
图1 AE信号

2 GBR模型

梯度提升（Gradient Boosting）是集成学习方法，通过串联合并多个简单的学习算法（弱学习器）来提高模型的准确性和泛化能力。常见的是GBR模型，以合并多个决策树来构成更强大的模型，虽然对参数设置更敏感，但合适的参数会提高模型的精度。GBR模型的算法步骤如下：假设数据集

的损失函数为L（y,f（x））。初始化模型为

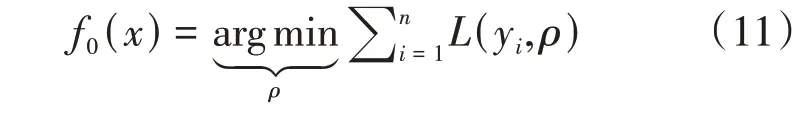
迭代生成M个弱回归模型，计算每个弱回归模型下每个样本的损失函数负梯度值rim和对应的梯度下降步长ρm：

更新模型：

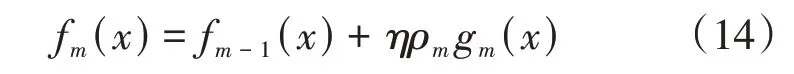
式中：η为学习步长；gm（x）为弱回归模型。输出最终模型：

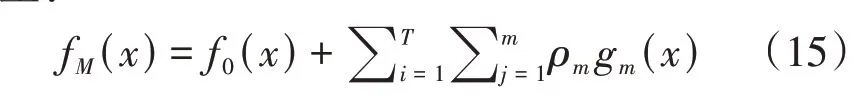
使用过程中，GBR模型精度受迭代次数、学习步长和弱学习器数量的影响较大。为防止模型出现欠拟合或者过拟合问题，采用参数网格搜索交叉验证的方法来提升模型精度，不需要对数据进行缩放，适用于二元特征与连续特征同时存在的数据。

3 仿真实验与预测结果分析

3.1 仿真实验数据获取

实验数据来源于2010年美国PHM协会公开数据集，机床实验条件如表1所示，重复进行6次全生命周期实验，分别记作c1～c6。每次都测量机床x、y、z方向的铣削力、振动加速度以及AE信号的均方根值，走刀后测量后刀面的磨损量。选择公开数据集c1、c4和c6作为本次模型的学习样本。刀具磨损量全生命周期变化趋势如图2所示。

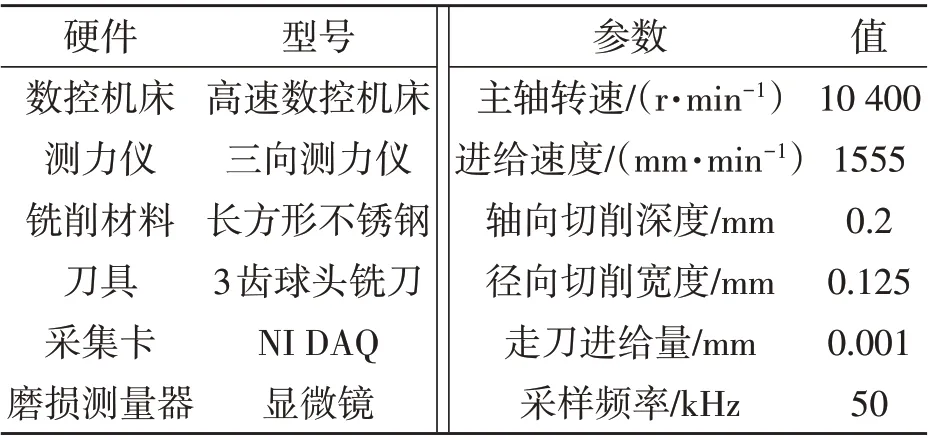
表1 机床实验条件

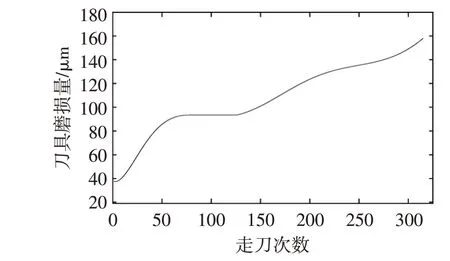
图2 刀具磨损量变化趋势

3.2 GBR刀具磨损评估模型预测结果分析

基于python语言和sklearn框架分别建立线性回归、贝叶斯岭回归、弹性网络回归、SVM和GBR模型，并引用2010年美国PHM协会公开数据集数据进行测试。通过比较预测结果与真实值的平均绝对误差（MAE）、均方误差（MSE）和R2来判断模型的效果。模型训练前，选择c4和c6作为训练数据集，c1作为测试样本。训练样本数量为630，测试样本数量为315。原始数据集中的数据为高频时序数据，采用时频域特征提取方法来处理数据集，并基于训练集的均值和标准差来对测试集进行归一化处理。模型输入特征维度为55维，即

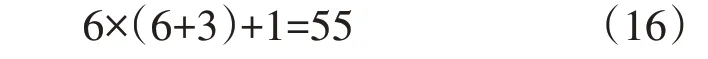
标签维度为1维。各特征值数量级差别较大，对特征值进行归一化处理，最后设置5次交叉验证、其余参数为默认值进行训练。

各模型每次交叉验证的准确值如表2所示，在训练集上的MAE、MSE和R2值见表3，各模型在训练集上的预测结果如图3a～e所示。通过表2可以看出，各模型在训练过程中的交叉验证得分存在一定的波动，其中线性回归模型波动最大，GBR模型波动最小。刀具磨损是非线性非稳态的变化过程，训练数据选取方式对模型精度影响较大，GBR模型在刀具磨损评估中具有较高的稳定性和精确性。由表3可看出，各模型MAE和MSE的数值存在较大的差异，但R2值比较接近。其中GBR模型R2值为最高的0.99。结合图3a～e，上述现象表明各模型在训练集的预测上都有较好的效果，GBR效果最好，几乎能完全预测出刀具的磨损情况。

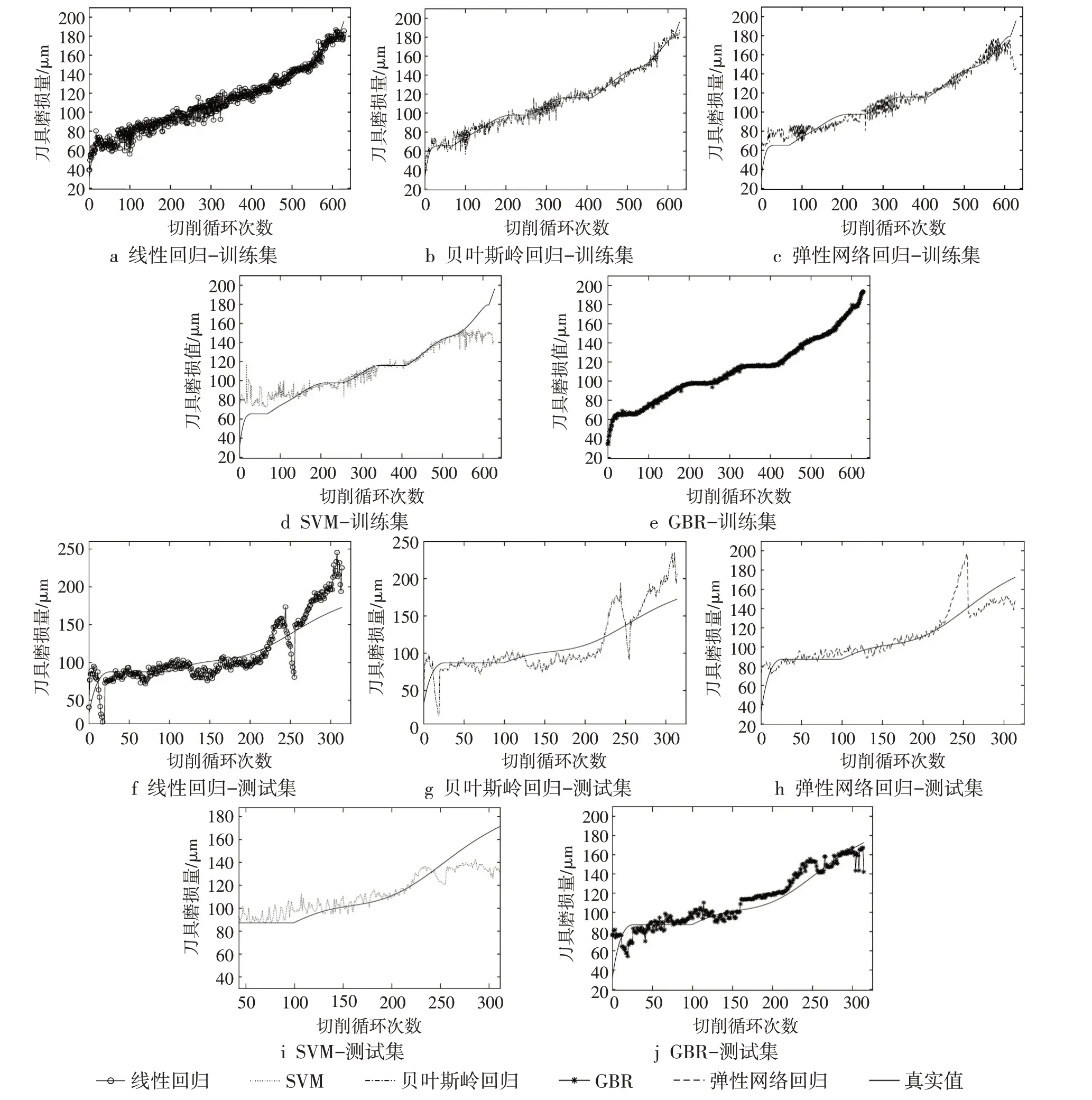
图3 各模型在训练集和测试集上的预测结果

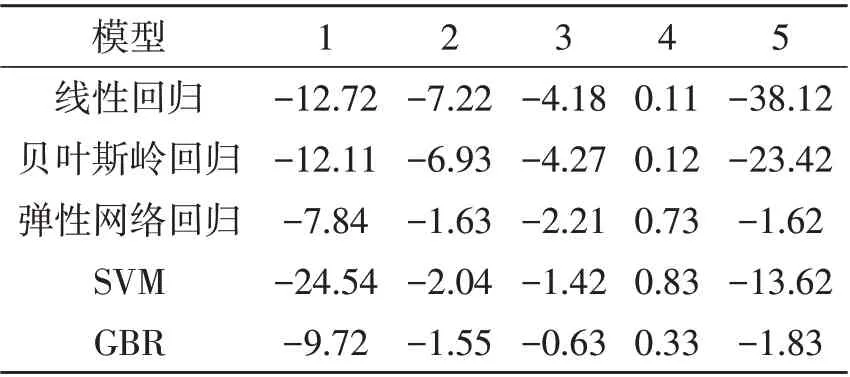
表2 训练集5次交叉验证准确值

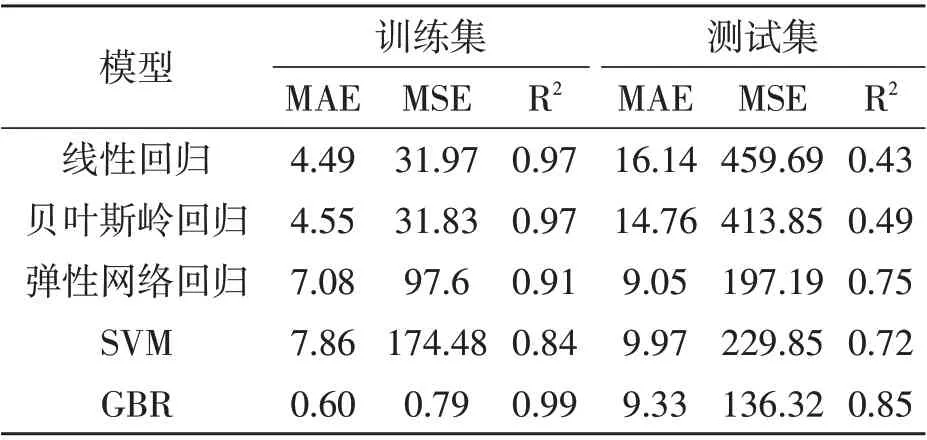
表3 各模型MAE、MSE和R2值

为了测试模型的泛化能力和检验模型是否存在欠拟合、过拟合的现象，采用c1独立测试模型精度，采用网格搜索优化模型参数的方法来确定模型的最佳参数。各模型在测试集上的MAE、MSE和R2值见表3，预测结果如图3f～j所示。由表3可看出，GBR模型在测试集上的R2最大值为0.85，说明GBR模型相较于其他回归模型在刀具磨损预测中具有更高的泛化能力。结合图3f～i可看出，其他回归模型在测试集中均出现预测值极大偏离真实的极端情况，而GBR模型在测试集中的预测值与真实值具有较高的一致性，未出现明显的偏离情况。常用的训练集和测试集划分比例为4：1，且同属于1个大样本，但实验中训练集与测试集的样本数量比为2：1，属于独立分布数据集，从侧面验证了GBR模型在刀具磨损预测中的有效性和优越性。

4 结论

文中构建基于梯度提升回归算法的刀具磨损评估模型，利用信号处理技术从时域和频域2个方向对刀具的铣削力、振动和声发射数据进行特征提取，丰富了模型样本特征维度，基于集成学习算法组合弱学习器构建出梯度提升回归模型，最后验证了其有效性。与其他回归模型相比，梯度提升回归模型在刀具磨损评估中具有较高的精度性和稳定性。文中仅测试数控机床的铣削加工数据，后续考虑增加训练数据以提高模型的精度，并应用于车削等其他加工中。