基于粒子群优化算法的PID控制液压防抱死系统
陈鑫,胡明茂,廖子文
(湖北汽车工业学院 机械工程学院,湖北 十堰 442002)
防抱死制动系统(ABS)是汽车制动主动安全性方面的重大技术成就之一,实际应用中控制方式主要是根据经验值确定逻辑门限值。为提高控制精度,许多学者对防抱死制动控制策略展开了研究,经典控制理论应用广泛。Andrei Aksjonov等[1]应用模糊逻辑控制器使电动车辆在各种路面下滑移率保持最佳状态,提高了车辆的安全性和能量经济性。Xiaoxiang Gong[2]提出了基于模糊控制器的防抱死制动方案,调节车轮滑移率,适应不同的制动强度。Rongxu Zhang等[3]采用PID控制算法和遗传优化PID控制算法对车辆稳定控制系统进行仿真研究,结果表明遗传优化PID算法具有更好的控制效果。Antonio Tota等[4-5]基于前馈和比例积分控制器设计了适用于传统ABS/电子稳定控制系统的制动卡钳压力控制器。凌滨等[6]将模糊控制算法与PID控制算法相结合,设计了基于滑移率的ABS控制器。Deliang Yu等[7]从汽车单轮动力学模型出发,利用改进的自适应滑模控制器实现对最优滑移率的有效控制。尹安东等[8]设计了基于最优滑移率滑模控制的电动汽车ABS控制策略,并运用遗传算法对滑模控制趋近律参数进行优化。上述研究均能达到车辆防抱死控制效果,但PID控制参数大多通过试凑法得到,难以适应各种工况,滑模控制开关不连续性造成的抖振难以消除。文中基于单轮动力学分析,设计了PID控制液压防抱死制动系统,通过粒子群优化算法(PSO)对PID参数进行整定,并在CarSim与MATLAB/Simulink中进行仿真试验,验证算法及控制策略的控制效果。
1 车辆制动动力学分析
1.1 单轮纵向动力学模型
车辆在制动过程中制动力主要受路面附着系数影响,不考虑垂向、俯仰和侧倾运动。假设车辆质量均匀分布,忽略非关键性因素如悬架、滚动阻力、空气阻力和路面不平度等的影响,将车辆简化为单轮模型,如图1所示。运用牛顿定律对单轮模型的纵向运动进行建模:

图1 单轮动力学模型
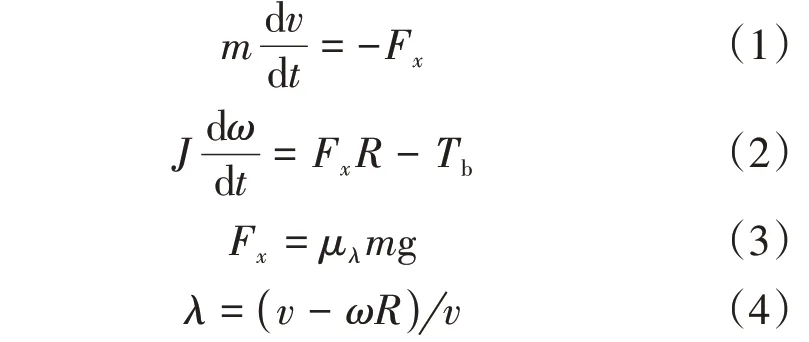
式中:m为整车1/4质量;v为汽车行驶车速;J为车轮转动惯量;ω为车轮角速度;R为轮胎半径;Tb为制动转矩;Fx为轮胎纵向力;μλ为路面纵向附着系数;λ为纵向滑移率。
1.2 轮胎与路面μ-λ模型
建立轮胎模型主要是建立车轮滑移率与路面附着系数之间的关系,便于选择CarSim试验验证中仿真路面以及对应路面理想滑移率值。相较于魔术轮胎公式较多的拟合参数,Burckhardt轮胎模型拟合参数较少,能够准确描述轮胎的特性,是非线性的轮胎经验模型,多用于描述轮胎的纵向摩擦特性,表达式如下[9]:

式中:c1、c2、c3为路面条件特征参数,根据路面状态不同其取值也不同,如表1所示。

表1 路面条件特征参数
不同路面条件下附着系数关于滑移率的函数图像如图2所示。由图2可知,在滑移率稳定区域内理想滑移率值对应的最大轮胎-路面附着系数,数学意义理解为该函数在一定的滑移率范围内具有极大值。对上述轮胎模型表达式应用极大值原理求得各路面理想滑移率表达式和最大轮胎-路面附着系数表达式如下:
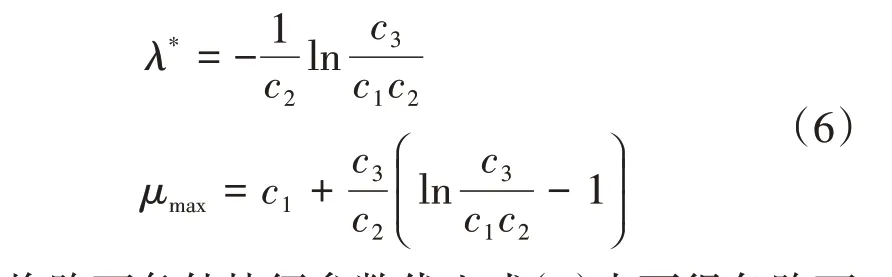
将路面条件特征参数代入式(6)中可得各路面理想滑移率和峰值附着系数,如表2所示。由图2及表2可知,6种不同路面条件下的车轮理想滑移率为6%~20%,6种典型路面划分为高中低附3类路面。高附着路面紧急制动工况中选择仿真路面附着系数μ为0.9,理想滑移率值λ*为0.2;中附着路面紧急制动工况中μ为0.4,λ*为0.15;低附着路面紧急制动工况中μ为0.2,λ*为0.09。
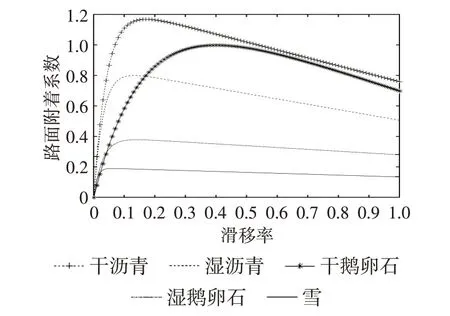
图2 滑移率与路面附着系数变化曲线
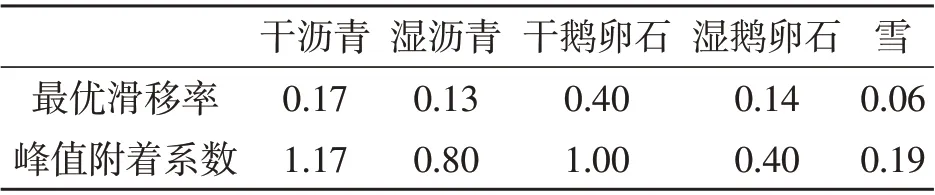
表2 不同路面的最优滑移率和峰值附着系数
1.3 液压制动系统模型
液压防抱死系统主要由液压制动力调节子系统与基本制动子系统组成。基本制动子系统通过缸内制动液产生压力保证制动进行,液压制动力调节子系统通过ABS控制器、轮速传感器以及执行器等对液压力进行调节,确保汽车在紧急制动时车轮不抱死并将滑移率控制在合理范围内。液压制动系统增压、保压、减压的动态压力调节模型为

式中:Pm为制动主缸压力,由CarSim车辆模型反馈;Pw为轮缸压力;ξ为压力调节信号,由PID控制器输出。制动压力传输系统和制动执行系统模型如下[10-12]:
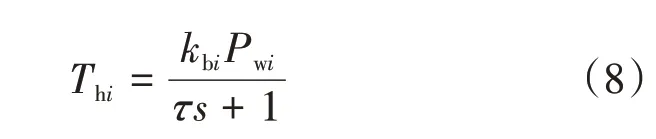
式中:kbi为制动因数;i为f表示前轮,i为r表示后轮;Thi为液压制动转矩;τ为液压系统滞后响应时间,由于电磁阀响应时间一般不大于10ms。
1.4 路面附着系数估计
为实现PID控制对全工况ABS的适用性,通过式(3)对路面附着系数进行粗略估计。

式中:Fz为轮胎垂直载荷。Fx和Fz由CarSim车辆模型反馈。根据表2以及CarSim路面模型对高中低路面附着范围进行划分,通过μλ判断车轮当前所处路面附着情况。路面附着系数估计模块确定路面情况后,切换控制模块根据高中低附路面选择相对应的λ*和压力调节控制模块。
2 基于PID控制的ABS模型
2.1 PID控制器
PID控制通过消除误差跟踪理想值进行控制,对模型要求不高,是设计控制系统中常用的控制方法。PID控制器是由比例控制、积分控制、微分控制组成的线性控制器,以理想值与实际值的偏差e(t)作为控制系统输入变量,控制规律如下:
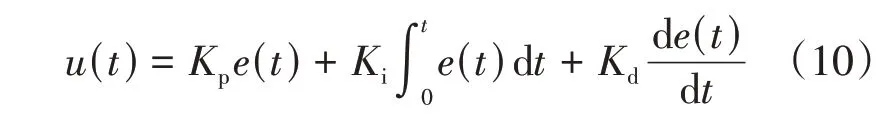
式中:Kp为比例系数;Ki为时间积分常数;Kd为微分时间常数。3个参数取值的合理性决定了PID控制器的性能。PID控制器的参数选取必须兼顾动态与静态性能指标要求,只有合理整定Kp、Ki、Kd,才能获得比较满意的控制性能。
将车轮理想滑移率作为控制目标,通过PID控制调节制动压力信号,保证制动过程中车轮滑移率始终保持在理想滑移率值附近。PID控制器输入为λ与λ*的误差,输出为制动压力调节信号,即
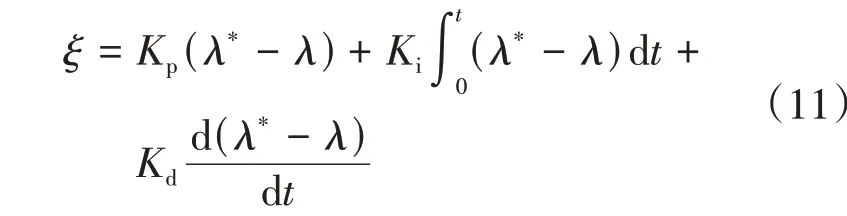
2.2 PID控制液压防抱死系统仿真试验
将CarSim仿真环境中建立的整车模型与MATLAB/Simulink建立的液压防抱死控制系统进行联合仿真,验证PID控制防抱死制动系统有效性。CarSim的输出变量为车速vx、4个车轮轮速vw、车辆制动主缸压力,输入变量为4个车轮的轮缸压力。PID控制液压防抱死系统联合仿真模型选用CarSim自带的B-Class Hatchback(No ABS)车辆,整车参数见表3。通过Carsim整车模型输出的车速和轮速变量计算出每个车轮制动过程中的实际滑移率,将λ与路面仿真工况对应λ*的误差作为PID控制器的输入,控制器输出制动压力调节信号。CarSim整车模型反馈的主缸压力信号与PID控制器输出的压力调节信号作为液压ABS制动系统的输入,系统输出轮缸压力反馈给整车模型。

表3 整车仿真参数表
CarSim整车模型中设定方向盘转角为0°,紧急制动动作0.2s时触发,车辆在1200m的直路面行驶。将CarSim整车模型中液压制动系统模块的ABS去掉,得到没有ABS控制系统的车辆模型具体仿真结果,如图3所示。由图3a可知,无ABS控制的车辆在紧急制动仿真动作触发后轮速迅速减小为0km·h-1,而车速在6s左右才减小至0km·h-1,这意味着车轮抱死拖滑。由图3b可知,车轮滑移率在制动开始后由0迅速增大至1。由图3可知,在紧急制动过程中无ABS控制的车辆会陷入车轮抱死拖滑的不稳定状态。

图3 无ABS控制系统仿真结果
高附着路面仿真工况下,设定4个车轮对应的μ均为0.9,设置λ*为0.2。PID参数通过试凑法取值,联合仿真试验结果如图4a~b所示。由图4a可知,0.2s车辆紧急制动开始,车速从120km·h-1减速至0km·h-1,制动时间约为3.3s。图4b中4个车轮的λ在理想值0.2 附近波动,始终保持在稳定区域内,保证了车辆紧急制动的安全性。
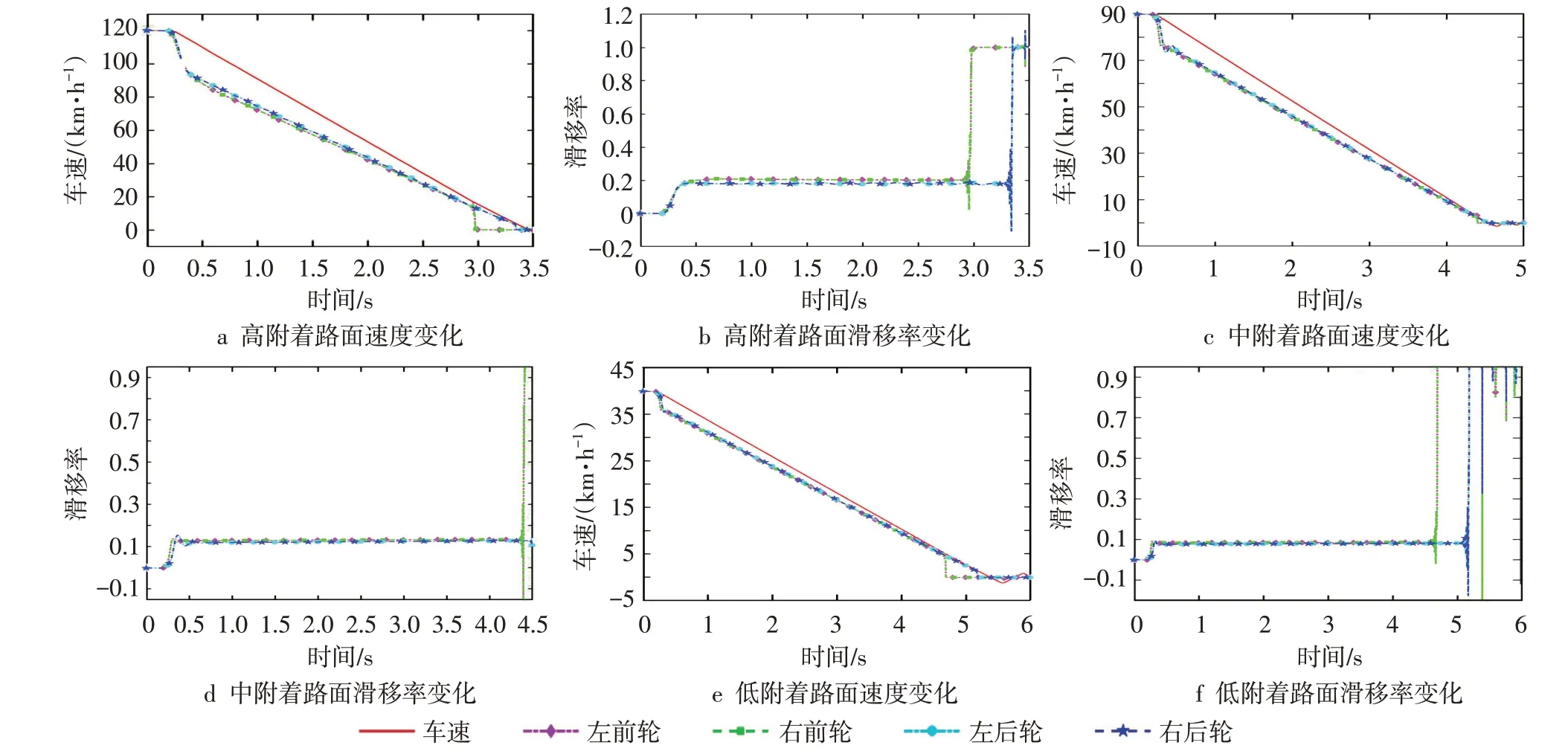
图4 附着路面PID控制液压防抱死系统仿真结果
中附着路面仿真工况下,CarSim中选择μ为0.5,根据表2,对应λ*为0.15,联合仿真结果如图4c~d所示。由图4c可知,仿真进行至0.2s触发紧急制动,在控制系统作用下,车速和轮速下降快而平顺,约4.7s后,车速从90km·h-1减小至0km·h-1,制动时间约为4.5s。由图4d可知,λ稳定在理想值0.15 左右,充分利用了路面纵向附着力。
低附着路面仿真工况下,CarSim中设置4个车轮对应的μ为0.2,根据表2,设定λ*为0.09,仿真结果如图4e~f所示。图4e中车速从40km·h-1减小至0km·h-1的时间约为5.3s。当速度降至5km·h-1左右时,车辆即将停车,允许车轮抱死,因此4.5s之后出现车轮先后抱死的状况。在PID跟踪控制的作用下,图4f中4个车轮的λ始终维持在0.1 左右,接近设定的λ*说明制动安全。
根据上述制动工况仿真结果可知,文中提出的PID控制液压防抱死系统能将车轮滑移率维持在理想值附近,充分利用地面附着力,紧急制动过程中保证车辆安全防止车轮抱死。
3 基于PSO的PID参数整定
3.1 粒子群优化算法
文中采用PID控制器,通过调整车辆制动过程中的制动压力达到紧急制动安全停车的目的,PID参数的取值直接影响控制效果。对输出至4个车轮的轮缸压力进行控制,相当于要对4个控制器参数进行整定,每当路面工况改变时,为达到较好的控制效果,PID控制器参数都需重新试凑,增大了PID控制防抱死系统的工程应用难度。因此引入PSO与PID控制的Simulink模型进行参数整定。根据CarSim中整车模型反馈的车轮状态数据可知,车辆2个前轮的运动状态基本一致,2个后轮的运动状态也几乎一样。因此整车模型可简化为前后半车模型,即对1个前轮控制器和1个后轮控制器的控制参数进行整定。
粒子是由前后车轮的2个PID控制器参数组成的6维向量,算法产生粒子群并通过调用m文件中的函数赋值给MATLAB工作空间,之后Simulink模型中参数Kpf、Kif、Kdf、Kpr、Kir、Kdr获取工作空间的值,完成粒子从m文件到仿真模型的传递。优化设计过程如图5所示。
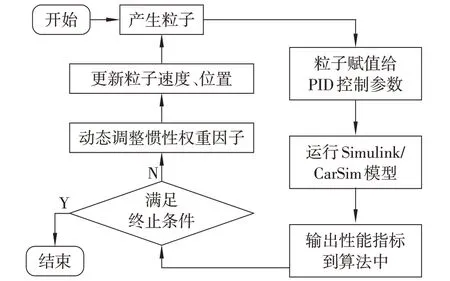
图5 PSO整定PID参数流程图
为避免算法陷入次优解,选取动态调整惯性权重因子,在算法搜索初期wstart赋以较大值,在求解后期设定wend较小值:
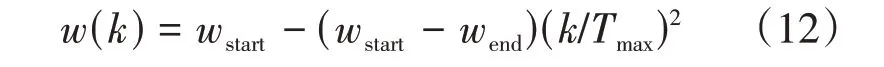
式中:k为当前迭代次数;Tmax为迭代次数。
3.2 PSO整定PID控制仿真试验
3.2.1 粒子群参数对整定效果的影响
PSO整定PID的试验中,粒子群参数不同整定效果也不同。文中只展示μ为0.5 的中附着路面仿真结果。图6为采用不同惯性权重和不同加速因子进行算法整定的速度控制结果图。由图6a~b可知,加速因子c1为1.9 、c2为1.5 的算法整定控制的制动时间为10.5s左右,c1、c2均为1.9 的算法整定控制的制动时间为8.2s左右。因此相同加速因子的PSO整定后制动时间更短。由图6b~c可知,动态惯性权重与定常惯性权重算法整定的制动时间差不多,图6b中动态调整惯性权重整定控制的轮速超调更小。
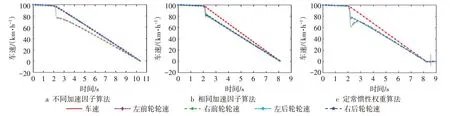
图6 不同粒子群参数的整定速度曲线
根据上述分析,确定PSO惯性因子wstart为0.8,wend为0.4;c1为1.9,c2为1.9。选取控制性能指标:

由于需整定2个控制器参数,有2个输入误差,因此性能指标为
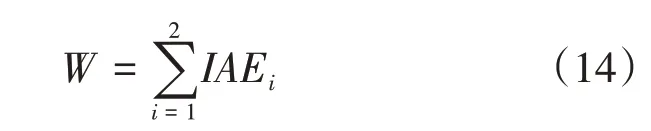
将PSO整定的PID参数构建控制参数表,赋值给PID控制器,采用切换控制并根据路面附着系数选择对应的控制器。对PSO与CarSim-Simulink联合仿真模型进行试验,仿真条件设置与PID控制仿真验证相同。
3.2.2 附着路面仿真测试
车辆在μ为0.9 的高附着路面紧急制动,粒子群优化算法迭代第10次时收敛,PSO整定的PID控制器参数如下:前轮Kpf为12.3455 、Kif为9.903 、Kdf为0.7627,后轮Kpr为19.1389 、Kir为0.9505 、Kdr为0.7276。高附着路面仿真结果如图7a~b所示:车辆在0.2s时以120km·h-1的速度紧急制动,在3.5s左右减小至0km·h-1,整个制动过程大概花了3.3s,制动时间较短。图7a中,当速度降至10km·h-1以下时,车轮低速抱死,随后0.5s内完全停车,不影响制动安全。如图7b所示,制动过程中4个车轮的λ在控制器作用下均稳定在0.17~0.2 的理想范围内,较好地利用了路面附着条件。
车辆在μ为0.5 的中附着路面紧急制动,粒子群算法整定控制器参数在迭代到第7次时收敛,PSO整定PID控制器参数如下:前轮Kpf为1.4710、Kif为9.5969、Kdf为0.7866;后轮:Kpr为16.7871,Kir为2.6412,Kdr为0.4239。中附着路面速度变化仿真结果如图7c所示:0.2s时紧急制动仿真动作触发,大约在4.7s时,速度从90km·h-1减小至0km·h-1,制动时间约为4.5s。图7d中车轮滑移率在短暂波动之后一直维持在理想值0.15 附近,控制目标值跟踪效果较好,控制精确度较高。
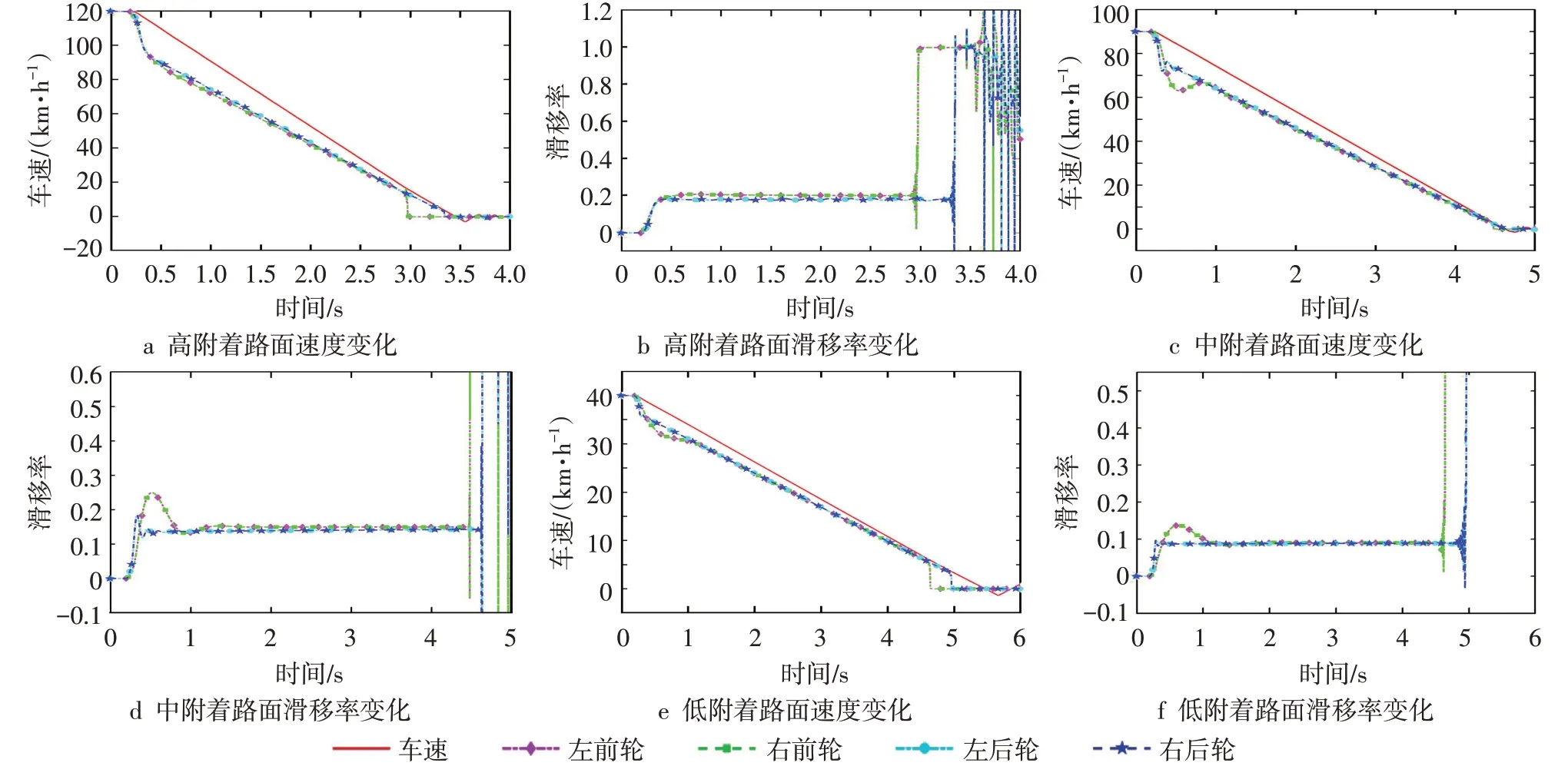
图7 紧急制动仿真测试结果
在μ为0.2 的低附着路面上,PSO算法整定PID控制器参数如下:前轮Kpf为18.8833 、Kif为8.0933 、Kdf为0.2968,后轮Kpr为17.8063 、Kir为4.3937 、Kdr为0.1927。图7e中,车辆在0.2s紧急制动,在5.5s左右车速从40km·h-1减小至0km·h-1,图7f中滑移率稳定在0.09 的理想值附近。车速降到5km·h-1以下时,前轮开始抱死,经过了0.3s之后后轮开始抱死,这种情况一般不会发生后轴侧滑,且如果车轮是低速抱死也不会导致车辆失去转向能力[13]。
3.2.3 对接路面仿真测试
对接路面仿真条件设置如下:制动初始行驶在μ为0.2 的低附着路面,180m处对接的μ为0.6。由图8a可知,对接路面上轮速在路面工况改变的瞬间产生波动,但很快趋于平稳,且车轮没有出现提前抱死的不稳定状态。图8b中,低附着路段滑移率控制在0.05~0.1,中附着路段滑移率控制在0.1~0.15。仿真结果表明,通过路面附着估计实现理想滑移率与对应PID控制器选择的方法是可行的。
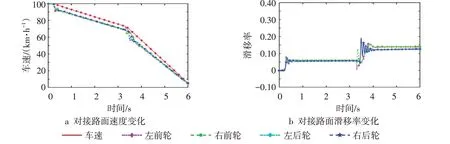
图8 对接路面紧急制动仿真测试结果
4 结论
考虑PID控制参数试凑难以满足液压防抱死系统工程应用,文中提出采用粒子群优化算法整定PID控制参数,并通过路面识别模块实现控制参数切换满足ABS实时性要求。通过高中低附着路面以及对接路面的联合仿真试验,验证了粒子群优化算法整定参数的PID控制液压防抱死系统,能够在紧急制动时避免车轮抱死,达到安全制动。

