一类实矩阵对广义奇异值的表达公式

沈卫杰, 汤天宇, 徐玮玮

(南京信息工程大学数学与统计学院, 南京 210044)

特征值和奇异值在数值计算领域中有着重要的应用[1]. 矩阵对的广义奇异值分解(Genera-lized Singular Value Decomposition,GSVD)已成为许多实际应用中重要的计算方法[2-8]. 近年来,学者们对大规模数据矩阵中的GSVD进行了大量研究,如:ZHANG等[5]应用神经动力学网络开发了一种用于求解GSVD的近似值的神经网络模型;WEI 等[6]使用随机投影捕获矩阵行为,提出一种用于计算 GSVD 的低秩逼近的随机算法;刘圆圆[7]引入随机方法,提出了一种改进的GSVD方法,将其用于求解具有一般形式的大规模线性离散病态问题；XU等[9-10]研究了一类酉约束矩阵优化问题的解析解.

受文献[9-10]启发,本文将利用迹函数的矩阵优化问题来计算实矩阵对的广义奇异值,提出计算一类实矩阵对的任意广义奇异值的新公式,并用数值算例来验证本文结论的有效性.

1 预备知识

下面给出一些基本定义和定理.

定义1[11]若Am×n,Bp×n,有rank(AT,BT)=n,则称矩阵对{A,B}是(m,p,n)实矩阵对.

定义2[11]若(α,β)≠(0,0),det(β2ATA-α2BTB)=0,α,β≥0,则称(α,β)是实矩阵对{A,B}的广义奇异值. {A,B}的广义奇异值(α,β)的集合记作σ{A,B}.

定理1[12]若{A,B}是一个(m,p,n)实矩阵对,则存在正交矩阵Um×m和Vp×p以及非奇异矩阵Wn×n,使得

UTAW-1=ΣA,VTBW-1=ΣB,

(1)

(2)

其中,

Λ=diag(α1,…,αr+s),Ω=diag(βr+1,…,βn),

1=α1=…=αr>αr+1≥…≥αr+s>αr+s+1=…=αn=0,

0=β1=…=βr<βr+1≤…≤βr+s<βr+s+1=…=βn=1,

定义3[13]设A=(aij)n×n,如果对所有的i,j都有aij≥0,则称A是非负矩阵.

定义4[13]设A=(aij)n×n是非负矩阵,如果A满足

则称A为双随机矩阵.

2 主要结论

本节将通过迹函数的优化问题给出一类实矩阵对广义奇异值的表达公式. 首先,给出一些必要的引理.

引理1[14]如果D=(dij)是一个n阶双随机矩阵,并且

x1≥…≥xn≥0,y1≥…≥yn≥0,

则

引理2令Γ=diag(γ1,…,γn)和Δ=diag(δ1,…,δn)是n×n上的2个对角矩阵,γ1≥…≥γn≥0,δ1≥…≥δn≥0,则

证明令Φ*=In,则

另一方面,因为tr(AB)=tr(BA),有

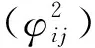
证毕.

由引理2可得以下推论.

推论1令Γ=diag(γ1,…,γn)和Δ=diag(δ1,…,δn)是n×n上的2个对角矩阵,0≤γ1≤…≤γn,0≤δ1≤…≤δn,则

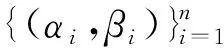
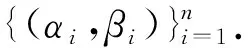
(3)

其中,

Qi=diag(Ii,O(n-i)×(n-i)).

(4)

证明令{A,B}是由式(1)和式(2)定义的(n,n,n)实矩阵对,则有

进一步地,有

(UTAW-1)T(UTAW-1)+(VTBW-1)T(VTBW-1)=In,

化简得

ATA+BTB=WTW.

对任意的1≤i≤n,令Qi由式(4)定义.因为tr(AB)=tr(BA),则由引理2,可得

类似地,

因此,式(3)得证. 证毕.

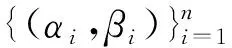
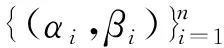
3 数值算例

本节给出一些数值算例来验证定理2的有效性.

例1设

利用MATLAB R2020a的命令 gsvd,可以得到实矩阵对{A,B}的广义奇异值为

σ{A,B}={(αi,βi)}={(0.993,0.115),(0.877,0.480),

(0.606,0.795),(0.149,0.989)}.

应用引理2,记H=A(ATA+BTB)-1AT, 有

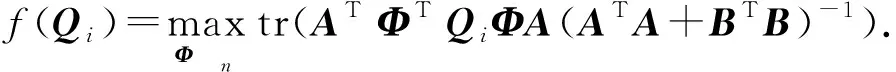
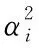
表1 已知实矩阵对{A,B}计算的和 f(Qi)-f(Qi-1)

例2设n=100. 使用MATLAB R2020a中的命令 rand,随机生成满足

1=α1=…=αr>αr+1≥…≥αr+s>αr+s+1=…=αn=0,

0=β1=…=βr<βr+1≤…≤βr+s<βr+s+1=…=βn=1

和

表2 广义奇异值Table 2 The generalized singular values

于是,实矩阵对{A,B}有广义奇异值分解

A=Udiag(α1,…,αn)W,B=Vdiag(β1,…,βn)W,

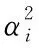
表3 已知广义奇异值计算的和 f(Qi)- f(Qi-1)