涡桨飞机缩比模型机体噪声预测研究

宋敏华, 宋文萍, 王跃, 韩忠华, 张彦军, 雷武涛

1．西北工业大学翼型、叶栅空气动力学重点实验室气动与多学科优化设计研究所， 陕西西安 710072；2．中国航空研究院， 北京 100029； 3．航空工业第一飞机设计研究院， 陕西西安 710089

飞机的气动噪声会对机体结构和机场附近人员的健康带来严重的负面影响，与客机设计所要求的“四性”严重相悖，噪声水平是民机设计的关键问题之一。从2018年1月1日起，飞机噪声第五阶段控制标准正式生效，这将在第四阶段的标准上进一步降低7 dB。越来越严苛的适航条例使得噪声水平成为影响民机能否取得适航证的关键因素之一，这对于我国正在研制的新一代民用涡桨客机和大型客机来说无疑是一项巨大的挑战。因此，对飞机的噪声进行预测，深入了解其机理并进行降噪具有十分重要的意义。

机体噪声是飞机噪声的重要组成部分[1]，为了研究飞机机体噪声机理并发展降噪技术，从20世纪70年代开始，NASA启动飞机噪声预测项目(ANOPP)对飞机各部件的噪声进行预测，发展了部件级的半经验噪声预测工具[2]。在随后的数十年间，美国和欧洲在持续的大型项目支持下，对气动噪声进行了深入的数值模拟及实验研究。当前针对飞机远场噪声的预测，主要还是采用结合CFD和声类比的混合方法，随着计算能力的发展，混合方法中针对声源模拟的CFD方法也从工程常用的雷诺平均Navier-Stokes(RANS)方法[3]变成更高精度的混合RANS/LES方法[4]，甚至是大涡模拟方法(LES)[5]或直接数值模拟方法(DNS)[6]。经过多年的研究，结合高精度CFD的声类比方法在孤立部件的气动噪声预测上已经取得了非常显著的成果。

近些年来，得益于计算能力的进一步提高，国外一些研究机构开始针对全机复杂构型进行气动噪声研究，并进行风洞实验和飞行试验验证。NASA在对环境负责的航空(ERA)项目的支持下，和Gulfstream合作对短程小型客机的气动噪声进行了深入的研究。在2014年，NASA对缩比18%的高保真全机半模构型(包括机身、机翼、襟翼、平尾和垂尾以及通气短舱等)在降落状态下的非定常流动及噪声进行了大量的数值模拟[7]。表面探测点的压力分布、非定常脉动的频谱和远场的噪声预测结果,均与风洞实验均吻合较好。在起落架收起和放下2种状态下，远场噪声的频谱在8 000 Hz以内计算结果和实验值分别相差约1 dB和2 dB。在2016年，研究者将缩比模型半模噪声预测研究拓展到全尺寸全模，提高了预测的雷诺数和飞机几何的复杂度，并将数值模拟结果和2006年的飞行试验结果进行了对比[8]。研究结果表明，在中低频段全尺寸和缩比模型计算得到的结果和实验值基本一致。但同时也表明，襟翼支架等机构对远场的中高频噪声有较大的贡献。2018年通过对真实飞机进行激光扫描，实现了更高几何保真度构型的气动噪声数值模拟[9]。目前，NASA计划将在短程支线客机的气动噪声数值模拟方面获得的丰富经验应用于完整的全尺寸双通道大型民机，并已经在波音777-200的26%缩比起落架上开展了初步的研究[10]。结果表明，数值模拟和实验的波束成型积分结果在9 000 Hz的范围内，频谱的结果都吻合较好。除美国之外，日本从2015年开始了针对机体噪声的研究与降噪项目FQUROH[11-12]，同时采用数值方法、风洞实验和飞行试验的方法对典型客机的机体噪声和一些降噪方案进行了深入的研究。

国内在机体噪声领域的研究开展得相对较晚，但也取得了许多突出的成果。在增升装置噪声预测方面，张宇飞等[13]采用壁面模化LES(WMLES)方法，以30P30N多段翼型为例，对增升装置的噪声进行了深入研究。通过对定常流场、瞬态流场、表面压力频谱、远场噪声的频谱、指向性以及速度率等方面的深入研究，对噪声机理进行了比较详细的分析。龙双丽等[14]采用结合基于SA模型的DES方法和FW-H方法，研究了起落架近场的非定常流动、噪声的产生机制和主要的噪声源位置、频谱特性及远场指向特性，并评估了各部件对总噪声的贡献量，同时还开展了起落架风洞实验研究并将数值模拟结果和实验值进行了对比。肖志祥等[15]采用基于SST模型的延迟分离涡模拟方法(DDES)和改进的延迟分离涡模拟方法(IDDES)对起落架噪声进行了数值模拟研究。除此之外，国内还有很多针对飞机机体噪声的研究，在此不再赘述。

但是，当前国内针对飞机气动噪声和降噪方法的研究基本都局限于飞机的部件，而且其中许多是对标准算例进行研究，着重强调各个单独噪声源的预测及其特性，而忽略了部件之间干扰而产生的噪声，而有时候后者的噪声强度和熟知的单独噪声源的强度相当，而且对全机的噪声强度和指向性等均有显著影响。此外，噪声特性预测和气动特性预测不同，较小的几何部件也可能对全机的噪声产生较大的影响，因此对更加真实的包含更多几何细节的全机复杂构型进行噪声预测研究十分必要。

因此，本文采用精细化的高分辨率网格、高精度的IDDES湍流模拟方法对涡桨飞机高保真模型在降落状态的1/6缩比构型进行气动噪声预测研究，从而更全面地认识全机的气动噪声特性，为我国自主研制的涡桨飞机提供更全面的气动噪声特性分析，缩短与国外的差距。

1 数值方法

1.1 非定常流场求解方法

本文采用有限体积法求解非定常NS方程，采用的积分形式控制方程为

(1)

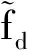
(2)

LES和RANS长度尺度分别为

(3)

式中

ΔIDDES=min(max[Cwdw,Cwhmax,hwn],hmax)

(4)

为重新定义的亚格子尺度,hmax是网格在3个方向上的最大网格尺度,hwn为沿壁面法向网格单元尺度,dw是网格单元与壁面的距离。通过使用IDDES方法,既可以使用DDES模式,又可以用壁面模化LES模式,2种模式的选择通过混合函数实现

(5)

式中,fdt为保护函数

fdt=1-tanh[(20rdt)3]

(6)

式中

(7)

fB为该模型的另一个混合函数,其表达式为

fB=min[2exp(-9α2),1]

(8)

控制方程的对流项离散采用迎风AUSM格式,通量计算采用3阶MUSCL插值,黏性项采用中心格式离散。时间离散采用双时间步方法,同时在内迭代中采用预处理和多重网格方法加速收敛。物面采用无滑移绝热壁面边界条件,远场添加吸收边界以减少边界的反射,避免对计算结果的污染。NASA在针对飞机全机噪声预测研究中发现,飞机全机的左右两侧声源相干性弱,全模的噪声频谱相对于半模在整个频谱范围内都增加3 dB左右,可以通过半模的噪声预测结果得到全机的噪声特性[9]。因此,本文对飞机的半模进行噪声预测,对称面采用对称边界条件。无限展长算例的展向也采用对称边界。

1.2 远场噪声计算方法

本文的远场噪声求解采用基于FW-H方程的声类比方法[17],FW-H方程同时考虑了固壁及固壁的运动。声类比方法将噪声预测分为两部分——噪声的产生和噪声的传播。在近场,流体运动十分复杂,存在强烈的非线性,直接采用CFD方法求解声源。在远场,假设近场产生的噪声在均匀介质中传播,采用解析的方法求解远场噪声。FW-H方程为

(9)

式中

(10)

Tij为Lighthill应力张量；c0为远场声速；ui是xi方向的流体速度分量；vn是固壁的法向速度分量；δ(f)为Dirac函数；δ(f)=∂H/∂f,H(f)为Heaviside函数。FW-H方程右端3项分别代表单极子声源项、偶极子声源项和四极子声源项。本文研究飞机降落状态时的噪声,来流速度低,空间四极子噪声在全部噪声源中的占比很小,因此本文直接采用固壁作为声源面进行积分求解远场噪声。本文采用的积分方法为Farassat等提出的时域方法[18]。厚度噪声和载荷噪声的表达式如下:

(11)

2 算例验证

30P30N是研究增升装置气动噪声广泛采用的多段翼构型。该翼型由前缘缝翼、主翼和后缘襟翼三部分组成,模型的弦长C为0.457 2 m,来流马赫数为0.17,基于弦长的雷诺数为1.71×106。计算采用多块结构网格,计算网格如图1所示,展向长度取1/9C[19]。网格沿展向拉伸45层,网格量约为1 800万。

计算的来流迎角α=5.5°,非定常计算物理时间步长为0.000 6C/U∞,内迭代5步。图2是时均压力分布的计算结果和日本宇航局(JAXA)的实验结果[20]对比,可以看到,翼型各段的表面压力分布都和实验值十分吻合。

图1 30P30N多段翼型计算网格

图2 压力分布与实验值的对比

在缝翼区域,速度分布的预测结果和弗洛里达州立大学(FSU)的PIV实验结果[21]对比如图3所示,在缝翼凹腔内两者的速度分布基本吻合。从缝翼前缘尖端脱落的剪切层及其失稳是这个部位的重要流动特征,准确捕捉剪切层对预测该翼型的气动性能及气动噪声非常重要。对图3所示沿剪切层发展方向的7个剖面位置处速度型的计算和实验结果进行了对比,剪切层的速度型预测结果和实验基本一致。由于篇幅所限,图4只给出L2和L6剖面的对比图。可以看到剪切层的速度型预测结果和实验基本一致。

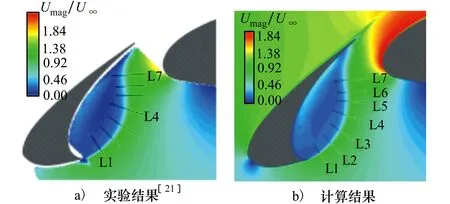
图3 缝翼区域速度大小对比

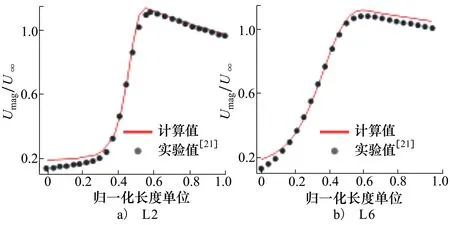
图4 缝翼剪切层剖面速度型对比

计算得到的翼型表面部分压力脉动频谱和实验值对比如图5所示,其中P3位于缝翼凹腔内，P6位于缝翼的上表面后缘，横纵坐标分别为斯特劳哈尔数和归一化功率谱密度

式中：GPP为压力脉动的功率谱密度；U∞为远场来流速度；s和q分别是缝翼弦长和远场来流的动压。数值模拟准确地捕捉到了单音噪声的频率,和实验值基本吻合,在中低频部分,频谱幅值和实验值吻合较好,高频部分比实验值偏低。

图5 表面探测点压力脉动频谱和实验值对比

为了验证声类比方法计算远场噪声的准确性,采用FW-H方法,对远场的噪声结果进行验证。远场观测点的位置分为2组,分别是JAXA[22]和FSU[23]的实验结果。JAXA的观测点位置位于10倍弦长处,角度分别为沿流向逆时针的249°,270°和291°,FSU观测点位于2.19倍弦长处,角度为287.5°,所有观测点都大致位于翼型的下方。其中FSU的数据包括采用波束成型积分和单独麦克风信号的实验结果,实验的模型展向方向是1 m,因此将计算结果归一化为展向方向1 m并进行对比。2组观测点的计算结果和实验值对比如图6所示,可以看出,在6 000 Hz以内,频谱的计算结果和实验值吻合较好。

图6 远场噪声频谱和实验值对比

从上述结果来看,本文采用的数值模拟方法对30P30N翼型的气动特性及气动噪声都进行了准确的预测,结果和实验值基本一致,验证了该方法在气动及气动噪声预测上的准确性。

3 涡桨飞机气动噪声模拟

3.1 计算模型和网格

采用上述数值方法,对涡桨飞机降落状态下的气动噪声进行模拟。飞机全机外形半模如图7所示,由机身、增升装置(主翼、翼尖小翼、襟翼舱与襟翼)、发动机短舱等部分组成,襟翼偏角38°。纵向对称面为XZ平面,X方向沿机体水平向后,Y方向为展向。在本文的研究中,不考虑发动机内部的流动,对进气道入口进行了封闭,计算采用缩比为1/6的半模实验模型。

图7 降落状态几何模型

生成1套高质量的计算网格对气动噪声的模拟十分重要。本文采用混合网格,即物面附近采用三棱柱或六面体网格,其余采用四棱锥或四面体网格。首先进行物面网格的生成,在物面的大部分区域,采用结构网格的生成方法。生成的表面网格为35万,其中四边形网格31万,三角形网格4万,物面网格如图8所示。

图8 全机半模构型表面网格

在生成了表面网格之后进行体网格的生成。为了尽可能提高边界层内和边界层外的模拟精度,需要物面附近的棱柱形网格有一定的层数,同时需要附面层外各向同性网格的尺度不会因为物面法向的各向异性网格层数过多而过大。另外,也要避免在一些狭缝位置,附面层网格层数过多导致网格过渡急剧变差,如襟翼和机翼的后缘、下方的襟翼舱端板之间。针对该构型,边界层内的棱柱形网格最小层数为25层,大部分区域为40层左右,为了提高附面层的模拟精度,第一层网格高度为5×10-6m,预估的y+略小于1。为了提高噪声源的模拟精度,附面层的增长率较小,各向异性网格的增长率为1.13。

在网格生成过程中,对襟翼内侧和外侧侧缘、增升装置尾迹区、翼尖等几个可能的重要噪声源部分的网格均作了仔细处理。声类比方法的噪声求解精度很大程度上取决于声源的准确模拟,所以在这几个可能的重要噪声源位置,通过限制其附近的网格尺度来提高对流动细节的捕捉,从而提高声源的模拟精度。为了和验证算例保持一致,针对全机构型噪声研究的网格在近壁面区域和多段翼型的网格尺寸相当,在增升装置内侧和机身相接的部位、襟翼外侧侧缘以及翼尖等潜在的重要噪声源区域,网格尺寸在0.1%弦长左右。另外,缩比的全机模型和多段翼型的平均气动弦长和雷诺数差别不大,因此,预计2套网格所能捕捉的频率范围也基本相同。最终生成的空间网格总量约为1.03亿。其中,六面体网格2 100万,四面体网格7 800万,四棱锥网格170万,三棱柱网格300万。沿流向和展向的2个剖面处的网格分布如图9所示,可以看出,在物面附近的声源区域,网格进行了明显加密。

图9 模型附近的网格加密

3.2 全机气动特性与气动噪声预测

计算状态为Ma=0.2,Re=1.9×106。来流迎角α=6°。非定常计算内迭代5步。计算环境为天津超算中心HPC1系统,处理器型号为Intel Xeon CPU E5-2690 v4@2.60GHz,采用8个节点并行计算,每个节点为28核。计算模拟的物理时间约为0.16 s,所耗费的计算资源约为1.6×105核时。计算过程中气动力系数变化如图10所示,升阻力系数都逐渐收敛于一个稳定的值。

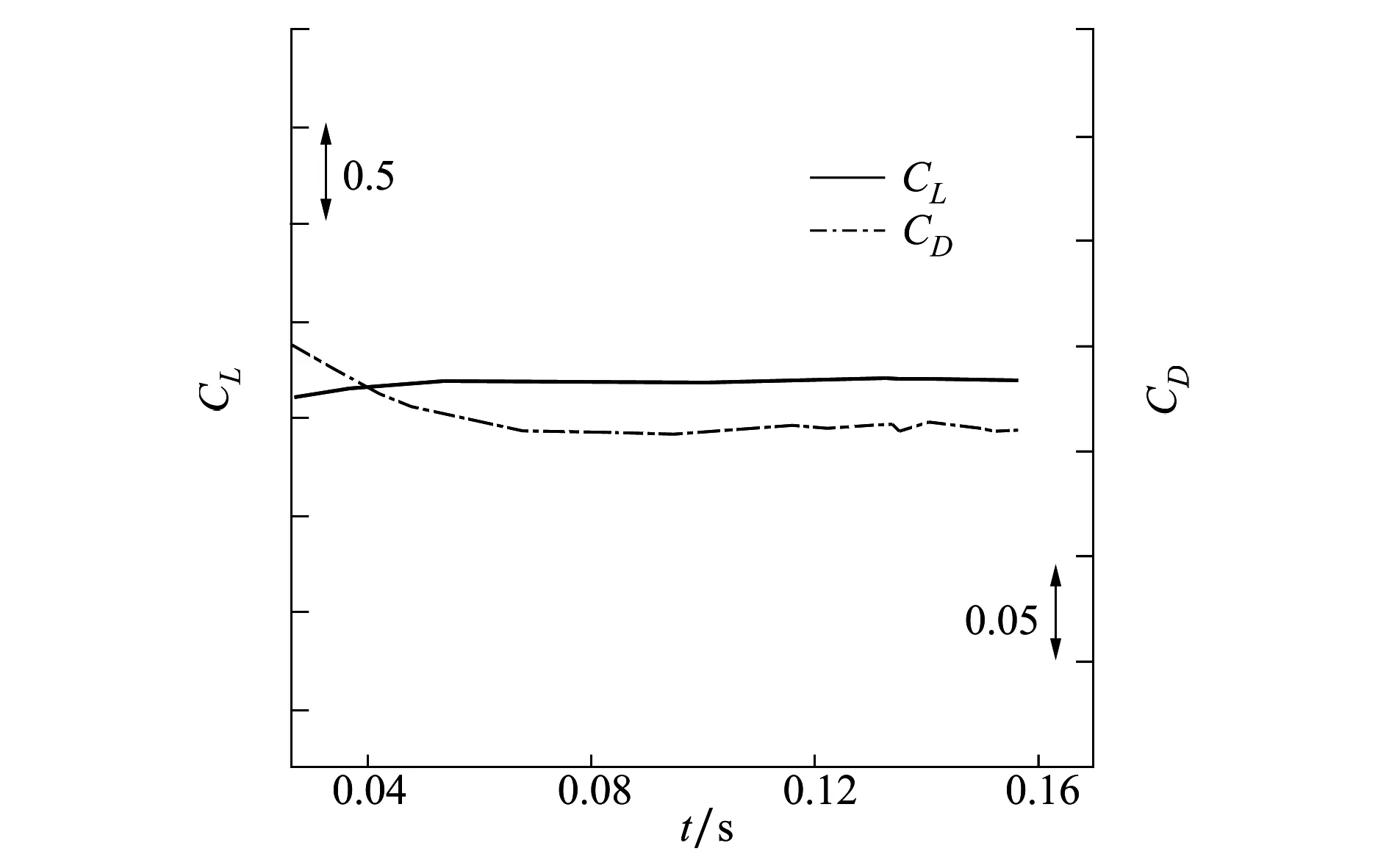
图10 气动力系数收敛情况

图11 无量纲螺旋度染色的Q判据等值面(Q=10 000)

图12是全机在流向截面(X=2.6 m)的瞬态密度波动,截面的位置大概在襟翼的中弦线处。该二维切面清楚地显示了声波的产生和在空间中的传播。可以明显地看到,襟翼的外侧侧缘和翼尖是声源的重要区域,而且襟翼的噪声更强。除了这两个单独部件产生的噪声之外,短舱的尾迹和襟翼之间、襟翼内侧和机身之间的干扰产生了非常复杂的流动,引起了强烈的声压脉动,其幅值甚至高于襟翼侧缘和翼尖,是全机构型重要的噪声源,由此可以看出全机构型噪声预测的必要性。

图12 流向方向(X=2.6 m) 瞬时脉动密度云图

全机表面的压强脉动如图13所示,可以清楚地看到这几个噪声源区域产生的噪声在机体表面的传播。

全机表面的压强均方根如图14所示,在襟翼内侧和机身相邻部分、短舱后方的襟翼、襟翼外侧侧缘及翼尖几个部位,压强的均方根显著高于其他部位。在和机身相邻的襟翼内侧,发展出的复杂涡流沿流向方向发展,和机身之间相互作用,产生了强烈的压力脉动,诱导偶极子噪声,涡和机身之间的干扰也是重要的噪声源。

机体表面及襟翼侧缘附近的展向截面处的瞬时脉动密度如图15所示。可以看出,展向截面的压力脉动主要由襟翼的侧缘产生。在襟翼的尾迹区,湍流脉动产生的噪声频率较高但幅值较小。相对于襟翼的后缘噪声,襟翼的侧缘噪声更强。

图13 表面压力脉动云图 图14 表面压力均方根分布图15 机体表面及襟翼侧缘附近展向截面的瞬时脉动密度

下面对远场噪声及其指向性进行研究。远场噪声观测点分为2组,即WBA201-WBA272和WBA301-WBA372,分别位于垂直来流的平面和机体纵向对称面。圆心均为气动中心,半径均为7 m,每隔5°布置一个观测点。部分观测点的声压频谱(参考压力2×10-5Pa)分别如图16～17所示。

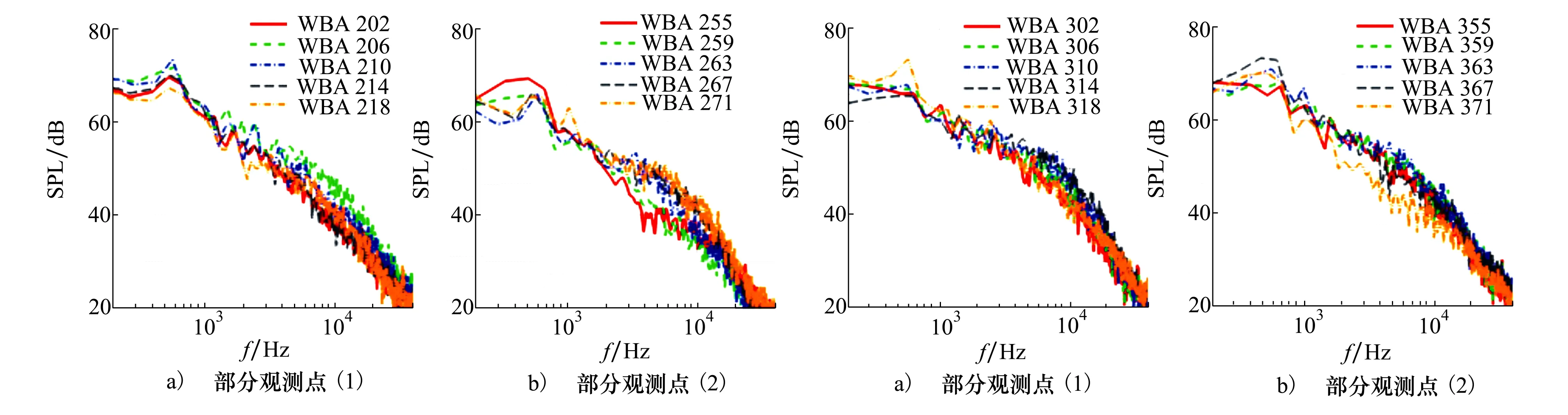
图16 WBA201-WBA272部分观测点噪声频谱 图17 WBA301-WBA372部分观测点噪声频谱

图18和图19分别为2组观测点的总声压级。

图18 垂直流向平面(YZ平面)指向性

图19 纵向对称面内(XZ平面)指向性

在垂直于流向的YZ平面，横向的噪声更小，侧下方和侧上方的噪声更强。在机体的纵向对称面内(XZ平面)，噪声主要向前下方和后上方传播，噪声呈现明显的偶极子特性。

4 结 论

本文采用基于SST模型的IDDES方法，对涡桨飞机的1/6缩比模型进行了气动噪声研究。近场高精度CFD方法对声源区的流动进行了精细地模拟，捕捉到了近场区域噪声的产生和传播。研究结果表明，襟翼外侧侧缘、翼尖、短舱的尾迹和后缘襟翼之间的干扰以及襟翼和机身之间的复杂流动是该构型最重要的噪声源。远场噪声研究结果显示，噪声主要向前下方和后上方传播，偶极子特性十分明显，水平横向噪声相对更弱。对于涡桨飞机来说，螺旋桨也是重要的噪声源，而且增升装置的一些辅助部件对气动噪声也有一定的影响，因此下一步计划对包含这些部件的更复杂的全机模型噪声进行更加深入的研究。

致谢本文工作是在国家超级计算天津中心的“天河一号”超级计算机上完成，感谢“天河一号”的大力支持。