时速400 km高速铁路接触网系统参数研究

陈 伟

0 引言

中国高速铁路经过多年的发展，从京津城际铁路到陆续开通运营的郑西、武广、哈大、京沪、津秦、京石武等高速铁路，已经形成了成熟的技术体系[1]。目前，我国已经形成了200 km/h以下、200～250、300～350 km/h不同速度等级的接触网系统标准体系，而设计速度400 km/h的高速铁路在国内尚无先例。当前，高速铁路面临“走出去”的大好机遇，俄罗斯、英国等国家均提出进一步提速至400 km/h的需求[2]。因此，开展时速400 km高速铁路接触网系统参数方案研究，可以为确保接触网系统的平稳受流和安全可靠性，为中国标准高速铁路接触网及中国高铁“走出去”提供技术支撑。

本文首先提出时速400 km接触网系统参数评价标准，之后利用接触网仿真软件通过对比张力、跨距等关键因素对接触线波动传播速度、接触力、离线率等系统评价指标的影响，提出适合于400 km/h速度等级的接触网系统参数，实现技术经济性能最优。

1 400 km/h接触网系统参数评价标准

由于目前国内尚无400 km/h等级接触网系统参数评价标准，在对400 km/h接触网系统参数配置进行静动态性能分析之前，需建立与之匹配的评价标准。

1.1 静态弹性不均匀度

《高速铁路设计规范》（TB 10621—2014）中11.5.2.4条规定：弹性链形悬挂的弹性不均匀度不应大于10%，简单链形悬挂的弹性不均匀度不宜大于25%[3]。时速400 km等级接触网弹性不均匀度标准可参照执行。

1.2 弓网接触力标准偏差

弓网接触力标准偏差是影响弓网受流质量的重要因素，大量测试数据表明，弓网接触力测量结果的概率分布符合正态分布规律，标准偏差越小表明弓网接触力的离散性越小，弓网系统运行越平稳[4，5]。接触力标准偏差可根据平均接触力进行计算：

式中：δ为接触力标准偏差，N；Fm为平均接触力，N。而平均接触力Fm和运行速度v（km/h）有关，具体可通过下式计算：

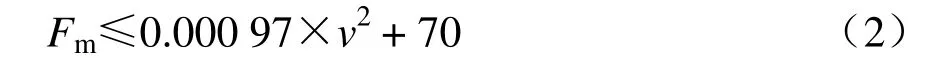
对于时速400 km等级高速铁路接触网，最小接触力和最大接触力参照《高速铁路设计规范》（TB 10621—2014）条文说明执行。相关动态接触力标准如表1所示。

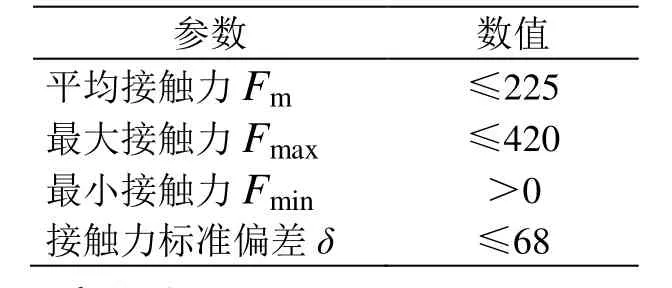
表1 动态接触力标准 N

1.3 弓网离线率

弓网离线率是影响接触网受流质量的关键指标[6]，《高速铁路设计规范》（TB 10621—2014）中对离线率要求为不大于1%，针对400 km/h速度等级接触网的离线率标准可参照执行。

1.4 接触线波动传播速度

接触线波动传播速度与弓网受流质量息息相关，同时也是接触网设计的关键控制参数[7]。波动传播速度m与接触线张力相关，具体可通过下式计算：

式中：gj为接触线单位质量，kg/m；Tj为接触线工作张力，kN。《高速铁路设计规范》（TB 10621—2014）中要求设计最高行车速度与接触线波动传播速度之比不应大于0.7。时速400 km接触网的波动传播速度标准可参照执行。

1.5 反射因数

波在接触线中传播时如遇到集中质量点（如中锚线夹、吊弦线夹、定位点等）将被反射，其程度可用反射因数表示，反射因数越小，则弓网耦合性能越好。反射因数r可通过下式计算：

式中：gc为承力索单位质量，kg/m；Tc为承力索工作张力，kN。目前国内尚无反射因数的相关标准，UIC 799规程中规定反射因数应小于0.4，400 km/h等级接触网可参照执行。

1.6 多普勒因数

在列车运行过程中，当遇到定位线夹等反射源时，受电弓运动状态会受到反射波的干扰，而多普勒因数则是评价运行速度和波动传播速度相互关联程度的重要参数。多普勒因数k可由下式计算：

式中：m为波动传播速度，km/h；v为运行速度，km/h。按照波动传播速度的标准进行计算，多普勒因数应大于0.18。

1.7 增强因数

受电弓经过接触网柔性较大的区段时振动较小，当经过定位点等硬点较大的区段时会周期性地激发接触线的振动，这种被激发的振动波在传播和反射时会被增强、放大[8]，增强因数R是评价该增强放大特性的指标，可通过反射因数和多普勒因数计算：

目前国内尚无增强因数的相关标准，UIC 799规程中规定增强因数不大于2.3，400 km/h等级接触网可参照执行。

2 400 km/h接触网系统参数研究

2.1 系统输入条件分析

本节从接触网悬挂类型、张力配置、跨距、结构高度、弹性吊索配置、第一吊弦点布置等方面对系统参数进行研究。结合350 km/h等级接触网的运行经验，悬挂类型按弹性链形悬挂方案考虑。

2.1.1 结构高度计算

按照现有运行经验，接触网结构高度取1.1～1.8 m，结构高度对接触力偏差结果的影响如图1所示。由图1可知，结构高度在1.8 m时接触力标准偏差最大为29.0 N，结构高度在1.6 m时接触力标准偏差最大为28.8 N，几种结构高度均满足标准要求。由结构高度不同引起的接触力标准偏差最大变化仅为0.2 N，对接触网受流性能的影响非常小。经过分析可知：结构高度较小时，吊弦长度较短，接触网弹性较差，容易形成硬点[9，10]；当结构高度过大时，由于吊弦长度增加，集中质量增大，弓网接触时引起的反射也加大，对弓网接触产生一定的影响，同时结构高度过大会导致吊弦、腕臂、支柱等材料增加。因此，综合仿真结果和国内高速铁路应用现状，建议400 km/h等级接触网结构高度取1.6 m。

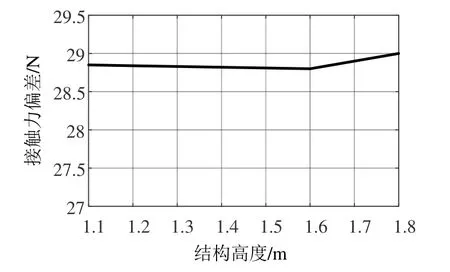
图1 结构高度对接触力偏差的影响

2.1.2 第一吊弦点布置

第一吊弦点位置主要受拉出值、张力、定位器坡度等因素控制[11]。当结构高度取1.6 m时，结合工程经验，分析第一吊弦点与支柱间距为4～7 m时的接触力标准偏差，仿真结果如图2所示。

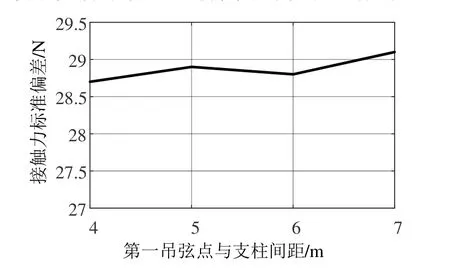
图2 第一吊弦点位置对接触力标准偏差的影响

由图2可知：第一吊弦点与支柱间距在7 m时，接触力标准偏差最大为29.1 N，在4 m时最小为28.7 N，几种第一吊弦位置均满足标准要求；第一吊弦与支柱间距由4 m增加到7 m，接触力标准偏差变化最大为0.4 N，可见第一吊弦点位置对弓网受流性能的影响较小。考虑到定位器坡度标准范围和工作张力的影响，结合目前国内的应用情况，建议第一吊弦与支柱间距标准取值5 m，同时可根据实际工程应用在4～7 m范围内调整。

2.1.3 弹性吊索配置

弹性吊索的长度和第一吊弦点的布置紧密相关，同时受腕臂安装情况的影响。考虑到400 km/h接触网第一吊弦位置以及腕臂安装基本与国内350 km/h等级接触网的常规配置相同，结合国内应用情况，一般弹性吊索张力按3.5 kN选取，长度取18 m，当第一吊弦与支柱间距为7 m时弹性吊索长度取22 m。

2.1.4 张力配置

根据波动传播速度反向计算，接触线工作张力不应小于34.5 kN，在UIC 799标准中要求400 km/h等级接触线张力应不小于35 kN。结合国内对于高速铁路的研究成果以及国内外实际应用情况，接触线张力按35、36、37、38、39 kN，承力索张力按20、21、23 kN等配置组合进行对比分析。

2.1.5 跨距

参考近年来国内外项目冲高试验段调研情况，同时结合目前国内标准规范，400 km/h接触网跨距分别按50、55、60、65、70 m进行对比分析。

2.2 接触网动态评价参数计算

在相同导线的情况下，波动传播速度仅与张力大小相关，波动传播速度大，则受流质量好；多普勒因数与运行速度和波动传播速度相关；增强因数通过反射因数和多普勒因数计算；反射因数仅与接触悬挂本身特性相关，与外部环境无关。根据系统输入参数，不同张力组合下接触网动态参数仿真计算结果如图3和图4所示。

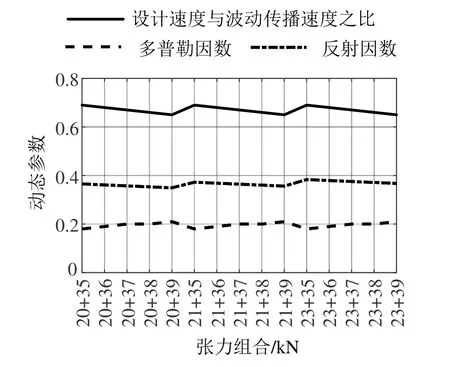
图3 动态参数随张力变化曲线

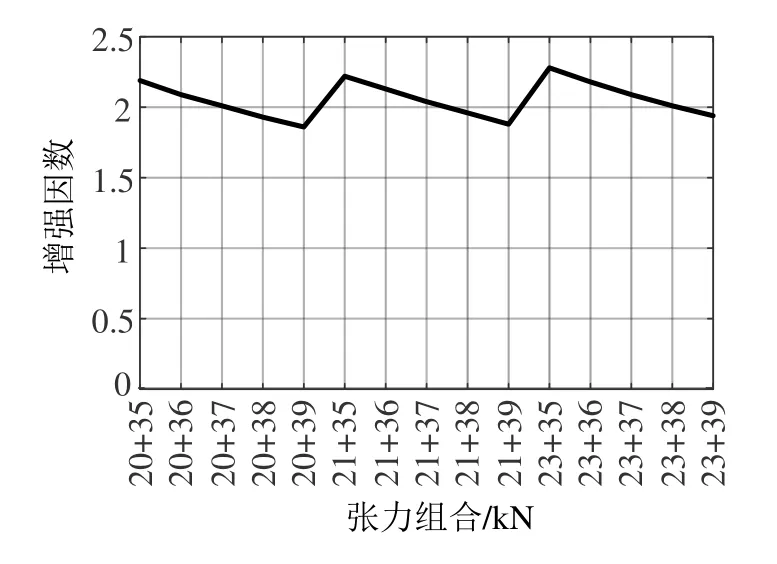
图4 增强因数随张力变化曲线

由图3可知：随着接触线张力的增加，波动传播速度逐渐增大，设计速度与波动传播速度之比则逐渐减小，几种张力组合的设计速度与波动传播速度之比均小于0.7，满足标准要求，且最小值为0.644，此时接触线张力最大；图中几种张力配置组合的多普勒因数均大于0.18，满足标准要求；图中几种张力配置组合的反射因数均小于0.4，同时随着承力索张力的增加，反射因数逐渐增大，而随着接触线张力的增加，反射因数逐渐减小，因此为减小反射系数，提升弓网受流质量，应减小承力索张力，增大接触线张力。由图4可知，各张力配置下增强因数均小于2.3，满足标准要求。

2.3 接触网系统参数对比分析

利用仿真软件针对不同张力组合和不同跨距下接触网后弓接触力标准偏差值和离线率进行分析，仿真分析结果如图5和图6所示。

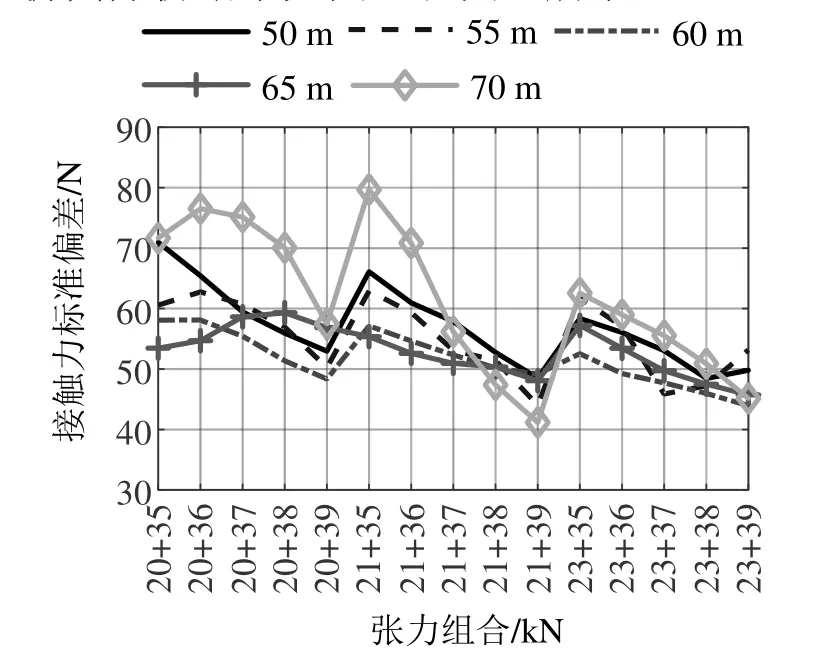
图5 跨距、张力对后弓接触力标准偏差值的影响

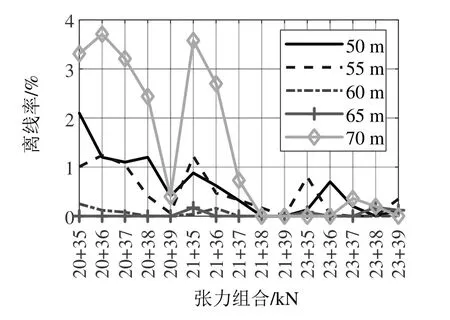
图6 跨距、张力对离线率的影响

首先对跨距进行分析，由图5和图6可知，当跨距为60 m左右时，接触力标准偏差和离线率相对较小，跨距为55、65 m时次之，这3种跨距可作为推荐跨距。在实际工况中，外界风载荷引起的接触网风偏对跨距影响非常大，因此本次研究可将60 m跨距作为推荐标准跨距，最大跨距值不超过65 m。在实际应用中，在仿真计算的基础上应考虑区域风速、线路布置等工程因素综合选取跨距。

在50～65 m跨距的范围内对接触悬挂张力进行分析。由图5和图6可知，20 kN+35 kN、20 kN +36 kN、21 kN+35 kN等张力组合的接触力标准偏差大于68 N，而20 kN+35 kN、20 kN+36 kN、20 kN +37 kN等张力组合离线率较大，不适合作为推荐张力组合。从剩余几种满足标准要求的张力组合中可以看出，随着接触线张力和承力索张力的增大，接触力偏差值均逐渐减小，但是接触线张力对接触力标准偏差的影响明显大于承力索张力。

从仿真计算角度考虑，张力越大则受流质量越好，但是在实际应用中接触线所能承受的额定张力是有限的，因此在设计过程中应充分考虑系统安全裕度，在满足接触力标准偏差和离线率的基础上尽量减小接触线张力。由图5、图6可知，当接触线张力为36 kN时，接触力标准偏差值和离线率均较小，同时满足现有接触线的许用张力，可作为推荐张力。在接触线工作张力为36 kN时，对应的承力索张力可为21 kN或23 kN。对比两种张力组合的仿真数据，从弓网接触力标准偏差和离线率两个指标分析，张力组合23 kN+36 kN均略优于张力组合21kN+36kN。

2.4 静态弹性不均匀度

对一个跨距而言，通常静态弹性不均匀度为

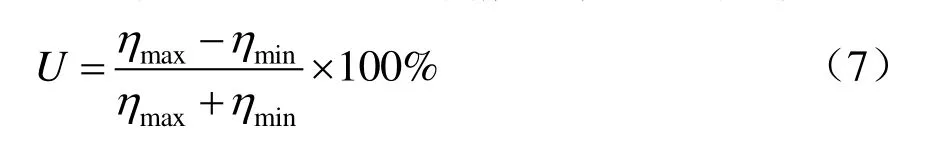
式中：ηmax、ηmin分别为指定跨距内弹性值的最大值和最小值。而跨距内弹性值η(x)计算式为

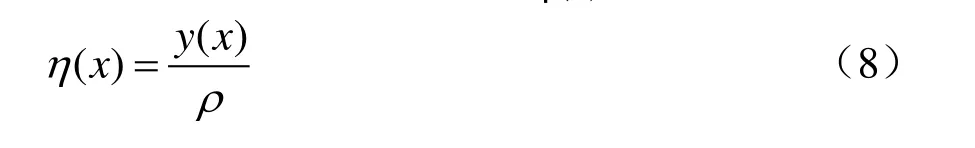
式中：ρ为抬升力，N；y(x)为由抬升力ρ在x处引起的抬升量，mm。

由于在不同抬升力的作用下，接触网系统弹性呈非线性变化，因此需要定义一个标准对静态抬升量进行计算。目前国内尚无400 km/h等级接触线抬升量的明确标准，参考京沪高铁实测报告中采用的接触线抬升量40 mm作为本次研究的标准[12]。

在动态参数分析之后，分别对两种备选的张力组合进行静态分析对比，通过仿真计算，两种张力组合的静态弹性不均匀度结果如表2所示。

表2 静态弹性不均匀度对比

由表2可知，两种张力组合的静态弹性不均匀度均小于10%，满足标准要求。同时可以发现，两者的弹性不均匀度比较接近，23 kN+36 kN张力组合配置的静态指标相对较好。

3 结语

本文建立了时速400 km高速铁路接触网系统参数系统评价标准，具体如表3所示。

表3 时速400 km接触网系统参数评价标准

通过有限元仿真计算得出时速400 km高速铁路接触网系统参数推荐值如下：

（1）时速400 km等级高速铁路接触网推荐采用全补偿弹性链形悬挂。

（2）推荐第一吊弦与支柱间距标准取值5 m，实际工程应用可考虑系统张力、拉出值、定位器坡度等综合因素，在4～7 m范围内调整。

（3）推荐弹性吊索张力取3.5 kN，长度取18 m，当第一吊弦与支柱间距为7 m时长度取22 m。

（4）综合技术经济性能，接触网结构高度推荐按1.6 m选取。

（5）接触网标准跨距推荐采用60 m，最大不宜超过65 m。

（6）推荐接触网张力组合为接触线额定张力36 kN，承力索额定张力23 kN。