平行双边供电系统数学模型研究

晏 寒，解绍锋，王 辉，马庆安

0 引言

我国电气化铁路一直采用单边供电方式[1]，为了减小三相电压不平衡对电力系统的不利影响，相邻供电臂需进行循环换相，因而在牵引变电所和分区所处存在电分相[2]。组合式同相供电技术可以在治理电能质量问题的同时取消牵引变电所处的电分相，工程应用中已取得了不错的效果[3]。鉴于我国铁路高速化、重载化的发展需求，文献[4]进一步提出的同相贯通式牵引供电系统得到了研究人员和设计人员的重视，文中提到的双边供电方案，因电力输电线与牵引网视为平行结构，而被称为平行双边供电，该方案是实施同相贯通供电的前提。

双边供电方式可以提高牵引网电压，减少电能损耗，提高牵引网供电能力[5]，还可以进一步取消 分区所处的电分相，提高牵引网的供电可靠性。但是，平行双边供电产生的均衡电流会影响电力系统的安全运行，同时会产生额外的电费计量问题[6]。既有文献在计算均衡电流时均假设牵引变电所高压母线之间的贯通输电线路直接相连。俄罗斯的牵引供电系统能满足该前提，但我国牵引供电系统的外部电源结构有所不同[7，8]。文献[9]提出了一种树形双边供电方案，可以实现无均衡电流的双边供电，是一种比较理想的方案，但其对外部电源的构造有一定要求[10，11]。

构建平行双边供电系统的数学模型，对均衡电流进行准确预估，对于平行双边供电技术的工程应用具有重要意义。对供电能力进行准确分析，也能够为电气化铁路牵引供电方案的设计提供重要依据。本文通过建立平行双边供电系统的数学模型，研究均衡电流的计算方法，以复线直供牵引网为例，分析不同并联方式的牵引网等值阻抗，并搭建仿真模型，对理论推导的准确性进行验证。

1 平行双边供电方案

图1为平行双边供电方案示意图，SS1、SS2为实施双边供电的两个牵引变电所，分别为两侧三相电力系统电压。为了取消牵引变电所出口处的电分相，牵引变压器首选单相接线变压器；同时，为了减小负序对电力系统的影响，通常采用组合式同相供电技术与之配合。图1中两个牵引变电所内分别设置单相牵引变压器TT和同相补偿装置CPD构成单相组合式同相供电，用于取消牵引变电所处的电分相，同时治理电能质量问题。将分区所两侧牵引网连通，取消分区所处电分相，形成平行双边供电。牵引网为复线直接供电方式，T1和T2分别为上、下行接触网；R1和R2分别为上、下行钢轨。

图1 平行双边供电方案系统示意图

2 平行双边供电系统数学模型

单线牵引网不存在上下行电磁耦合，其结构和分析方法较为简单。复线牵引网由于上下行存在电磁耦合，电气特性更加复杂，分析方法也与单线牵引网有所不同。

2.1 当量自阻抗

平行双边供电系统等值电路如图2所示，由于同相补偿装置CPD的潮流可调可控，在建立数学模型时可将其省去，这里仅保留单相牵引变压器。图中：ZJ11、ZJ12和ZJ21、ZJ22为牵引变电所的进线阻抗；ZTT1和ZTT2为折算到牵引网侧的牵引变压器漏抗；分别为列车处左右两侧接触网电流；分别为列车处左右两侧钢轨电流；为下行接触网电流；为下行钢轨电流；为列车取流；A为列车所在位置到左侧牵引变电所的距离；L为构成双边供电的两牵引变电所间距离。

图2所示电路上行接触网、钢轨与下行接触网、钢轨存在耦合。为便于后续分析，需先求解各导线消去互阻抗后的当量自阻抗。

图2 平行双边供电系统等值电路

设上、下行接触网的自阻抗分别为ZT1、ZT2；上、下行钢轨的自阻抗分别为ZR1、ZR2；上行接触网与上行钢轨之间、下行接触网与下行钢轨之间的互阻抗分别为ZT1R1、ZT2R2；上下行接触网之间的互阻抗为ZT1T2；上下行钢轨之间的互阻抗为ZR1R2；上行接触网与下行钢轨之间、下行接触网与上行钢轨之间的互阻抗分别为ZT1R2、ZT2R1。

由于牵引网在两个牵引变电所处上下行并联，上下行的电压降落应相等，即

将式（1）和式（2）代入式（3），并整理得

式中：Z1、Z2、Z3、Z4分别为上行接触网、上行钢轨、下行接触网、下行钢轨的当量自阻抗，Z1=ZT1-ZT1R1-ZT1T2+ZT1R2，Z2=ZR1-ZT1R1-ZR1R2+ZT2R1，Z3=ZT2-ZT2R2-ZT1T2+ZT2R1，Z4=ZR2-ZT2R2-ZR1R2+ZT1R2。

若将上下行牵引网视为对称布置，可进一步简化得

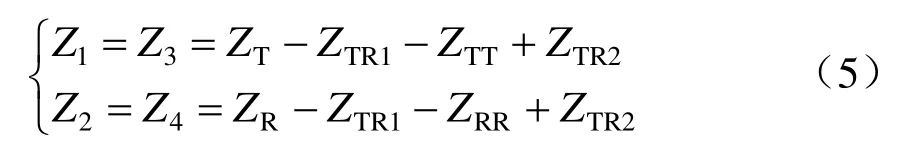
式中：ZT=ZT1=ZT2；ZR=ZR1=ZR2；ZTT=ZT1T2；ZRR=ZR1R2；ZTR1=ZT1R1=ZT2R2；ZTR2=ZT1R2=ZT2R1。

后续分析中，将默认牵引网为对称布置。

2.2 均衡电流分析

既有文献一般假设双边供电系统采用贯通输电线路供电，将牵引网的外部供电方式简化为单回路T接方式。平行双边供电方案中，均衡电流与两侧三相电源的电压差和系统阻抗有关，本文提出一种适用于该方案的均衡电流计算方法。

平行双边供电复线直供牵引网空载时的等值电路如图3所示。图中：为三相电力输电线的电流；分别为两侧三相电力系统电压；PCC1和PCC2为牵引变电所连接到高压侧的公共连接点；L1为左侧三相电源到PCC1的距离；L2为PCC1和PCC2之间的距离；L3为右侧三相电源到PCC2的距离；ZD为三相电力输电线的单位阻抗；L为构成双边供电的两个牵引变电所之间的距离；分别为两个牵引变压器原、次边电压；为均衡电流；k为牵引变压器变比。

图3 平行双边供电空载牵引网等值电路

根据图3中三相电力输电线的电压差，可得

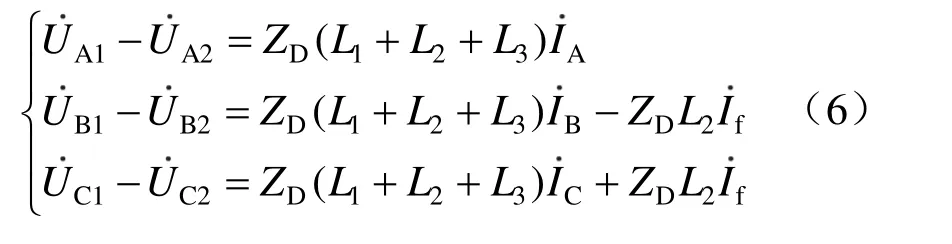
根据牵引变压器原边和次边的电压电流关系，可得

式中：ZJS=ZJ11+ZJ12+ZJ21+ZJ22。

根据式（6）、式（7），解得

2.3 牵引网阻抗分析

复线牵引网通常会进行上下行并联，为对比分析，下文以直接供电方式为例，对双边供电区间上下行不并联、末端并联和全并联3种形式的牵引网阻抗进行分析。

2.3.1 不并联直供牵引网

双边供电区间不并联直供牵引网归算到牵引侧的等值电路如图4（a）所示。图中：A为列车所在位置到左侧牵引变电所的距离；L为构成双边供电的两牵引变电所间距离；ZS1、ZS2分别为两个牵引变电所折算到牵引网侧的系统阻抗，其值为

对图4（a）所示的等值电路进一步简化，得到的简化电路如图4（b）所示。

从图4（b）中电流İ处看进去的不并联直供牵引网等值阻抗Zbi1为

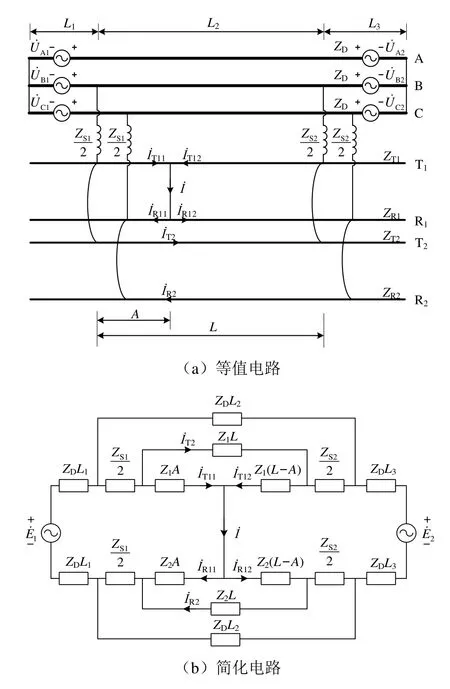
图4 双边供电区间不并联直供牵引网电路

式中：

2.3.2 末端并联直供牵引网

双边供电区间末端并联直供牵引网归算到牵引侧的等值电路如图5（a）所示，在分区所位置设置1组并联线，D为左侧牵引变电所到分区所的距离。将图5（a）进一步简化得到的简化电路如图5（b）、图5（c）所示。

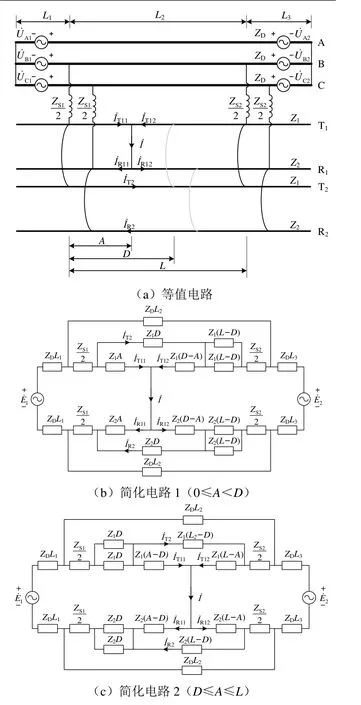
图5 双边供电区间末端并联直供牵引网电路

2.3.3 全并联直供牵引网

双边供电区间全并联直供牵引网归算到牵引侧的等值电路如图6（a）所示，在区间内每隔一定距离设置1组并联线，D为列车所在并联区段的长度，x为列车到其左侧并联线的距离。将图6（a）进一步简化，得到的简化电路如图6（b）所示。

图6 双边供电区间全并联直供牵引网电路

从图6（b）中电流İ处看进去的全并联直供牵引网等值阻抗Zbi3为

3 仿真分析

根据第2节理论分析，基于Matlab/Simulink仿真软件搭建复线直供牵引网的平行双边供电系统仿真模型，进行仿真验证。设输电线路与牵引网平行架设，L=L2= 30 km，L1=L3= 10 km，两牵引变电所进线均为10 km，牵引变压器为单相变压器，接于110 kV三相电力系统的BC相。架空输电线采用LGJ-185单导线，牵引网接触线型号CTAH-150，承力索型号JTM-150，钢轨型号P60。

电力系统合环时，要求合环点两端相序一致，电压差绝对值和相角差均不超过20%即可[12]。在仿真中设置两侧三相电源相序相同，各相电压模值相等，相角差为2°，即= 63.51∠2° kV，63.51∠-118° kV，63.51∠-238° kV，63.51∠0° kV，= 63.51∠-120° kV，= 63.51∠-240° kV，则有

图7 仿真电流波形

表1 电流有效值理论计算与仿真结果对比 A

由表1知，仿真结果与理论计算结果接近，验证了2.2节电流计算理论的正确性。此外，根据式（8），若能增大牵引变压器变比，或如文献[4]所述在牵引变压器上串联电抗器，则能够进一步减小均衡电流。

根据式（10）～式（12），设全并联时并联区间的长度D= 10 km，绘制平行双边供电系统3种并联方式的牵引网阻抗曲线如图8（a）所示。采用开短路法，在仿真模型中每隔1 km测量1次开路电压和短路电流，取得的阻抗曲线如图8（b）所示。计算结果与仿真结果对比如表2所示。

图8 牵引网阻抗曲线

由表2可知，末端并联后牵引网阻抗约减小为不并联时的82%，仿真结果与理论计算结果接近，可以验证2.3节阻抗计算理论的正确性。

表2 牵引网阻抗最大值理论计算与仿真结果对比 Ω

根据式（12）绘制全并联牵引网阻抗最大值与并联区间长度关系曲线如图9所示，可见并联区间长度越短，牵引网阻抗最大值越小。

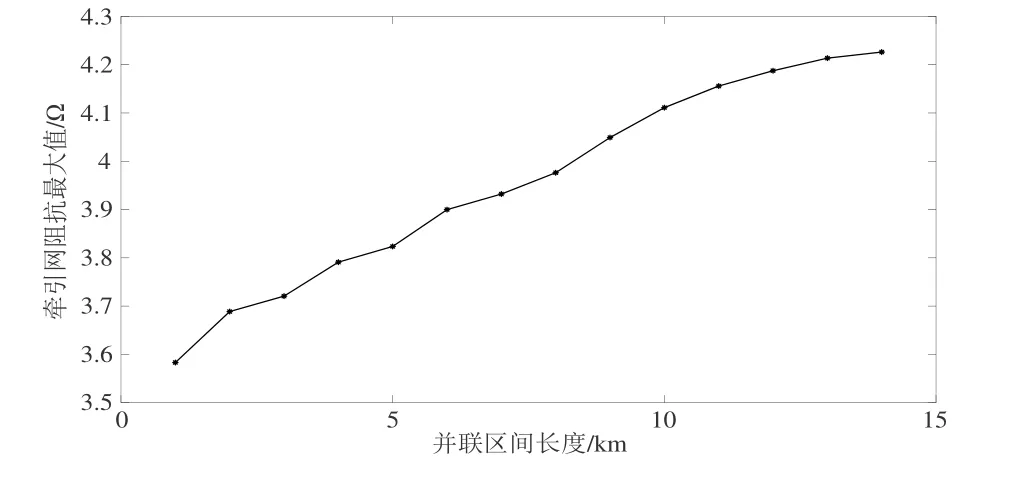
图9 牵引网阻抗最大值与并联区间长度关系曲线

4 结论

本文在考虑复线牵引网上下行各导线电磁耦合的基础上，建立了平行双边供电系统的数学模型，得到了如下结论：

（1）平行双边供电系统两侧三相电源存在电压差时，将产生均衡电流。电力系统配电网合环时，若能尽量减小合环点两侧的电压差和相角差，可有效减小均衡电流；增大牵引变压器变比，或增大牵引变压器漏抗，亦能减小均衡电流。

（2）平行双边供电系统牵引网上下行并联可以减小牵引网阻抗。并联区间长度越短，牵引网阻抗最大值越小，但考虑到牵引网的可靠性和保护配置等问题，并联区间一般不会设置得过短；工程应用中应根据列车运行图和追踪间隔等因素，合理选择并联区间长度和并联点位置，尽可能提高牵引网电压水平，降低损耗。

（3）搭建Matlab/Simulink仿真模型进行验证后表明，本文理论推导误差较小，能够为平行双边供电系统的工程应用和供电方案设计提供参考。