三相交流牵引供电系统牵引网阻抗计算

陈祯怡，解绍锋，李 洁

0 引言

在电气化铁路牵引供电系统中，接触导线的阻抗值是系统设计的重要参数，在计算牵引供电系统的供电能力时，计算系统阻抗值是不可缺少的环节之一。

系统阻抗求解的难点在于接触网导线内阻抗的计算，特别是在考虑到交流电场下导线表面电流趋肤效应时的导线内阻抗计算[1，2]。对于规则圆形截面导体而言，可使用贝塞尔函数计算导线的阻抗，但是对于非规则截面导体，由于无相应的等效半径，无法采用常规方法求解，而通常的处理方法是选取与导线等周长或等面积的圆形导体半径作为其计算半径[3，4]，该方法有一定的合理性，但是导体截面形状与圆形的偏差越大，误差越大。随着有限元方法及相应软件的兴起与广泛应用，非规则截面导体的电磁场计算变得容易实现，理论上可以计算任意形状截面的导体，并通过非均匀网格的剖分获取足够的精度[5～7]。文献[8]基于有限元ANSYS/Maxwell计算软件，给出了不同型号接触 导线交流电阻和内电感随频率变化曲线以及不同标称截面积接触导线等效半径的计算方法。文献[9]以P60型号钢轨为例，阐述了ANSYS/ Maxwell建模仿真步骤，得出不同外接圆半径下钢轨的阻抗。文献[10]利用有限元法和解析模型计算了钢轨的电阻和内电感随频率的变化关系。文献[9，11]从基本空间电磁理论角度出发，通过电气参数计算新方法的研究，提出了多导体传输线系统回路法。

针对城市轨道交通三相供电系统中供电轨的阻抗参数求解问题，本文采用ANSYS/Maxwell软件仿真求解非规则截面导体供电轨的阻抗参数，使用多导体回路法求解三相供电系统的系统阻抗，为三相供电系统供电能力的计算提供求解基础。

1 城市轨道三相交流供电系统

文中针对李群湛教授团队提出的三相交流牵引供电系统的系统阻抗进行仿真分析与计算。图1为三相交流牵引系统示意图，其中包括主变电所、三相电缆、牵引变压器、三相牵引网、车载供电系统等[12]。

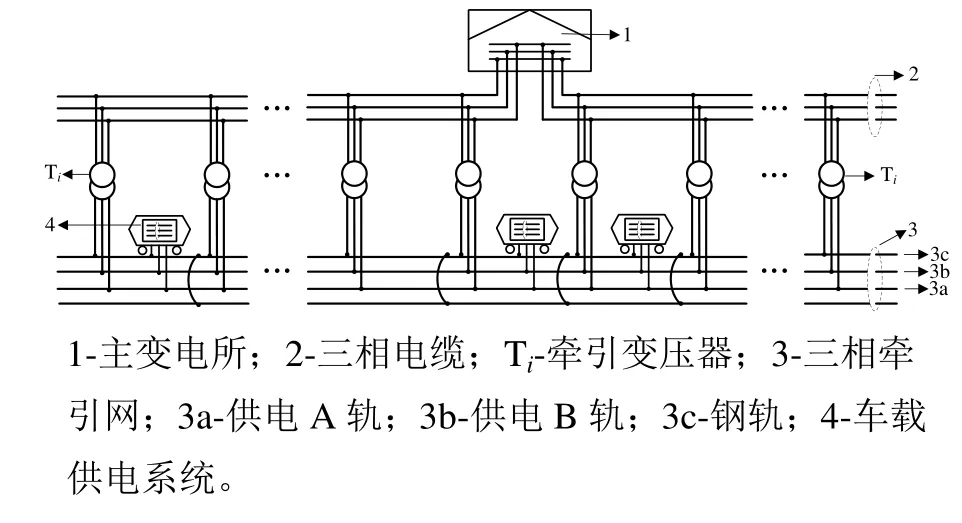
图1 三相交流牵引供电系统示意图

图2为三相牵引网示意图。三相牵引网由接触带和钢轨组成，构成“两线一地”接触结构。接触带由供电A轨、供电B轨和绝缘底座及绝缘护盖组成，铺装于两钢轨中间，供电A轨、供电B轨的安装高度高于钢轨的顶端[13]。

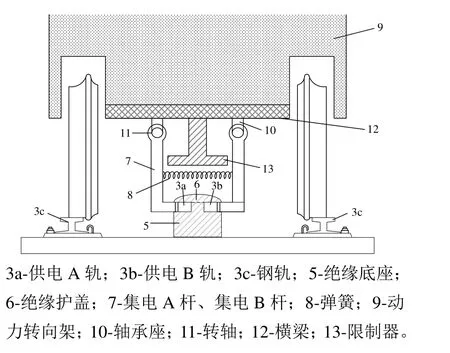
图2 接触带与受电犁结构示意图

2 钢轨内阻抗有限元计算

由于供电轨为不规则导体，阻抗难以计算，故使用ANSYS有限元仿真软件进行仿真计算得到供电轨的阻抗。为证明求解供电轨内阻抗仿真方法的正确性，先将该仿真方法用于P60钢轨内阻抗计算，将仿真结果与P60钢轨内阻抗的现有结果进行对比[8～10]。

在ANSYS/Maxwell软件中，计算导体内阻抗的参数设置步骤：建立图形→设置求解器→添加编辑材料属性→设置边界条件→添加激励→设置划分网格→求解设置→数据导出。

参照国家铁道行业标准TB/T 2809—2017，在Auto CAD中绘制P60型号钢轨截面图。将P60钢轨截面的CAD图形导入ANSYS/Maxwell软件，找到坐标原点后，在钢轨外围任意设置一个可以包裹住钢轨的外边界圆，用以设置计算时的边界条件，外边界圆半径从120 mm开始设置，在钢轨断面上添加100 A的交流电流，仿真计算结果见表1。

取表1中10组数据的平均值，得到钢轨内电阻为0.137 Ω/km，内电抗为0.135 Ω/km。根据文献[14]，100 A电流情况下单条P60型号钢轨内电阻为0.135 Ω/km、内电抗为0.135 Ω/km，仿真结果与之对比，误差分别为1.48%、0%，可知该仿真结果与实际现有参数相差不大。钢轨材料与供电轨中钢部分使用的材料相同，因此该仿真方法可适用于供电轨内阻抗的参数求解。

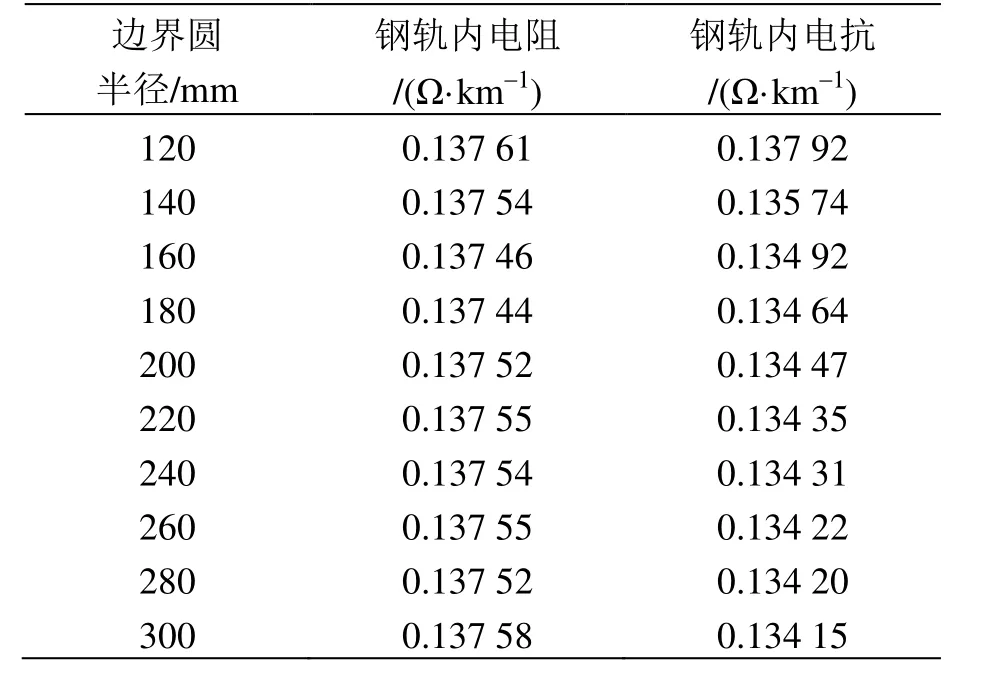
表1 不同边界圆半径对应的钢轨内阻抗计算结果

3 供电轨有限元软件计算

3.1 供电轨内阻抗仿真

由于供电轨与集电杆相接触部分的钢材质一面为弧面，为了简化装置，将弧面视为平面。设置供电轨为长63 mm、宽60 mm的矩形，顶端附有3 mm长的钢材料，下端为导电材料铝，在Auto CAD中绘制供电轨截面图形如图3所示。

图3 供电轨截面的CAD图形

将供电轨截面的CAD图形导入ANSYS/ Maxwell软件中，找到坐标原点后，在供电轨外围任意设置一个可以包裹住供电轨的外边界圆，用以设置计算时的边界条件，外边界圆半径从50 mm开始设置，在供电轨断面上添加100 A的交流电流。供电轨内阻抗仿真结果见表2，取该10组数据的平均值，得到供电轨内电阻为0.015 5 Ω/km，内电抗为0.025 6 Ω/km。

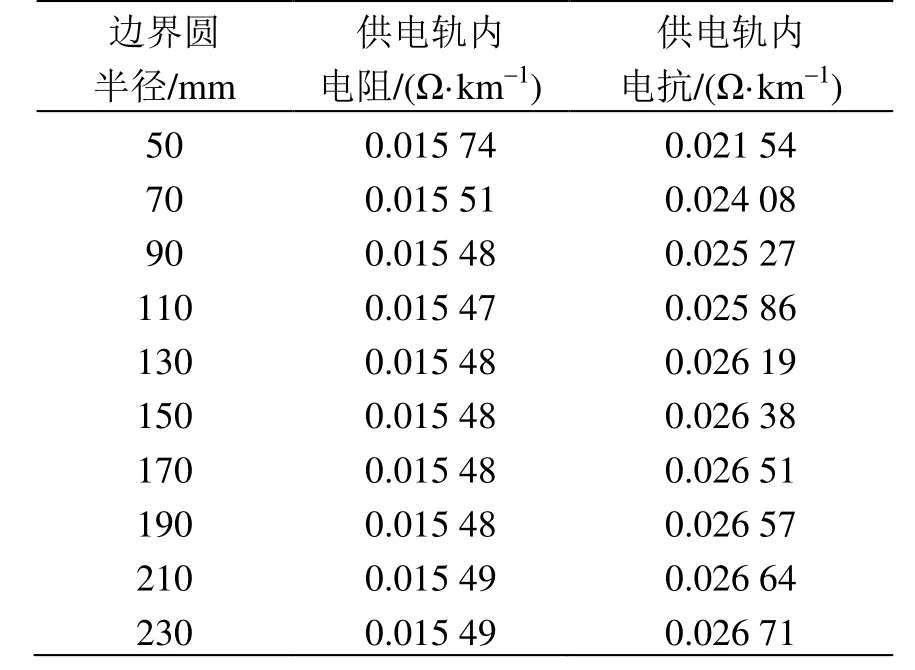
表2 不同边界圆半径对应的供电轨内阻抗计算结果

3.2 供电轨等效半径计算

根据上文仿真还可得到供电轨的内电感Lin，其结果是由总电感L减去外电感Lout得到。在实际网络计算中，外电感Lout与供电轨等效半径Rε有关，当需要计算供电轨与其他导线的互阻抗时，等效半径Rε是计算的一个重要参数，在有限元仿真中，可以根据外电感Lout确定等效半径Rε。

由于内电感Lin与频率及导体电流分布有关，频率趋于无穷大时，电流集中在导体表面，这时内电感接近于零，因此当频率趋于无穷大时，外电感Lout与L相等[10]。利用有限元仿真方法计算供电轨频变参数，可以发现电感L最后趋近于一个稳定值，此时计算结果趋近于外电感Lout，取极限频率f= 107Hz，获得外电感Lout[15，16]。通过导线与大地的回路电感L的计算式反算等效半径Rε，即

式中：D1p为包围导线的圆半径，仿真中等于外界圆半径；μ0为真空磁导率，μ0= 4π×10-4H/km。

在f= 107Hz情况下，设置不同的外界圆半径，得到5组不同外界圆半径情况下的外电感及相应的等效半径计算结果，如表3所示。由结果可知，不同外界圆半径的情况下，供电轨等效半径基本不变，相差较小，结果取其平均值，即Rɛ= 36.342 mm。

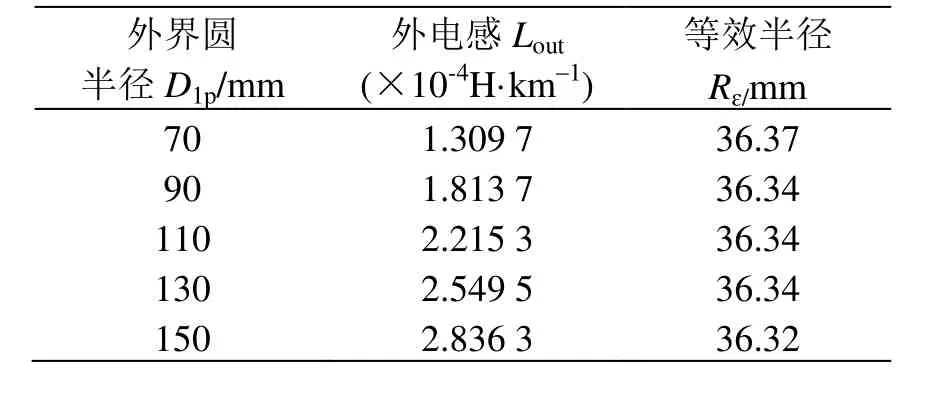
表3 不同外界圆半径情况下的外电感及等效半径

4 基于多导体回路系统的牵引网阻抗计算

牵引网阻抗的求解采用多导体回路法进行计算[9，11]。三相牵引网结构示意如图4所示。

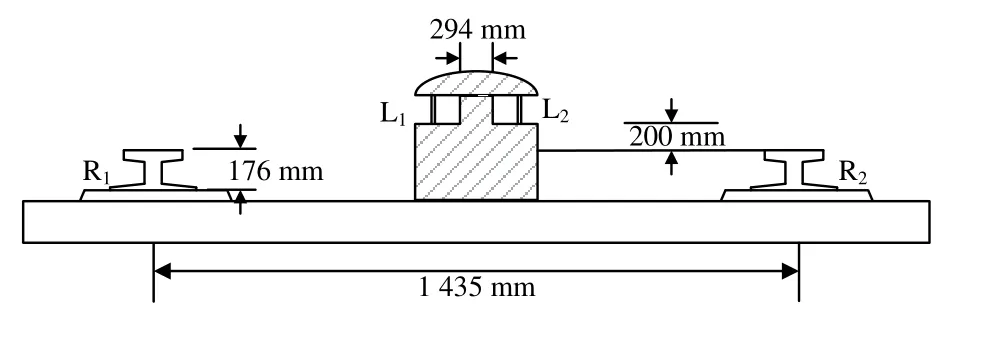
图4 三相牵引网结构示意图

假设供电轨L1、L2为传输导体，钢轨R1、R2和大地E作为回流导体，传输导体与回流导体两两分别构成6条回路，如表4所示[11]，回路示意图见图5。图中，S1为供电轨L1与钢轨R1的距离，S2为供电轨L1与钢轨R2的距离，S4为供电轨L2与钢轨R1的距离，S5为供电轨L2与钢轨R2的距离，d1为两根供电轨之间的距离，d2为两根钢轨之间的距离。

表4 各回路编号

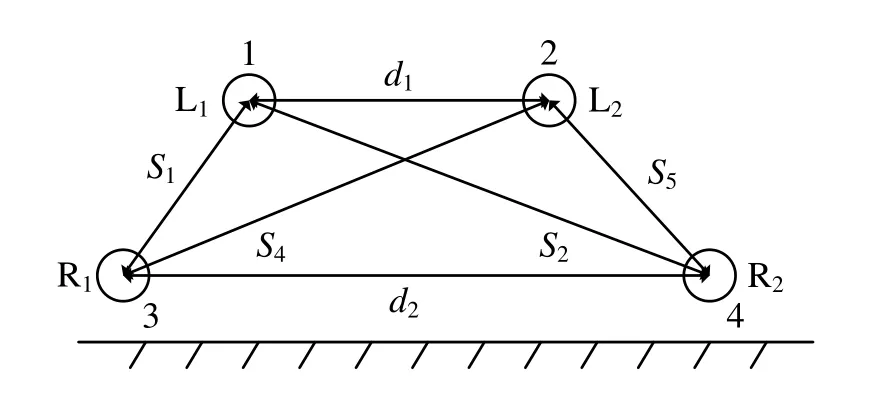
图5 回路系统示意图

基于表4，根据各回路电压降与各回路磁链关系，当电源为正弦激励时，可得各回路电压降、回路阻抗和各回路电流间关系如下：

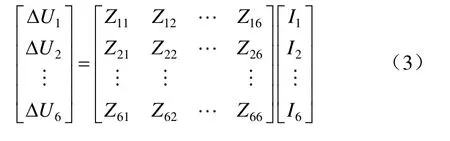
式中：Zij（i= 1, 2, … ,6；j= 1, 2, … , 6）为6条回路对应的自阻抗和两两间互阻抗；ΔUj为第j条回路的电压降；Ij为通过第j条回路的电流。

由于牵引网导线长度较长且平行，各回路可视为并联，此时有ΔU1= ΔU2= …= ΔU6。对任意回路i和回路j构成的两回路而言（i≠j），它们的磁链相等，由磁链守恒可得

式中：lij为回路对应的自电感和两两间互电感。

假设I为所有传输导线的总电流，k1、k2、…、k6为6条回路的电流分配系数，则有

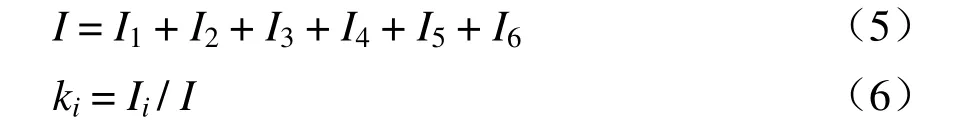
为了计算各回路电流之间的关系，先得到以下自电感与互电感：

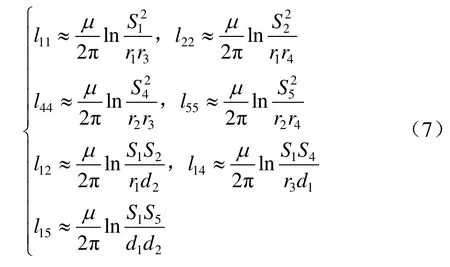
对于大地回流回路（即回路3、6），有

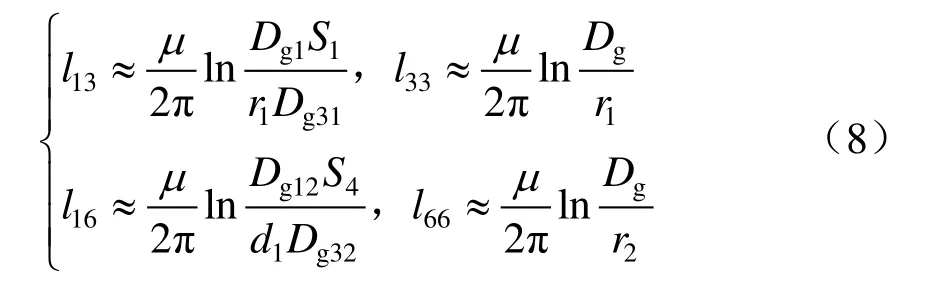
式中：ri为各导体的等效半径；μ为回路空间磁感应系数；Dg为导线对大地的等值深度；Dg1为导体1对大地的等值深度；Dg31为导体3与导体1镜像间的距离；Dg12为导体1与导体2镜像间的距离；Dg32为导体3与导体2镜像间的距离，导体的镜像由对大地的等值深度确定。

将式（7）、式（8）代入式（4），并与式（5）、式（6）联立，可得k1= 0.213 4，k2= 0.178 6，k3= 0.113 7，k4= 0.147 0，k5= 0.213 4，k6= 0.133 8。

将系数k1、k2、…、k6分别代入式（9），可得6条回路单位长度压损。

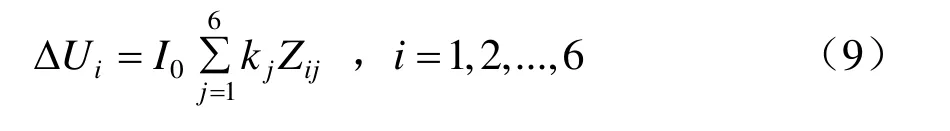
式中：ΔUi为第i条回路单位长度压降；kj为第j条回路电流分配比例；I0为牵引网总电流。

由于牵引网各回路间可并联等效，牵引网单位长度阻抗为牵引网单位长度电压与牵引网总电流比值，可得各回路等效单位长度阻抗Zi为

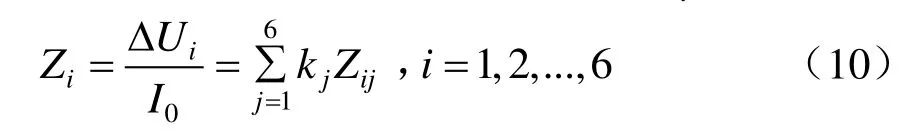
由于各回路并联，6条回路单位长度压降相等，故有Z1=Z2=…=Z6，故式（10）计算结果即为牵引网等效单位长度阻抗。

式（11）～式（14）为回路1相关的自阻抗及与其他导体回路间互阻抗计算式。

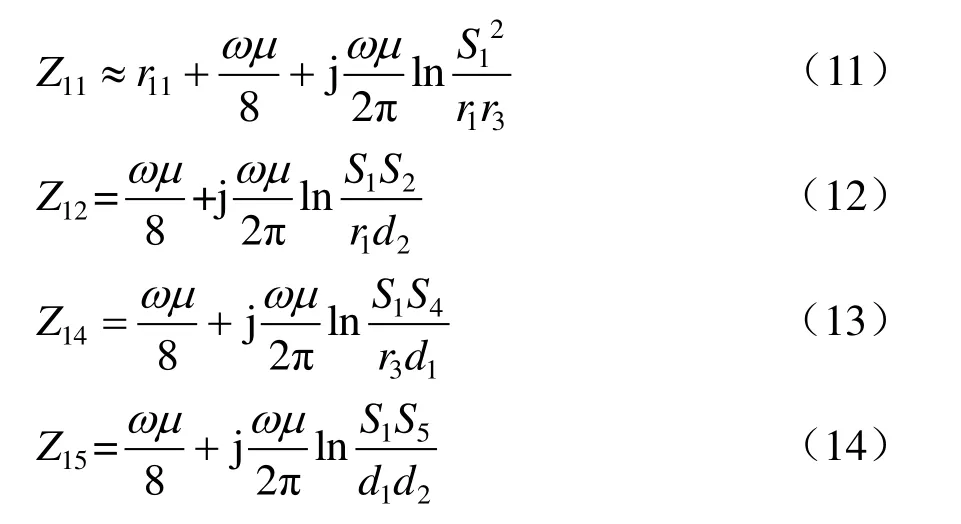
式中：ω为工频角频率，其值为2πf，f=50 Hz；Z11为回路1自阻抗；Z1j为回路1与回路j（j= 2，4，5）相交联的互阻抗；r11为回路1自电阻。

对于大地回流回路与架空回流回路间的互感抗（回路1与回路3、回路6间互感抗），计算式分别为

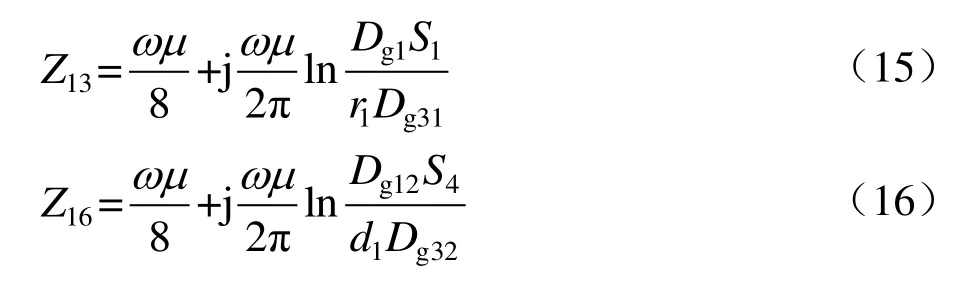
将i= 1代入式（10）中，得到等效单位长度阻抗为(0.081 1 + j0.49) Ω/km。

由于在三相交流系统中，两根供电轨和钢轨互为回流，传输导体和回流导体有6种情况，6种情况下的牵引网等效阻抗计算结果如下：

（1）两根供电轨作为传输导体，钢轨作为回流导体，等效阻抗计算结果为(0.081 1 + j0.49) Ω/km；

（2）供电轨1、钢轨作为传输导体，供电轨2作为回流导体，等效阻抗计算结果为(0.054 1 + j0.154 8) Ω/km；

（3）供电轨2、钢轨作为传输导体，供电轨1作为回流导体，等效阻抗计算结果为（0.054 1 + j0.154 8) Ω/km；

（4）供电轨1作为传输导体，供电轨2、钢轨作为回流导体，等效阻抗计算结果为(0.056 6 + j0.225 3) Ω/km；

（5）供电轨2作为传输导体，供电轨1、钢轨作为回流导体，等效阻抗计算结果为(0.056 6 + j0.225 3) Ω/km；

（6）钢轨作为传输导体，两根供电轨作为回流导体，等效阻抗计算结果为(0.078 8 + j0.211 8) Ω/km。

由于三相系统的对称性，三相牵引网等效阻抗近似为6种情况下等效阻抗的平均值，结果为 (0.063 55 + j0.244 9) Ω/km，即三相交流牵引网的等效阻抗为(0.063 55 + j0.244 9) Ω/km。

5 结论

针对采用新型受电犁供电且供电轨为不规则导体的三相交流牵引供电系统的系统阻抗求解问题，文中采用ANSYS/Maxwell有限元软件对供电轨及牵引网阻抗进行分析计算，得出以下结论：

（1）P60钢轨仿真结果中内电阻和内电抗分别为0.137、0.135 Ω/km，与现有参数的误差分别为1.48%、0%。供电轨仿真结果中内电阻和内电抗分别为0.015 5、0.025 6 Ω/km，等效半径约为36.34 mm，该等效半径参数在牵引网阻抗计算中尤为重要。

（2）根据仿真得到的供电轨阻抗及等效半径对牵引网阻抗进行计算，采用多导体回路法得到三相交流牵引供电系统的牵引网阻抗为(0.063 55 + j0.244 9) Ω/km，对三相交流牵引供电系统建模及供电能力计算具有重要参考意义。