基于变步长极值搜索的列车黏着控制方法研究

柳海科，袁忠于

（兰州交通大学 机电工程学院，兰州 730070）

随着我国高铁行业的迅速崛起，高速列车运行的节能性和轮轨黏着的有效性备受人们的关注［1-2］。在天气恶劣的情况下，由于轮轨表面受雨、雪等外界因素影响，黏着系数则会随之下降，这样可能会导致车体发生空转/滑行，最终造成轮轨擦伤、磨损，甚至脱轨等严重现象。

列车的黏着工作点处于最优蠕滑速度处（即最大黏着系数附近），是实现最优黏着控制的充分且必要条件，而此工作点处于黏滑特性的稳定区和非稳定区的交界处，同时也并非固定不变［3］。

目前有很多研究者提出多种控制方法：比较传统的组合校正等策略［4-7］多数是以设置固定的速度差和加速度的阈值作为空转的判断依据，并且通过不断地削减电机转矩来消除空转，当路面情况良好时，又逐渐增加电机转矩使列车恢复到原来较为平衡的行驶状态。而在现实中，随路况的变化，最大黏着系数和与之相应的蠕滑速度值都会随之变化。若以固定值来作判断依据，显然略显牵强，而且这种方法的黏着利用率不会很高；文献［8-9］采用的最优黏着控制策略则多数是用传统的固定步长去搜寻不同路况下黏滑特性曲线的峰值，在此过程中，固定步长的确定是一个难题，并且对控制系统的搜索精度和速度的影响也很大；在搜索峰值的过程中，获取黏滑特性曲线斜率也可采用相位移的方法，但是这种方法是建立在线性化列车的牵引动力模型之上，其频率工作点有着很差的观察范围，且至今在实际使用中也不是很成熟［10］；文献［11-12］则是将蠕滑速度看作是不断变化的固定量，其对时间微分值始终不为0，黏着峰值点的搜索只考虑了黏着系数对时间的导数，而对蠕滑速度的状态却无法证实；文献［13］则采用的是滑模极值搜索的算法，虽然可搜索极值，但会产生剧烈的抖振现象，且在达到滑模面时，此算法所用时间是有限的。

通过以上分析，文中引入了FFRLS来实时估算黏滑曲线的斜率，与此同时采用全维观测来获取负载转矩的近似值，其目的是获取更为精确的黏着系数。同时提出了一种基于Sigmoid函数的步长可变的极值搜索法，以此来结合PID控制器应用广泛且结构简单等特点，最终完成最优黏着控制，既解决了步长固定等难题，提高了控制精度，还可适应不同路况。

1 列车轮轨黏着—蠕滑原理

列车在行驶中的动力需要凭借车轮与轨道之间的相互作用来提供，这种现象的产生实际是轮轨之间产生的弹性作用所造成的，是必要的［14］。在电机的牵引作用下，车轮将受到驱动转矩的作用，会形成轮周黏着牵引力Fs。又由于存在轴载作用，这样的轮轨之间接触面可以保持相对静止的状态称为“黏着”［7］。

而蠕滑现象是滚动体在运行过程中所产生的正常微小的滑动现象，正因如此，车体前进的速度vt通常会低于车轮滚动的圆周速度vd，则蠕滑速度vs为式（1）：

定义黏着切向力和垂向荷重之间的比值为黏着系数，用μ表示，为式（2）：

式中：W为轴重；FS为轮周黏着牵引力。

经大量的试验结果分析，轮轨黏着系数μ与蠕滑速度vs有如下关系［7，14-15］为式（3）：

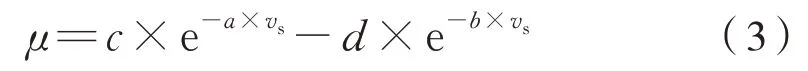
式（3）的曲线如图1所示。

图1 轮轨黏着—蠕滑特性曲线

图1 中，A点即为黏着理想峰值点μmax，是列车最佳的工作点，则最优蠕滑速度值vsref在此时产生。

显然，结合图1与式（2）可知：黏着系数和牵引力几乎是正比，因此要想使得列车黏着牵引力能够在不同轮轨条件下发挥出最优的效果，黏着系数也必须时刻达到峰值。

2 列车单轴动力学模型的建立

由于文中的最终目的是黏着控制，故本节将借助简化后的单轴动力系统来有效地反映列车在运行过程的牵引特性［14］。

在列车的实际牵引过程中，轮对传动机构受力分析如图2所示。

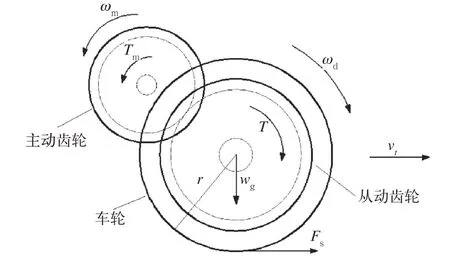
图2 轮对传动机构受力分析

由牛顿定律可知，列车运动方程为式（4）、式（5）：

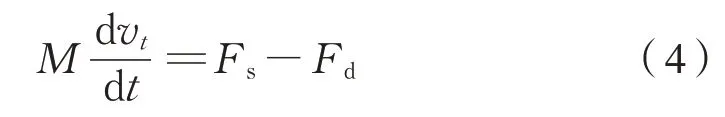
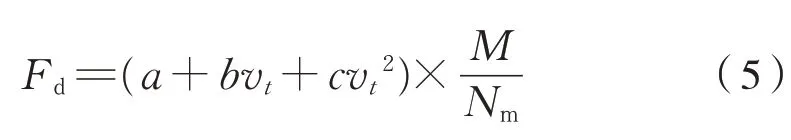
式中：M为列车质量；Nm为动轴数。

忽略阻尼，则电机输出轴转动方程为式（6）：

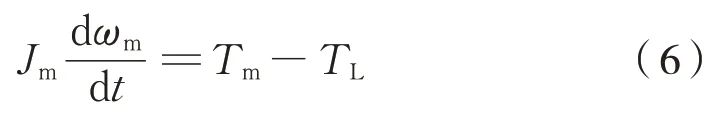
同时对车轮进行受力分析，其转动方程式（7）：

设齿轮箱传动比为i，传递效率为η。根据能量守恒得式（8）：

电机轴总惯量为式（9）：

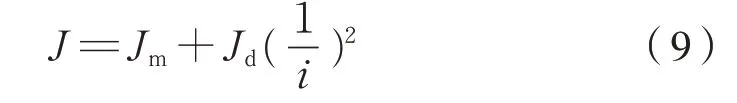
由以上各式可得等效牵引电机转动方程为式（10）：

从电机侧看，牵引电机的负载转矩可由黏着力最终折算而成，列车简化牵引模型如图3所示。

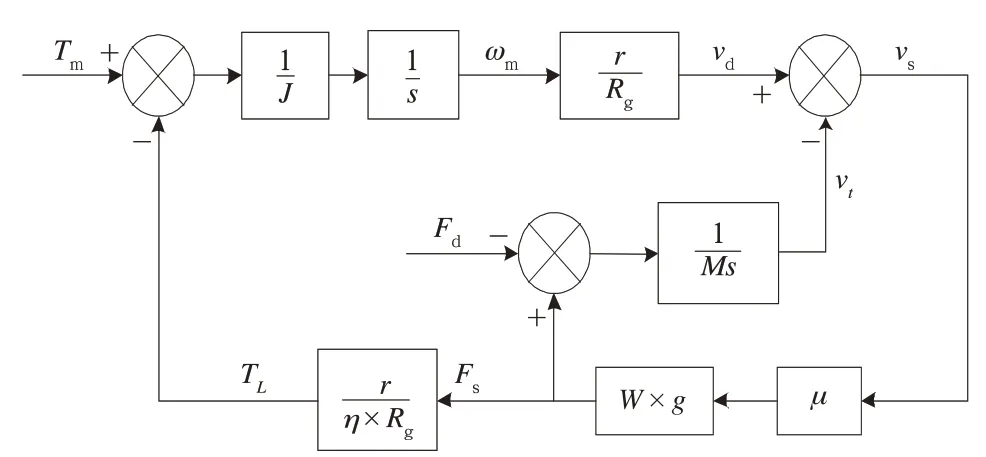
图3 列车简化牵引模型框图

3 黏着系数的估算

在系统的控制过程中，只有获取了比较准确的黏着系数，才能够达到最佳的控制效果。而黏着系数是不可以直接测量到的，故只能间接构造TL的观测器得到，它有着能够避免噪声干扰的优点，同时也可以防止由测量误差给系统性能带来的影响，通过对其他干扰和误差的有效避免，系统的稳定性将得到明显的改善。

3.1 全维状态观测器的设计

若列车行驶的潮湿区域极短，会因为在此之前已经产生了一巨大的惯性而迅速驶过，这时已经来不及快速检测和响应［12，14］。通过以上分析，文中只考虑潮湿区域较长的区域2，如图4所示。

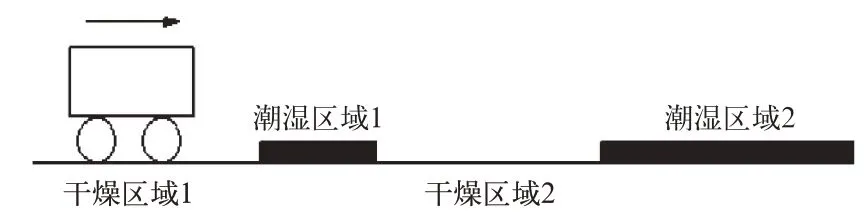
图4 列车行驶路况

由于在行驶中产生着巨大惯性，当车体驶过如图4所示的潮湿区域1时，TL基本不会发生较大的突变情况。即便在极端的状况下，电机轴又与很重的轮对经变速箱等传动装置连接，负载转矩的扰动随时间变化的量值也远大于控制系统响应的时间常数［5，9］。因此在确立全维观测系统的同时，可以考虑将机组的负载转矩近似地视其为恒定量，则有式（11）：

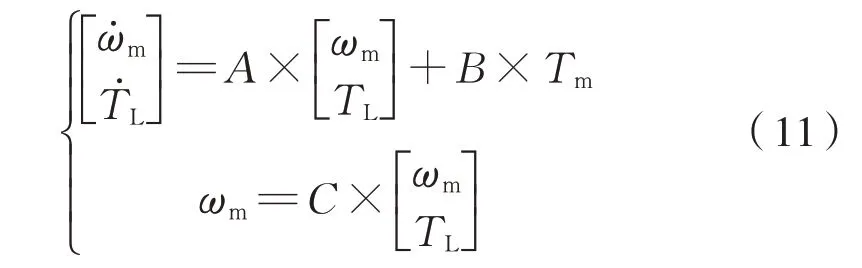
根据状态观测器有式（12）：

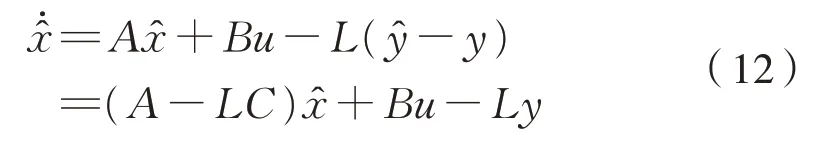
构造TL的状态观测器动态方程式（13）：

依据Lyapunov的稳定性可知，若受控对象能观，则选择观测系统的反馈增益阵须必须使(ALC)的特征值都具有负实部，这样才会使其渐进稳定［16］。设反馈增益矩阵

若设p1、p2为该状态观测器的极点，则有式（14）：

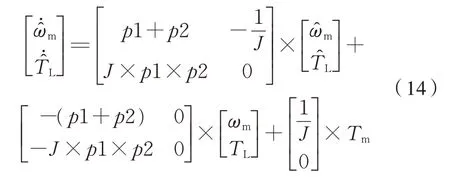
则有式（15）：

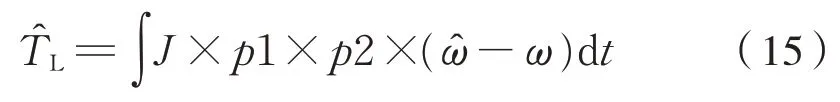
则黏着系数为式（16）：

为此，在Simulink中搭建渐进稳定的全维观测模型来实时观测列车动态，如图5所示。

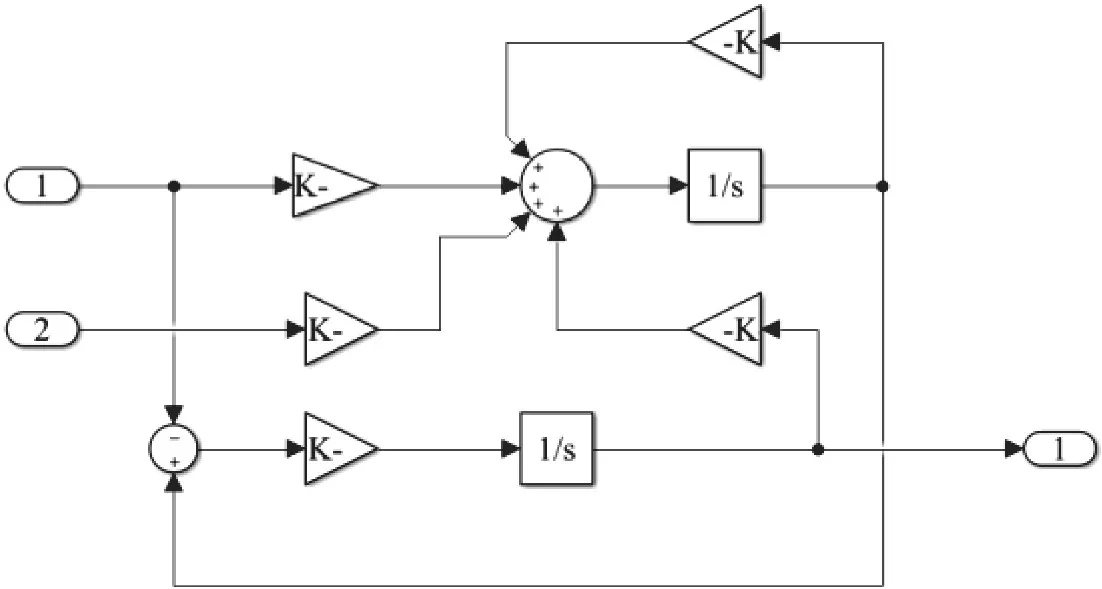
图5 全维状态观测器Simulink模块

3.2 极点配置对系统观测性能的影响

极点的配置尤为重要，其可将直接对控制系统的稳定性以及观测系统的收敛速率带来很大的影响，所以将通过误差(̂-x)的引入来分析此观测器的动态响应，最终确定配置极点。

若 有̇-̇=(A-LC)×(x-̂)，即̇=(ALC)×e，则有式（17）

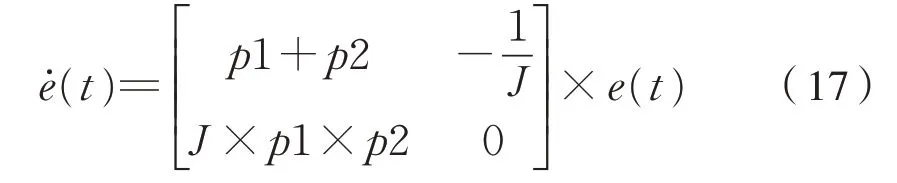
解得e(t)=Φ(t)×e(0)。

其中，Φ(t)=Laplace-1=[(sI-A+LC)-1]。

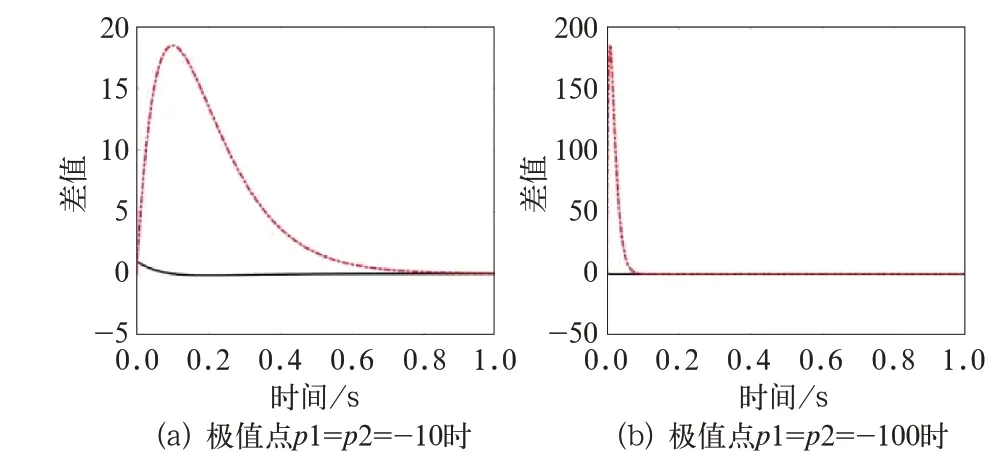
图6 估计误差衰减曲线

由图6（a）中可知，误差大概在0.8 s附近消失；图6（b）中大概在0.1 s附近消失。为了加快此观测器的动态响应效果，文中在控制系统的仿真中，观测器极点则取p1=p2=-100。

p1=p2=-100时，全维状态观测器观测到的列车负载转矩值与实际值，如图7所示。负载转矩实际值与观测值误差如图8所示。

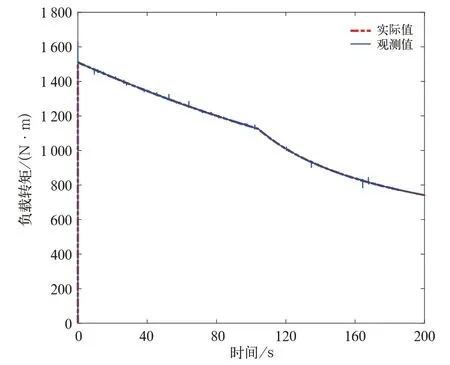
图7 负载转矩观测值与实际值

由图8得，设计的此全维状态观测系统可以较好地观测出列车的负载转矩，误差很小，在使用要求范围之内。

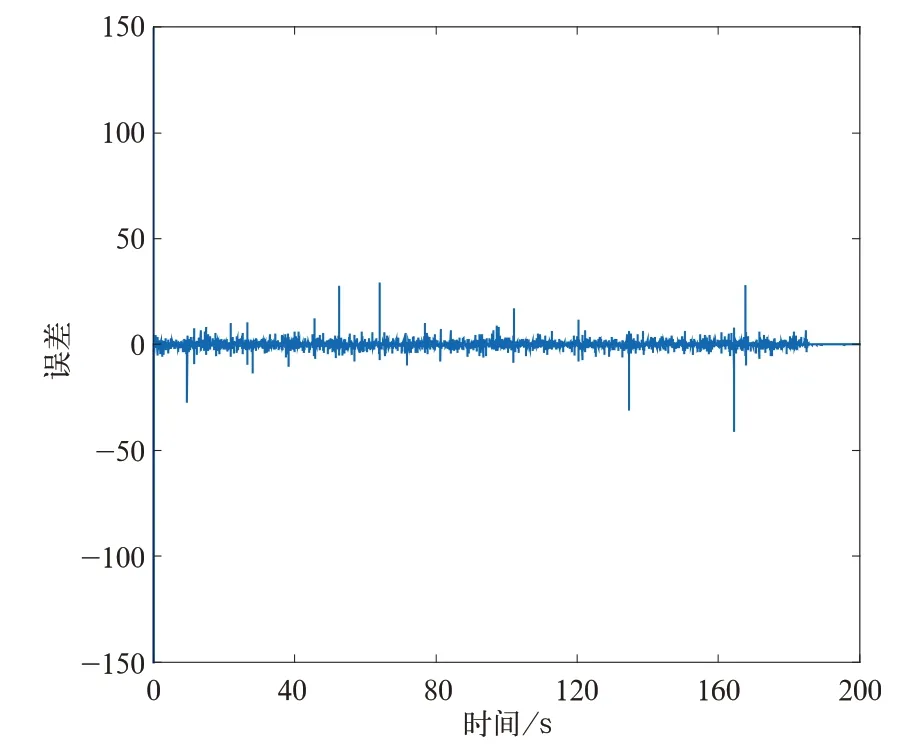
图8 负载转矩实际值与观测值误差

4 基于变步长梯度搜索的黏着控制策略

最优黏着控制的实质便是在列车运行时，可自动且迅速搜寻到当时所在路面情况的黏着峰值点，控制系统进行实时监测并快速响应，可使得列车轮轨始终在峰值点的附近处工作。

4.1 黏着控制实现原理

负载转矩最优黏着控制原理如图9所示。

图9 负载转矩最优黏着控制原理

通过上节观测出的负载转矩，由式（16）可估算出黏着系数的近似值̂；与此同时便可得到与，且利用FFRLS可估算出特性曲线斜率；根据文中的控制原理，然后加入变步长梯度法搜索出最优值(t)；再将(t)作为控制系统的目标值，利用PID模实时调节实际蠕滑速度值以不断逼近最优值，最终可得到转矩的补偿量，在控制的进行中，会实时对比机组所提供与列车运行所需的转矩，取2者最小，即为最终指令，这样可以很好地避免车轮空转，同时也可以随时使牵引转矩得到充分的利用。

贵州省黔东南苗族侗族自治州水土流失、石漠化及潜在石漠化面积分别为 8 412km2、1 314km2 和 2 166km2，分别占全州面积的 27.73%、4.33%和7.14%。水土流失及石漠化已成为全州经济社会可持续发展和全面实现小康社会目标的重要制约。

PID控制器具体形式为式（18）：

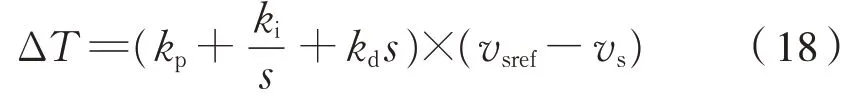
4.2 黏着曲线斜率的估计方法

根据对最小参数辨识原理［17］的分析，将原有的带遗忘因子最小二乘算法进行了改进，则在此控制系统模型中，蠕滑斜率估算的递推公式为式（19）［18］：

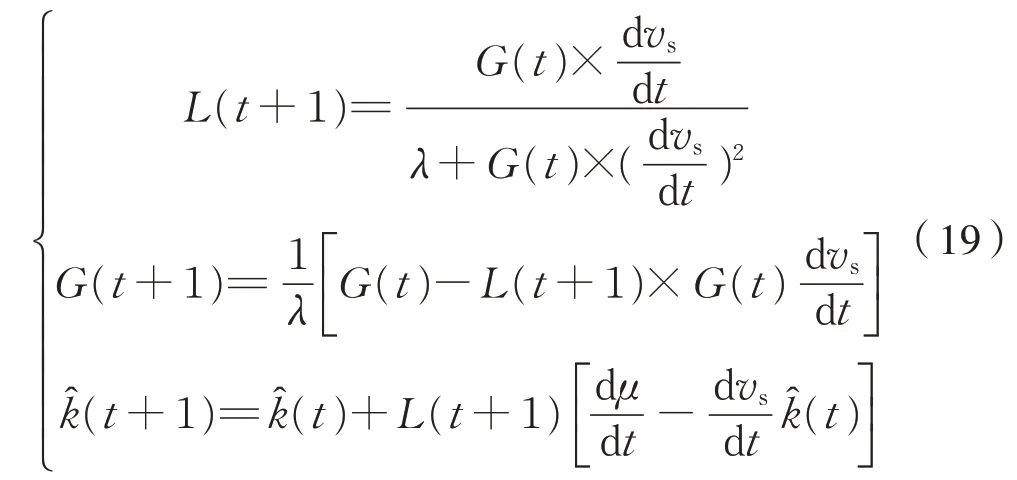
式中：λ∈(0，1)为遗忘因子；L、G为中间的变量；为黏着曲线斜率的估算值；̂(0)=0，G(0)=106I。

4.3 基于变步长梯度法的极值搜索

梯度下降算法已在各种领域中应用，是一种优化算法，其每次迭代时会由负梯度得知新的搜寻方向为负梯度方向，这种搜索方法搜索速度快，迭代效果好，可使得目标函数始终会靠近最优值。

则变步长的最优蠕滑速度为式（20）：

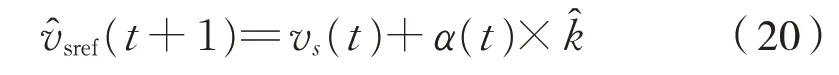
基于固定步长最优参考蠕滑速度为式（21）［8-9］：

分析知，变步长可以随着蠕滑斜率的改变进行随时调整，以弥补固定步长速度慢和精度不足等缺点。

Sigmoid函数变换前后对比如图10所示，通过分析Sigmoid函数（图10（a））的特点［19］，提出一种改进后的算法（图10（b）），对比分析2种算法，改进后的优点在于当斜率k̂趋于零时，此算法的搜索步长随着斜率的减小可相应地增大，以确保控制系统的搜索速度。

图10 Sigmoid函数变换

Sigmoid函数变形后为式（22）：

将斜率̂代入上式，设置参数得到步长因子为式（23）：

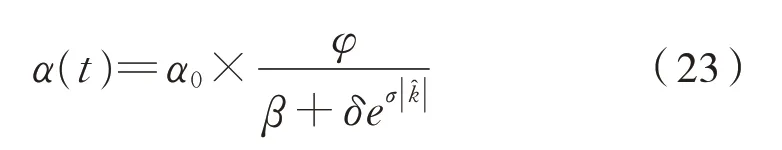
式中：α0为初始学习步长。

在控制过程中，实际工作点将会越来越靠近最大值，而此时̂将会变得越小，但与此同时α(t)会相应地增大，它的作用是避免由于̂的变小而影响(t+1)的搜索速度，将会使得(t+1)的搜索速度加快，这样确保了搜索系统在峰值点附近有足够的搜索速率。

5 仿真验证与结果分析

5.1 仿真参数设定

文中基于Simulink平台，并采用了结构原理较为简便且应用较为广泛的PID控制器来验证变步长极值搜索的优势和效果。

根据式（3），设定3种路况参数，见表1［14］。由表1可得3种路况，如图11所示。文中以CRH2A型列车为例，其仿真参数见表2。

表2 CRH2A主要参数

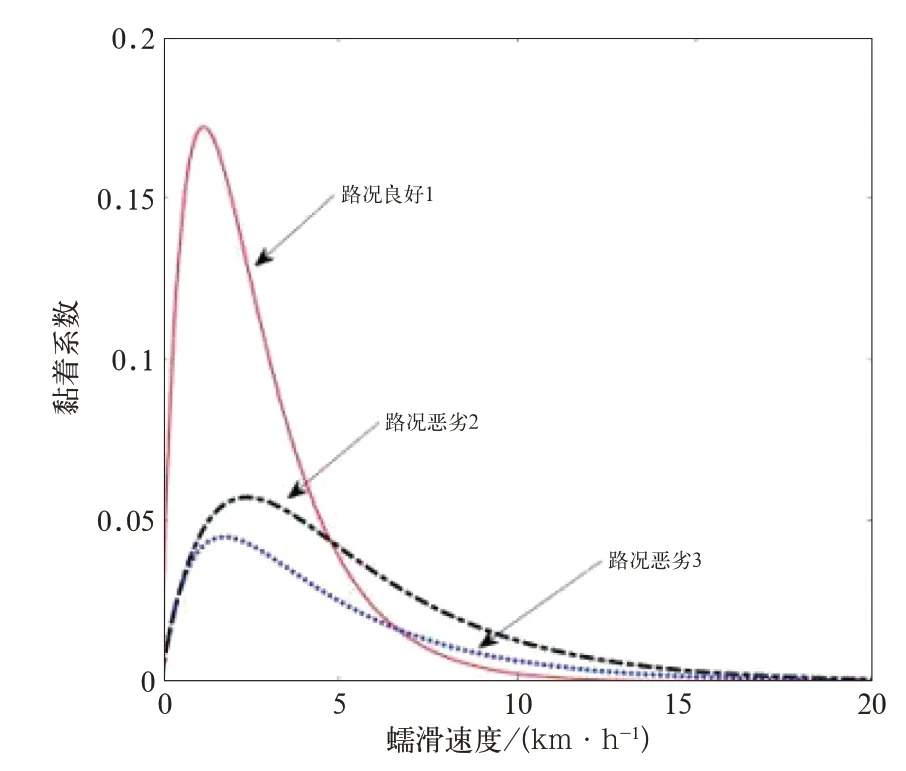
图11 不同路况的黏滑特性曲线

表1 仿真路况参数

5.2 仿真结果分析

在Simulink中，列 车 在0～40 s、80～120 s和160～200 s中为路况1；在40～80 s中为路况2；在120～160 s中为路况3；

在变步长极值搜索中，α0=10-3、β=1、δ=1、φ=1/20和σ=10；目的是验证搜索算法在不同轨面以及从干轨到湿轨发生空转时的及时响应效果，步长极值搜索方法、滑模极值搜索方法如图12、图13所示。

对比图12、图13得：变步长极值搜索能够快速响应，在处于不同的路面情况下，均可及时搜索出最优值，且搜索精度较固定步长高很多，超调量也很小；而滑模极值算法在整个搜索过程中会不断出现抖振现象，而且波动值较大，搜索速度也非常慢。

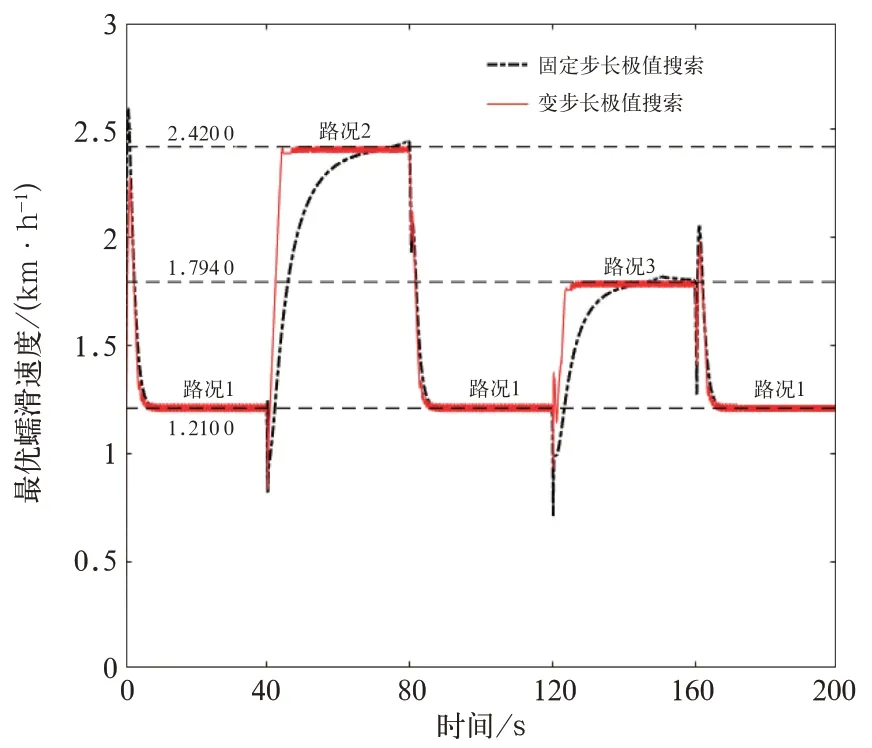
图12 步长极值搜索方法

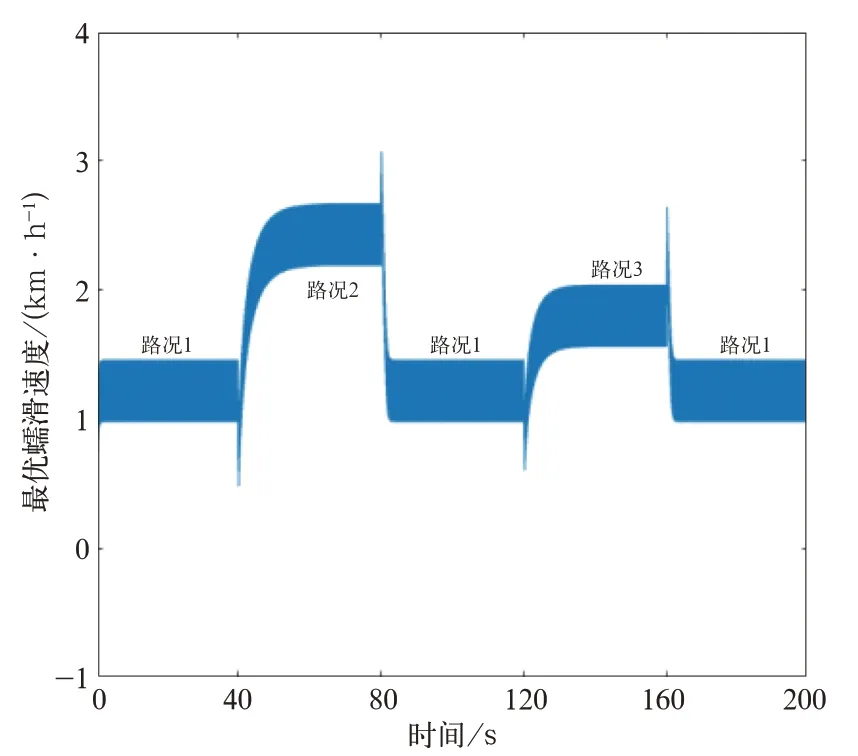
图13 滑模极值搜索方法[13]

由图14可知，列车进入路况2、路况3时，由于路况恶劣导致黏着系数较低，此时已检测到给定的转矩指令已经无法达到列车最佳运行效果，随时发生空转等故障，此时黏着控制系统迅速响应，对给定指令与控制得到的指令进行对比取小值，这样便会降低转矩，其目的是使列车适应当前路面，并工作在状态（即处于最佳最优蠕滑速度处），避免空转等情况发生。

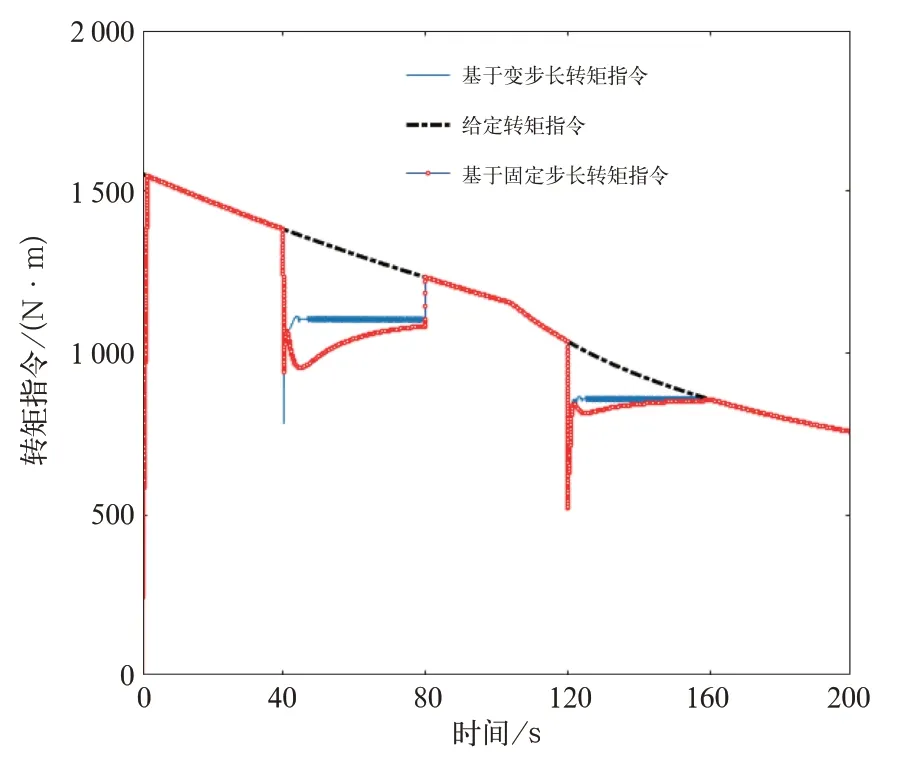
图14 转矩指令值与给定值

通过分析，基于变步长的PID控制响应效果更为稳定，且可迅速调整转矩指令既避免空转又发挥了黏着控制系统的最大潜能，稳定性较好，可以达到预期效果。基于Sigmoid函数变步长极值搜索的PID控制和固定步长极值搜索的PID控制如图15、图16所示。

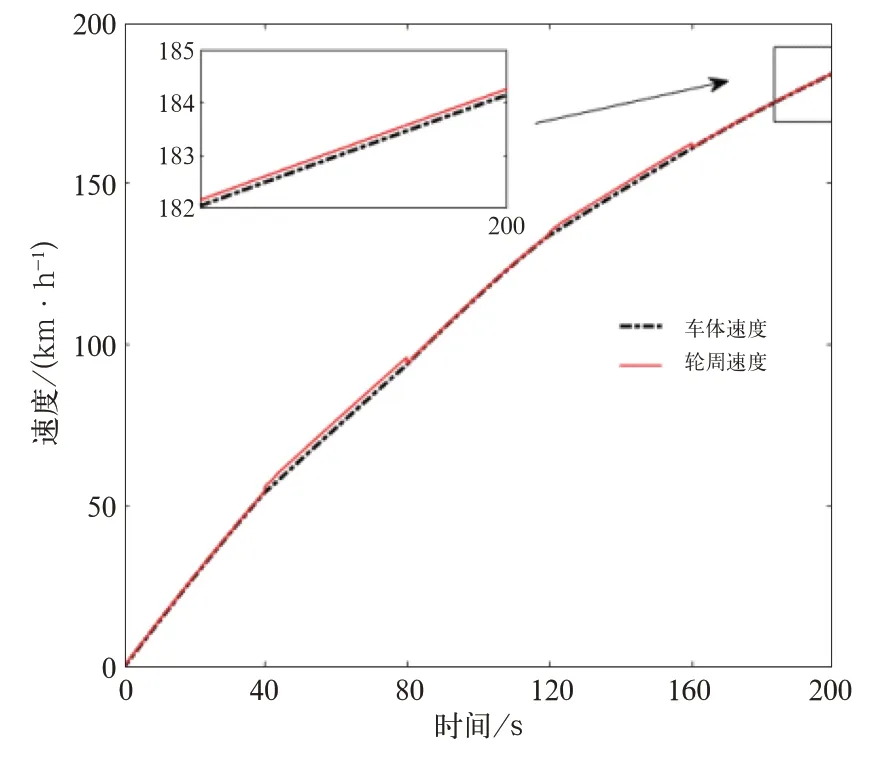
图15 基于Sigmoid函数变步长极值搜索的PID控制

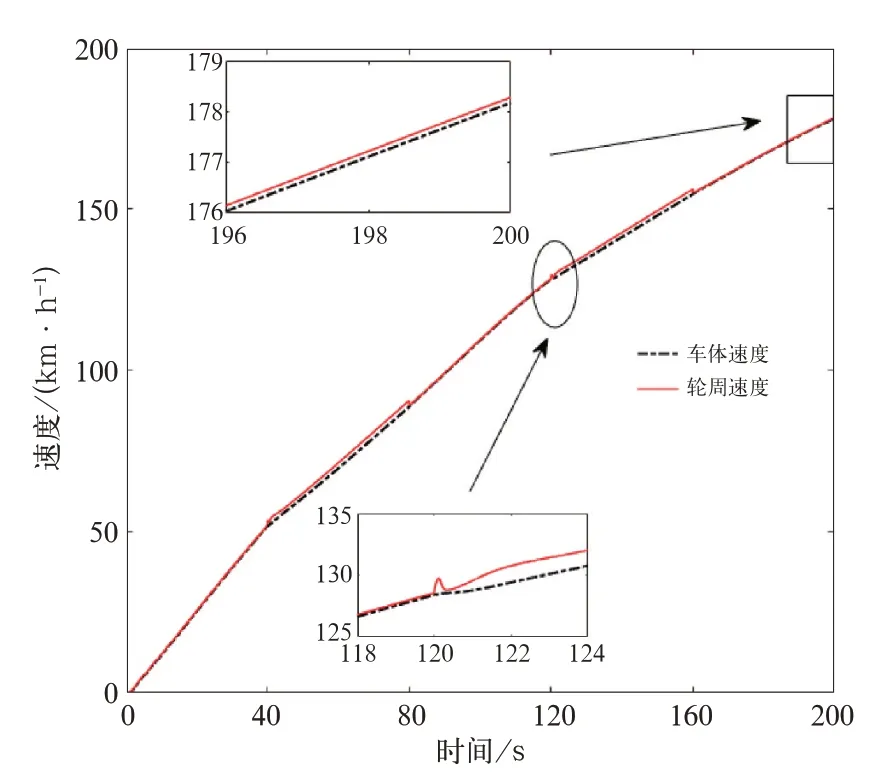
图16 基于Sigmoid函数固定步长极值搜索的PID控制

由图15、图16可知：在路况突变情况下，轮速载控制系统作用下不断搜索最佳值，并未急剧增大，由于控制系统的快速响应，也避免了列车的空转。

显然相比之下，固定步长比变步长控制系统的稳定性差，响应速度慢。同时在时间等各种参数的情况下，变步长PID所控制的车速比固定步长快7 km/h左右，且系统稳定。

6 结论

文中通过设计适合极点的全维状态观测器观测负载转矩，并采用FFRLS估算曲线斜率，提出基于Sigmoid函数改进后的变步长梯度算法搜寻出了蠕滑速度最优值，同时引入PID控制以实现最优黏着的目的。从控制效果看，在路况突变的情况下此控制方法可快速响应，并且及时搜索出最优值，结合PID控制器不但能及时地跟踪蠕滑速度的最优参考值，有效防止空转，而且能最大程度利用黏着系数，使列车牵引转矩发挥最大潜能。