四旋翼无人机前飞模态特性

叶建川，王江，梁熠，宋韬，吴则良，徐超，3

(1.北京理工大学 宇航学院，北京 100081；2.装备发展部，北京 100035；3.北京特种机电研究所，北京 100089)

0 引言

四旋翼无人机已经迅速成为民用和军用领域中最受欢迎和最为常见的无人飞行器之一[1]。四旋翼无人机具备垂直起降、悬停和巡航飞行的能力，常常用于对战场环境目标跟踪、监视、物流运输、精确农业、电力巡检、航空摄影以及无人机竞速比赛等场景[2]。随着应用需求的多样化，在旋翼无人机设计时需要考虑悬停与前飞多个飞行模态。四旋翼飞行器飞行性能的好坏在很大程度由控制器算法的效率和鲁棒性决定[3]，而控制器设计的好坏与对模型的掌握程度密切相关[4]。目前有大量的文献[1，5-9]研究了各种控制算法在多旋翼自动驾驶仪中的应用，这些控制器设计时采用了简化的多旋翼模型；模型均假设旋翼桨叶的模型参数只与转速有关。在前飞模态下，四旋翼无人机的模型与悬停时发生了较大的变化，这是因为在前飞模态下，桨叶模型发生了较大的变化[10-14]，同时机身受到的气动力也不能忽略不计；这导致了旋翼无人机在前飞时存在着严重的非线性和耦合。若采用悬停模型来描述前飞模态，会造成模型不确定性变大，对控制器设计带来不便[15]。

文献[16]通过VICON系统观察无人机的运动轨迹，结果表明随着速度的增加无人机飞行轨迹与基于悬停模型设计的期望轨迹偏差越来越大。文献[17-18]通过计算流体力学(CFD)分析了四旋翼无人机气动力，表明在前飞模态下的模型与悬停模型有着较大的差别。文献[19]采用尾迹法给出了在前飞模态下四旋翼无人机的模型，并指出在前飞模态下状态速度和姿态角变化对桨叶的拉力和阻力系数均有显著影响，但缺少对桨叶俯仰力矩和滚转力矩的分析。Remple等[20]通过风洞试验给出了多旋翼无人机前飞下的非线性模型，而该模型中缺少关键的桨叶俯仰力矩，导致模型偏差较大，难以用于控制器设计。

目前国内外关于四旋翼无人机在前飞模态的模型尚未有系统的研究。本文通过“机理建模+风洞试验”结合方法得到了四旋翼无人机在前飞模型下的动力学模型，并对前飞模态特性进行分析。无人机在前飞过程中，旋翼桨叶与悬停模态相比较，此时不仅产生一个垂直于桨叶平面的拉力和反扭矩，同时也产生阻力、俯仰力矩和滚转力矩[12，21]。本文基于叶素理论(BET)推导出旋翼桨叶在前飞模态时的模型结构，并通过风洞试验获得桨叶和机身在前飞模态下气动力，通过最小二乘法拟合得到机身和桨叶模型的模型参数，二者相结合即可得出无人机在前飞模态的气动力参数。本文通过机理分析阐述了无人机在飞行过程中阻尼力矩产生的机理。在前飞点配平并线性化，给出四旋翼无人机在前飞模态下的状态空间矩阵，详细解释每个参数的物理意义，并对存在的耦合项进行分析。最后通过飞行试验，对模型进行验证，得出开环模型与实际飞行数据之间变化趋势一致，误差在合理范围内，验证了模型的准确性。

1 无人机动力学模型

1.1 无人机受力分析

本文研究对象为“X”布局的四旋翼无人机，无人机受力如图1(a)所示，无人机主要受力部件为4个旋翼桨叶和一个机身，其中包括4个桨叶产生的拉力、阻力、侧向力、扭矩、俯仰力矩和侧向力矩以及机身受到的气动力(3个方向的力和力矩)。此外无人机在前飞时，存在阻尼力矩和桨叶旋转产生的陀螺力矩。图1(b)中，l和d分别为前后电机距离和左右电机距离的一半。

图1 无人机布局及受力分析

1.2 无人机刚体动力学模型

将无人机视为刚体，则无人机的运动学方程组[22-23]由3个力平衡方程和3个力矩平衡方程组成的飞行器6自由度欧拉方程组，以及3个姿态角和角速率运动学方程组成：

(1)

无人机动力学模型包含机体动力学和电机动力学模型，其中机体动力学模型包括机身和桨叶的动力学模型，组成如图2所示；对于多旋翼无人机，控制指令分为俯仰通道、滚转通道、偏航通道以及高度通道4个指令(俯仰控制指令δlon、滚转控制指令δlat、偏航控制指令δped、垂向控制指令δcol)。

图2 无人机动力学模型

本文将无人机动力学模型分成机体动力学和电机动力学，其中机体动力学部分由桨叶和机身组成，电机动力学由电调和电机组成(1阶环节)，本文对这三部分分别进行讨论。

1.3 桨叶气动力模型

通常在悬停模态下的无人机桨叶模型可认为只产生拉力和扭矩，而前飞模态下旋翼桨叶不仅产生拉力和扭矩，还产生俯仰力矩、滚转力矩和阻力[11-12，24]。前飞模态下桨叶所受到的气动力和气动力矩如图3(a)所示。图3(a)中：Oxyz为桨叶坐标系；Tp为垂直桨叶平面的拉力；Hp为平行于桨平面的力；Qp为桨叶的扭矩；αp为来流方向与桨平面的夹角；Fyp为侧向力；Mxp为桨叶旋转产生的滚转力矩；Myp为桨叶旋转产生的俯仰力矩；v∞为来流速度；vz为来流垂直于桨盘的速度分量；vh为来流平行于桨盘的速度分量。

图3 桨叶受力及速度分解

1.3.1 叶素模型

本文采用叶素法对桨叶进行建模，在前飞模态下，桨叶和截面叶素的速度合成如图3(b)和图3(c)所示。图3(b)和图3(c)中：φp为桨叶方位角；dr为叶素所在的截面微元宽度；dT为叶素的轴向升力；dL为叶素升力；dM为叶素俯仰力矩；dH为叶素在桨平面内的阻力；dD为叶素的阻力；ϑ为叶素的速度和成角；Θ为叶素的安装角；αs为叶素的攻角；vb为叶素的合速度；ω为螺旋桨转速。将来流速度v∞分解成平行于沿桨盘平面的vh和垂直于桨盘平面的vz.定义垂直前进比μ和水平前进比ν两个无量纲参数：

(2)

(3)

式中：R为螺旋桨半径。

推力系数CT、阻力系数CH、扭矩系数CQ、俯仰力矩系数my和滚转力矩系数mx定义如下：

(4)

(5)

(6)

(7)

(8)

式中：ρ为空气密度。

采用叶素动量法进行求解，对叶素速度分量进行分析，可得叶素的速度夹角为

(9)

叶素受到的升力、阻力和俯仰力矩分别为

(10)

(11)

(12)

式中：CL为叶素的升力系数；CD为叶素的阻力系数；CM为叶素的俯仰力矩系数；c为叶素的弦长。

1.3.2 叶素升力

截面叶素受到的力和力矩投影到桨叶坐标中，得到叶素产生的轴向升力为

dT=dLcos ϑ-dDsin ϑ≈

(13)

vx=ωr+vhcosφp代入(13)式，得

(14)

由于桨叶在旋转过程中可认为vh≪ωr，则有

(15)

叶素产生的升力可写成如下形式：

(16)

1.3.3 叶素阻力

同理，叶素阻力可写成如下形式：

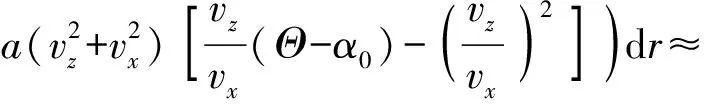
(17)

vx=ωr+vhcosφp代入(17)式中，可得

a(Θ-α0)((ωr+vhcosφp)vz))dr.

(18)

1.3.4 叶素俯仰力矩

叶素产生的俯仰力矩可写成如下表达式：

(19)

1.3.5 旋翼桨叶模型

1.3.5.1 拉力

桨叶旋转一圈产生的平均拉力为

(20)

式中：N为桨叶数量。

(13)式中叶素产生的升力代入(20)式中，可得

(21)

定积分的上下界为：r∈(0.2R，R)和φp∈(0 rad,2π rad)，可求得的拉力为

(22)

整理(22)式，则拉力Tp可写成如下形式：

(23)

式中：ζ1、ζ2、ζ3、ζ4、ζ5为拉力模型中的参数。

根据拉力系数定义和前进比的定义，可得拉力系数为

CT=t1μ3+t2μ2+t3μ+t4v2+t5，

(24)

式中：t1、t2、t3、t4、t5分别为拉力系数模型中的参数，其表达式如表1所示。

表1 ti表达式及数值

1.3.5.2 阻力

桨叶旋转一圈的阻力写成：

(25)

(18)式的dH代入(25)式中，可得

2.51a(Θ-α0)Rvhvz).

(26)

阻力可写成如下形式：

Hp=χ1vhω+χ2vhvz，

(27)

式中：χ1、χ2为阻力模型的参数。

阻力系数为

CH=h1ν+h2μν，

(28)

式中：h1、h2为阻力模型系数的参数，其表达式如表2所示。

表2 表达式

1.3.5.3 侧向力

桨叶旋转一圈的侧向力写为

(29)

积分结果为0，表明在前飞过程中桨叶产生的侧向力为0 N.

1.3.5.4 俯仰力矩

桨叶旋转一圈的俯仰力矩写为

(30)

通过将(14)式的dT和(19)式的dM代入(30)式中，进行积分求解，可得俯仰力矩为

(31)

则俯仰力矩系数可写为

my=my1ν+my2μν，

(32)

式中：mx1、mx2为滚转力矩模型的参数，其表达式如表3所示。

表3 myi表达式

(30)式积分中，dT部分积分结果为0，可知滚转力矩由桨叶在旋转时，前行桨叶和后行桨叶的叶素产生的俯仰力矩差积分所得。

1.3.5.5 滚转力矩

桨叶旋转一圈的滚转力矩写成：

(33)

通过将(14)式的dT和(19)式的dM代入(33)式中，进行积分求解，可得滚转力矩为

(34)

同理，滚转力矩系数可写为

mx=mx1ν+mx2μν，

(35)

式中：mx1、mx2为滚转力矩模型的参数，其表达式如表4所示。

表4 表达式

(33)式积分中，dM部分积分结果为0，可知滚转力矩由桨叶在旋转时，前行桨叶和后行桨叶产生的升力差产生的滚转力矩。

1.3.5.6 扭矩

桨叶旋转一圈产生的平均扭矩为

(36)

(18)式dH代入(36)式中，积分可得

(37)

则扭矩可写成如下形式：

(38)

式中：ξ1～ξ4均为与桨叶的几何参数相关为扭矩模型中的参数。扭矩系数可写为

CQ=q1μ2+q2μ+q3ν2+q4，

(39)

式中：q1、q2、q3、q4为扭矩系数模型的参数，其表达式如表5所示。

表5 qi表达式

通过(39)式可知，旋翼桨叶产生的扭矩主要由垂直前进比影响。通过上述桨叶参数模型的建立，表明旋翼桨叶的气动力系数和力矩系数只与μ和ν相关。其中模型参数(ti、qi、hi、mxi和myi)只与桨叶的几何外形(截面翼型，扭转角和弦长等)有关。

1.3.6 风洞试验验证

在风洞中进行单个旋翼桨叶的测试，模拟在实际飞行时旋翼桨叶的工作情况。通过高精度的6轴力和ME-K6D40型力矩传感器测量旋翼桨叶受到的力和力矩；通过测试电机相间交变电流的频率以及电机磁极对数来计算电机转速；通过电流电压传感器来测试电调的输入电压和电流。根据记录的参数分析旋翼桨叶在不同速度和来流角度下的性能以及对2.3节中的模型进行验证。风洞系统组成如图4所示，风洞中测试条件如表6所示。

表6 桨叶风洞试验条件

图4 桨叶风洞试验系统组成[10]

通过风洞试验得出的数据，对得出的桨叶气动力模型结构中的参数采用最小二乘法进行拟合，拟合结果如图5～图9所示。

图9 滚转力矩系数拟合结果

通过风洞试验得出的数据对1.3.2节给出的桨叶模型进行线性回归，得出拉力系数CT的模型参数如表1所示。CT拟合结果的拟合优度R2统计为0.991，均方根误差(RMSE)为1.6×10-3，表明该模型完全能描述桨叶实际模型，其中t5为悬停模态时的桨叶推力系数。从图5中可以看出，水平来流有助于提升的桨叶产生的拉力，而垂向来流降低旋翼桨叶的拉力。

图5 拉力系数拟合结果

阻力系数拟合结果如图7所示。拟合结果的R2统计为0.834，RMSE为0.86×10-3，模型能够较好地反映阻力与μ和ν的关系。通过(27)式可以看出，阻力受水平前进比ν的影响更为显著，水平来流越大，阻力越大。阻力系数及拟合参数的置信区间如表2所示。

图7 阻力系数拟合结果

扭矩系数拟合结果如图6所示。拟合结果的R2统计为0.84，RMSE为0.18×10-3.从拟合结果分析可知：CQ主要受垂直前进比μ影响；水平前进比ν对桨叶扭矩系数影响不大。扭矩系数拟合结果如表5所示。

图6 扭矩系数拟合结果

俯仰力矩系数拟合结果如图8所示。拟合结果的R2统计为0.917，RMSE为0.77×10-3，拟合效果良好。俯仰力矩系数拟合结果如表3所示。

图8 俯仰力矩系数拟合结果

滚转力矩系数拟合结果如图9所示。拟合结果的R2统计为0.866，RMSE为1.3×10-3，较好地反映了滚转力矩系数mx与垂直前进比μ和水平前进比ν的关系。滚转力矩系数拟合结果如表4所示。

1.4 桨叶阻尼力矩

四旋翼无人机绕质心运动时，桨叶旋转中心存在一个由角速率引起的线速度，从而改变桨叶垂直前进比(俯仰和滚转运动)和水平前进比(偏航运动)。

桨叶的前进比可改写为

(40)

(41)

式中：xi、yi、zi为对应的桨叶旋转中心在机体坐标系中的坐标。以旋翼产生的俯仰阻尼力矩为例，当无人机以角度率q做抬头运动时，前桨的垂直前进比增加，根据(24)式，可得前桨的产生拉力减小，同理后桨垂直比减小，拉力增加，从而产生与运动方向相反的低头力矩，前桨拉力减小部分和后桨拉力增加部分产生的力矩即为无人机俯仰阻尼力矩。结合桨叶模型和改进了后的前进比，分别对角速率求偏导即可得出无人机俯仰滚转和偏航通道的阻尼力矩系数如下：

(42)

(43)

Lr=(ω2+ω4-ω1-ω3)(my1d-mx1l)，

(44)

式中：ωi(i=1,2,3,4)为对应编号桨叶的转速。

1.5 机身气动力模型

机身在前飞过程中，受到了阻力、升力、侧向力以及3个坐标轴方向力矩的作用，如图10所示。在纵向平面内，四旋翼无人机呈几何左右对称，则无人机机身受到的侧向力、滚转力矩以及偏航力矩可忽略不计。其中机身受到的阻力与飞行速度方向一致，而升力方向垂直于速度方向，并指向地面，导致无人机在前飞过程中需要产生更多的力来维持无人机飞行状态。图10中，Mb为机身受到的俯仰力矩，Db为机身受到的阻力，Lb为机身受到的升力，Obx、Oby、Obz分别为机体系坐标系的3个方向。

图10 机身受力分析

机身的气动力计算可写为

(45)

(46)

(47)

式中：v∞为来流速度；S为机身最大截面积；cl为机身升力系数；cd为机身阻力系数；cm为机身俯仰力矩系数。

在风洞中设置不同的来流速度和机身的安装角对无人机机身模型进行吹风试验，如图11所示。

图11 机身风洞试验

试验数据采用德国Me-ßsysteme GmbH公司生产的ME-K6D40型6轴高精度力/力矩传感器进行采集。通过试验记录的数据对机身气动力模型进行拟合，得出cl、cd和cm随机身攻角变化的曲线如图12所示。进而可得出机身的气动力模型为

图12 机身气动力系数

cl=0.049 56α2-0.020 55α-0.003 925，

(48)

cd=0.080 66α2-6.757×10-5α+0.131 2，

(49)

cm=0.003 245α2+0.017 07α+0.004 454，

(50)

1.6 电机动力学

1.6.1 电机稳态模型

通常对于一架无人机的无刷直流电机控制，给定的指令是一个油门值(δthr∈(0,1)).

无刷电机等效电路图如图13所示[25]，建立电机油门与输出转速之间的关系，转速、力矩与油门之间的关系。图13中，La为电机等效线电感；ra为绕组线电阻；Ke为等效反电动势系数；Ud为直线母线电压；ie为等效电流。

图13 无刷电机等效电路图

进而可得出电压与转速、扭矩之间的关系为

(51)

Ud=δthrUbat，

(52)

式中：J为电机外壳和桨叶的转动惯量；KT为电机的电磁扭矩系数；Bv为电机的黏滞系数；Ubat为电池电压；δthr为油门值，取值范围为0～1，不考虑过渡过程，则油门值δthr与转速ω和负载Q的关系可表示为

(53)

无人机在飞行过程中，电机负载即为桨叶产生的反扭矩。根据(39)式和(50)式，转速可写为

(54)

式中：ζ=(raBv+KeKT+q2wra).

通过测试将上述参数的真实值代入(54)式中即可得出桨叶转速与状态量和输入量之间的关系。通过(54)式，可得无人机转速不仅与油门相关，还与垂直于桨叶的速度和平行于桨叶旋转平面的速度相关。在不同模态下，电机输入油门与拉力的变化曲线如图14所示。

图14 不同来流速度和来流角下桨叶拉力与油门变化关系

从图14中可以看出：在来流角度为0°时，拉力随着来流速度的增加而增大；在来流角度为15°时，拉力随着速度的增加而减小。表明旋翼桨叶拉力模型在悬停和前飞模态两种模态下相差较大。

1.6.2 电机电调模型

电机电调动力学模型可简化为一个1阶模型，通过在台架上进行扫频辨识试验，记录电机输入油门和旋翼桨叶的输出转速，如图15所示，通过辨识可得到油门输入与转速之间的关系为

图15 电机辨识扫频辨识数据

(55)

式中：s为拉普拉斯算子；0.001 3 s为电机电调的等效纯延时时间。

(2)式～(8)式、(21)式、(27)式、(29)式、(31)式、(34)式、(37)式、(40)式、(41)式～(44)式、(50)式代入(1)式中，即可得到无人机的非线性动力学模型。

2 线性化

2.1 配平点配平

无人机在稳定前飞时，无人机姿态和高度保持不变；通过建立的非线性模型可求出无人机在前飞时的平衡油门和状态变量平衡点。无人机前飞时的垂向通道和俯仰通道随前飞速度的变化如图16所示。

图16 状态量与控制量随前飞速度变化曲线

从图16中可以看出：随着前飞速度的增加，俯仰角增大；在低速下，垂向通道指令基本保持不变，无人机前飞指令主要受俯仰控制指令影响；随着速度的增加，俯仰控制指令基本不变，前飞速度指令主要由垂向指令控制。无人机以15 m/s前飞时，无人机平衡点的状态量和控制量分别为

x0=[u0,v0,w0,p0,q0,r0,φ0,θ0,ψ0]T=

[14.61 m/s, 0 m/s,-3.39 m/s, 0 rad/s,

0 rad/s, 0 rad/s, 0°,-13.068°, 0°]T，

(56)

u0=[δlat0,δlon0,δped0,δcol0]T=

[0,-0.091 6, 0, 0.347 6]T，

(57)

式中：x0为配平时的状态量矩阵，下标0表示状态和控制变量在配平点的值；u0为配平时的控制量矩阵；u0为配平点时机体系下x轴方向的速度；v0为配平点时机体系下y轴方向的速度；w0为配平点时机体系下z轴方向的速度；p0为配平时的滚转角速度；q0为配平时的俯仰角速度；r0为配平时的偏航角速度；φ0为配平时的滚转角；θ0为配平时的俯仰角；ψ0为配平时的偏航角；δlat0为配平时的滚转指令；δlon0为配平时的俯仰指令；δped0为配平时的偏航指令；δcol0为配平时的垂向控制指令。

2.2 状态空间方程

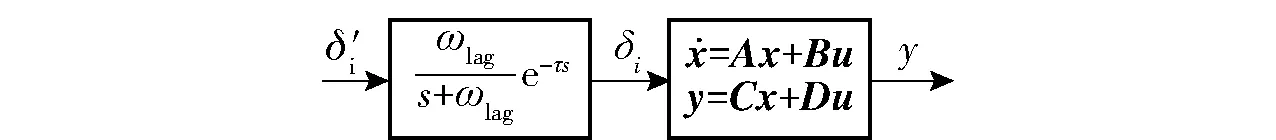
图17 等效模型

选择无人机的状态量为

x=[u,v,w,p,q,r,φ,θ,ψ]T，

(58)

无人机的状态空间方程可表示为

(59)

y=Cx+Du.

(60)

控制量输入为

u=[δlat,δlon,δped,δcol]T.

(61)

2.1节得到的非线性模型在15 m/s平衡点处线性化，得到前飞点中A、B矩阵中的参数如表7所示。

表7 模型参数物理意义

根据表7中参数的物理意义和状态量的选择，A、B矩阵分别可表示为

(62)

(63)

2.2.1 俯仰与垂向的耦合

2.2.2 滚转与偏航的耦合

从表7可以看出，偏航输入指令会造成滚转耦合，这是因为无人机在前飞时做偏航运动，对角的旋翼桨叶转速增加，另外一个对角的桨叶转速降低，此时转速增加的桨叶产生的滚转力矩增大且方向一致，转速降低的桨叶产生的滚转力矩降低且方向一致，因此产生滚转力矩，从Lped和Nped数值上看，偏航通道对滚转的耦合影响非常大。而在滚转运动时，滚转输入指令对偏航通道的耦合较小。这是由于无人机在做滚转运动时，一侧的电机转速同时增加(减少)，转速增加的一对桨叶由于旋转方向相反，产生的偏航力矩基本上可相互抵消，因此偏航运动对滚转输入指令响应很小(Llat≫Nlat)。滚转指令对偏航的耦合较小。

3 模型时域验证

3.1 模型合理性标准定义

采用开源飞控PX4在姿态模式下进行飞行试验。4个通道的控制器分别对4个俯仰、滚转、偏航和垂向4个通道进行控制，其中俯仰、滚转和偏航控制器结构采用串级PID的结构，如图18所示，其中A、B、C、D、E、F、G、H分别描述在控制器结构不同位置处的信号。

图18 控制器结构

记录无人机开环动力学的输入信号和输出信号，即图18中E、H和G处的信号。

对于数学模型，此时输入信号为

u=urecord-u0，

(64)

式中：urecord为E处记录的信号。此时模型可表示为

(65)

(66)

式中：H1和H0为状态输出矩阵；输出y包含无人机角速率、姿态角、垂向加速度和垂向速度，

(67)

ybio为常值偏移量，可通过状态估计得出。相应地，定义飞行数据的输出为

ydata=yrecord-y0，

(68)

式中：yrecord为机载传感器记录的数据；y0为配平点的输出。定义模型输入与实际飞行数据之间的均方根JRMS为

(69)

式中：nt为记录的输出通道个数；n0为每个通道中数据的个数；W为每个输出量的权重，由每个输出量的量纲决定[15]。JRMS为模型时域精度判断提供了一个有用的总体度量指标。文献[15]指出JRMS<2时，表明该模型精度在可接受范围内。

3.2 验证结果

本文机理模型的预测响应与飞行数据进行比较。前飞在平衡状态时，给定“doublet”双面脉冲激励信号，记录无人机飞行数据，并与数学模型的预测响应进行比较来评估模型的预测能力。4个主通道的时域验证曲线如图19～图22所示。

图19 俯仰通道(JRMS=0.683 0)

图20 滚转通道(JRMS=0.484 6)

图21 偏航通道(JRMS=0.766 7)

图22 高度通道(JRMS=0.668 8)

4个通道的JRMS均小于1，满足指标要求，表明该模型具有较高的精度，可高保真度地描述无人机前飞时的动力学特性。

4 结论

本文给出了在前飞模态下桨叶的广义数学模型，并通过风洞试验进行验证，分析了该桨叶模型的不确定性。建立无人机的动力学方程，得出无人机在前飞模态的状态空间方程，并分析解释了在前飞时无人机动力学特性，以及前飞时通道之间的耦合。

通过飞行试验对该模型进行验证，结果表明该模型与飞行数据的轨迹基本一致，验证了该模型的准确性。为下一阶段的控制设计奠定了良好基础。

参考文献(References)

[1] AMEZQUITA-BROOKS L，LICEAGA-CASTRO E，GONZALEZ-SANCHEZ M，et al.Towards a standard design model for quadrotors: a review of current models，their accuracy and a novel simplified model[J].Progress in Aerospace Sciences，2017，95:1-23.

[2] SAEED A，YOUNES A B，CAI C，et al.A survey of hybrid unmanned aerial vehicles[J].Progress in Aerospace Sciences，2018，98:91-105.

[3] PINES D J，BOHORQUEZ F.Challenges facing future micro-air-vehicle development[J].Journal of Aircraft，2006，43(2):290-305.

[4] BRISTEAU P J，MARTIN P，SALAÜN E，et al.The role of propeller aerodynamics in the model of a quadrotor UAV[C]∥Proceedings of the 2009 European Control Conference.Budapest，Hungary:IEEE，2009:683-688，

[5] JIANG T，LIN D F，SONG T.Finite-time backstepping control for quadrotors with disturbances and input constraints[J].IEEE Access，2018，6:62037-62049.

[6] AMEZQUITA-BROOKS L，HERNANDEZ-ALCANTARA D，SANTANA-DELGADO C，et al.Improved model for micro-UAV propulsion systems:characterization and applications[J].IEEE Transactions on Aerospace and Electronic Systems，2020，56(3):2174-2197.

[7] HOFFMANN G M，HUANG H M，WASLANDER S L，et al.Quadrotor helicopter flight dynamics and control:theory and experiment[C]∥Proceedings of the AIAA Guidance，Navigation and Control Conference and Exhibit.Hilton Head，SC，US:AIAA，2007:6461.

[8] 吕品，赖际舟，杨天雨，等.基于气动模型辅助的四旋翼飞行器室内自主导航方法[J].航空学报，2015，36(4):1275-1284.

LÜ P，LAI J Z，YANG T Y，et al.Autonomous navigation method aided by aerodynamics model for an indoor quadrotor[J].Acta Aeronautica et Astronautica Sinica，2015，36(4):1275-1284.(in Chinese)

[9] 夏青元，徐锦法.三轴式无人旋翼飞行器及自适应飞行控制系统设计[J].航空学报，2013，34(3): 495-508.

XIA Q Y，XU J F.A design of triaxial unmanned rotor aircraft and its adaptive flight control system[J].Acta Aeronautica et Astronautica Sinica，2013，34(3): 495-508.(in Chinese)

[10] YE J C，WANG J，HE S M，et al.Rotor performance analysis and modeling of multirotor using wind-tunnel test[C]∥Proceedings of the 2020 International Conference on Unmanned Aircraft Systems.Athens，Greece: IEEE，2020:1644-1649.

[11] THEYS B，DIMITRIADIS G，HENDRICK P，et al.Experimental and numerical study of micro-aerial-vehicle propeller performance in oblique flow[J].Journal of Aircraft，2017，54(3):1076-1084.

[12] KOLAEI A，BARCELOS D，BRAMESFELD G.Experimental analysis of a small-scale rotor at various inflow angles[J/OL].International Journal of Aerospace Engineering，2018[2020-11-25].https:∥doi.org/10.1155/2018/2560370.

[13] HWANG J Y，JUNG M K，KWON O J.Numerical study of aerodynamic performance of a multirotor unmanned-aerial-vehicle configuration[J].Journal of Aircraft，2015，52(3): 839-846.

[14] ORSAG M，BOG S.Influence of forward and descent flight on quadrotor dynamics[J/OL].Recent Advances in Aircraft Technology，2012:141-156[2020-11-25].https:∥www.intechopen.com/books/recent-advances-in-aircraft-technology/influence-of-forward-and-descent-flight-on-quadrotor-dynamics.

[15] TURPIN M，MICHAEL N，KUMAR V.Trajectory design and control for aggressive formation flight with quadrotors[J].Autonomous Robots，2012，33:143-156.

[16] BARCELOS D，KOLAEI A，BRAMESFELD G.Aerodynamic interactions of quadrotor configurations[J].Journal of Aircraft，2020，57(1):1-17.

[17] MISIOROWSKI M，GANDHI F，OBERAI A A.Computational study on rotor interactional effects for a quadcopter in edgewise flight[J].AIAA Journal，2019，57(12):5309-5319.

[18] LUO J L，ZHU L F，YAN G R.Novel quadrotor forward-flight model based on wake interference[J].AIAA Journal，2015，53(12):3522-3533.

[19] KAYA D，KUTAY A T.Aerodynamic modeling and parameter estimation of a quadrotor helicopter[C]∥Proceedings of the AIAA Atmospheric Flight Mechanics Conference.Atlanta，GA，US:AIAA，2014: 2558.

[20] REMPLE R K，TISCHLER M B.Aircraft and rotorcraft system identification[M].2nd ed.Blacksburg，VA，US:A IAA，2006:433-450.

[21] DROANDI G，GIBERTINI G，GRASSI D，et at.Proprotor-wing aerodynamic interaction in the first stages of conversion from helicopter to aeroplane mode[J].Aerospace Science and Technology，2016，58:116-133.

[22] PADFIELD G D.Helicopter flight dynamics including a treatment of tiltrotor aircraft[M].3rd ed.Hoboken，NJ，US:John Wiley & Sons Inc.，2018.

[23] 宋保维，张姜军，杜晓旭，等.四旋翼碟形自主水下航行器运动方程建立与流体特性仿真研究[J].兵工学报，2016，37(2):299-306.

SONG B W，ZHANG J J，DU X X，et at.Estimation of equation of motion of four-rotor dish-shaped AUV and simulation research on its hydrodynamic characteristics[J].Acta Armamentarii，2016，37(2):299-306.(in Chinese)

[24] THEYS B，DIMITRIADIS G，ANDRIANNE T，et al.Wind tunnel testing of a VTOL MAV propeller in tilted operating mode[C]∥Proceedings of the 2014 International Conference on Unmanned Aircraft Systems.Orlando，FL，US:IEEE，2014: 1064-1072.

[25] 薛晓明，杨长江.无刷直流电机建模研究[J].电机与控制学报，2009，13(6):874-885.

XUE X M，YANG C J.Study of modeling for brushless DC motor drives[J].Journal of Motor and Control，2009，13(6):874-885.(in Chinese)