爆炸反应装甲作用场下近炸引信作用距离计算模型

唐辉，焦志刚，赵东志，赵丽俊，，朱小平

(1.沈阳理工大学 装备工程学院，辽宁 沈阳 110159；2.北方华安工业集团有限公司，黑龙江 齐齐哈尔 161000)

0 引言

现今，主战坦克大多数都披挂了爆炸反应装甲[1-2]。如何有效地规避爆炸反应装甲的爆炸作用场并有效毁伤坦克装甲目标成为一个研究热点。为此，世界各国研究人员都在引信和战斗部配合方式上进行创新。

在以身管武器为发射平台的反坦克弹药中，破甲弹需要解决近炸引信与串联式聚能装药战斗部之间的引战配合问题。样机设计初期，没有可供参考的射表，因此，推算一级近炸引信作用距离的理论参考值尤为关键[3]。为了解决这一问题，本文运用低伸弹道的西亚切近似分析解法解算弹道[4-5]，得到弹道各点的弹丸速度v，建立计算模型，推出极限交会距离L，进而推导出引信作用距离S与弹速v的关系，求出在弹道各点的一级引信最佳作用距离。计算模型解出的各组S-v解析值以数据表形式被写入引信发火控制系统算法，近炸引信可根据装甲目标特性的差异调用不同弹目交会条件下的S-v数据表，以实现其作用距离的动态自适应控制，提高弹药的毁伤效率。

1 低伸弹道的西亚切近似解法推导

经典外弹道学给出了自然坐标系下以飞行时间t为自变量、以速度v运动的弹丸质心运动方程组，对于射角φ0≤5°的低伸弹道，忽略重力加速度的影响，并令ds=vdt，s为弹道孤长，则有弹丸质心运动方程组简化如下：

(1)

(2)

(3)

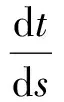
(4)

(5)

式中：c为弹道系数；Hτ(y)为空气密度函数，τ为虚温；G(vτ)为阻力函数，vτ为地面标准虚温条件下的速度；y为弹道高；φ为弹道倾角；x为水平弹道长；τs为虚温地面标准值。

D(vτ)-D(vs)=cH(y0)x，

(6)

2 计算模型建立

典型坦克炮用串联式战斗部破甲弹为长鼻形两级破甲战斗部串联结构，根据其破甲作用机理，弹丸需要避开爆炸反应装甲的反击弹射流[6-9]。

固定反应装甲位置，反击弹射流轨迹相对安装位置也固定。目标各参数不变时，破甲弹瞄准反应装甲有效区的最上沿时具有极限作用距离，即此时弹丸头部与目标之间取得极限交会距离。

2.1 极限交会距离计算

爆炸反应装甲内置钝感炸药夹层和多发不同斜置角的聚能装药反击弹，用以形成反击弹射流带，扩大对来袭弹药的毁伤区域[10-12]。其基本结构如图1所示。反应装甲斜置倾角θ、钝感炸药夹层与反应装甲背板夹角γ、反击弹支座与钝感炸药夹层夹角β及反击弹射流带右边界出射角α之间的关系为

图1 爆炸反应装甲结构示意图

α=90°-θ-γ-β.

(7)

对于弹径为D的二级串联式战斗部破甲弹，二级战斗部被反击弹击中损毁即可认定为弹丸丧失毁伤效能。根据推算，一级战斗部击中反应装甲有效区的最上沿时为极限情况，图2所示为主射流击中点即为反应装甲有效区的最上沿。

图2 弹目交会临界点示意图

图2中，D1为一级战斗部射流穿孔与反击弹射流穿孔之间的高度差，L为极限交会距离(即极限交会处弹丸肩部与反应装甲的距离)，L1为面板穿孔与弹丸肩部水平距离，H1为反应装甲面板两端边界点之间高度差，H2为反击弹射流穿孔与面板右端边界点之间高度差，H3为一级战斗部射流穿孔与面板左端边界点之间高度差。

此时，弹轴线与反击弹在反应装甲面板上的穿孔位置垂直高度为

D1=H1-H2-H3.

(8)

根据图2所示破甲弹与反应装甲反击弹射流交会的临界位置示意图，可得

L1=(D/2+D1)/tanα，

(9)

L=L1+D1/tanθ.

(10)

需要说明的是，对于不同的坦克装甲目标，其首上装甲的倾角也不同。根据(10)式可知L=L(L1，D1，θ)，θ为变量之一，爆炸反应装甲设置不同的倾角时，可得到与之对应的新的极限交会距离L，从而使得本文建立的计算模型具备普遍适用性。

2.2 引信作用距离计算

一级近炸引信采用定距发火起爆一级战斗部，不同弹道长对应不同的引信作用距离，但对于某一时刻，炮目距离是一定的，则由(6)式可算出x处弹丸速度v，以用于建立计算模型中各参数之间的关系式。

一级战斗部作用从引信探测装置提供起爆信号开始，一级战斗部形成射流、一级战斗部射流飞行至目标、射流击爆反应装甲、反应装甲反击弹射流形成，此过程弹目运动模型如图3所示。图3中：t1为一级战斗部射流形成时间；t2为一级战斗部射流到达反应装甲时间；t3为一级战斗部射流到达反应装甲时到反应装甲被击爆时间(由实验测得)；t4为反击弹射流形成时间；t5为反击弹射流到达弹丸肩部时间。

图3 弹目运动模型

根据以上引战作用过程，一级近炸引信作用距离公式推导如下：

S=L-L2+v(t1+t2+t3+t4+t5)，

(11)

(12)

v2=v+vs，

(13)

(14)

式中：L2为弹丸头部至弹丸肩部距离；X为反击弹射流飞至弹丸肩部距离；vs为一级战斗部静态射流速度，由实验测得；vd为一级战斗部动态射流速度；vh反应装甲反击弹头部射流速度，由实验测得)

坦克炮射破甲弹的有利炸高一般为3～5倍装药直径，其值小于极限交会距离L，为保证侵彻威力，二级主战斗部必须采取延时起爆方式运动到小于临界值L的范围内侵彻主装甲。因此，必须保证二级主战斗部飞至L处时反击弹射流已经越过弹丸肩部。图2中，当弹目处于极限交会状态时，反击弹射流带右边界的射流刚好越过弹丸肩部。随着弹丸继续行进，由于反击弹射流速度远大于弹丸速度，处于射流带左侧的射流也已全部越过弹肩。因此，反击弹射流不与弹丸交会的临界条件为

X·cosα>L1.

(15)

此处反击弹在反应装甲盒内的行进距离极小，可忽略。将(12)式～(15)式代入(11)式，即可推出以弹丸速度v为自变量、一级引信作用距离S为因变量的关系式F(v，S)=0.其中S与v并非呈一次线性关系，而是正相关关系。

坦克炮破甲弹的常用作战距离一般在1 000 m以内，通过以上理论计算方法，以某型破甲弹(1 000 m处着速为700 m/s)为例，推导出极限交会距离分别为1.27 m和1 000 m内一级近炸引信的理论作用距离与弹丸速度的对应关系如图4所示。

图4 引信作用距离—弹速图

从图4中可以看出，在保证极限交会距离的前提下(即反击弹射流刚好越过弹丸肩部)，S与v呈正相关关系。当弹丸飞至距炮口x1处时，v1=895 m/s，S1=1.85 m，即在一级近炸引信发火控制系统写入算法时，应保证弹速为895 m/s，一级引信在距反应装甲1.85 m处开始发火。弹丸在全弹道作变加速度的减速运动，当飞至距炮口x2处时v2=700 m/s，S2=1.67 m，即当引信在弹速为700 m/s时察觉到目标，应保证引信在距反应装甲1.67 m处开始发火。弹速越高的作用点，一级近炸引信的作用距离应当越远。

2.3 射流失稳计算

除考虑极限交会条件下弹目运动的几何关系外，反击弹射流的拉伸状态也需加以分析。聚能射流具有很高的头部速度和较低的尾部速度，大炸高下射流长度不断延伸，当射流失稳断裂，射流粒子会发生偏离、飞散和翻转，其侵彻能力会显著下降[13-15]。

射流断裂时间tc计算公式为

(16)

式中：lc为射流颈缩长度；li为射流初始长度；vt为射流尾部速度。

当模型处于弹目交会临界点时，t5>tc，反击弹射流已经发生断裂处于失稳状态，必然会出现射流溅射等情况，其侵彻能力大幅减弱，此时可认为对有一定厚度弹体保护的主战斗部聚能装药基本无威胁。

3 试验验证

为验证L临界值的合理性，对爆炸反应装甲进行目标特性分析，并根据一级战斗部作用距离理论计算值，布置爆炸反应装甲威力场静态验证试验，共设置6组不同的弹丸与反应装甲距离L，对不同距离上的反应场威力进行验证。试验布置及试验效果如图5、图6所示。

图5 试验布置情况

图6 验证试验效果图

采集数据并对数据进行分析，得到详细试验数据结果如表1所示。

从表1中可以看出：当设置不同的弹丸与反应装甲距离L，随着L增大，威力场逐渐减弱，反击弹对目标的毁伤效果降低；当L增大到1.2 m时，反击弹射流穿深仅为3 mm，且溅射范围大。

表1 爆炸反应装甲威力场试验结果

4 结论

为提高爆炸反应装甲作用场下的引战配合效能，本文针对串联战斗部破甲弹的近炸引信作用距离问题，利用低伸弹道的西亚切近似解法解算弹道，进而建立了近炸引信作用距离的理论计算模型，并通过试验对计算模型的合理性进行了验证。得到如下主要结论：

1)经爆炸反应装甲威力场静态试验验证：当L≤0.8 m时，反击弹威力场集中，其对来袭目标毁伤效果极强；当0.8 m1.2 m时，反击弹射流穿深应小于3 mm，由于破甲弹丸本身弹壁有一定厚度，所以此时可认为反击弹的威胁基本消除，可认定L=1.2 m为安全临界值。

2)每个S值都是基于L值推导而来，依据理论计算模型导出的L=1.27 m，与验证试验得到的安全临界值1.2 m基本吻合，因此，在此基础上，依据本文方法建立的计算模型推导出的1 000 m内一级引信作用距离S的理论计算值合理可行。采用低伸弹道发射的近炸引信弹药引战配合参数理论值的设计可参考此模型。

参考文献(References)

[1] 曹贺全，张广明，孙素杰，等.装甲车辆防护技术研究现状与发展[J].兵工学报，2012，33(12):1549-1554.

CAO H Q，ZHANG G M，SUN S J，et al.Status and development of protection technology of armored vehicles[J].Acta Armamentarii，2012，33(12):1549-1554.(in Chinese)

[2] 房凌晖，郑翔玉，马丽，等.坦克装甲车辆装甲防护发展研究[J].四川兵工学报，2014，35(2):23-26.

FANG L H，ZHENG X Y，MA L，et al.Armor protection development of tank & armored vehicle[J].Journal of Sichuan Ordnance，2014,35(2):23-26.(in Chinese)

[3] 田博，施坤林，邹金龙，等.近炸引信炸点对弹药毁伤评估的影响[J].探测与控制学报，2020，42(6):1-7，12.

TIAN B，SHI K L，ZOU J L，et al.Fuze explosion point effect on ammunition damage assessment[J].Journal of Detection & Control，2020，42(6):1-7，12.(in Chinese)

[4] 刘鹏，王雨时，闻泉，等.超音速弹丸低伸弹道的近似解析解[J].探测与控制学报，2016，38(4):42-46，51.

LIU P，WANG Y S，WEN Q，et al.Approximate analytical expression of supersonic projectile low trajectory[J].Journal of Detection & Control，2016，38(4):42-46，51.(in Chinese)

[5] 王连敏.低速低伸弹道解法[J].兵工学报，1981，2(1):11-18.

WANG L M.A solution of the low-speed and flat trajectory[J].Acta Armamentarii，1981，2(1):11-18.(in Chinese)

[6] 黄鹤，陈建申，徐鹏，等.破甲反击弹抗串联战斗部的可行性[J].兵工自动化，2019，38(8):55-57.

HUANG H，CHEN J S，XU P，et al.Feasibility of anti-series warhead of HEAT counter-attack projectile[J].Ordnance Industry Automation，2019，38(8):55-57.(in Chinese)

[7] 郎明君，徐学华.多级串联聚能装药隔爆时间的计算与测试[J].南京理工大学学报，2002，26(6):625-627，631.

LANG M J，XU X H.Calculation and test on flame-proof time of multistage-series shaped charge[J].Journal of Nanjing University of Science and Technology，2002，26(6):625-627，631.(in Chinese)

[8] 史志鑫.串联毁伤元对斜置反应装甲目标的侵彻性能研究[D].太原：中北大学，2020.

SHI Z X.Research on the penetration performance of tandem damage element to oblique reaction armor target[D].Taiyuan：North University of China，2020.(in Chinese)

[9] 万清华.多三明治结构反应装甲干扰射流作用研究[D].太原：中北大学，2019.

WAN Q H.Interference effect of reactive armor with multi-sandwich on shaped charge jet[D].Taiyuan：North University of China，2019.(in Chinese)

[10] 万清华，李如江，杨玥，等.多三明治结构反应装甲干扰射流的数值模拟[J].高压物理学报，2018，32(6):123-130.

WAN Q H，LI R J，YANG Y，et al.Numerical simulation of interference effect of multi sandwich structure reaction armor to jet[J].Chinese Journal of High Pressure Physics，2018，32(6):123-130.(in Chinese)

[11] 张乐.某结构反应装甲对射流干扰的机理研究[D].南京：南京理工大学，2016.

ZHANG L.Research on the interferences principle of the ERA to jets[D].Nanjing：Nanjing University of Science and Technology，2016.(in Chinese)

[12] 熊良平，黄道业，王凤英.新型反应装甲结构对长杆弹小法线角侵彻的干扰分析和防护效能[J].爆炸与冲击，2013，33(1):108-112.

XIONG L P，HUANG D Y，WANG F Y.Protection effectiveness of a new explosive reactive armor against penetration of long-rod projectiles with small yaw angles[J].Explosion and Shock Waves，2013，33(1):108-112.(in Chinese)

[13] 石艺娜，秦承森.金属射流失稳断裂的理论分析[J].力学学报，2009，41(3):361-369.

SHI Y N，QIN C S.Instability and breakup of stretching metallic jets[J].Chinese Journal of Theoretical and Applied Mechanics，2009，41(3):361-369.(in Chinese)

[14] 黄正祥.聚能装药理论与实践[M].北京:北京理工大学出版社，2014.

HUANG Z X.Theory and practice of shaped charge[M].Beijing:Beijing Institute of Technology Press，2014.(in Chinese)

[15] 王树山.终点效应学[M].北京:科学出版社，2019.

WANG S S.Terminal effects[M].Beijing:Science Press，2019.(in Chinese)