燃料空气炸药二次起爆引信与爆轰云雾动态交会浓度检测方法

吉童安，娄文忠，付胜华，汪金奎，刘伟桐

(1.北京理工大学 机电学院，北京 100081；2.北京理工大学 重庆创新中心，重庆 401120)

0 引言

爆轰物理学表明：燃料空气炸药(FAE)抛撒存在浓度爆炸极限和最佳起爆浓度，只有在浓度爆炸极限范围内，才能发生云雾爆轰；在最佳起爆浓度条件下，才能产生最大爆轰速度、最大爆压和最高温度，实现充分爆轰[1-3]。对于落速不同的FAE，弹体落速越高，交会时间越早，交会时间窗口越短，0 m/s落速的交会时间窗口约为39 ms，510 m/s的交会时间窗口约为17 ms[3].高速引信与云团交会时间窗口内实现对爆炸云团浓度的快速响应与起爆是制约FAE爆轰威力的关键技术瓶颈。

FAE抛撒形成云雾主要为气态/燃料颗粒两相混合物，在现有检测技术中，主要有光散射原理法和静电感应方法，Yamazaki等[4]和Omotayo等[5]通过光学传感器构建检测系统，实现了云团浓度的识别。然而，光学管路易堵塞、光学窗口易污染，需要对传感器进行频繁维护；静电感应传感器根据粉尘的静电特性，在不同浓度下的电荷量解算浓度，未能实现浓度特征信息的提取，由于静电效应，外界静电会对传感器探测产生干扰，且静电累计不能实时释放，暂时未能实现粉尘浓度的实时动态测量。

当前声波在混合物中的衰减模式和机理已经较为清晰，早在20世纪60年代，Lloyd和Berry就推导出了超声在颗粒介质中的散射模型[6]。美国Los Alamos国家实验室[7]试验证明通过检测声波复波数方式可以同步获得声速变化和声衰减现象，对两种声波特征进行相关测试分析，可以获得更多多相混合物的特征数据，实现浓度和颗粒粒径分布同时检测。乔榛[8]采用试验的方法测定煤粉的部分物性参数，利用已有的超声传播衰减理论模型对超声波在空气-煤粉两相介质中传播的速度和衰减进行数值计算，分析了物性参数对计算结果的影响；郭盼盼等[9]采用蒙特卡罗方法预测不同粒度、浓度及超声频率下玻璃微珠/水颗粒两相体系中颗粒的超声衰减特性，建立颗粒表征模型；郭明儒等[10]、Fu等[11-12]和付胜华等[13]提出利用超声波在云雾介质中传播时能量的衰减和相位变化的特性动态实时测量云雾浓度，通过建立超声波传播衰减与云雾浓度的对应关系，建立超声在云雾介质中传播的衰减模型，从而获取一种动态云雾浓度快速检测方法。

本文采用数值模拟的方法，考虑了引信与FAE云雾场在100 m/s速度交会时，引信浓度检测流道内云雾颗粒和风流混合流动形成的气体与固体(简称气固)两相流体的流动规律，以及在气固两相流动的湍流效应下浓度场的建立过程及分布规律，验证了超声波在探测云雾场时衰减特性与粉尘浓度的对应关系，证实了利用超声在云雾中传播衰减的浓度探测可行性。

1 试验样机与测试平台

云雾动态浓度检测引信样机如图1所示，预留2对传感器安装位置，用以安装超声传感器，超声传感器栅孔相对安装，朝向内流道方向。样机前端开设云雾入口，后端开设云雾出口，内流道尽量避免截面突变和流动死区保证流道均匀通畅。

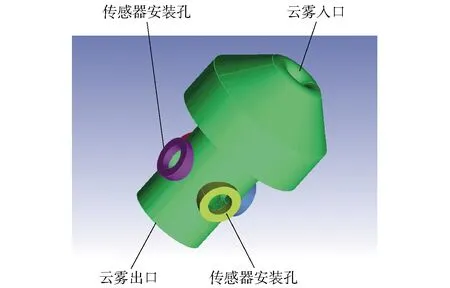
图1 引信样机

为了模拟引信与燃料云雾场的高速交会环境，验证传感器的高动态响应及衰减特性，试验平台选用火箭撬平台，通过设定不同引信-云团交会环境浓度，获得动态云团浓度信息，实现模拟真实环境下引信-云团高速交会，获得可靠的引信探测云团浓度的动态特性。

引信浓度检测样机安装在火箭撬平台上，设计引信以100 m/s的速度穿过云团。在标准1.5 m×1.5 m×1.5 m箱体内产生标称浓度(云雾颗粒在标准体积内均匀分散)分别为75 g/m3、150 g/m3、225 g/m3的等效FAE抛撒云团。试验现场如图2所示。

图2 试验现场

2 云雾场计算模型及参数计算

云雾场属于典型的气固两相流，本文选用离散粒子模型，基于欧拉-拉格朗日方程，将气相处理为连续相，燃料为颗粒离散相，考虑气固两相流系统中颗粒运动的特点，该模型对颗粒在两相流中的运动过程进行了分解，即由冲击力控制的瞬时碰撞运动和由流体曳力控制的悬浮运动，从而建立了粒子运动的分解模型[14-15]。在欧拉坐标系下建立Navier-Stokes方程求解其流动、传热和反应特征。同时进行计算域中的每个离散颗粒的运动轨迹，来反映整个离散场。

2.1 气相流动控制方程

在气固两相流的研究中，引入连续相孔隙率αf，表示控制体中气体所占的体积份额[14]，即

(1)

式中：Vt,i为控制体中第i相颗粒的总体积；V为控制体的体积。

连续性方程为

(2)

二维截面动量守恒方程为

(3)

式中：uxi、uxj分别为xi轴、xj轴方向上的速度(m/s)；p为气体压力(Pa)；τij为黏性应力(Pa)；f为颗粒与流体之间的相互作用，与二者之间的速度有关；g为重力加速度(m/s2)。

本文研究的燃料云雾气固两相流中，气体是一种无序状态的湍流，计算时选择标准k-ε方程。

2.2 离散相控制方程

根据牛顿第二定律，颗粒相的运动求解方程为

(4)

(5)

式中：m为颗粒质量(kg)；v为颗粒运动速度(m/s)；F为流体作用于颗粒的流体力(N)；Ip为颗粒的转动惯量(kg·m2)；w为颗粒的角动量(kg·m/s)；M为作用于颗粒上的转矩(N·m)。

流场内部为充分发展的湍流，需要在气流入口添加湍流强度和水力直径来表征流场流动特征，湍流强度和水力直径按照(6)式～(8)式进行计算：

(6)

(7)

式中：I为湍流强度；Re为雷诺数；ρa为空气的标准密度(kg/m3)；u为风流进入流场速度(m/s)；d为水力直径(m)，

(8)

S为流动横截面面积(m2)，l为流动横截面周长(m)；μ为空气的动力黏度(Pa·s)。

本文中，引信样机内流道直径为0.1 m，由(8)式计算得到水力直径为0.2 m.在空气标准密度为1.293 kg/m3、压强为101.325 kPa、温度为20 ℃条件下，空气动力黏度为17.9×10-6Pa·s，火箭撬推进末端的运动速度为100 m/s，计算得湍流强度为2.72%.

3 数值模拟步骤及参数设置

利用计算流体动力学(CFD)软件对引信样机进行流道抽取，网格划分和边界定义，在有限元分析软件Ansys Fluent中读入包含网格信息和边界信息的网格文件，检查并汇报网格质量，防止有负体积的网格发生，以免仿真过程中方程解出现无法迭代收敛错误[16-17]，如图3所示，其中in为速度入口，out为自由出流。

图3 引信样机内流道模型及有限元划分

假设流场内气固两相流体为不可压缩流体，选择基于压力的求解器，选择瞬态求解模型，求解器设置参数如表1所示。

表1 Fluent求解器设置

设置离散相颗粒直径为1×10-6m，初始质量流率为0.01 kg/s，喷射方式为面喷射，从入口射入，方向垂直于设定面，初始速度为100 m/s；材料密度为2 719 kg/m3(铝粉)，假设颗粒均为均匀的球体，忽略颗粒体积变化，设置离散相与连续相间的耦合，计算模型的全部参数设置如表2所示。

仿真中离散粒子从入口均匀吹入，入风方向与入口垂直，入口边界条件为速度入口边界条件，出口为自由出流。设定入风速度为100 m/s，设定入口出的湍流强度和水力直径。其他边界的流动属性相关标量如表3所示。

表3 边界条件设定

设置求解算法为SIMPLE算法，由于箱体长度为1.5 m，交会速度为100 m/s，交会时间为0.015 s，故初始化流场后设置迭代步长为0.00 01 s，迭代步数200步，仿真时长为0.02 s.

4 模拟仿真与试验结果验证

4.1 模拟结果

内流道为直径0.1 m的圆柱，设定穿过云雾浓度分别为75 g/m3、150 g/m3、225 g/m3的云雾箱时，对应的固相粒子的质量流率分别为0.058 9 kg/s、0.117 8 kg/s、0.176 7 kg/s，对此3种情况进行仿真，表4分别表示了气相速度为100 m/s，固相粒子质量流率分别为0.058 9 kg/s、0.117 8 kg/s、0.176 7 kg/s情况下，流场内固相浓度的扩散和建立过程。仿真结果显示：1)当流场达到充分发展的湍流态时，超声传播路径的最大云雾浓度分别为72.5 g/m3、130 g/m3和220 g/m3，即认为此时对应超声最大衰减；2)由流场扩散过程可知，从开始到2 ms过程中，样机内流道流形完全形成，即在样机穿出云雾场前，样机流道内两相流形完全形成，流道内浓度最接近预设环境浓度。表5所示为不同质量流率对应的最大仿真浓度。

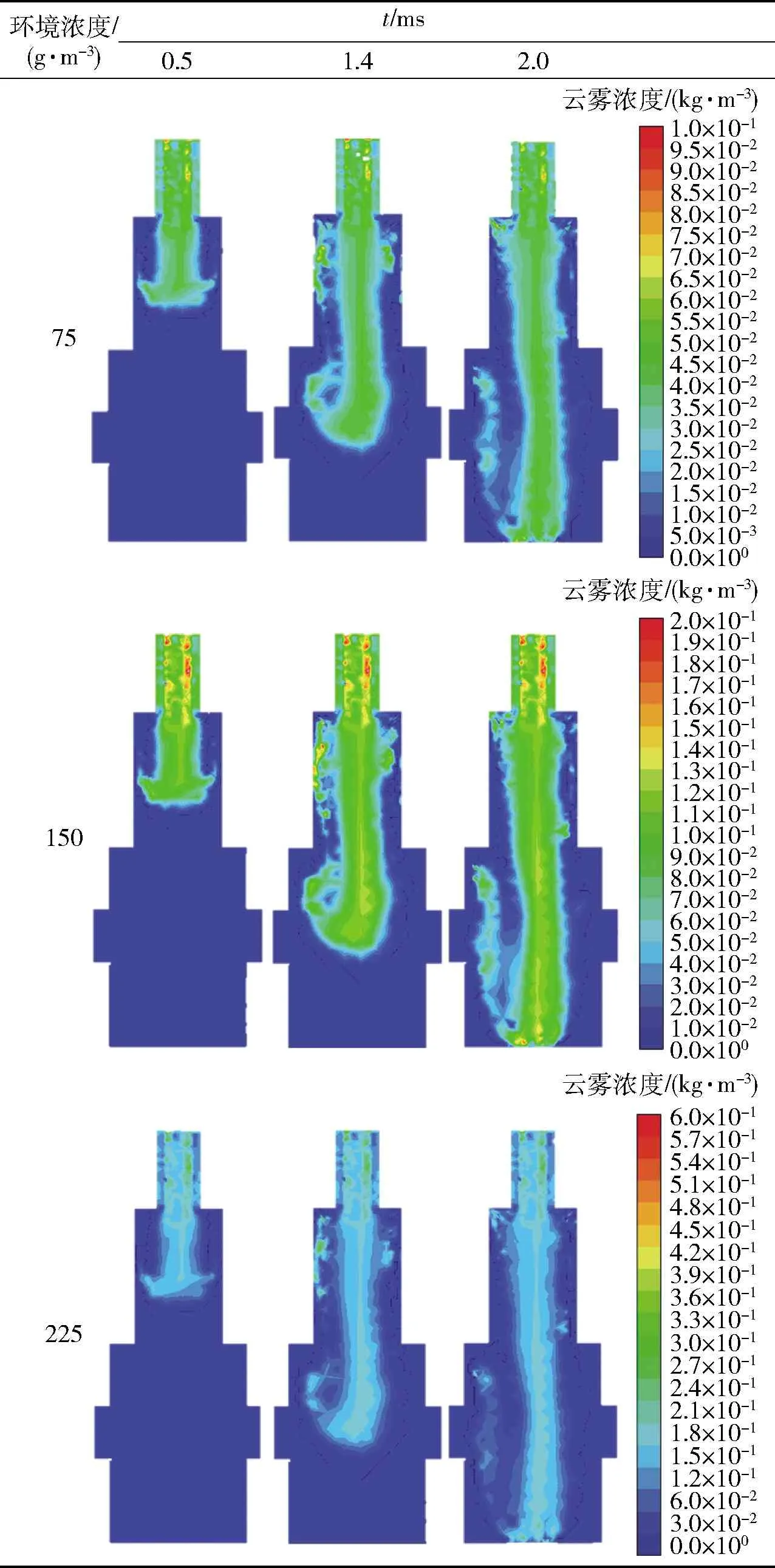
表4 引信穿过不同浓度云雾场的浓度建立过程

表5 不同质量流率对应的最大仿真浓度

4.2 试验结果

一次测试的超声回波衰减曲线如图4所示，图4中采样频率为2 MHz，两个信号尖峰为穿越箱体时的震动噪声。两个尖峰中间对应着在云雾场中超声的回波信号即为衰减值，两个尖峰外侧则对应着普通环境中的超声回波，记为平稳值。则脉冲超声在云雾场中超声衰减率计算为：衰减率=1-衰减值/平稳值。

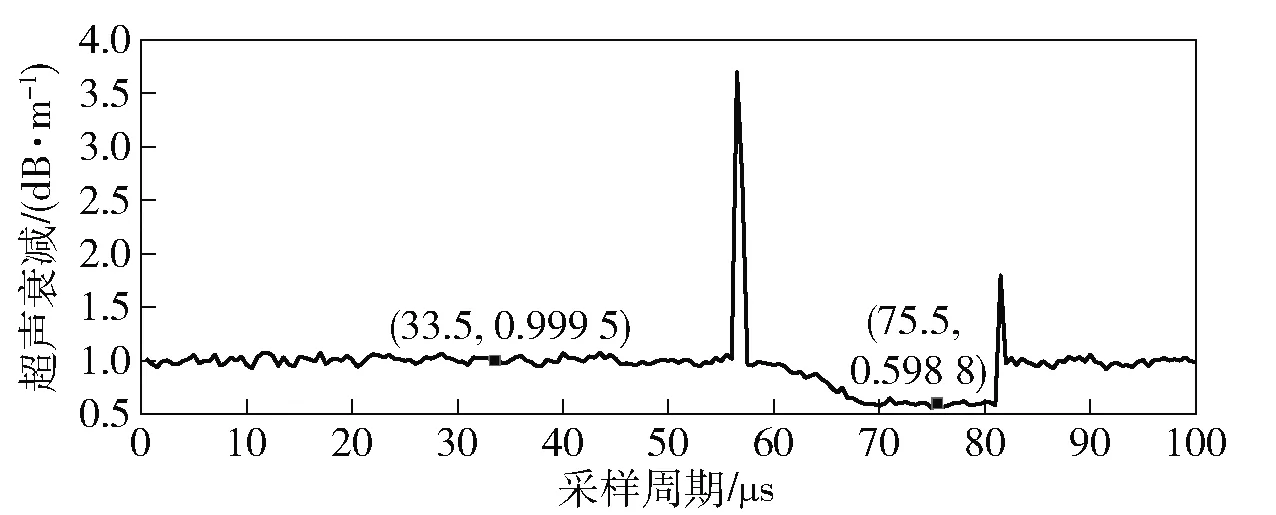
图4 超声信号在浓度场中的回波衰减

同时避免信号的偶然性，共进行了3次火箭撬穿越3个浓度不同的云雾箱试验，3次试验的超声衰减结果如表6所示。

4.3 对比分析

对仿真分析结果和试验测试数据进行结果对比，超声衰减与仿真的浓度值具有一致性，如图5所示。在设定的标称浓度分别为75 g/m3、150 g/m3、225 g/m3的引信-云雾交会条件下，由表5不同标称浓度对应的仿真浓度和由表6仿真浓度对应的超声最大衰减结果可知：1号箱体标称浓度为75 g/m3，子引信动态仿真浓度为72.5 g/m3，超声衰减率为11.87%；2号箱体标称浓度为150 g/m3，子引信的动态仿真浓度为130 g/m3，超声衰减率为23.22%；3号箱体标称浓度为225 g/m3，子引信动态仿真浓度为220 g/m3，超声衰减率为44.31%.对比显示，二者具有一致性，验证了超声衰减用于燃料云团浓度探测的可行性。

表6 仿真浓度与超声信号相对衰减多次测试结果

图5 仿真浓度与超声衰减的对应关系

5 结论

本文对云雾场高高速超声衰减浓度检测引信样机进行了流体力学仿真和试验验证，在以100 m/s的高速运动下穿过3个浓度分别为75 g/m3、150 g/m3、225 g/m3的云雾箱后，得到仿真浓度和超声回波衰减曲线。得出主要结论如下：

1)引信样机与环境短暂交会时间窗口内，样机内流道云雾浓度形成稳定流形，并获得了稳定状态下的最大浓度数值。

2)通过比较多个环境浓度下的最大浓度值和超声衰减率，发现了二者的一致性，初步验证利用超声在云雾中传播衰减进行浓度探测的可行性。

参考文献(References)

[1] 张博，白春华.气相爆轰动力学[M].北京:科学出版社，2013.

ZHANG B，BAI C H.Dynamics of gas phase detonation[M].Beijing:Science Press，2013.(in Chinese)

[2] 张宝钅平，张庆明，黄凤雷.爆轰物理学[M].北京：兵器工业出版社，2001.

ZHANG B P，ZHANG Q M，HUANG F L.Detonation physics[M].Beijing: Publishing House of Ordnance Industry，2001.(in Chinese)

[3] 郭明儒.云爆燃料浓度快速多模检测机理与方法研究[D].北京：北京理工大学，2016.

GUO M R.Study on the mechanism and method of rapid multimode detection of cloud explosion fuel concentration[D].Beijing:Beijing Institute of Technology，2016.(in Chinese)

[4] YAMAZAKI H，TOJO K，MIYANAMI K.Concentration profiles of solids suspended in a stirred tank[J].Powder Technology，1986，48(3):205-216.

[5] OMOTAYO K，PAUL R A，MICHAEL J P，et al.Cashdollar effectiveness of dust dispersion in the 20-L Siwek chamber[J].Journal of Loss Prevention in the Process Industries，2010，23(1): 46-59.

[6] LLOYD P.Wave propagation through an assembly of spheres: II.The density of single-particle eigenstates[J].Proceedings of the Physical Society，1967，90(1):207.

[7] RIEBEL U.Characterization of agglomerates and porous particles by ultrasonic spectrometry[C]∥Proceedings of the 5th European Symposium on Particle Characterization.Nürnberg，Germany:the European Federation of Chemical Engineering, 1992.

[8] 乔榛.超声法一次风流速和煤粉浓度在线测量研究[D].南京：南京理工大学，2013.

QIAO Z.Research on on-line measurement of primary air velocity and pulverized coal concentration of primary air using ultrasonic method[D].Nanjing: Nanjing University of Science and Technology，2013.(in Chinese)

[9] 郭盼盼，苏明旭，陈丽，等.蒙特卡罗方法预测液固两相体系中颗粒的超声衰减[J].过程工程学报，2014，14(4):562-567.

GUO P P，SU M X，CHEN L，et al.Prediction of ultrasonic attenuation in liquid-solid particulate two-phase system Monte Carlo method[J].The Chinese Journal of Process Engineering，2014，14(4): 562-567.(in Chinese)

[10] 郭明儒，娄文忠，金鑫，等.燃料空气炸药固体燃料浓度动态分布试验研究[J].兵工学报，2016，37(2):226-231.

GUO M R，LOU W Z，JIN X，et al.Experimental research on dynamic concentration distribution of fae solid fuel[J].Acta Armamentarii，2016，37(2):226-231.(in Chinese)

[11] FU S H，LOU W Z，WANG H J，et al.Evaluating the effects of aluminum dust concentration on explosions in a 20 L spherical vessel using ultrasonic sensors[J].Powder Technology，2020，367(1):809-819.

[12] FU S H，LOU W Z，LI C B，et al.Concentration dynamic probe of micro/nano aluminum powder[C]∥Proceedings of the 19th 2019 IEEE International Conference on Nanotechnology.Macau，China:IEEE，2019:425-428.

[13] 付胜华，娄文忠，李楚宝，等.云爆子引信-云团高速交会浓度探测[J].兵工学报，2021，42(5):897-902.

FU S H，LOU W Z，LI C B，et al.On concentration detection of fae cloud at high-speed intersection between fae cloud and sub-fuze[J].Acta Armamentarii，2021，42(5):897-902.(in Chinese)

[14] 马银亮.高浓度气固两相流的数值模拟研究[D].杭州：浙江大学，2001.

MA Y L.Numerical simulation of high concentration gas-solid two-phase flow[D].Hangzhou: Zhejiang University，2001.(in Chinese)

[15] 袁竹林，耿凡，彭正标，等.气固两相流动与数值模拟[M].南京：东南大学出版社，2013：10-11.

YUAN Z L，GENG F，PENG Z B，et al.Gas-solid two-phase flow and numerical simulation[M].Nanjing:Southeast University Press，2013：10-11.(in Chinese)

[16] 张鸣凤，章易程，张方圆，等.吹吸式地铁轨间区域清扫流场的数值分析[J].哈尔滨工业大学学报，2020，52(9):137-143.

ZHANG M F，ZHANG Y C，ZHANG F Y，et al.Numerical analysis on blowing-suction cleaning flow field between subway rails[J].Journal of Harbin Institute of Technology，2020，52(9):137-143.(in Chinese)

[17] 封文轩，杨道业.基于融合传感器的气固两相流参数检测系统设计[J].仪表技术与传感器，2020(3):95-99.

FENG W X，YANG D Y.Design of gas-solid two-phase flow parameter detection system based on fusion sensor[J].Instrument Technology and Sensor，2020(3):95-99.(in Chinese)