空间绳系组合体的继电型控制离轨策略
郭甲,庞兆君,岳帅,杜忠华
南京理工大学 机械工程学院,南京 210094
在人类掌握太空发射技术后,各个国家已经向太空中发射了数以万计的航天器,这些航天器在失效后成为空间碎片。这些空间碎片若与正常工作的航天器发生碰撞,将对航天器安全和宇航员的生命产生致命威胁[1]。为清理空间碎片,各国提出了相应的空间碎片主动清除计划,其中“捕获+离轨”式清除方案被普遍接受[2-3]。近些年来,空间系绳捕获系统是“捕获+离轨”式方案近些年来研究的热点。空间系绳捕获系统一般由太空拖船、系绳、末端捕获装置构成。末端捕获装置捕获到目标后,太空拖船与目标由系绳连接,组成绳系组合体。之后太空拖船进行机动,拖曳目标至坟墓轨道完成空间碎片清除任务[4]。
国内外学者针对拖曳离轨过程中的主要问题进行了大量的研究。在离轨策略方面,钟睿和徐世杰[5]利用直接配置算法研究了绳系组合体的霍曼转移方法,Liu等[6]在霍曼转移使用两次脉冲推力机动的基础上,研究了利用重力梯度辅助完成拖曳离轨的可能性,并给出了具体的实施方式。但是使用脉冲转移方法对于系绳较短的绳系组合体并不适用,因为轨道根数在短时间内发生大尺度的变化会导致系绳的剧烈振动。Liang等[7]提出了使用小推力离轨的方法并建立了失效卫星的转移动力学方程。李超兵等[8]针对脉冲式推力研究了一种基于轨道根数约束的空间变轨最优制导方法。Cho和Mcclamroch[9]最早提出了绳系组合体的最优轨道转移方法,以径向推力和横向推力的平方和最小化为目标,设计了2个圆形轨道间的转移路径。文献[10-11]研究了一种基于连续常值推力的时间-能量最优的离轨方式,并考虑了绳系组合体轨道机动过程中控制量饱和对系统稳定的影响。杨乐平等[12]总结称,推力模式除了脉冲推力、连续推力外,常见的还有继电型推力模式,但目前在绳系组合体领域对继电型推力模式的研究并不多。
在离轨过程中,太空拖船的推力并不总是沿着系绳方向,并会导致系绳的摆动。刘海涛[13]指出,当太空拖船与目标径向方向速度有差值时,绳系组合体会剧烈摆动,导致任务失败。文献[14-15]研究了离轨过程中系绳摆动特性与其他物理量的耦合关系。文献[16-17]将绳系组合体的面内摆动处理为欠驱动系统,并利用以系绳张力作为控制输入的滑模控制器来使摆动趋于稳定。王秉亨等[18]研究了张力受限条件下的高阶滑模控制器以实现绳系组合体的稳定。王班等[19]对无系绳收放控制的绳系组合体横向摆动与纵向振动的耦合进行了分析,并提出了一种双闭环振动控制策略。刘新建和郑杰匀[20]研究了无卷扬机构时,使用脉冲喷气抑制绳系组合体摆动的可能性。黄静等[21]针对电动力绳设计了在展开阶段抑制系绳摆动的控制策略。上述文献表明为了降低拖曳离轨的风险,离轨策略的设计需要考虑对系绳摆角的抑制。
连续推力在绳系组合体拖曳的理论研究中得到了广泛应用,但实际中需要考虑更多限制因素。其中连续变推力设计复杂,工程实现困难。连续常值推力多通过电推进发动机实现,但因推力过小,导致其实现离轨目标需要漫长的时间。工程实际中更多使用继电式推力,因其符合脉冲调宽式推力器的工作方式,且可实现与连续推力近似的效果[22]。
为了使拖曳离轨功能更加方便地在工程中实现,本文提出一种绳系组合体的继电型推力拖曳离轨策略。首先,为了解决发动机开机对系绳造成冲击与关机时系绳反弹的问题,设计一种无需电机驱动的卷扬机构。由于此卷扬机构是被动式的,无法主动调整系绳张力来抑制面内摆角,所以利用太空拖船的径向推力来抑制面内摆角,考虑到实际中径向推力发动机能够提供的推力有限,设计输入受限的滑模控制器生成控制指令,之后再将其转化为继电式推力,以便于工程实现。
1 绳系组合体动力学分析
1.1 绳系组合体离轨动力学模型
为了描述拖船与目标之间的相对运动,需要引入2个坐标系:
1)惯性坐标系OE-XYZ:即地心赤道惯性坐标系,其原点在地心,X轴指向春分点;Z轴垂直于赤道面指向北极;Y轴由右手定则确定。
2)组合体质心轨道系O-xyz:其原点位于系统质心O,x轴由地心指向组合体质心;y轴在轨道平面内与x轴垂直,沿运动方向为正;z轴垂直于轨道平面,与x、y构成右手系。
将坐标系O-xyz绕轴顺时针旋转γ角,再绕轴逆时针旋转φ角,y轴将与太空拖船和目标的连线方向重合。将γ记为面内摆角,φ记为面外摆角(图1)。为了便于描述,将太空拖船编号c,目标编号b,作为参数的下标使用。
记rc、rb分别是太空拖船和目标的绝对位置矢量,在惯性坐标系OE-XYX中,二者的轨道动力学方程分别为
(1)
(2)
式中:μ为地球引力常数;Fc为太空拖船发动机提供的控制力矢量;T为系绳上的张力矢量,方向由目标指向太空拖船;mc为太空拖船质量;mb为目标质量。
太空拖船与目标之间的相对位置矢量记为de=rb-rc,则联立式(1)、式(2)可以得到
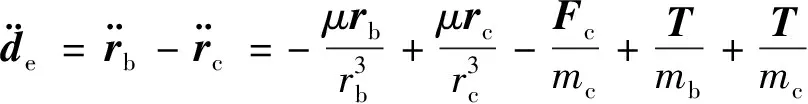
(3)
式(3)为太空拖船与目标相对运动动力学方程在惯性系OE-XYZ中的表达式。为得到精确相对运动方程,将其转换到坐标系O-xyz中,则可以得到非线性相对运动动力学模型的矢量形式:

(4)
式中:ω为绳系组合体的轨道角速度矢量。
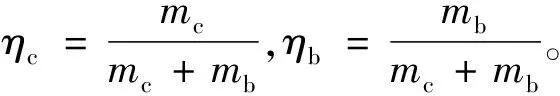
d=[x,y,z]T
(5)
(6)
(7)
(8)
Fc=[Fx,Fy,Fz]T
(9)
T=[Tx,Ty,Tz]T
(10)
rc=[r-ηbx,-ηby,-ηbz]T
(11)
rb=[r+ηcx,ηcy,ηcz]T
(12)
将式(5)~式(12)代入式(4),可得
(13)

(14)
式中:a为轨道长半轴;e为偏心率;i为轨道倾角;Ω为升交点赤经;Ψ为近地点幅角;θ为真近点角。改进春分点轨道根数动力学方程如下:
(15)


(16)
1.2 系绳张力求解
不同于现有的利用电机收放系绳来控制张力的主动式卷扬机构,设计如图2所示被动式卷扬机构,系绳的张力由此卷扬机构确定。当太空拖船与目标之间的距离增加,系绳被拉出,储线筒正转,通过储线筒齿轮及涡卷发条盒齿轮带动涡卷发条盒正转,放置在涡卷发条盒内部的涡卷发条被上紧。当太空拖船与目标之间的距离减小,涡卷发条被释放并带动涡卷发条盒反转,进而带动储线筒反转,系绳被回收。通过系绳被拉出与被回收的过程,系绳上的张力得以保持,而张力的大小与涡卷发条的特性以及储线筒齿轮与涡卷发条盒齿轮的传动比有关。因为系绳自身的弹性模量远远大于涡卷发条,因此,可忽略离轨过程中系绳自身的变形。涡卷发条会对太空拖船产生反作用力,但其产生的扭矩较小,可利用太空拖船上的动量轮进行抵消。

图2 被动式卷扬机构
根据机械设计手册[23],涡卷发条的工作特性如图3所示。涡卷发条放入发条盒并完全放松时的圈数用ns表示。曲线CIJ表示涡卷发条输出力矩与发条弹簧圈数(发条盒转数)的关系。曲线CI段(其转数用n0表示)力矩变化大,不能利用。直线BN是发条的理论力矩曲线。当发条外端固定方式为衬片固定时,输出力矩为理论力矩的90%~95%。由于二者差距较小,因此使用理论力矩曲线对扭矩与圈数的关系进行简化,此时涡卷发条输出的扭矩M与被上紧的圈数n成正比,二者关系可以表示为

图3 涡卷发条工作特性[23]
M=β1n+M0
(17)
式中:M0为涡卷发条预紧扭矩;β1为一大于0的常数,由涡卷发条材料及加工工艺确定。
涡卷发条输出的扭矩经过齿轮传动传递到储线筒上,且涡卷发条输出的扭矩与储线筒上的扭矩大小比值为z2/z1,其中z1为储线筒齿轮齿数,z2为涡卷发条盒齿轮齿数。储线筒上的扭矩除以储线筒的半径R为系绳上的张力。由此可以推出系绳上张力T与被上紧的圈数n的关系为
(18)
为了减小拖船与目标碰撞的可能性,当系绳被完全回收时,拖船与目标间需留有安全距离ds,即拖船与目标距离d为被拉出系绳长度L与安全距离ds之和。由此可以计算得到d与涡卷发条被上紧的圈数n的关系为
(19)
进而可以推出系绳张力与拖船与目标之间距离d的关系式为
(20)
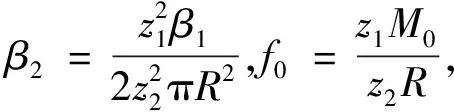
T=β2(d-ds)+f0d>ds
(21)
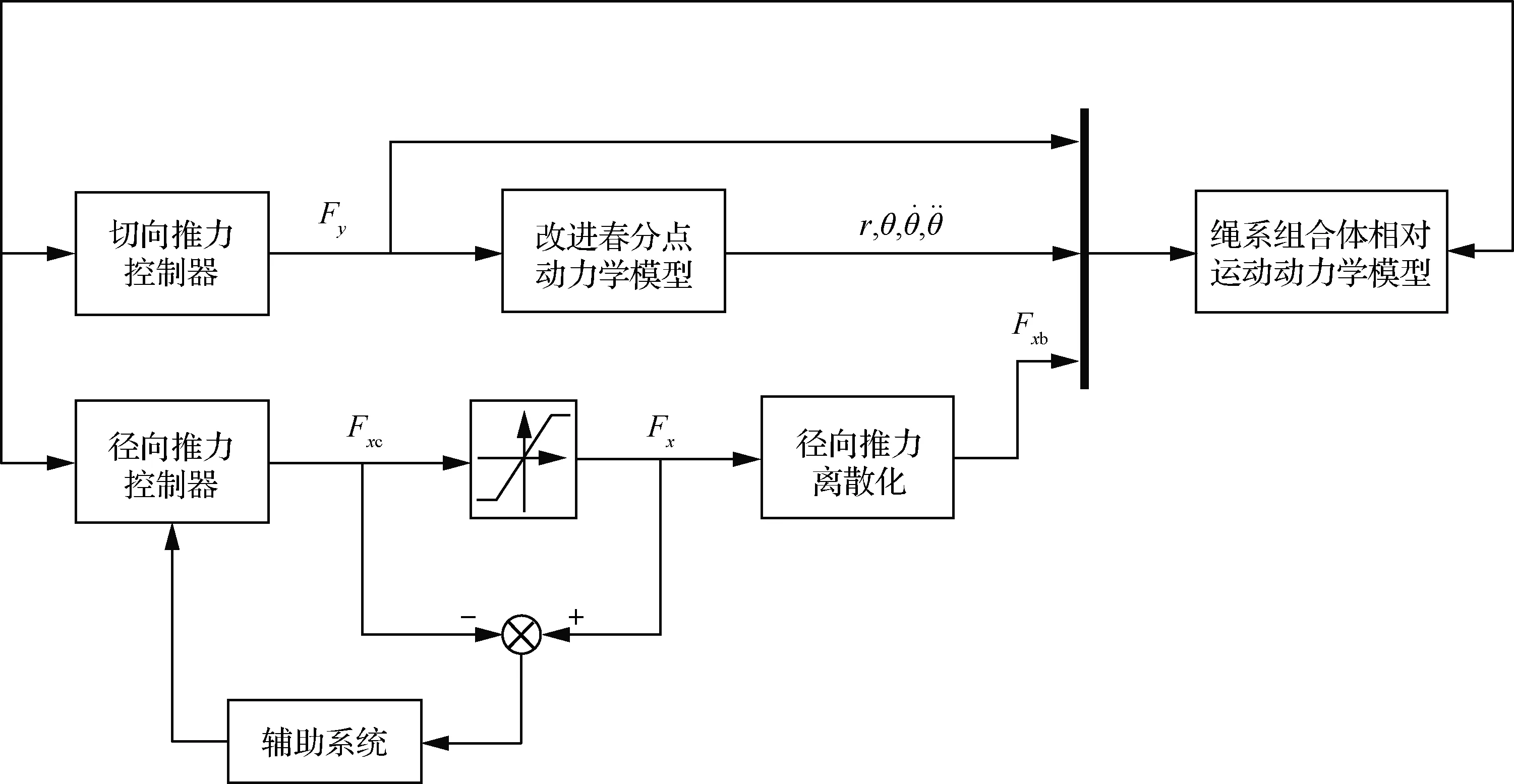
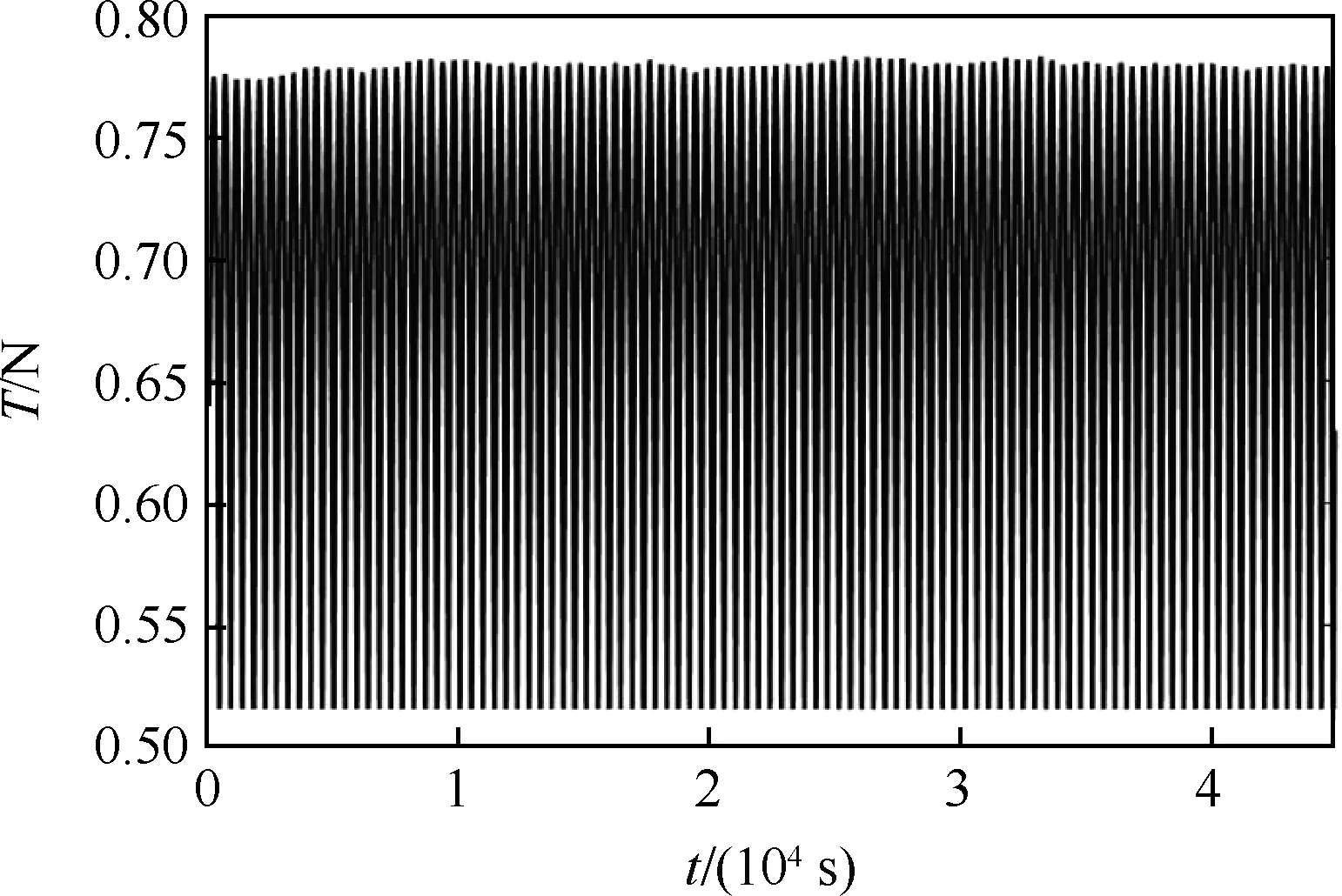
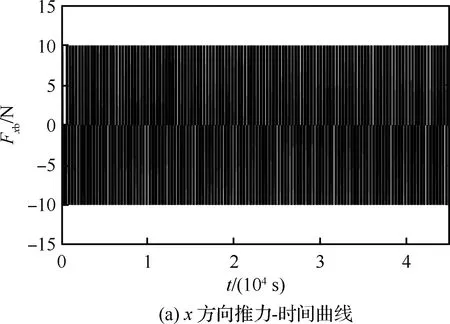
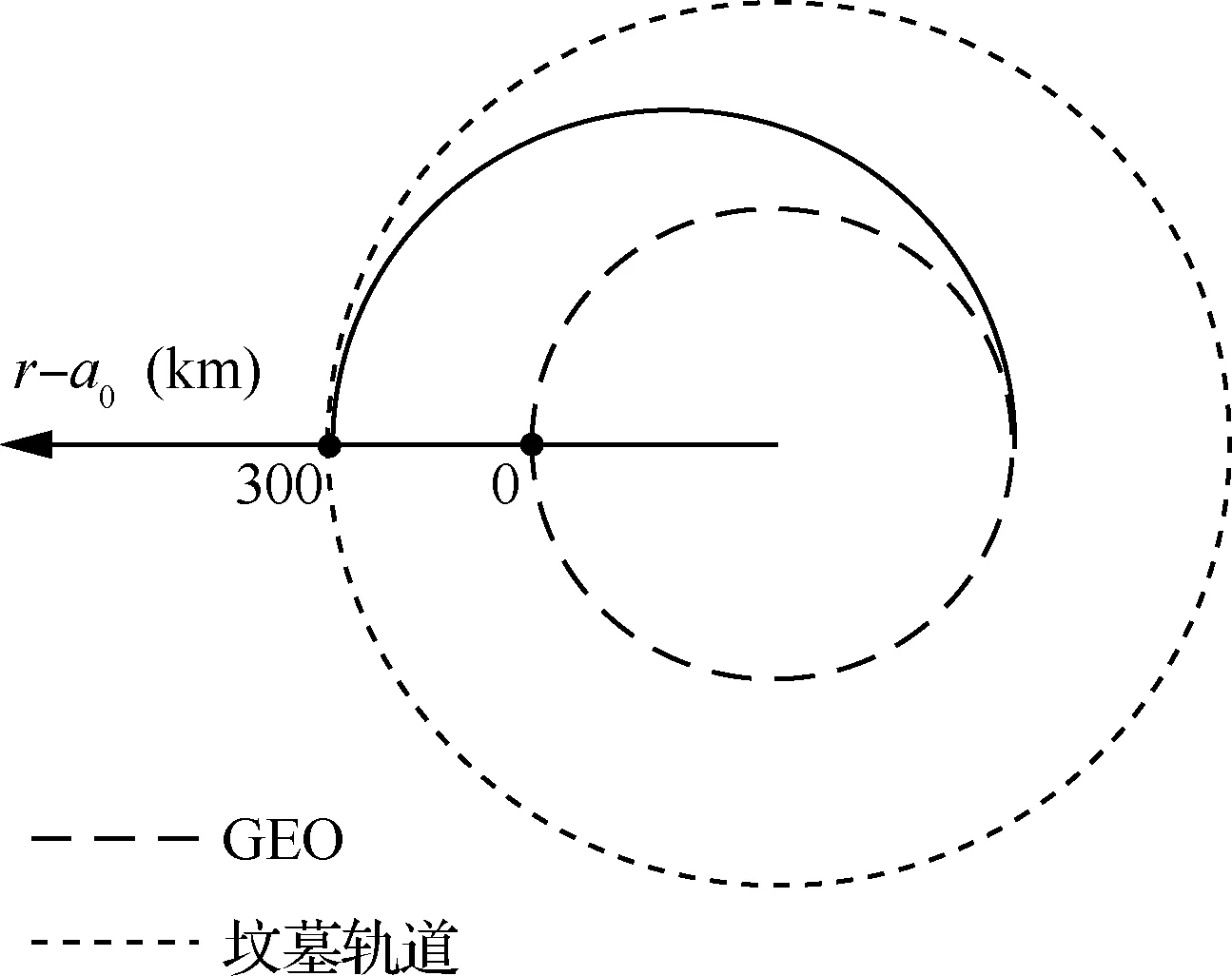
当d T=0d (22) 太空拖船的发动机提供的切向推力对应动力学模型中的Fy,其采取继电式推力模式,其推力大小恒定,每次开机时间长短可调,如图4所示。 图4 继电式推力模式 图5 切向推力轨迹 设切向推力发动机状态为u(t),当u(t)=1时,切向推力发动机开机;当u(t)=0时,切向推力发动机关机。为实现上述带差动间隙的Bang-Bang 控制策略,需要发动机在不同情况下的状态为 (23) 需要注意的是当发动机关机停止作用后,飞行器与目标之间距离不会立即减小。太空拖船在系绳张力的作用下开始减速,目标在系绳张力作用下继续加速,但因发动机关机时太空拖船速度大于目标速度,故太空拖船需要减速一段时间后速度才会小于目标速度。在这段时间内,二者之间距离仍是增加的,系绳需空出一段安全长度作为这段时间的缓冲。同理,当发动机开启后,二者距离不会立即增加,而是继续经过一段时间的距离减小后才开始增加,所以也需要一段系绳作为缓冲。 绳系组合体离轨过程中,期望面内摆角为0 rad。根据文献[11],初始摆动速度不为0 rad/s时,实际离轨过程中面内摆角会在0 rad附近波动。若摆动速度达到一定值,绳系组合体将不再稳定。为了维持绳系组合体的稳定,需要对面内摆角进行抑制。因为被动式卷扬机构无法主动调整张力来抑制面内摆角,所以利用径向推力进行面内摆角的抑制。现实中径向的推力发动机能够提供的推力有限,因此在设计控制器时必须要考虑“控制输入饱和”的问题,否则会使得整个控制系统不稳定[24]。本文首先利用控制输入受限的滑模控制器生成连续变推力形式的控制指令,再将其转化为继电式推力指令以便于工程实现。 记Ix为组合体质心轨道系O-xyz中x轴的基矢量,d′=[x,y,0]T为d在O-xyz坐标系xOy平面内的投影,二者大小分别记和d′、Ix,则面内摆角计算公式为 (24) (25) 式(25)相较于式(13)多出的Fd项为考虑到实际径向发动机推力存在误差添加的扰动项,有|Fd|≤D。控制输入为Fx,控制目标为q1→qd,q2→0。 径向推力受发动机功率的限制,设Fxc为受限前的控制量,Fx为受限后的控制量,径向推力的最大值为Fxmax,ΔFx=Fx-Fxc,Fx与Fxc的关系为 (26) 利用一个稳定的自适应辅助系统,可以实现控制输入饱和的补偿,设计辅助系统为 (27) 式中:λ1、λ2为补偿项。为了保证t→∞时,λ1,λ2→0,需要k1>0,k2>0。 定义方向的误差为 δ=q1-qd-λ1 (28) 则有 (29) 设滑模函数为 (30) 式中:k为大于0的常数。将式(25)~式(30)联立可得 (31) (32) 设计控制器为 k1(-k1λ1+λ2)+k2λ2-ξsgn(s)] (33) (34) 定义Lyapunov函数: (35) 则有 (36) 图6 推力转化方式 孟云鹤和戴金海[22]通过理论推导得出结论:当N足够大时,上述2种推力模型相对位置控制作用的偏差为一阶小量,而相对速度偏差至少是一阶小量,说明在适当划分“控制小区间”的情况下,2种推力模型的控制作用在一阶意义上等效,彼此之间可以相互转换。 至此绳系组合体的控制策略完成,包括离轨控制策略与面内摆角抑制控制策略。整个拖曳离轨策略控制律如图7所示。 图7 绳系组合体离轨控制策略 绳系组合体初始轨道为地球静止轨道(Geostationary Orbit, GEO),根据计算可得到改进春分点轨道根数如表1所示。 表1 改进春分点轨道根数初值 假设拖船与目标之间的安全距离ds设为38 m。因涡卷发条需要预紧,预紧圈数对应绳长为2 m,可得拖船与目标之间的初始距离为40 m,则二者的初始相对坐标为d=[0 m,-40 m,0 m]T。文献[11]提到初始时刻太空拖船与目标 设计卷扬机构时,期望系绳上的张力取值范围为[0.5 N,1 N]。同时期望系绳被完全拉出时太空拖船与目标之间的距离不要超过100 m,所以设置卷绕在线筒上的系绳长度为50 m。由此可以确定系绳每被拉出1 m,系绳上的张力增加0.01 N,系绳上张力的表达式为 (37) 太空拖船径向可提供的推力大小为±10 N,故控制输入受限的滑模控制器中Fxmax=10 N。设k1=10,k2=10,k=0.031,ξ=0.001,λ1、λ2初值为0。径向的扰动力为 Fd=0.5sint (38) 将滑模控制器生成的连续变推力转换为继电式推力时,时间区间的长度Δt为10 s。 径向推力的控制指令经历了2次转化才最终成为绳系组合体的真实输入。第1次变化由控制输入受限导致,如图8(a)所示,前10 s内限制前控制力Fxc超过10 N,则限制后控制输入Fx为10 N,之后二者重合。 第2次变化是将受限后的连续推力Fx转化为继电式推力Fxb,如图8(b)所示。受限连续推力初始大小为10 N,随着时间增加,面内摆角波动变小,控制力也趋向于0。继电式推力在[-10 N,0 N,10 N]3种状态中切换,连续推力在10 s区间内产生的冲量越多,继电式推力在10 s区间内作用的时间越长。 图8 径向推力前100 s变化曲线 图9显示了整个拖曳离轨过程中面内摆角在无控制、受限连续推力、继电式推力3种情况下的变化情况;图10则显示了在离轨过程前2 000 s内面内摆角的变化。 从图9可以看出,在无控制条件下,绳系组合体面内摆角在-1.5~1.5 rad范围内变化,现实中绳系组合体将会发生剧烈摆动。在施加控制力的条件下,可以将面内摆角抑制在0 rad左右。 图9 离轨全过程面内摆角变化曲线 图10显示了绳系组合体从初始状态到稳定状态需要大概400 s的时间。400 s以后,结合图9可以发现若使用受限连续推力,面内摆角能够维持在0 rad。若使用继电型推力,面内摆角在400 s之后会在一定范围内波动,但波动的范围非常小,为-0.02~0.02 rad。 图10 前2 000 s面内摆角变化曲线 图11为拖船与目标之间距离的变化情况,图12为拖曳过程中系绳张力的变化。因为被动式卷扬机构中的涡卷发条提供的扭矩与转动圈数成正比,而系绳张力与扭矩成正比,距离与转动圈数成正比,所以系绳上的张力正比于拖船与目标间的距离,二者变化图形相似,如图13所示。整个离轨过程中系绳张力的变化范围为0.5~0.8 N,期间张力连续不突变,避免了发动机开关机对系绳的冲击。同时张力不大于1 N,可以确保系绳不会断裂。由于切向方向的继电式推力以及被动式卷扬机构的特性,拖船与目标间的距离会发生大范围的、近似周期性的变化,变化范围为39~67 m。二者距离一直大于38 m,满足离轨过程中拖船与目标保持安全距离的要求。 图11 拖船与目标间距离的变化 图12 系绳张力变化曲线 图13 前2 000 s距离与系绳张力的关系 图14(a)、图14(b)分别为绳系组合体在整个离轨过程中拖船推力变化情况。二者皆为继电式推力,x方向的推力Fxb在[-10 N,0 N,10 N]范围内切换,y方向的推力则仅有[0 N,50 N]两种状态。受面内摆角变化影响,Fxb与Fy在前400 s变化更加频繁,图形更加密集。图14(c)显示面内摆角稳定后,Fy呈现出类似周期性的变化,一个周期约为490 s,每个周期内开机时间约为10 s。 图14 离轨过程的拖船推力变化 图15为离轨全过程内视图。整个离轨过程耗时约12 h,离轨过程中绳系组合体的远地点,轨道半径,半长轴相较于GEO轨道半径a0都在逐渐增加。经历约半个椭圆的飞行过程后,近地点提升了300 km,轨道半径,远地点,半长轴的提升则大于300 km,轨道的偏心率变为0.004 9。 图15 离轨全过程内视图 为了方便空间绳系捕获系统清理空间碎片任务的工程实现,提出一种继电型推力离轨策略,其中离轨目标与面内摆角抑制皆通过继电型推力实现。同时为了解决继电式推力给组合体带来冲击的问题,设计了一种不同以往的被动式卷扬机构。 通过仿真分析可以得到以下结论: 1)基于继电式推力机动的卫星拖曳离轨策略能够满足绳系组合体的离轨要求。在整个离轨过程中,系绳上的张力一直大于0且保持在一个较小的范围内,避免了系绳打结或断裂的危险。同时,系绳张力连续,不会发生突变,避免了发动机开机对系绳的冲击以及关机时系绳回弹带来的风险。 2)在太空拖船与目标径向方向具有一定速度差值的初始状况下,若不对面内摆角进行控制,绳系组合体将会剧烈摆动。在无法主动调整系绳张力且径向推力有限的情况下,通过输入受限的滑模控制器控制太空拖船的径向推力可以有效抑制绳系组合体的面内摆角。当绳系组合体径向受到扰动时,滑模控制器也表现出了较好的鲁棒性,消除了扰动力对面内摆角的影响。 3)将抑制面内摆角的连续推力转化为继电型推力后,仍可以实现面内摆角的抑制,但相较于连续推力效果存在细微差距。使用连续推力可以使面内摆角保持在0 rad,使用继电型推力面内摆角则会有±0.02 rad的微小波动。但继电式推力在工程实际中更容易实现,相较于连续推力有其自身的优势。2 绳系组合体控制策略
2.1 绳系组合体离轨控制策略




2.2 面内摆角抑制控制策略
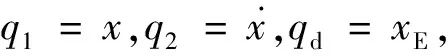

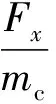

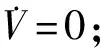


3 数值仿真校验
3.1 仿真条件设置

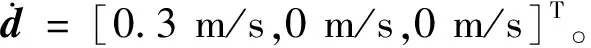
3.2 仿真分析





4 结 论

