一类变系数波方程耦合系统解的爆破

兰 杰

(山西财贸职业技术学院，山西 太原 030031)

0 引言

研究此变系数波方程耦合系统:

(1)

其中Ω⊂Rn(n≥2)是具有光滑边界∂Ω的有界区域，a,b>0,p>1,q>2是常数.A(x)=(aij(x))为正定的对称矩阵，aij(x)是Rn中的光滑函数.

变系数波方程耦合系统，在文献[1-4]中都进行了深入的讨论.文献[1]用Sobolev嵌入定理讨论了一类波方程的解的情况，文献[2]讨论了系统(1)局部解的适定性；文献[3]说明了在pq时，系统(1)[2-4]解的爆破情况.

1 预备知识

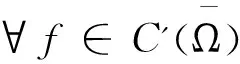
∇gf=A(x)∇f

其中∇f为f在Euclidean空间下的梯度.

对系统(1)[2]作出如下假设：

(A1)存在θ>0使得

(A2)p>q,且满足：

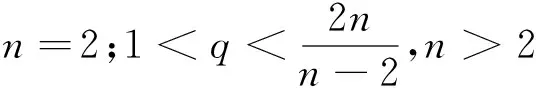
定义能量泛函[2]如下：

其中

2 主要结论的证明

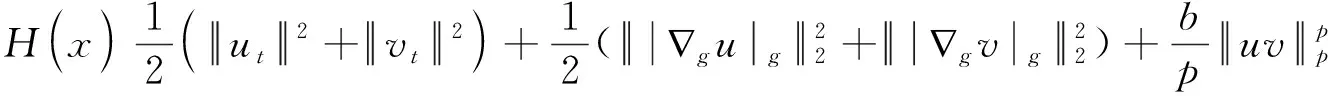
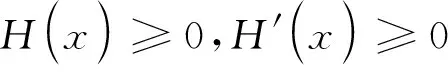
(2)

则：

因为

(3)

根据Young’s不等式

(4)

(5)

(6)

因为

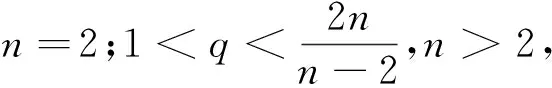
由Sobolev嵌入定理[1]

(7)

可得：

则

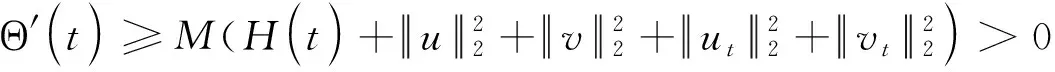
(8)

由Young’s不等式，Sobolev嵌入定理[1]，Hölder’s不等式得：

(9)

则结合(8)、(9)，一定存在ζ，使得