考虑时空紧迫度的船舶碰撞动态风险估计方法*
刘 钊 陈 阳 张明阳
(1.武汉理工大学航运学院 武汉 430063;2.武汉理工大学内河航运技术湖北省重点实验室 武汉 430063;3.武汉理工大学国家水运安全工程技术研究中心 武汉 430063;4.阿尔托大学工程学院机械工程系 芬兰 艾斯堡 20110)
0 引 言
船舶碰撞事故是最常见的水上交通事故之一,其带来的后果不仅会造成船舶、货物等财产损失,而且可能造成人命损失或者燃油泄漏等,严重威胁人命财产和水域环境安全[1-2]。为减少船舶碰撞事故发生率,提高船舶航行安全和交通效率,船舶碰撞风险评价已成为水上交通安全领域的研究热点。
近年来,国内外学者对船舶碰撞风险评价进行了研究并取得了众多成果。Zhen等[3]根据最小会遇距 离(distance at the closest point of approach,DCPA)和最小会遇时间(time to the closest point of approach,TCPA)利用负指数函数构建船舶碰撞风险函数,提出了1种用于海上交通监视的实时船舶碰撞风险评价模型;Chen等[4]采用基于速度障碍的船舶碰撞风险评价方法,从速度的角度对船舶碰撞风险进行评价;江行等[5]将船舶领域、海上避碰规则与碰撞危险度模糊评价模型相结合,提出了基于四元船舶领域和避碰规则的碰撞危险度模型。但目前的船舶碰撞风险评价方法大多基于DCPA和TCPA指标[6],该方法主要用于开阔水域中的船舶碰撞风险评价,对于繁忙受限水域中的船舶碰撞风险评价,其危险程度与实际情况不符[7]。
为了解决繁忙受限水域中的船舶碰撞风险评价问题,部分学者利用船舶领域[8]对船舶碰撞风险进行评价。Qu等[9]根据模糊船舶领域的重叠次数来评价新加坡海峡的船舶碰撞风险;Wang[10-11]在四元船舶领域的基础上,引入了纵向风险和横向风险的概念来估计船舶的空间碰撞风险;张照亿等[12]选取KIJIMA船舶领域模型来界定船舶安全会遇范围,结合其几何形状,提出了基于船舶领域模型的船舶碰撞风险评价方法。但是,船舶领域在船舶碰撞风险评价中的应用主要根据他船进入本船领域的方位和距离判定,仅考虑了船舶碰撞的空间要素[13],忽略了船舶碰撞的时间要素。
因此,针对船舶碰撞风险评价方法在繁忙受限水域中的局限性,在空间上基于船舶领域应用二维平面空间接近程度,在时间上考虑船舶的瞬时接近程度,建立考虑时空紧迫度的碰撞风险计算模型,以期得到适用于繁忙受限水域的船舶碰撞动态风险计算方法,为船舶的安全监管和避碰决策提供支持。
1 研究方法
1.1 研究思路
船舶碰撞风险是由船舶之间的时空距离决定的,主要包括空间指标和时间指标2个指标要素。首先,根据船舶的长度,应用藤井船舶领域模型[14-15]确定会遇船舶的船舶领域,并对船舶领域进行分层处理,结合船舶领域每层的赋值,计算船舶领域叠加区域的数值计算值;同时,根据船舶的瞬时相对方位,计算同方位船舶发生碰撞时的叠加区域数值计算值,进而采用船舶领域叠加区域的数值计算值与同方位船舶发生碰撞时的叠加区域数值计算值的比值作为船舶碰撞空间紧迫度的表征函数;然后,根据船舶的位置与速度,确定会遇船舶的相对位置和相对速度,计算相对速度在相对位置上的投影,通过船舶之间距离除以相对速度在相对位置上的投影得到船舶碰撞时间,进而对碰撞时间进行标准化处理得到0~1之间的船舶碰撞时间紧迫度的表征函数;最后,运用突变理论建立船舶碰撞风险计算模型。船舶碰撞风险计算建模流程见图1。
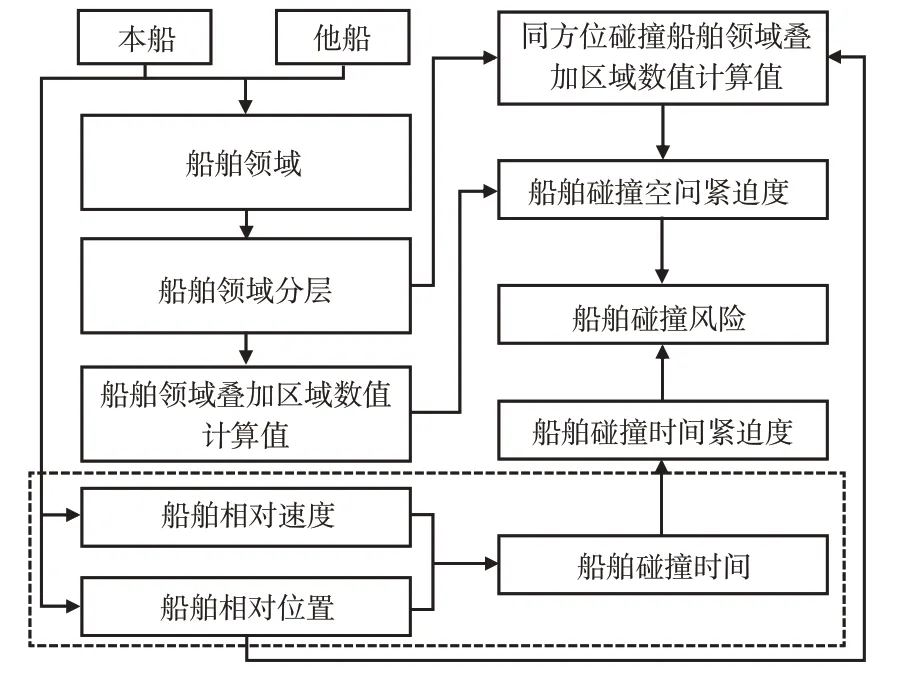
图1 船舶碰撞风险计算建模流程Fig.1 Modelingprocessonthecalculationofvesselcollisionrisk
1.2 船舶碰撞空间紧迫度
目前,评价船舶碰撞风险的空间指标多采用DCPA或者船舶间的距离,考虑的是船舶之间的直线距离上的风险。运用船舶领域理论将船舶碰撞风险的空间指标拓展为二维平面空间,综合考虑船舶周围他船的分布规律与距离接近带给驾引人员的心理压力,在藤井船舶领域模型的基础上将船舶领域内部层级按照指数函数进行层级划分并分别赋值,作为船舶碰撞空间紧迫度计算的基础。
1)船舶领域分层。将船舶等效成长轴为船长、短轴为船宽的椭圆,将船舶边界与领域之间的区域由内而外均分为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ层,对于船长为L、船宽为B的船舶,其船舶领域分层见图2,分层尺度见表1。
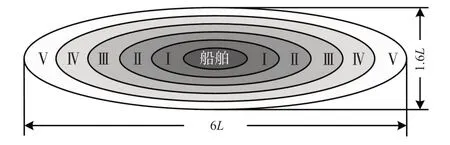
图2 船舶领域分层示意图Fig.2 Classic ship domain model
2)船舶领域层级赋值。将船舶领域层级按照以2为底的指数函数进行权重赋值,见表1。

表1 船舶领域层级边界尺度及权重赋值Tab.1 Boundary scale and weight assignment of vessel level domain
3)船舶层级数值。根据船舶领域分层与船舶内部层级权重赋值,用交叉相加的方法来标定25种船舶领域叠加层权重,见表2。

表2 船舶领域叠加层级权重赋值Tab.2 Weight assignment on overlap of vessel level domain
根据2船船舶领域分层叠加面积以及各叠加层的权重赋值,2船船舶领域分层加权的叠加面积的数值计算见式(1)。
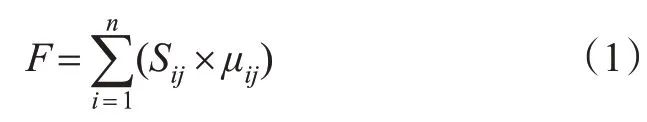
式中:F为2船船舶领域叠加面积数值计算值;Sij为1船舶第i层与另1船舶第j层的叠加区域面积值;μij为不同层级叠加权重(取值参照表2)。
4)船舶碰撞空间紧迫度函数。运用船舶同方位发生碰撞时的2船船舶领域叠加面积数值计算值对船舶碰撞空间进行标准化处理,建立船舶碰撞空间紧迫度函数见式(2)。

式中:Kt为t时刻船舶碰撞空间紧迫度,范围0~1;Ft为t时刻2船船舶领域叠加面积数值计算值;Ft-max为t时刻同方位2船碰撞发生时的船舶领域叠加面积数值计算值。
1.3 船舶碰撞时间紧迫度
目前,评价船舶碰撞风险的时间指标多采用TCPA,体现的是船舶到达最小会遇点的时间,由于船舶航向、航速等行为的动态性,最小会遇点的位置也具有不确定性,致使TCPA在风险分析中难以达到理想的效果。运用船舶的相对速度和相对位置,求取船舶的瞬时相对接近速度,再结合船舶的瞬时相对距离,得到船舶该情景下的碰撞时间,作为船舶碰撞时间紧迫度的基础。
1)船舶相对位置。通过船舶AIS(GPS位置信息)可获得准确的位置、速度和相对方位信息。将t时刻船舶A的位置信息表示为(xAt,yAt)、船舶B的位置信息表示为(xBt,yBt),则t时刻船舶A到船舶B的相对位置矢量见式(3)。
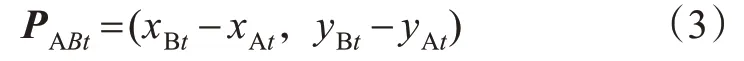
2)船舶相对速度。根据船舶的航速和航向数据,可将船舶速度进行矢量化处理。将t时刻船舶A的速度表示为vAt、航向表示为αAt,船舶B的速度表示为vBt、航向表示为αBt,则t时刻船舶A到船舶B的相对速度矢量见式(4)。
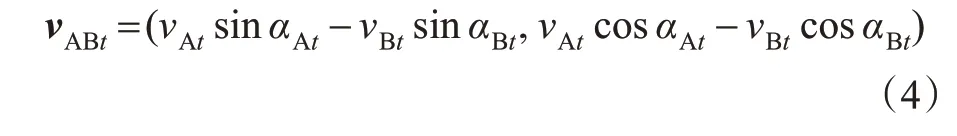
3)船舶碰撞时间。船舶碰撞时间是指在t时刻相对位置和相对接近速度的条件下,从t时刻到船舶发生碰撞时的时间差,根据船舶的相对位置矢量和相对速度矢量求取船舶碰撞时间的方法见式(5)。
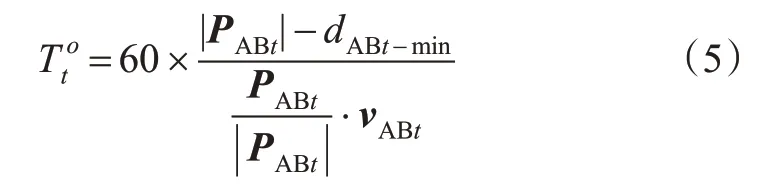
式中:Tto为船舶碰撞时间,即在t时刻相对位置和相对接近速度的条件下,从t时刻到船舶发生碰撞时的时间差,min;PABt为t时刻船舶A到船舶B的相对位置矢量;|PABt|为t时刻船舶之间的距离(nmile,1nmile=1 852 m);vABt为t时刻船舶A到船舶B的相对速度矢量,km;dABt-min为t时刻船舶A到船舶B发生碰撞时的最小距离,n mile。
4)船舶碰撞时间紧迫度函数。根据船舶碰撞时间与碰撞风险之间的关系,运用指数函数建立船舶碰撞时间紧迫度函数见式(6)。
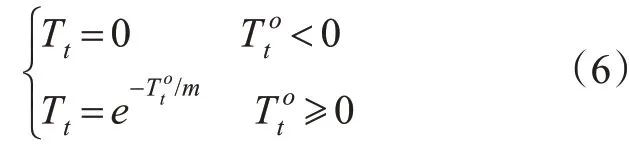
式中:Tt为t时刻船舶碰撞时间紧迫度,范围0~1;为船舶碰撞时间,min;m为大于0的调节系数,可根据专家咨询或大数据统计拟合得到。
1.4 突变理论
突变理论是法国数学家Thom在1972年创立的,是以奇点理论、微分方程稳定性理论、拓朴学、群论和分叉理论等数学理论为基础,用来研究和解决跃迁和不连续现象的数学理论[16-17]。突变理论在使用过程中,把研究的问题看作1个系统,该系统在演化过程中,某些变量的连续变化最终会导致系统状态的突然变化,即从1种稳定的状态跃到另1种稳定的状态。
突变理论是通过势函数来研究系统突然的现象,即系统可以通过系统的势函数V=f(U,X)来表达,其中U={u1,u2,…,un}是系统的外部控制参量,X={x1,x2,…,xm}是系统状态变量[18]。在各种可能变化的外部控制参量和内部行为变量的集合条件下,构造状态空间和控制空间。通过联立求解V′(x)和V"(x),得到系统平衡状态的临界点,突变理论正是通过研究临界点之间的相互转换来研究系统的突变特征。
尖点突变是1种初等突变,其势函数为状态空间即二轴,是一维的,控制空间为二维平面。尖点突变的势函数见式(7),突变流形见式(8),归一化公式见式(9)。
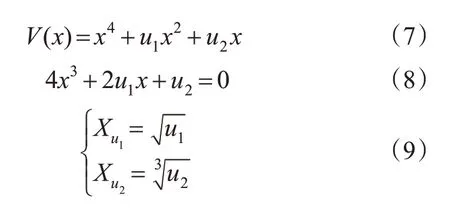
式中:x为状态变量;u1,u2为控制变量。
采用突变理论对系统进行评价的步骤包括确定评价指标、建立评价模型和评价系统状态等3个步骤。其中,建立评价模型需要考虑指标之间的相互关系,对于符合非互补准则的指标,1个系统的诸控制变量之间,其作用不可互相替代,即不可相互弥补其不足,按“大中取小”原则取值;对于符合互补准则的指标,诸控制变量之间可相互弥补其不足,按其均值取用;对于符合过阈互补准则的指标,诸控制变量必须达到某一阈值后才能互补。使用尖点突变理论建立系统评价模型,首先对状态变量和控制变量的取值进行归一化处理,使其取值范围均处于0~1的范围;然后根据控制变量之间的重要程度与指标之间的关系,基于尖点突变理论的归一化公式建立符合互补准则的系统状态评价函数见式(10)。

式中:R为系统状态值;u1,u2为控制变量,其重要程度为u1>u2。
2 船舶碰撞动态风险计算方法
2.1 2船碰撞风险计算模型
船舶碰撞空间紧迫度与时间紧迫度是船舶碰撞风险评价的核心指标。空间紧迫度和时间紧迫度可相互弥补其在时空范围上对船舶碰撞风险反映的不足,是互补性指标;并且空间紧迫度的重要性大于时间紧迫度。根据船舶碰撞空间紧迫度和时间紧迫度的函数,基于突变理论建立2船船舶碰撞风险计算模型见式(11)。

式中:Rt为t时刻船舶碰撞风险值;Kt为t时刻船舶碰撞空间紧迫度,范围0~1;Tt为t时刻船舶碰撞时间紧迫度,范围0~1。
根据2船船舶碰撞动态风险计算模型,会遇2船的碰撞风险总是相同,船舶风险表征值取值范围为0~1,船舶距离较远时风险值较小,船舶发生碰撞时风险值为1,船舶碰撞风险随时空紧迫度的增加呈非线性变化。
2.2 多船船舶碰撞风险计算模型
多船会遇是船舶航行中常见的情景,因此多船会遇碰撞风险计算是评估船舶航行安全面临的重要问题之一。传统DCPA和TCPA风险判断法仅能够辅助驾驶员对单一他船的碰撞风险做出度量,在多船会遇时的风险判断则完全依靠驾驶员经验来完成,然而不同驾驶员对风险的理解往往不同,可能过大或者过小地定义自身风险,无形中增加船舶安全航行的负担。建立多船舶碰撞风险度量模型有助于解决上述问题。
在2船船舶碰撞动态风险计算模型的基础上构建多船会遇情景下的任一船舶碰撞风险计算模型需要考虑的原则有:①对任一船舶,船舶碰撞风险最大值为1,即任一船舶与他船发生碰撞,则该船舶的碰撞风险为1,其他船舶对该船舶的风险应不再予以叠加;②对任一船舶,若未与他船发生碰撞,则该船舶的碰撞风险应小于1,且大于该船舶与单个任意他船碰撞风险的最大值;③任一船舶的碰撞风险不应小于0。根据上述原则,建立多船船舶碰撞风险计算模型见式(12)。
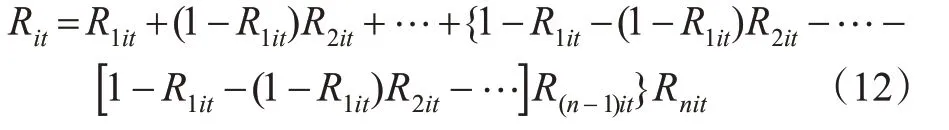
式中:Rit为船i在t时刻与他船的总碰撞动态风险值;R1it,R2it,…,Rnit分别为t时刻不同他船对船i构成的碰撞风险,且R1it≥R2it≥…≥Rnit;n为会遇船舶数量。
3 模型验证
3.1 实验场景设置
为了验证船舶碰撞动态风险计算模型的有效性,运用Python进行模拟仿真实验。实验场景设置为多船会遇场景,其中船A与船B为追越局面,船A与船C为对遇局面,船A与船D为交叉相遇局面。船A初始位置坐标点为(0,0),船A航向为X轴正方向,左正横为Y轴正方向,船A与其他船舶之间的相对位置关系见图3。实验船舶的长度、宽度、航速、航向、船首向及他船与船A的初始相对方位、距离见表3。
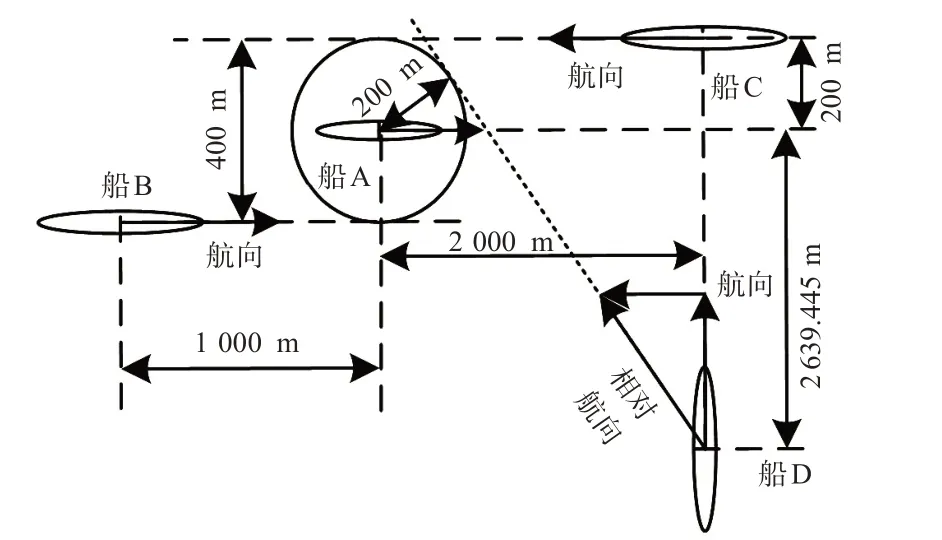
图3 船舶相对位置示意图Fig.3 Relative positions of vessels

表3 实验船舶数据表Tab.3 Experimental data of vessels
3.2 船舶碰撞动态风险计算结果
运用Python进行仿真得到船A与船B,C,D的2船碰撞动态风险变化曲线见图4。
由图4可知:船A与船B的非零碰撞空间紧迫度存在时间最长,碰撞动态风险最值最小;船A与船C的非零碰撞空间紧迫度存在时间最短,碰撞时间紧迫度最值最大;船A与船D的碰撞空间紧迫度及碰撞动态风险的最值最大。反映了船舶在不同会遇局面中的碰撞风险特征,符合船舶碰撞威胁的实际情况。此外,船A与船B、船C的碰撞空间紧迫度最值相同,这是由船A到达船B、船C正横方向时的距离相等造成的。
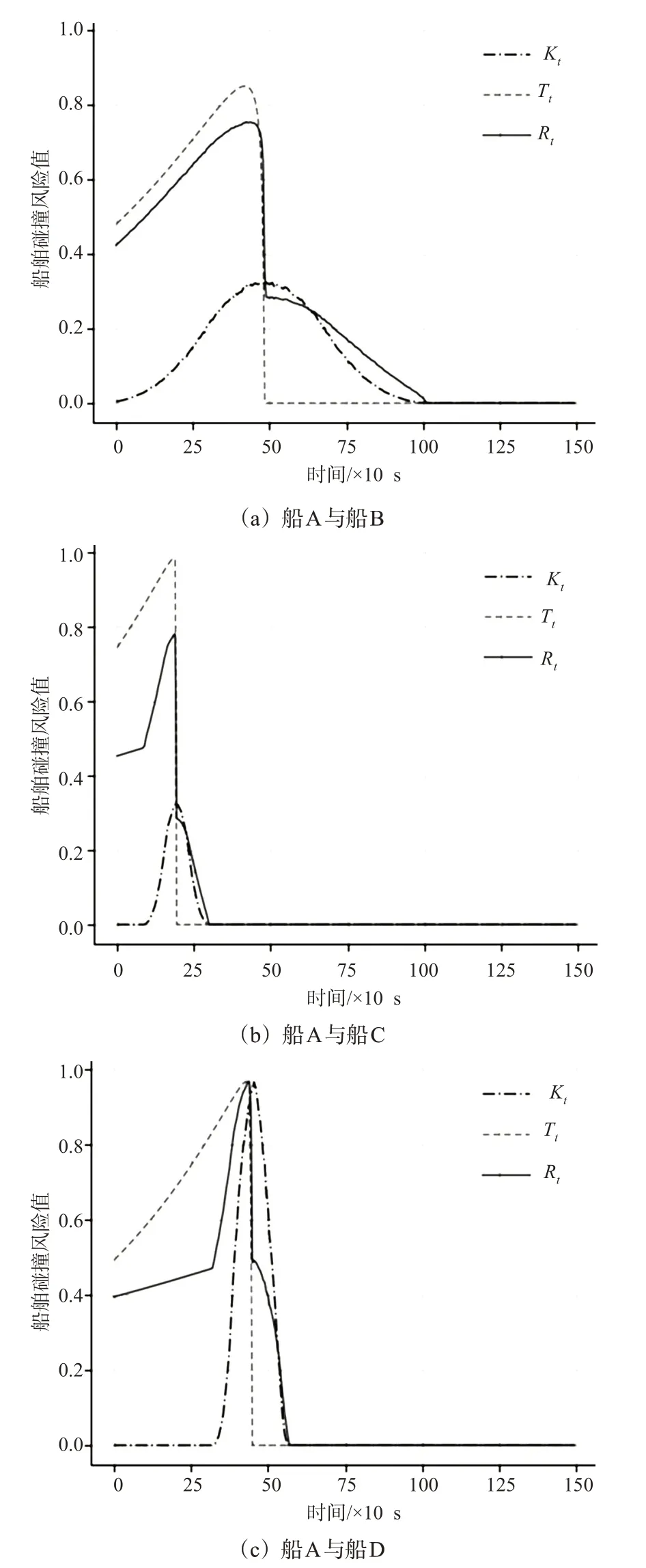
图4 船A与船B,C,D的2船碰撞风险Fig.4 Collision risk among vesselAand vessels B,C,and D
依据船A与船B,C,D的2船碰撞动态风险值,则船A与其他3艘船舶的多船碰撞动态风险变化曲线见图5。
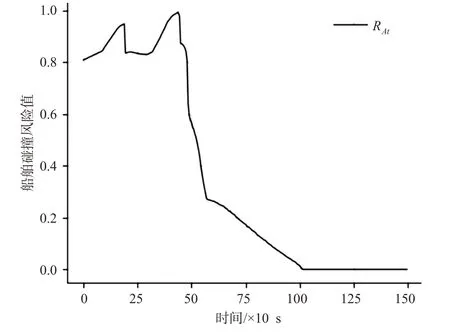
图5 船A与船B,C,D的多船碰撞风险Fig.5 Multi-vessel collision risk among vesselAand vessels B,C,and D
由图5可知:船A与船B,C,D的多船碰撞动态风险存在2个峰值,分别为0.949(190 s)和0.992(440 s)。第1个峰值受船A与船C的碰撞风险影响最大,第2个峰值受船A与船D的碰撞风险影响最大。
3.3 结果分析
为了验证本文提出的船舶碰撞风险计算模型,利用DCPA和TCPA及基于时空距离的碰撞风险评估模型[19]进行比较。不同方法得出的船A与船B,C,D的碰撞风险及计算结果对比见图6和表4。
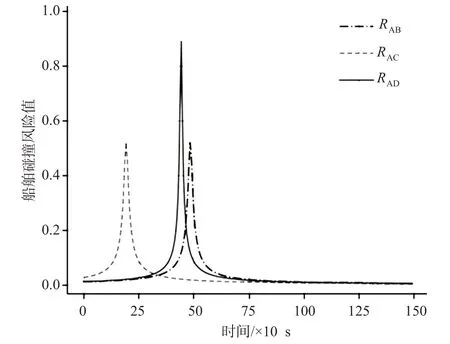
图6 船A与船B,C,D的基于时空距离的碰撞风险Fig.6 Spatio-temporal distance-based collision risk among vesselAand vessels B,C,and D
由表4和图4~6可知,使用本文提出的船舶碰撞动态风险模型得到船A与船B,C,D的碰撞风险客观反映了当时的交通风险等级。且与TCPA方法对比,本文提出模型具有提前警示船舶采取避让行为的特征。综合考虑船舶会遇接近过程中受水动力的干扰和船舶驾驶人员对碰撞风险的认知,本文提出方法更符合船舶碰撞风险预警的实际情况,可促进船舶提前采取避让行为以降低避碰风险。
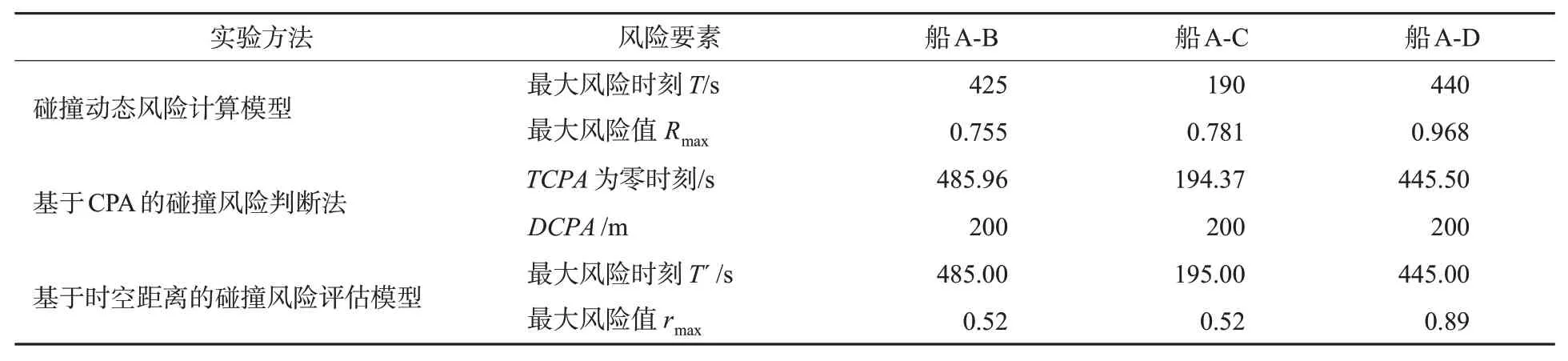
表4 3种风险计算方法结果对比Tab.4 Comparison of the results of three risk-calculation methods
此外,在会遇船舶DCPA相同的时候,由于船舶最小会遇点位置的不同,船舶碰撞风险会存在较大的差异。因此,船舶碰撞风险的变化具有非线性特征,然而基于时空距离的碰撞风险评估模型难以实现碰撞风险的非线性表征。例如,设置船A与船B,C,D的DCPA都为200 m,利用时空距离的碰撞风险评估模型评估碰撞风险,表明基于时空距离的碰撞风险评估模型计算得到的结果存在跳变现象。其评估结果难以为船舶驾驶员提供避碰决策理论支持。
对以上2种典型碰撞风险模型进行对比分析,结果表明本文提出的船舶动态风险模型克服了DCPA和TCPA及基于时空距离的碰撞风险评估方法对船舶碰撞风险预警的滞后性和非线性变化表征不足的问题。证明了本文方法具有一定的有效性和实用性,可为船舶避碰决策系统的开发提供理论基础。
4 结束语
本文提出了1种考虑时空紧迫度的船舶碰撞风险计算方法。该方法考虑了船舶长度、宽度、航速、航向和船首向等要素,利用船舶领域叠加区域数值,构建了船舶碰撞空间紧迫度计算模型,实现了船舶碰撞动态风险计算。并利用仿真实验与对比分析,验证了所提出模型的有效性和实用性。具体结论总结如下。
1)本文提出船舶碰撞动态风险计算方法将船舶碰撞的空间要素由线(距离)拓展到了面(船舶领域叠加区域),克服了DCPA和TCPA及基于时空距离的船舶碰撞风险评估方法对风险非线性变化表征不足的问题。
2)考虑时空紧迫度的船舶碰撞风险计算模型实现了碰撞风险的风险性表征,结果能够更准确地、及早刻画船舶碰撞风险,符合船舶碰撞威胁的实际情况,可为船舶避碰决策提供参考。
今后,可利用船舶AIS大数据,考虑船舶操作环境,进一步优化船舶领域模型,实现真实场景下的船舶碰撞风险可接受阈值的量化,为船舶的智能避让决策系统开发奠定理论基础。

