低能见度水平下行人交通事故严重程度及异质性分析*

董傲然 秦 丹 王长帅 朱秭硕 朱 彤▲

（1.长安大学运输工程学院 西安 710064；2.东南大学交通学院 南京 210096）

0 引 言

道路交通伤害已经成为全球人员死亡的第八大原因，道路交通安全问题依然是全球性的公共健康问题[1]。根据世界卫生组织（WHO）发布的2018年《全球道路交通安全现状报告》显示，全球每年有135万人死于道路交通事故。中国人口众多，交通事故频发，2018年中国共发生244 937起交通事故，造成63 194人死亡，直接经济损失达13.8亿元，中国的道路交通安全形势也相当严峻[2]。在交通事故中，行人作为弱势道路使用者，由于缺少外部的保护，其在事故中更容易遭受严重伤害[3]。根据美国国家公路安全管理局发布的《Traffic Safety Facts》[4]，2007—2016年，虽然交通事故死亡总数从41 259下降到了37 461，但是行人死亡人数却从4 699上升到了5 987，行人死亡率从11%上升到了16%。此外，WHO发布的2013年《世界健康报告》[5]显示，行人伤亡人数占道路交通事故伤亡总人数的22%，而在中国，这一占比更是达到了25%。虽然各国已经采取许多措施来降低事故中行人的伤害，但是交通事故中的行人伤害问题仍不可忽视。

国内外学者针对行人事故伤害严重程度已经开展了大量的研究，Aziz等[6]利用随机参数logit模型分析了纽约市行人伤害严重程度，发现道路、交通，以及土地利用特征是影响行人伤害严重程度的主要因素；Haleem等[7]运用混合Logit模型分析了在有信号控制和无信号控制交叉口与行人伤害严重程度有关的因素。在影响行人-机动车交通事故严重程度的因素中，能见度水平是1项重要因素，低能见度情况下视野范围变小，机动车较难发现行人，遇到紧急情况时留给驾驶员或行人的反应时间大幅减少，容易发生行人伤害事故[8]。因此，能见度对于道路交通参与者的安全有重要影响，有必要对低能见度机动车-行人事故严重程度进行研究。

离散选择模型是常用的事故数据分析模型。王涛等[9]采用有序Logit模型对影响电动自行车事故严重程度的因素进行分析和讨论；Rezapour等[10]运用有序Logit模型对单车和多车事故进行研究，发现影响单车和多车事故严重程度的因素存在显著差异。但传统Logit模型属于固定参数模型，其认为影响因素在不同事故严重程度的作用是不变的，但交通事故是由多类复杂因素共同作用的事件，获取与交通事故相关的所有信息是非常困难的，往往会缺失必要的事故信息，从而导致分析时会产生有偏差的参数估计，这被称作未观测到的异质性，而传统Logit模型无法识别数据中未观测到异质性。

针对事故数据中的异质性，许多学者运用随机参数模型进行分析。Kim等[11]运用混合Logit模型分析了北卡罗来纳州的机动车-行人碰撞事故；Wu等[12]运用混合Logit模型对新墨西哥州的农村双车道道路上的单车和多车碰撞事故分别进行了研究；陈昭明等[13]构建了混合Logit模型，准确识别影响高速公路交通事故严重程度的因素，并提出了刻画参数间相关性的方法。随机参数模型主要聚焦于识别伤害严重程度函数中的随机参数，但随机参数中可能存在个体异质性，若忽略个体异质性则可能会导致有偏差的参数估计值[14]。2016年，Mannering等[15]引入1种允许将随机参数的均值或方差与模型中的变量相关联以识别个体异质性的方法，并运用到了对高速公路事故的分析之中，为异质性模型的研究奠定了基础。此后，Seraneeprakarn等[16]运用考虑均值异质性和均值-方差异质性的随机参数Logit模型研究涉及混合动力车辆的事故严重程度，并证明了此模型要优于传统的随机参数Logit模型。

综上，国内外学者在行人事故研究方面已取得一定成果，但国内外的交通情况与事故致因存在一定差异，低能见度情况下的事故伤害严重程度研究依然缺乏，且传统模型无法识别数据中的异质性。因此运用考虑均值异质性的随机参数Logit模型对我国的低能见度下机动车-行人事故进行分析，探究影响低能见度事故中行人伤害严重程度的因素，识别可能未观察到的异质性，为相关部门制定行人保护对策提供一定的理论支持。

1 数据描述

从某市交通管理部门获得了2006—2017年行人-机动车碰撞事故数据。数据详细记录了如驾驶员和行人特征、车辆特征、道路特征和环境因素等事故信息。在剔除了不完整和明显有误的记录后，筛选出6 405例事故数据进行分析。

本研究的因变量为机动车-行人碰撞事故中行人的受伤严重程度，可分为4类：无伤害、轻伤、重伤、死亡。在本研究中，由于行人无伤害事故数据较少，故将无伤害事故和轻伤事故合并为1组。根据每个类别的数据量、碰撞属性和驾驶员伤害严重性属性的相似性，将行人伤害严重程度进一步分为3组：无伤害或轻伤、重伤、死亡，其中，无伤害或轻伤作为基准变量。

根据《水平能见度等级》[17]和事故数据特征，将能见度水平划分为200 m及以下为低能见度情况，200 m以上为高能见度情况。在3 347起低能见度事故中，1 882份报告为无伤害或轻伤，占车祸车辆总数的56.23%，439份（13.12%）报告为重伤，1 026份（30.65%）报告为死亡；在3 058起高能见度事故中，2 037份报告为无伤害或轻伤，占车祸车辆总数的66.61%，454份（14.85%）报告为重伤，567份（48.54%）报告为死亡。可以看出，与高能见度事故中的行人相比，低能见度事故中的行人死亡的风险更高。表1为变量的描述性统计。

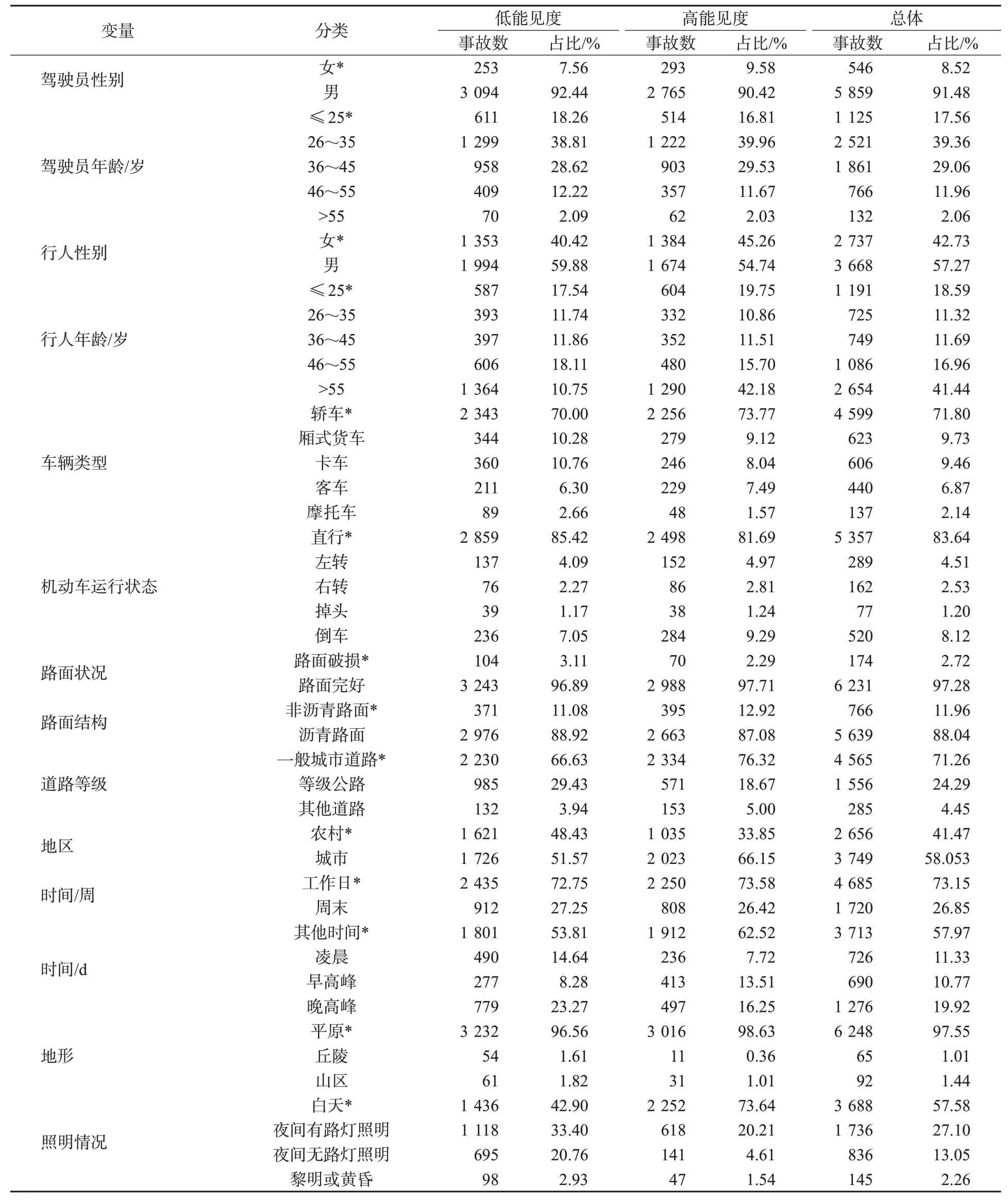
表1 变量的描述性统计Tab.1 Descriptive statistics of variables

2 模型构建

2.1 均值异质性的随机参数Logit模型

选用考虑均值异质性的随机参数logit模型识别影响事故中行人伤害严重程度的因素，效用函数为

式中：Sin为决定事故n中的行人伤害严重程度为i的效用函数；Xin为影响事故中行人n的严重程度因素的向量；βi为对应的估计参数的向量；εin为误差项。

为了解释可能未观测到的异质性，定义βn为随事故n而变化的估计参数的向量集，βn的表达式见式（2）[18]。

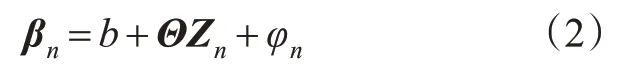
式中：b为事故中的平均参数估计值；Zn为事故n中均值异质性向量，它会影响βn的均值；Θ为对应的估计参数的向量；φn为随机分布的误差项，用以捕捉事故中未观察到的异质性。

在存在未观测到的异质性的情况下，使得β具有1个连续的密度函数f(β|φ)，则事故伤害严重程度概率密度函数可表达为

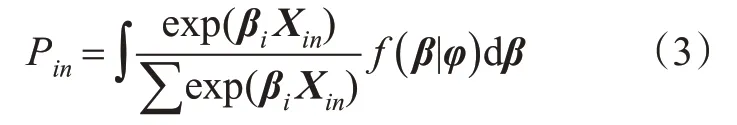
式中：f(β|φ)为β的概率密度函数；φ为描述密度函数的参数向量。

通过基于仿真的最大似然估计方法对式（3）中的参数进行估计，采用Halton抽样方法，抽样次数为200次。在进行估计之前，必须指定参数的概率密度函数的形式。参数的概率密度函数的函数形式通常为正态分布、对数正态分布、三角分布和均匀分布。以往的文献得出的普遍结论是，正态分布通常最适合事故伤害严重程度数据[19]。

2.2 弹性分析

利用均值异质性的随机参数Logit模型得出的回归参数只能定性地反映显著自变量对事故中驾驶人受伤严重程度的影响趋势，并不能定量地反映显著自变量对机动车间事故中驾驶人受伤严重程度的影响大小。为了评估均值异质性的随机参数Logit模型中的显著变量对驾驶员伤害结果概率的影响，还需进行弹性分析。弹性分析计算见式（4）。

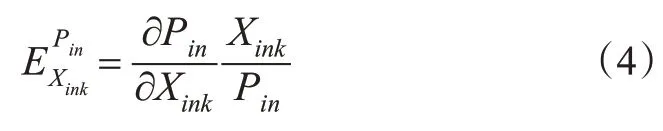
然而式（4）适用于连续变量，不适用于指标变量（值为0或1的变量），因为概率对于值0或1的变量不可微。为了解决这个问题，可以计算1个伪弹性来量化指标变量的边际效应，见式（5）。

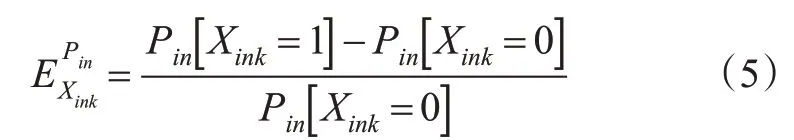
3 结果讨论

低能见度情况下的事故中行人伤害严重程度的估计结果见表2，根据似然比检验的结果，考虑均值异质性的随机参数logit模型的对数似然初始值为-3 188.411 3，对数似然收敛值分别为-2 755.085 9，AIC值为5 602.2，McFadden PseudoR2为0.250 7，表明模型整体的拟合优度良好。高能见度情况下所有变量的回归参数的标准差均在统计意义上不显著，所有参数均退化为固定参数，因此模型退化为多项式Logit模型。根据似然比检验的结果，高能见度情况下的多项式Logit模型的AIC值为4 792.7，对数似然初始值为-2 649.050 8，对数似然收敛值为-2 367.348 6，多项式Logit模型拟合良好。

3.1 随机参数

根据表2，在低能见度的情况下，有2个变量具有服从正态分布的随机参数特征，分别为对应伤害严重程度为死亡的类别中的变量“卡车”和“凌晨”。如图1（a）所示，变量“卡车”服从均值为1.643，标准差为1.773的正态分布，这意味着在低能见度的情况下，事故中82.3%的行人在涉及卡车的事故受到致命伤害的可能性会增加，而17.7%的行人在涉及卡车事故中受到致命伤害的概率则会降低。变量“凌晨”对于伤害严重程度为死亡的类别服从均值为0.867，标准差为1.469的正态分布（见图1（b）），这意味着在低能见度的情况下，相对于其他时间，有72.2%的行人在凌晨发生的事故中受到致命伤害的概率增加，而27.8%的行人在凌晨发生的事故中受到致命伤害的概率会有所降低。

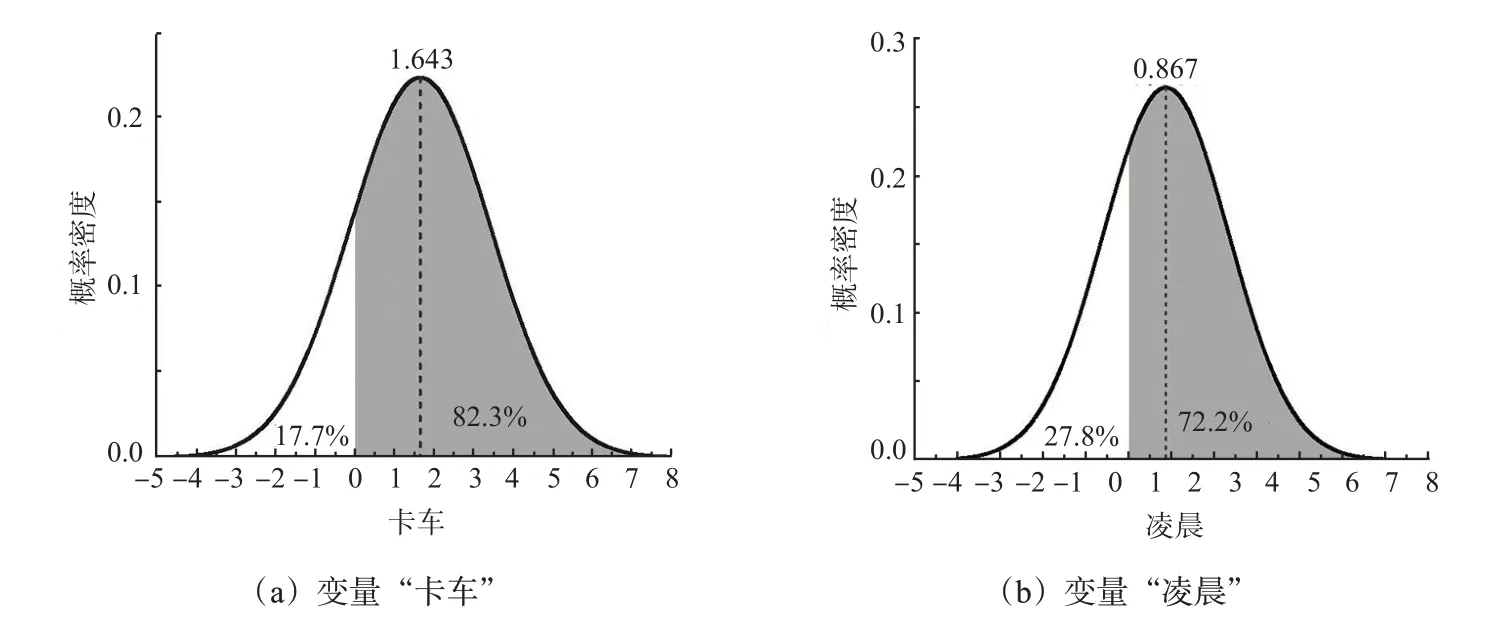
图1 随机参数分布Fig.1 Distribution of random parameters

根据表2，高能见度情况下的显著变量不具有随机参数特征。

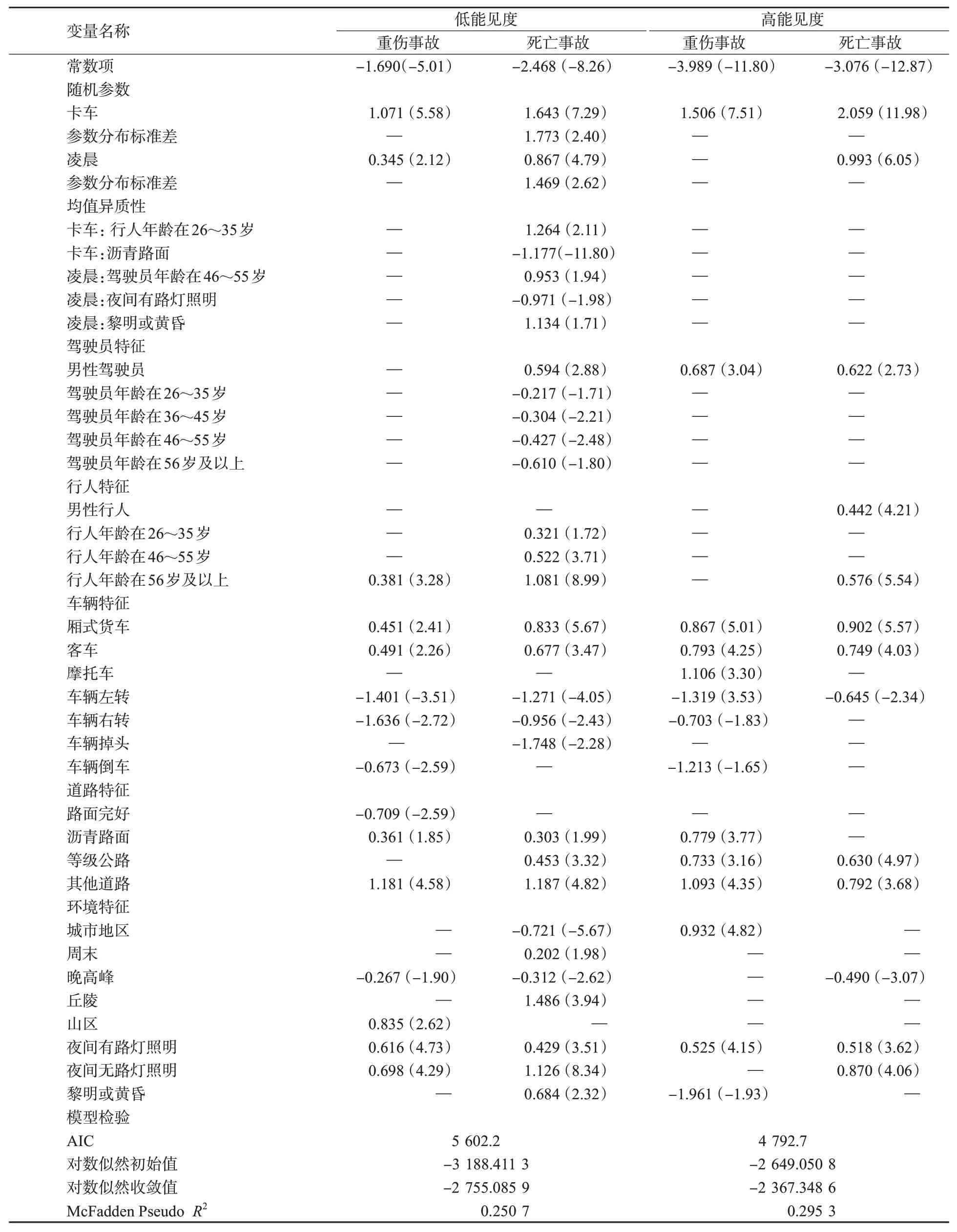
表2 参数估计结果Tab.2 Results of parameter estimation

3.2 均值异质性

与传统的随机参数Logit模型相比，考虑均值异质性的随机参数Logit模型能够捕获可能存在于随机参数均值中的个体异质性，进一步探索造成随机参数的可能因素。

由表2可知，行人年龄在26～35岁和沥青路面会影响变量“卡车”的随机参数均值。变量“卡车”的随机参数均值与行人年龄在26～35岁呈正相关，意味着卡车会增大事故中行人的致死概率，并且增加幅度在涉及到26～35岁的行人时会进一步增大。如图2（a）所示，在低能见度情况下的卡车事故中，25岁以下行人对于伤害严重程度为死亡的参数均值为1.643，当事故涉及到年龄在26～35岁的行人时，参数均值增大到了2.907（1.643+1.264=2.907）。变量沥青路面与“卡车”呈负相关，在低能见度情况下涉及卡车的事故会增加行人死亡的可能性，但是沥青路面能够减小这种增加的幅度。

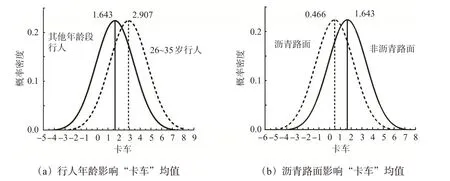
图2 “卡车”均值异质性参数分布Fig.2 Distribution of random parameters with heterogeneity in means for“truck”

变量“凌晨”的随机参数的均值具有异质性，并且与驾驶员年龄在46～55岁和黎明或黄昏呈正相关，在低能见度情况下的凌晨事故中，对于25岁以下驾驶员以及白天，其对于伤害严重程度为死亡的类别的参数均值均为0.867，然而对于46～55岁的驾驶员和黎明或黄昏，参数均值分别为1.820和2.001，见图3（a）～（b）。表明在低能见度情况下发生在凌晨的事故会增加行人死亡的可能性，并且增加的幅度对于涉及46～55岁的驾驶员和黎明或黄昏情况会进一步增加。但变量“凌晨”与夜间有路灯照明呈负相关，从图3（c）可见：在低能见度情况下发生于凌晨的事故中，对于白天，其对于死亡类别的参数均值为0.813，而在有路灯照明情况下，参数均值变为-0.104，这意味着在低能见度发生于凌晨的事故中，夜间有路灯照明能改变影响方向，使得行人在事故中无伤或受轻伤的概率增大。

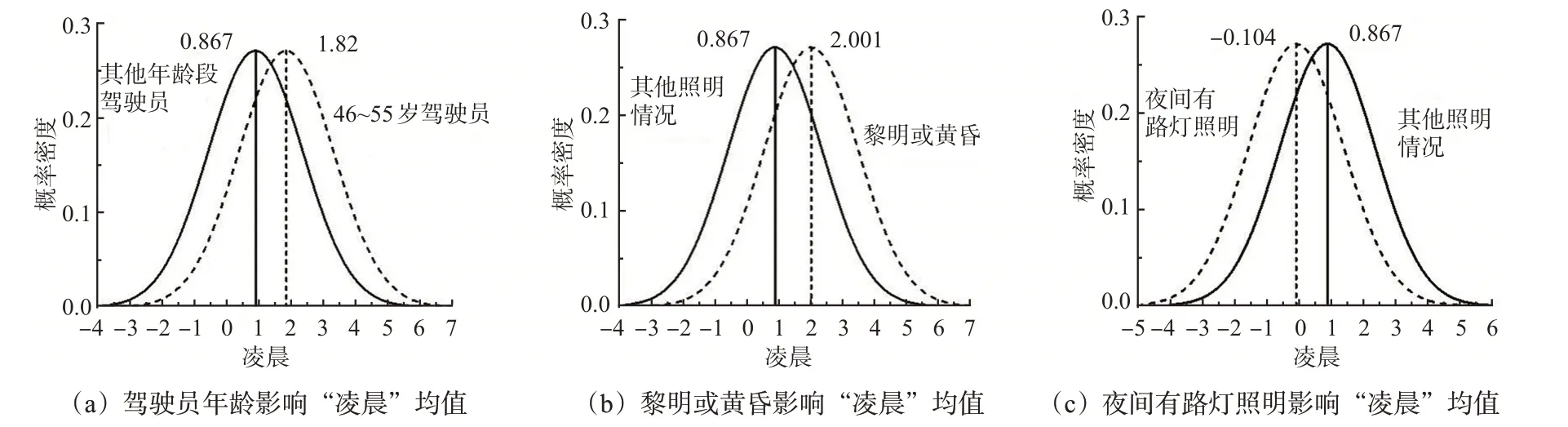
图3 “凌晨”均值异质性参数分布Fig.3 Distribution of random parameters with heterogeneity in means for“early morning hours”

4 事故影响因素分析

由表2可见：低能见度下的事故影响因素与高能见度情况下存在显著差异，因此接下来将结合弹性分析结果对低能见度情况下的事故影响因素进行分析，见表3。

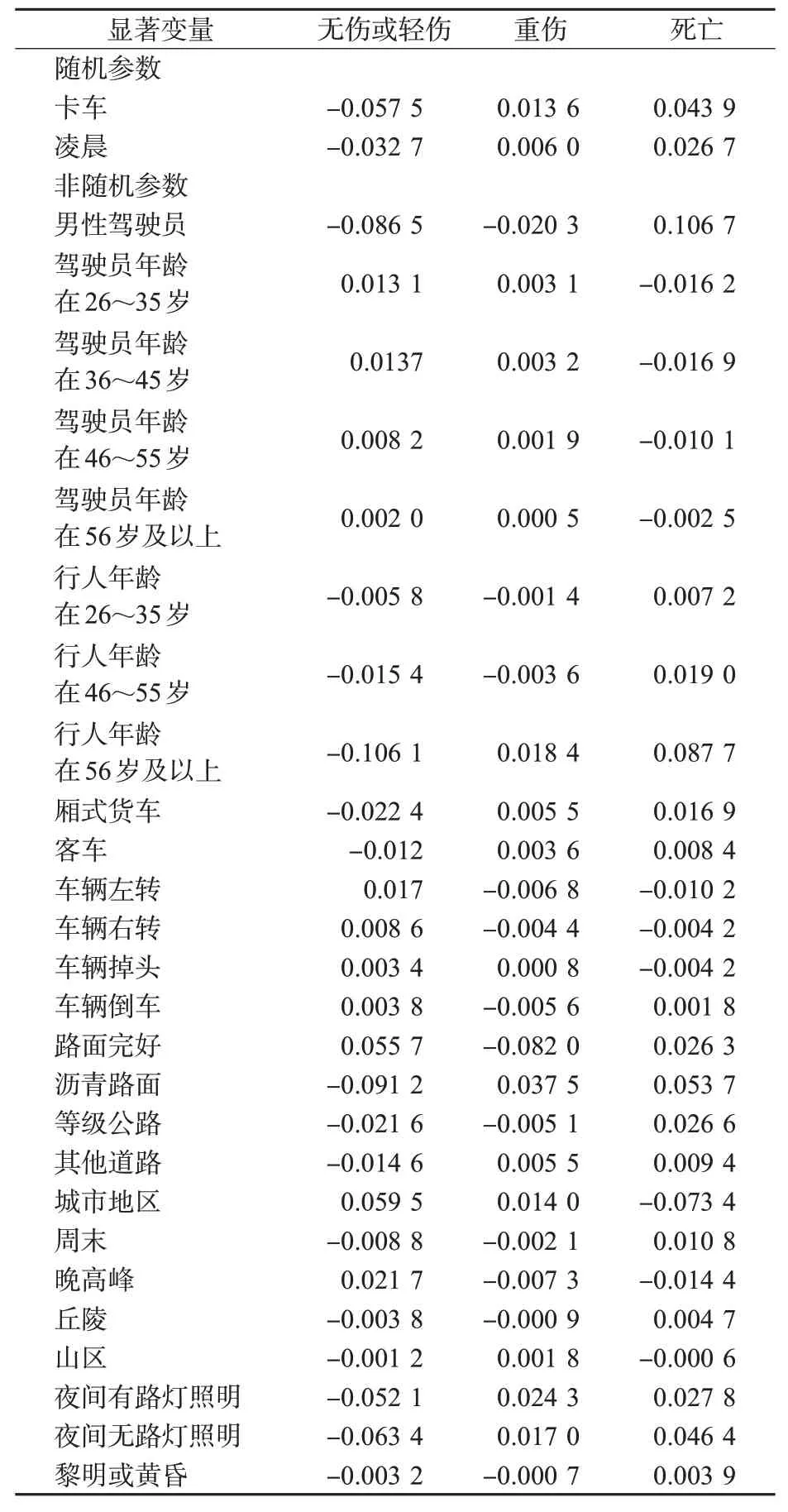
表3 弹性分析结果Tab.3 Results of elasticity analysis

4.1 驾驶员因素

在低能见度情况下，男性驾驶员对于死亡类别的弹性值为10.67%，意味着与女性相比，男性驾驶员在事故中造成行人死亡的概率要比女性驾驶员要更高，原因是男性驾驶员的驾驶行为更加冒进，行驶速度更高，进而导致增加发生死亡事故的概率。相较于25岁及以下的年轻驾驶员，较高年龄段的驾驶员对于死亡类别的弹性值均为负（分别为-1.62%，-1.69%，-1.01%，-0.25%），说明年龄越大，事故中行人遭受致命伤害的可能性越低，原因是驾驶员的年龄越大，驾驶经验就越丰富，遇到突发状况时采取的应对措施更好，而年轻驾驶员更容易采取冒险的驾驶行为。在高能见度结果中，驾驶员年龄对于行人伤害严重程度没有显著影响。

4.2 行人因素

低能见度结果中，发现行人年龄对于事故伤害严重程度有显著影响，与年轻人相比，年龄越大的行人在事故中死亡的概率越大（弹性值分别为0.72%，1.9%和8.77%），原因主要是行人年龄越大，其身体机能和健康状况也较差，面对突发事件的应变和反应能力也较弱，事故发生时来不及反应，进而导致遭受严重的事故伤害[20]。在高能见度结果中，男性行人受到致命伤害的概率要高于女性。

4.3 车辆因素

在低能见度情况下，厢式货车、卡车和客车均会显著增加事故中行人受到严重伤害的可能性（对应于死亡的弹性值分别为1.69%，4.39%和0.84%）。原因是中大型车辆的体积、质量较大，驾驶室的位置较高，驾驶人存在视野盲区，且车辆的惯性大、制动距离较长在行驶过程的操控性较差，遭遇紧急情况时不易采取应对措施，进而导致行人在事故中遭受重伤或死亡的可能性增大。与车辆直行相比，在车辆左转、右转、掉头和倒车时发生事故，行人无伤或仅受轻伤的概率分别增加了1.7%，0.86%，0.34%和0.38%。主要原因是车辆在转弯和倒车时，车速较低、车辆转弯半径较大、驾驶人比较警惕，观察较为充分，降低了事故中行人受到严重伤害的风险。

4.4 道路因素

在低能见度情况下，相较于破损的路面，完好的路面的弹性值为-0.082，意味着完好的路面能使行人受重伤的概率下降8.2%，此变量在高能见度情况下并不显著。沥青路面对于重伤和死亡类别的弹性值分别为27.5%和19.1%，说明在沥青路面上的事故会显著增加事故中行人受到严重伤害的风险。

与一般城市道路相比，等级公路会显著影响行人死亡的概率（对应于死亡的弹性值为2.66%），而发生在其他类型道路上的事故造成的事故后果更为严重（对应于重伤和死亡的弹性值分别为0.55%和0.94%）。

4.5 环境因素

根据表3，与农村地区相比，低能见度情况下发生在城市地区的事故造成行人死亡的可能性会下降7.34%，原因可能是在农村地区，交通标志标线和信号灯不如城市地区普遍，并且农村地区的交通流密度较低，交通信号控制设施缺乏，增大了车辆超速行驶的可能，致使行人死亡的概率上升。变量“周末”只在低能见度情况下会显著影响事故中行人死亡的概率，其弹性值为1.08%，意味着与周内相比，发生在周末的事故会使事故中行人死亡的概率增加3.9%。

低能见度情况下，变量“凌晨”具有随机参数特征，72.2%的行人在凌晨发生的事故中受到致命伤害的概率增加，其对于伤害严重程度为死亡的弹性值为2.67%，这主要是因为夜间光线昏暗，能见度低，驾驶人的感知风险的能力较低，面对突发情况，反应时间更长，故增加了其发生严重伤害的风险。与变量“凌晨”相反，“晚高峰”对应于重伤和死亡的弹性值均为负，意味着与其他时间相比，行人在发生在晚高峰的事故中受重伤或死亡的概率分别下降了-0.73%和-1.44%，潜在原因是在该时段光线较暗，驾驶员行车较为谨慎，并且晚高峰时交通较为拥堵，车速较慢，因此降低了行人受到严重伤害的概率。

地形对于低能见度事故中行人伤害严重程度也有显著影响，变量“丘陵”对于死亡类别的弹性值为1.7%，而变量“山区”对于重伤类别的弹性值为1.3%，说明相较于平原地形，发生在丘陵和山区地形的事故会增加行人受到严重伤害的概率。这主要是由于与上述地区相比，平原地区挡驾驶人视线的障碍物较少，驾驶人视野开阔，能对前方状况进行预判且在事故发生前有足够的时间采取合理的避险措施[21]。高能见度结果中地形对于行人伤害严重程度没有显著影响，因此需要重点关注低能见度情况下的非平原地区的行人安全。

低能见度情况下，“夜间有路灯照明”对于重伤和死亡类别的弹性值分别为2.43%和2.78%，“夜间无路灯照明”对于重伤和死亡类别的弹性值分别为1.7%和4.64%，原因是在上述情况下光线暗淡，能见度降低，驾驶员视距变短，在此条件下感知风险的能力会降低，遇到应对突发情况所需的反应时间需要更多的反应时间，增加了行人受到严重伤害的风险[22]。因此在夜间低能见度情况下，无论是否有路灯照明，驾驶员都应该谨慎低速驾驶，以保护道路交通参与者的安全。发生在凌晨或黄昏时分的事故中行人死亡的概率上升了0.39%。

5 结束语

为了分析在低能见度情况下与行人-机动车碰撞事故中行人伤害严重程度显著相关的因素，基于中国某市6 405起的行人-机动车碰撞数据，建立考虑均值异质性的随机参数Logit模型分析影响事故中行人伤害严重程度的因素，并与高能见度情况进行对比。得出以下主要结论。

1）低能见度情况下，考虑均值异质性的随机参数Logit模型的结果表明，变量“卡车”和“凌晨”具有服从正态分布的随机参数特征。

2）随机参数变量“卡车”和“凌晨”具有均值异质性，表现为涉及到卡车时，事故中26～35岁的行人遭受致命伤害的概率会增大，而在沥青路面上能够减小发生死亡事故的风险；当事故发生在凌晨时，46～55岁的驾驶员和黎明或黄昏会增大事故中行人死亡的可能性，而在夜间有路灯照明情况下发生死亡事故的几率降低。

3）研究发现不同能见度情况下，事故影响因素有非常明显的差异：高能见度情况下未发现具有异质性的影响因素；高能见度情况下，驾驶员年龄、路面情况、周末和地形对行人伤害严重程度影响并不显著，而男性行人和摩托车在低能见度情况下并未观测到会对事故严重程度产生显著影响。

研究结果可为制定不同能见度情况下的行人保护措施提供依据：①需要加强对于重型车辆的监管，在非沥青路段设置限速标志，限制车速并提高驾驶员警惕性，降低事故风险；②交通管理部门加强对于凌晨时分的道路管理，对于年龄偏大的驾驶员增加安全教育与培训，增设道路照明设施，降低事故严重程度；③改善非城市地区的道路基础设施建设，加强周末的交通管理，更多的关注非平原地区的行人安全等。