具比率依赖Holling Ⅲ型功能性反应的非自治捕食者-食饵系统的正周期解

马 超， 赵治涛

(黑龙江大学 数学科学学院, 哈尔滨 150080)

0 引 言

种群动力学是生态学与生物数学的一个重要分支,主要研究种群与种群、种群与环境之间的相互作用关系。捕食者与食饵之间的动态关系是种群动力学中最重要、最普遍的关系,在保护生物物种、维护生态平衡等方面具有重要应用。因此,捕食者-食饵模型一直受到国内外生态学家和数学家的关注,并且已经取得了很多具有实际应用价值的研究成果。

在对捕食者-食饵系统的研究中,功能性反应占有非常重要的地位,它表示单位时间内一个捕食者杀捕食饵的数量,刻画了在不同营养等级之间的生物转移量。针对不同的生物种群模型,分别建立了Holling型功能性反应、Hassell-Varley型功能性反应、Beddington-DeAngelis型功能性反应、比率依赖型功能性反应等,并得到了国内外生态学家与数学家广泛而深入的研究。捕食者的捕食能力,通常随食饵数量的变化而变化。当捕食者偏爱的食饵数量减少时,捕食者的捕获率会相应地减少,这种关系最早是被Leslie和Gower发现的,并据此建立了Leslie-Gower模型[1]。为了弥补捕食者偏爱食饵严重缺失的情况,学者们又建立了修正的Leslie-Gower模型[2]。对于Leslie-Gower模型以及相关的修正模型的研究,已经取得了许多有价值的研究成果[3-7]。近年来,尽管基于比率依赖型的捕食模型已经吸引了越来越多的学者关注[8-17],但是,对基于比率依赖Holling Ⅲ型功能性反应的捕食模型的研究成果还不够丰富。因此,研究具有比率依赖Holling Ⅲ型功能性反应的Leslie-Gower捕食模型不仅具有理论意义,更具有一定的实际应用价值。

然而,由于受到天气、食物供应、动物的交配习性等因素影响,种群的出生率、死亡率以及影响种群的其他重要因素会随时间发生相应的变化,于是,建立非自治捕食模型将会更加符合实际。基于此,本文将研究一类具比率依赖Holling Ⅲ型功能性反应的非自治捕食者-食饵系统：

(1)

式中：x(t)和y(t)分别表示在t时刻食饵种群和捕食者种群的密度；a(t),b(t),c(t),d(t),m(t),n(t)都是非负的连续函数。当系统参数是周期函数时,研究系统(1)的正周期解的存在性,并借助于数值模拟验证本文所得理论结果的有效性。

1 周期解的存在性

在本节中,将利用重合度的延拓定理与微分方程的比较定理,研究系统(1)的正周期解的存在性。为此,首先假设系统(1)中的所有参数关于时间t是以正数ω为周期的。为叙述方便,引入如下记号:

式中g是以正数ω为周期的连续实函数,即对任意的t∈,都有g(t+ω)=g(t)。

接下来,介绍重合度的延拓定理,也可参考文献[18]。

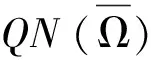
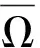
(i) 对于任意λ∈(0,1),Lz=λNz的任意解z均满足z∉∂Ω；

(ii) 对于任意z∈∂Ω∩kerL,有QNz≠0,并且其Brouwer度为：

deg{JQN,Ω∩kerL,0}≠0

为考虑系统(1)周期解的存在性,需要将问题放在重合度理论框架之下。为此,设

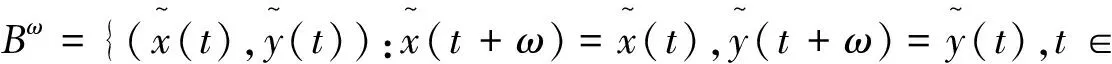
则Вω关于范数‖·‖构成一个Banach空间。再设

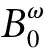
证明首先,系统(1)经过点(x(0),y(0))的解轨线可写为

令

则系统(1)变形为:

(2)

令X=Z=Вω,并定义

进而得到

为利用重合度延拓定理,还需构造一个适当的有界开集Ω,因此,定义如下的算子方程

即

(3)

(4)

根据式(3)和式(4),可知

(5)

(6)

根据式(6)和式(4)的第一个等式可得

因而得到：

于是

(7)

另一方面,根据式(6)和式(4)的第一个等式也可以得到：

(8)

整理即得

进而可以推得

(9)

因此,结合式(7)和式(9)得

另一方面,根据式(6)和式(4)的第二个等式,可得

(10)

整理可得：

于是得到：

(11)

同理,根据式(6)和式(4)的第二个等式,也可推得

(12)

整理即得

从而

(13)

于是,结合式(11)和式(13)可得：

显然,C1和C2的取值与参数λ无关。取C=C1+C2+C3,其中C3为充分大的正数,且满足

C3≥|A1|+|A2|+|A3|+|A4|

考虑代数方程

(14)

(15)

定义

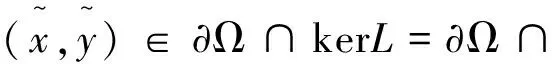
为了计算Brouwer度,考虑同伦映射

式中

deg(JQN,Ω∩KerL,0)=deg(QN,Ω∩KerL,0)=deg(G,Ω∩KerL,0)≠0,

则(x*(t),y*(t))是系统(1)的一个正ω周期解。 证毕。

2 数值模拟

通过数值模拟来验证上述所得的理论结果。令

a(t)=5.7[2+0.1sin(πt)],b(t)=3.15[0.045+0.01sin(πt)]

c(t)=0.2[1.5+5sin(πt)],d(t)=2[15+0.1cos(πt)]

m(t)=2[0.3+0.2cos(πt)],n(t)=0.07[0.35+0.3sin(πt)]

并且满足初始条件x(0)=70,y(0)=25,那么系统(1)存在一个周期为2的周期解,如图1所示。

图1 系统(1)的周期解Fig.1 Periodic solutions of system (1)